Sayı Kümeleri

Sayıları yazmak için kullanılan sembollere rakam adı verilir.
Rakamlar kümesi {0,1,2,3,4,5,6,7,8,9} dir.

SAYI KÜMELERİ

1. Sayma Sayıları ( $\displaystyle {{N}^{+}}$ ) : {1, 2, 3, … , n , …} kümesinin her bir elemanına sayma sayısı denir.

2. Doğal Sayılar (N): {0, 1, 2, 3, … , n , …} kümesinin her bir elemanına doğal sayı denir. $\displaystyle \mathbb{N}$ ile gösterilir.

3. Tam Sayılar (Z): {… , – n , … – 3, – 2, – 1, 0, 1, 2, 3, … , n , …} kümesinin her birelemanına tam sayı denir. $\displaystyle \mathbb{Z}$ şeklinde gösterilir.

Tam sayılar kümesi; negatif tam sayılar kümesi : $\displaystyle {{\mathbb{Z}}^{-}}$ şeklinde, pozitif tam sayılar kümesi : $\displaystyle {{\mathbb{Z}}^{+}}$ şeklinde gösterilir ve sıfırı eleman kabul eden: {0} kümenin birleşim kümesidir.
Buna göre, $\displaystyle \mathbb{Z}={{\mathbb{Z}}^{-}}\cup \left\{ 0 \right\}\cup {{\mathbb{Z}}^{+}}$ dır.

4. Rasyonel Sayılar (Q): a ve b birer tam sayı ve $\displaystyle b\ne 0$ olmak koşuluyla $\displaystyle \frac{a}{b}$ biçiminde yazılabilen sayılara rasyonel sayılar denir.

$\displaystyle \mathbb{Q}=\left\{ {\frac{a}{b};\text{ }a,\text{ }b\in \mathbb{Z},\text{ }b\ne 0} \right\}$ şeklinde gösterilir.

Not: Her tam sayı paydası 1 olan bir rasyonel sayıdır.

Not: İki rasyonel sayı arasında sonsuz sayıda rasyonel sayı bulunabilir.

Örnek: $\displaystyle \frac{2}{5},\text{ }\frac{{-7}}{3},\text{ }\frac{8}{4},\text{ 5}\text{, }-9$ birer rasyonel sayıdır.

5. İrrasyonel Sayılar (Q’): $\displaystyle \frac{a}{b}$ şeklinde yazılamayan yani rasyonel olmayan sayılara irrasyonel sayılar denir. Ondalıklı gösterimlerinde virgülden sonra belli bir kurala göre gitmezler. İrrasyonel sayılar kümesi $\displaystyle \mathbb{Q}'$ şeklinde gösterilir.

Örnek: $\displaystyle \sqrt{2},\text{ }\sqrt{5},\text{ }1+\sqrt{2},\text{ }-\sqrt[3]{{12}}\text{, }e=2,718...,\text{ }\pi =3,1415926...$ sayıları birer irrasyonel sayıdır.

Not: Bir sayı hem rasyonel hem de irrasyonel olamaz.

Not: $\displaystyle \sqrt{3},\text{ }\sqrt{5}$ gibi kökten çıkmayan sayılar irrasyoneldir.

6. Gerçek (Reel) Sayılar (R): Rasyonel sayılar kümesiyle irrasyonel sayılar kümesinin birleşimi olan kümeye reel gerçek (reel) sayılar kümesi denir.
$\displaystyle \mathbb{R}=\mathbb{Q}\cup \mathbb{Q}'$ şeklinde gösterilir.

Örnek: $\displaystyle -2,\text{ }\frac{3}{8},\text{ }\frac{\pi }{3},\text{ e}\text{, }\sqrt[3]{6},\text{ 5}$ birer gerçek sayıdır.

Örnek:

$\displaystyle -5,\text{ }-\sqrt{9},\text{ 2}\text{, }\frac{5}{3},\text{ }\sqrt{5},\text{ 0}\text{, 6}\text{, 6}\sqrt{3},\text{ 2}\text{,}\overline{\text{3}},\text{ }\pi$ sayılarından hangileri,

a) doğal sayıdır?

b) tam sayıdır?

c) rasyonel sayıdır?

d) irrasyonel sayıdır?

Çözüm İçin Tıklayınız

a) $\displaystyle \text{2}\text{,0}\text{,6}$ birer doğal sayıdır.

b) $\displaystyle -5,2,0,6$ birer tam sayıdır. Ayrıca $\displaystyle -\sqrt{9}$ da bir tam sayıdır. Çünkü $\displaystyle -3$ e eşittir.

c) $\displaystyle -5,\text{ }-\sqrt{9}\text{ },\text{ }2,\text{ }\frac{5}{3},\text{ }0,\text{ }6,\text{ 2}\text{,}\overline{\text{3}}$ birer rasyonel sayıdır.

d) $\displaystyle \sqrt{5},\text{ 6}\sqrt{3},\text{ }\pi$ birer irrasyonel sayıdır.

Sayı Kümelerininin Venn Şemasıyla Gösterimi

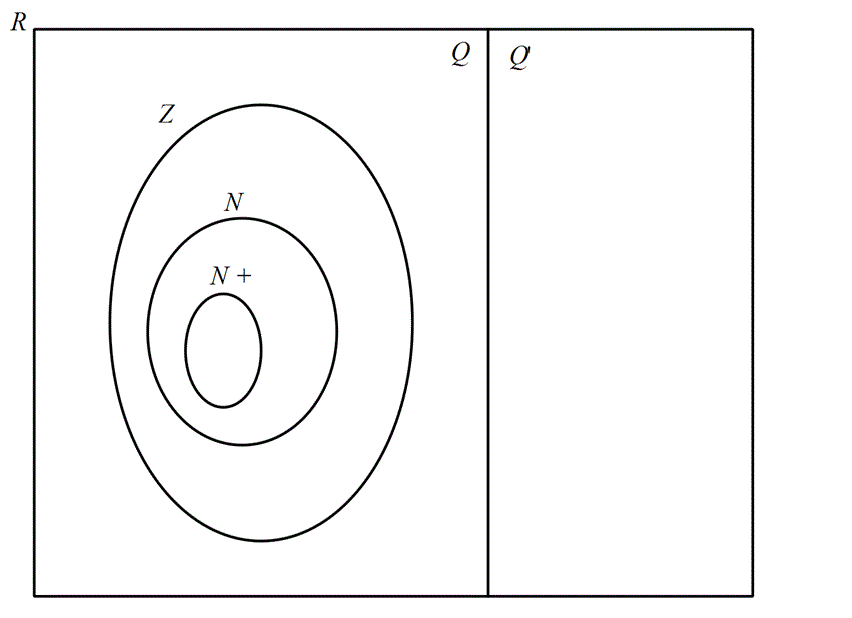
$\displaystyle {{N}^{+}}\subset N\subset Z\subset Q\subset R$ ve $\displaystyle Q'\subset R$ şeklinde kümeleri ifade edebiliriz. Ayrıca,

$\displaystyle Q\cap Q'=\varnothing$ ve $\displaystyle Q\cup Q'=R$ olduğunu görebiliriz.

Pergelle bir sayıyı sayı doğrusu üzerinde gösterme

Örnek: $\displaystyle \sqrt{2}$ sayısını sayı doğrusu üzerinde nasıl gösteririz?

İlk önce sayı doğrusu üzerinde dik kenarları 1’er birim olacak şekilde üçgen çizeriz. Bu üçgenin hipotenüsü $\displaystyle \sqrt{2}$ birimdir.

Yarıçap $\displaystyle \sqrt{2}$ olacak şekilde pergelle çember çizersek, bunun sayı doğrusunu kestiği pozitif nokta $\displaystyle \sqrt{2}$ dir.

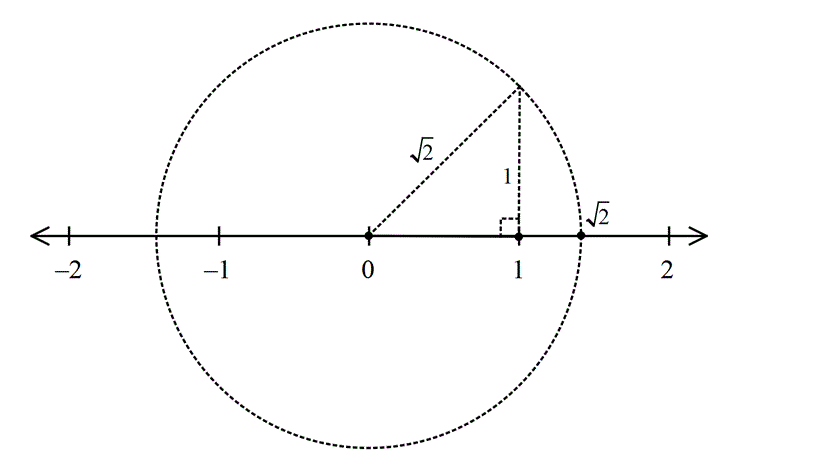
Gerçek Sayılarda Toplama İşleminin Özellikleri

1. Kapalılık özelliği: Her a, b ∈ R için a + b ∈ R dir. Gerçek sayılar kümesi toplama işlemine göre kapalıdır.

2. Değişme özelliği: Her a, b ∈ R için a + b = b + a olur. Gerçek sayılar kümesinde toplama işleminin değişme özelliği vardır.

3. Birleşme özelliği: Her a, b, c ∈ R için (a + b) + c = a + (b + c) olur. Gerçek sayılar kümesinde toplama işleminin birleşme özelliği vardır.

4. Etkisiz eleman: Her a ∈ R için a + 0 = 0 + a = a olur. Gerçek sayılar kümesinde 0, toplama işleminin etkisiz (birim) elemanıdır.

5. Ters eleman: Her a ∈ R için a + (– a) = (– a) + a = 0 olur. Gerçek sayılar kümesinde her elemanın toplama işlemine göre tersi vardır.

Örnek:

$\displaystyle (\sqrt{3}+4)+\sqrt{2}=\sqrt{3}+(\sqrt{2}+x)$ eşitliğindeki x’i toplama işleminin özelliklerini kullanarak bulalım.

Çözüm:

$\displaystyle \sqrt{3}+(4+\sqrt{2})=\sqrt{3}+(\sqrt{2}+x)$ Birleşme Özelliği

$\displaystyle \sqrt{3}+(\sqrt{2}+4)=\sqrt{3}+(\sqrt{2}+x)$ Değişme Özelliği

$\displaystyle \sqrt{3}+(-\sqrt{3})+(\sqrt{2}+4)=\sqrt{3}+(-\sqrt{3})+(\sqrt{2}+x)$ Ters Eleman Özelliği

$\displaystyle \sqrt{2}+(-\sqrt{2})+4=\sqrt{2}+(-\sqrt{2})+x$ Ters Eleman Özelliği

$\displaystyle x=4$ bulunur.

Gerçek Sayılarda Çarpma İşleminin Özellikleri

1. Kapalılık özelliği: Her a, b ∈ R için a · b ∈ R dir. Gerçek sayılar kümesi çarpma işlemine göre kapalıdır.

2. Değişme özelliği: Her a, b ∈ R için a · b = b · a olur. Gerçek sayılar kümesinde çarpma işleminin değişme özelliği vardır.

3. Birleşme özelliği: Her a, b, c ∈ R için (a · b) · c = a · (b · c) olur. Gerçek sayılar kümesinde çarpma işleminin birleşme özelliği vardır.
4. Etkisiz eleman: Her a ∈ R için a · 1 = 1 · a = a olur. Gerçek sayılar kümesinde çarpma işleminin etkisiz (birim) elemanı 1 dir.
5. Ters eleman: Her a ∈ R – {0} için $\displaystyle a\cdot \frac{1}{a}=\frac{1}{a}\cdot a=1$ olur. Gerçek sayılar kümesinde 0 hariç her elemanın çarpma işlemine göre tersi vardır.

6. Yutan eleman: Her a ∈ R için a · 0 = 0 · a = 0 olur. Gerçek sayılar kümesinde çarpma işleminin yutan elemanı 0 dır.

7. Dağılma özelliği: Her a, b, c ∈ R için a · (b + c) = a · b + a · c ve (b + c) · a = b · a + c · a dır. Gerçek sayılar kümesinde çarpma işleminin toplama işlemi üzerine soldan ve sağdan dağılma özelliği vardır.

Örnek:

2’nin toplama işlemine göre tersi ile 3’ün çarpmaya göre tersi çarpılırsa sonuç kaç olur?

Çözüm:

2 nin toplamaya göre tersi -2 dir.

3’ün çarpmaya göre tersi $\displaystyle \frac{1}{3}$ tür.

Bu ikisini çarparsak,

$\displaystyle -2\cdot \frac{1}{3}=-\frac{2}{3}$ buluruz.

Sayı Doğrusu

Gerçek sayılar kümesinin her elemanına sayı doğrusunda bir
nokta karşılık gelir. Gerçek sayılar kümesinin geometrik gösterimi sayı doğrusudur.

Örnek: $\displaystyle A(3),\text{ B(}-5\text{)}\text{, C(}\sqrt{2}\text{-1)}$ in sayı doğrusu üzerindeki yerleri aşağıdaki gibidir.

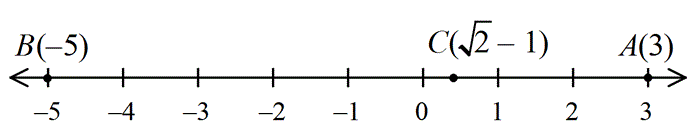
Koordinat Sistemi

Gerçek sayılarla elde edilen sıralı ikililer kümesinin her elemanına koordinat sistemi üzerinde bir nokta karşılık gelir.

R x R nin geometrik gösterimi koordinat sistemi olur.

Örnek:

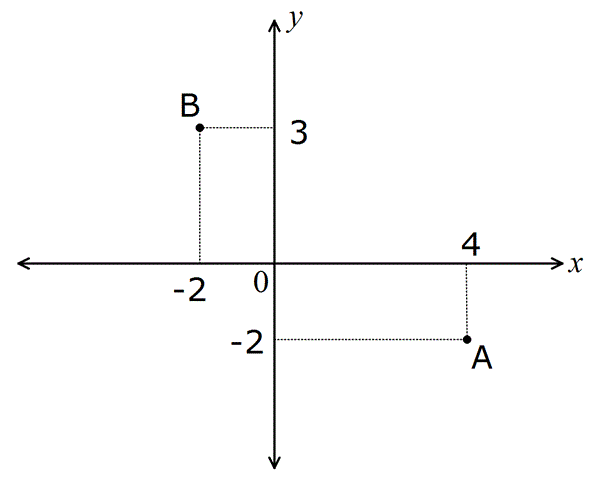
Yukarıdaki koordinat sisteminde A(a, b) ve B(c, d) noktaları verilmiştir. Buna göre, a.c-b.d işleminin sonucu kaçtır?

Çözüm:

A noktası (4, -2) noktasıdır.

B noktası ise (-2, 3) noktasıdır. Buna göre,

a.c-b.d=4.(-2)-(-2).3=-8+6=-2 dir.

Çözümlü Sorular veya Çıkmış Sorular için Tıklayın

Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)

Sayı Kümeleri

“Sayı Kümeleri” üzerine 2 yorum

Yorum yapın Cancel reply