Koşullu Önerme ve İki Yönlü Koşullu Önerme
p ile q önermelerinin ‘‘ise’’ bağlacı ile bağlanmasından oluşan bileşik önermeye koşullu önerme denir ve bu koşullu önerme ![]() biçiminde gösterilir.
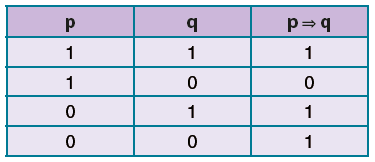
biçiminde gösterilir.![]() önermesi; p doğru, q yanlış iken yanlış diğer durumlarda doğrudur.
önermesi; p doğru, q yanlış iken yanlış diğer durumlarda doğrudur.
Örnek:
• p : ‘‘Batuhan evinde boşa yanan lambayı söndürür.”
• q : ‘‘Batuhan parasından tasarruf eder.’’
Yukarıda verilen önermelere göre ![]() önermesini yazalım.
önermesini yazalım.
![]() : ’’Batuhan evinde boşa yanan lambayı söndürür ise parasından tasarruf eder.’’
: ’’Batuhan evinde boşa yanan lambayı söndürür ise parasından tasarruf eder.’’
Örnek 19
![]() ve
ve ![]() olmak üzere aşağıdaki bileşik önermelerin doğruluk değerlerini bulunuz.
olmak üzere aşağıdaki bileşik önermelerin doğruluk değerlerini bulunuz.
![]()
Çözüm
![]()
![]()
![]()
(ise bağlacı sadece ![]() durumunda 0’a denktir. Diğer durumlarda hep 1 dir. )
durumunda 0’a denktir. Diğer durumlarda hep 1 dir. )
![]()
Çözüm
![]()
![]()
![]()
![]()
Çözüm
![]()
![]()
![]()
![]()
![]()
Çözüm
![]()
![]()
![]()
![]()
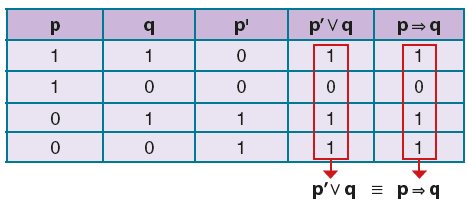
![]() önermesi
önermesi ![]() önermesine denktir.
önermesine denktir.
Örnek 20
![]() önermesinin değerini bulunuz.
önermesinin değerini bulunuz.
Çözüm
![]()
![]()
![]()
![]()
![]()
Not:
![]()
![]()
![]()
![]()
![]()
Örnek 21
Aşağıda verilen önermelerin en sade hâllerini bulunuz.
![]()
Çözüm
![]()
![]()
![]()
Çözüm
![]()
![]()
![]()
![]()
![]()
![]()
Çözüm
![]()
![]()
![]()
![]()
Örnek 22
![]() bileşik önermesinde p, q ve r önermelerinin doğruluk değerlerini
bileşik önermesinde p, q ve r önermelerinin doğruluk değerlerini
bulunuz.
Çözüm
“ve” bağlacının sonucu 1 olduğu için, iki önerme de 1 dir.
![]() ise
ise ![]() dır.
dır.
“ise” bağlacı sadece ![]() durumunda 0’a denktir. Bu sebeple,
durumunda 0’a denktir. Bu sebeple,
![]() ve
ve ![]() dır.
dır.
Ayrıca ![]() olduğundan
olduğundan ![]() dır.
dır.
![]()
Önermenin Karşıtı, Tersi ve Karşıt Tersi
• ![]() önermesinin karşıtı
önermesinin karşıtı ![]() dir.
dir.
• ![]() önermesinin tersi
önermesinin tersi ![]() dir.
dir.
• ![]() önermesinin karşıt tersi
önermesinin karşıt tersi ![]() olur.
olur.
Not:
Bir önermenin doğruluk değeri ile karşıt tersinin doğruluk değeri aynıdır.
![]()
Örnek 23
![]() önermesinin karşıt tersini bulunuz.
önermesinin karşıt tersini bulunuz.
Çözüm
![]() önermesinin karşt tersi
önermesinin karşt tersi
![]()
![]()
![]()
![]()
![]()
![]() dir.
dir.
Not:
![]() koşullu önermesinin doğruluk değeri 1 ise bu koşullu önermeye gerektirme denir.
koşullu önermesinin doğruluk değeri 1 ise bu koşullu önermeye gerektirme denir.
“ancak ve ancak” Bağlacı ile Kurulan Bileşik Önermeler
p ve q iki önerme olmak üzere ![]() ile
ile ![]() koşullu önermelerinin
koşullu önermelerinin ![]() bağlacı ile birbirine bağlanmasından oluşan
bağlacı ile birbirine bağlanmasından oluşan ![]() bileşik önermesine iki yönlü koşullu önerme denir.
bileşik önermesine iki yönlü koşullu önerme denir.
İki yönlü koşullu önerme ![]() şeklinde yazılır ve “p ancak ve ancak q” olarak okunur.
şeklinde yazılır ve “p ancak ve ancak q” olarak okunur.
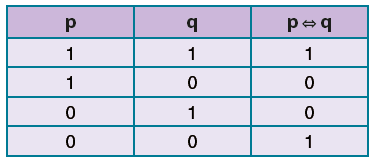
![]() iki yönlü koşullu önermesi p ile q nun doğruluk değerleri aynı iken doğru, farklı iken yanlıştır.
iki yönlü koşullu önermesi p ile q nun doğruluk değerleri aynı iken doğru, farklı iken yanlıştır.
Not:
![]()
Örnek 24
Aşağıdaki ifadelerin doğruluk değerlerini bulunuz.
![]()
Çözüm
![]()
![]()
![]()
Çözüm
![]()
![]()
![]()
![]()
Çözüm
![]()
![]()
![]()
Çözüm
![]()
![]()
![]()
“ancak ve ancak” Bağlacının Özellikleri
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Örnek 25
![]() önermesinin en sade halini bulunuz.
önermesinin en sade halini bulunuz.
Çözüm
![]()
![]()
Örnek 26
![]() önermesinin en sade halini bulunuz.
önermesinin en sade halini bulunuz.
Çözüm
![]()
![]()
Örnek 27
![]() önermesinin doğruluk değerini bulunuz.
önermesinin doğruluk değerini bulunuz.
Çözüm
![]()
![]()
![]()
![]()
![]()
![]()
Not:
![]() önermesinin doğruluk değeri 1 ise bu önermeye çift gerektirme denir.
önermesinin doğruluk değeri 1 ise bu önermeye çift gerektirme denir.
Alıştırma-1
p,q ve r önermelerine göre aşağıdakilerin doğruluk değerlerini bulunuz.
![]() ise,
ise,
![]()
Cevabı Gör
![]()
![]()
![]()
![]()
Cevabı Gör
![]()
![]()
![]()
![]()
Cevabı Gör
![]()
![]()
![]()
![]()
Cevabı Gör
![]()
![]()
![]()
![]()
Alıştırma-2
Aşağıdaki önermenin doğruluk değerlerini bulunuz.
![]() ise
ise ![]()
Cevabı Gör
“ise” bağlacında sadece ![]() a denktir.
a denktir.
![]()
![]() ise
ise
![]() dır. Ayrıca
dır. Ayrıca ![]() olmalı. Buna göre,
olmalı. Buna göre,
![]()
![]()
![]()
![]()
![]()
Alıştırma-3
Aşağıdaki önermenin en sade halini bulunuz.
![]()
Cevabı Gör
![]()
![]()
![]()
![]()
![]()
Alıştırma-4
Aşağıdaki önermenin en sade halini bulunuz.
![]()
Cevabı Gör
![]()
![]()
![]() dir.
dir.
Alıştırma-5
Aşağıdaki önermenin en sade halini bulunuz.
![]()
Cevabı Gör
![]()
![]()
![]()
![]()
![]()
![]()
Alıştırma-6
Aşağıdaki önermenin tersini, karşıtını ve karşıt tersini yazınız.
“Bayrak dalgalanırsa vatan düşmez.”
Tersi=?
Cevabı Gör
![]() “Bayrak dalgalanır.”
“Bayrak dalgalanır.”
![]() “Vatan düşmez.”
“Vatan düşmez.”
![]() nun tersi
nun tersi ![]() dür. O halde,
dür. O halde,
![]() : “Bayrak dalgalanmazsa vatan düşer.”
: “Bayrak dalgalanmazsa vatan düşer.”
Karşıtı=?
Cevabı Gör
![]() nun karşıtı
nun karşıtı ![]() dir. O halde,
dir. O halde,
![]() : “Vatan düşmezse bayrak dalgalanır.”
: “Vatan düşmezse bayrak dalgalanır.”
Karşıt Tersi=?
Cevabı Gör
![]() nun karşıtı
nun karşıtı ![]() dür. O halde,
dür. O halde,
![]() : “Vatan düşerse bayrak dalgalanmaz.”
: “Vatan düşerse bayrak dalgalanmaz.”
Alıştırma-7
Aşağıdaki önermenin en sade halini bulunuz.
![]()
Cevabı Gör
![]()
![]()
![]()
![]()
![]()



çoq iyi
eyw abi çok iyi anladım sağol çok iyi anlatmışsın hocadan daha iyisin yeminle 😀 kolay gelsin 10. sınıftada böle bekliyom
Özge bu notları çok beğendi. Ellerinize sağlık.
Hocam merhabalar yeni başlamış bir öğretmen olarak bilgilerinizden faydalanırken her seferinde Allah razı olsun diyorum işimi çok kolaylaştırıyor Teşekkür ederim böyle net anlatım ve bilgiler için .