Mantık Konu Anlatımı

2.sayfaya geçmek için tıklayınız.

De Morgan kuralları

p veya q nun değili: $\displaystyle (p\vee q)'\equiv p'\wedge q'$ dir.

p ve q nun değili: $\displaystyle (p\wedge q)'\equiv p'\vee q'$ dir.

Örnek 15

Aşağıdaki ifadelerin en sade halini bulunuz.

$\displaystyle (p'\wedge q)'\vee q$

Çözüm

$\displaystyle \equiv (p\vee q')\vee q\text{ (De Morgan)}$

$\displaystyle \equiv p\vee (q'\vee q)$

$\displaystyle \equiv p\vee 1$

$\displaystyle \equiv 1$

$\displaystyle (p\vee q')'\wedge q'$

Çözüm

$\displaystyle \equiv (p'\wedge q)\wedge q'$

$\displaystyle \equiv p'\wedge (q\wedge q')$

$\displaystyle \equiv p'\wedge 0$

$\displaystyle \equiv 0$

Örnek 16

Aşağıdaki ifadelerin en sade halini bulunuz.

$\displaystyle (p'\vee 0)'\wedge (q\wedge 1)'$

Çözüm

$\displaystyle \equiv (p\wedge 1)\wedge (q'\vee 0)\text{ (De Morgan)}$

$\displaystyle \equiv p\wedge q'$

$\displaystyle (p\vee q)\wedge (p\wedge q')'$

Çözüm

$\displaystyle \equiv (p\vee q)\wedge (p'\vee q)\text{ (De Morgan)}$

$\displaystyle \equiv (p\wedge p')\vee q$ (Dağılma özelliği)

$\displaystyle \equiv 0\vee q$

$\displaystyle \equiv q$

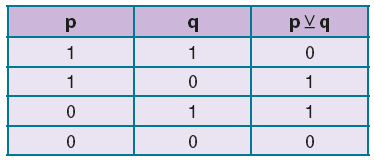
‘‘ya da ‘‘ Bağlacı

p ile q önermelerinin “ya da” bağlacı ile bağlanmasından oluşan bileşik önermeye, p ya da q bileşik önermesi denir ve önerme $\displaystyle p\text{ }\underline{\vee }\text{ }q$ biçiminde gösterilir.
$\displaystyle p\text{ }\underline{\vee }\text{ }q$ bileşik önermesi; p ile q önermelerinden yalnız biri doğru iken doğru, diğer durumlarda yanlıştır.

Örnek:

“Babası, Büşra’ya cep telefonu ya da bilgisayar aldı.” ifadesindeki olası durumlar:

Babası’nın Büşra’ya cep telefonu alıp bilgisayar almamış olması doğru,
Bilgisayar alıp cep telefonu almamış olması doğru,
Hem cep telefonu hem de bilgisayar almış olması yanlış,
Her ikisini almamış olması yanlış bir ifade belirtir.
(Yalnız birinin alındığı durumda ifadenin doğru olduğuna dikkat ediniz.)

Örnek 17

Aşağıdaki ifadelerin doğruluk değerlerini bulunuz.

$\displaystyle 1\text{ }\underline{\vee }\text{ (0 }\underline{\vee }\text{ 1)}$

Çözüm

$\displaystyle \equiv 1\text{ }\underline{\vee }\text{ }1$

$\displaystyle \equiv 0$

$\displaystyle (0'\text{ }\underline{\vee }\text{ 0) }\underline{\vee }\text{ }0'$

Çözüm

$\displaystyle \equiv (1\text{ }\underline{\vee }\text{ 0) }\underline{\vee }\text{ }1$

$\displaystyle \equiv 1\text{ }\underline{\vee }\text{ }1$

$\displaystyle \equiv 0$

$\displaystyle (1\text{ }\underline{\vee }\text{ 1 }\!\!'\!\!\text{ ) }\underline{\vee }\text{ (}0'\text{ }\underline{\vee }\text{ }1)$

Çözüm

$\displaystyle \equiv (1\text{ }\underline{\vee }\text{ 0) }\underline{\vee }\text{ (1 }\underline{\vee }\text{ }1)$

$\displaystyle \equiv 1\text{ }\underline{\vee }\text{ 0}$

$\displaystyle \equiv 1$

$\displaystyle (1'\text{ }\underline{\vee }\text{ 0) }\underline{\vee }\text{ 1}$

Çözüm

$\displaystyle \equiv (0\text{ }\underline{\vee }\text{ 0) }\underline{\vee }\text{ 1}$

$\displaystyle \equiv 0\text{ }\underline{\vee }\text{ 1}$

$\displaystyle \equiv 1$

‘‘ ya da’’ Bağlacı İle Kurulan Bileşik Önermelerin Özellikleri

1. Değişme Özelliği

$\displaystyle p\text{ }\underline{\vee }\text{ q }\equiv \text{ }q\text{ }\underline{\vee }\text{ p}$

2. Birleşme Özelliği

$\displaystyle (p\text{ }\underline{\vee }\text{ q) }\underline{\vee }\text{ r }\equiv p\text{ }\underline{\vee }\text{ (}q\text{ }\underline{\vee }\text{ r)}$

NOT

$\displaystyle p\text{ }\underline{\vee }\text{ p }\!\!'\!\!\text{ }\equiv \text{ 1}$

$\displaystyle p\text{ }\underline{\vee }\text{ p }\equiv \text{ 0}$

$\displaystyle p\text{ }\underline{\vee }\text{ 1 }\equiv \text{ p }\!\!'\!\!\text{ }$

$\displaystyle p\text{ }\underline{\vee }\text{ 0 }\equiv \text{ p}$

Örnek 18

Aşağıdaki ifadelerin en sade halini bulunuz.

$\displaystyle (p\text{ }\underline{\vee }\text{ p }\!\!'\!\!\text{ ) }\!\!'\!\!\text{ }\underline{\vee }\text{ q}$

Çözüm

$\displaystyle \equiv 1\text{ }\!\!'\!\!\text{ }\underline{\vee }\text{ q}$

$\displaystyle \equiv 0\text{ }\underline{\vee }\text{ q}$

$\displaystyle \equiv q$

$\displaystyle q'\text{ }\underline{\vee }\text{ }(1\text{ }\underline{\vee }\text{ }q)$

Çözüm

$\displaystyle \equiv q'\text{ }\underline{\vee }\text{ }q'$

$\displaystyle \equiv 0$

$\displaystyle (1\text{ }\underline{\vee }\text{ }q')\text{ }\vee \text{ }(0\text{ }\underline{\vee }\text{ 0})$

Çözüm

$\displaystyle \equiv q\text{ }\vee \text{ }0$

$\displaystyle \equiv q$

$\displaystyle (p\wedge p')\text{ }\underline{\vee }\text{ }(q\vee \text{q }\!\!'\!\!\text{ })$

Çözüm

$\displaystyle \equiv 0\text{ }\underline{\vee }\text{ 1}$

$\displaystyle \equiv 1$

Alıştırma-1
p,q ve r önermelerine göre aşağıdakilerin doğruluk değerlerini bulunuz.

p : ‘‘İki basamaklı en küçük tam sayı -99 dur.’’
q : ‘‘Camın ham maddelerinden biri kumdur.’’
r : ‘‘Bir asal sayının 2 katının 1 fazlası daima bir asal sayıdır.’’

$\displaystyle (p\vee q\text{ }\!\!'\!\!\text{ })\wedge r$

Cevabı Gör

p ve q doğru, r ise yanlış bir önermedir.

$\displaystyle p\equiv 1,\text{ q}\equiv 1,\text{ r}\equiv 0$ dır. Buna göre,

$\displaystyle (p\vee q\text{ }\!\!'\!\!\text{ })\wedge r$

$\displaystyle \equiv (1\vee 1\text{ }\!\!'\!\!\text{ })\wedge 0$

$\displaystyle \equiv (1\vee 0)\wedge 0$

$\displaystyle \equiv 1\wedge 0$

$\displaystyle \equiv 0$

$\displaystyle (p\wedge q)'\vee r$

Cevabı Gör

$\displaystyle p\equiv 1,\text{ q}\equiv 1,\text{ r}\equiv 0$ idi. Buna göre,

$\displaystyle (p\wedge q)'\vee r$

$\displaystyle \equiv (1\wedge 1)'\vee 0$

$\displaystyle \equiv 1\vee 0$

$\displaystyle \equiv 1$

$\displaystyle (p'\vee r)\vee (p\wedge q')'$

Cevabı Gör

$\displaystyle p\equiv 1,\text{ q}\equiv 1,\text{ r}\equiv 0$ idi. Buna göre,

$\displaystyle (p'\vee r)\vee (p\wedge q')'$

$\displaystyle \equiv (1'\vee 0)\vee (1\wedge 1')'$

$\displaystyle \equiv (0\vee 0)\vee (1\wedge 0)'$

$\displaystyle \equiv 0\vee 0'$

$\displaystyle \equiv 0\vee 1$

$\displaystyle \equiv 1$

$\displaystyle p\wedge (q\vee r')$

Cevabı Gör

$\displaystyle p\equiv 1,\text{ q}\equiv 1,\text{ r}\equiv 0$ idi. Buna göre,

$\displaystyle p\wedge (q\vee r')$

$\displaystyle \equiv 1\wedge (1\vee 0')$

$\displaystyle \equiv 1\wedge (1\vee 1)$

$\displaystyle \equiv 1\wedge 1$

$\displaystyle \equiv 1$

Alıştırma-2
Aşağıdaki ifadelerin doğruluk değerlerini bulunuz.

$\displaystyle (1\vee 0)\wedge 1$

Cevabı Gör

$\displaystyle \equiv 1\wedge 1$

$\displaystyle \equiv 1$

$\displaystyle (0\wedge 1)\vee (1\vee 0)'$

Cevabı Gör

$\displaystyle \equiv 0\vee 1'$

$\displaystyle \equiv 0\vee 0$

$\displaystyle \equiv 0$

$\displaystyle (1'\wedge 0)\vee (0\vee 1)$

Cevabı Gör

$\displaystyle \equiv (0\wedge 0)\vee 1$

$\displaystyle \equiv 0\vee 1$

$\displaystyle \equiv 1$

$\displaystyle (1\wedge ((1\wedge 1)\wedge 1))\wedge 1'$

Cevabı Gör

$\displaystyle \equiv \underbrace{{(1\wedge ((1\wedge 1)\wedge 1))}}_{1}\wedge 1'$

$\displaystyle \equiv 1\wedge 1'$

$\displaystyle \equiv 0$

Alıştırma-3
Aşağıdaki denklikler doğru mu, yanlış mı?

$\displaystyle p'\vee p\equiv 1$

$\displaystyle (p\wedge q')'\equiv p'\vee q$

$\displaystyle p\wedge (q\vee r)\equiv (p\vee q)\wedge (p\vee r)$

Açıklama

$\displaystyle \equiv (p\wedge q)\vee (p\wedge r)$ olmalıydı.

$\displaystyle p\wedge 1\equiv 1$

Açıklama

$\displaystyle p\wedge 1\equiv p$ dir.

Alıştırma-4
Aşağıdaki önermelerin en sade halini bulunuz.

$\displaystyle p\vee (p\wedge q)'$

Cevabı Gör

$\displaystyle \equiv p\vee (p'\vee q')$

$\displaystyle \equiv (p\vee p')\vee q'$

$\displaystyle \equiv 1\vee q'$

$\displaystyle \equiv 1$

$\displaystyle (p\vee q')'\wedge p$

Cevabı Gör

$\displaystyle \equiv (p'\wedge q)\wedge p$

$\displaystyle \equiv (p'\wedge p)\wedge q$

$\displaystyle \equiv 0\wedge q$

$\displaystyle \equiv 0$

$\displaystyle (p\vee q')\wedge (p'\wedge q)'$

Cevabı Gör

$\displaystyle \equiv (p\vee q')\wedge (p\vee q')$

$\displaystyle \equiv p\vee (q'\wedge q')$

$\displaystyle \equiv p\vee q'$

$\displaystyle (p\vee q')'\vee (p'\wedge q')$

Cevabı Gör

$\displaystyle \equiv (p'\wedge q)\vee (p'\wedge q')$

$\displaystyle \equiv p'\wedge (q\vee q')$

$\displaystyle \equiv p'\wedge 1$

$\displaystyle \equiv p'$

Alıştırma-5
Aşağıdaki denkliğe göre p, q ve r nin doğruluk değerini bulunuz.

$\displaystyle (p\vee q')'\wedge (q\wedge r)\equiv 1$

Cevabı Gör

“ve” bağlacında sonuç 1 ise, iki ifadenin de doğruluk değeri 1 dir.

$\displaystyle \underbrace{{(p\vee q')'}}_{1}\wedge \underbrace{{(q\wedge r)}}_{1}\equiv 1$

$\displaystyle q\wedge r\equiv 1\text{ ise hem q}\equiv \text{1}\text{, hem de r}\equiv \text{1 dir}\text{.}$

$\displaystyle (\underbrace{{p\vee q'}}_{0})'\equiv 1$ ise

$\displaystyle p\vee q'\equiv 0\text{ }$ dır.

$\displaystyle p\equiv 0$ olmalıdır. Çünkü “veya” bağlacının sonucunun 0 olması için iki ifadenin de 0 olması gerekir.

$\displaystyle p\equiv 0\text{ }\text{, q}\equiv \text{1 }\text{, r}\equiv \text{1 }$

Alıştırma-6
Aşağıdaki ifadelerin en sade halini bulunuz.

$\displaystyle (p\wedge 0)\vee (p\vee 1)$

Cevabı Gör

$\displaystyle \equiv 0\vee 1$

$\displaystyle \equiv 1$

$\displaystyle (p\vee 0)\wedge (p'\wedge 1)$

Cevabı Gör

$\displaystyle \equiv p\wedge p'$

$\displaystyle \equiv 0$

Alıştırma-7
“ve”, “veya”, “ya da” bağlacının günlük hayatta kullanımı

19 Mayıs Lisesinde görev yapan Müdür Yardımcısı Selin Hanım, nöbetçi öğrenciyi çağırarak ona 9-C sınıfından Kemal veya Yağmur’un, odasına gelmesini söylemiştir. Nöbetçi öğrenci 9-C sınıfına girerken çağrılan iki öğrenci için arada kullanılan “ veya” bağlacını unutmuştur. Buna göre

Nöbetçi öğrenci bağlacı “ve” olarak hatırlarsa hangi olası durumların gerçekleşeceğini bulunuz.

Cevabı Gör

Kemal ve Yağmur, ikisi birden gidecektir.

Nöbetçi öğrenci bağlacı “ya da” olarak hatırlarsa hangi olası durumların gerçekleşeceğini bulunuz.

Cevabı Gör

Kemal ya da Yağmur’dan sadece biri gidecektir.

Nöbetçi öğrenci Selin Hanım’ın söylediğini doğru hatırlarsa hangi olası durumların gerçekleşeceğini bulunuz.

Cevabı Gör

Kemal veya Yağmur’dan biri gidebilir veya; ikisi de gidebilir. Ancak hiç kimse gitmezse hatalı olur.

Alıştırma-8
Aşağıdaki önermenin doğruluk değerini bulunuz. (ya da bağlacı)

$\displaystyle (1\text{ }\underline{\vee }\text{ 1 }\!\!'\!\!\text{ })\vee (0\text{ }\underline{\vee }\text{ 0 }\!\!'\!\!\text{ })$

Cevabı Gör

“ya da” bağlacında sonuç,

iki önerme farklı iken 1, aynı iken 0 olur.

$\displaystyle \equiv (1\text{ }\underline{\vee }\text{ 0})\vee (0\text{ }\underline{\vee }\text{ 1})$

$\displaystyle \equiv 1\vee 1$

$\displaystyle \equiv 1$

Alıştırma-9
Aşağıdaki önermenin en sade halini bulunuz.

$\displaystyle (p'\vee q\text{ }\!\!'\!\!\text{ })\text{ }\underline{\vee }\text{ }(p\wedge q)$

Cevabı Gör

$\displaystyle (p'\vee q\text{ }\!\!'\!\!\text{ })$ ifadesi De Morgan’a göre, $\displaystyle (p\wedge q)'$ önermesine denktir. Bu sebeple sorudaki önermeyi

$\displaystyle (p\wedge q)'\text{ }\underline{\vee }\text{ }(p\wedge q)$ olarak yazabiliriz.

İki parantez arasında “ya da” bağlacı var ve bu parantezler birbirlerinin tersi. Yani birisi 1 iken diğeri 0, birisi 0 iken diğeri 1 . Bu durum “ya da” bağlacında her zaman 1 sonucunu verir. Dolayısıyla cevap 1 olur.

$\displaystyle (p\wedge q)'\text{ }\underline{\vee }\text{ }(p\wedge q)\text{ }\left( {p\wedge q=r\text{ olsun}} \right)$

$\displaystyle \equiv r'\text{ }\underline{\vee }\text{ }r$

$\displaystyle \equiv 1\text{ olur}\text{.}$

4.sayfaya geçmek için tıklayınız.

Sayfalar: 1 2 3 4 5 6

“Mantık” üzerine 4 yorum

isimsiz

24 Ekim 2020 11:39 | Cevapla

çoq iyi
mehmet ali

8 Kasım 2020 18:36 | Cevapla

eyw abi çok iyi anladım sağol çok iyi anlatmışsın hocadan daha iyisin yeminle 😀 kolay gelsin 10. sınıftada böle bekliyom
Taylan

1 Temmuz 2021 19:56 | Cevapla

Özge bu notları çok beğendi. Ellerinize sağlık.
tu

6 Eylül 2021 23:22 | Cevapla

Hocam merhabalar yeni başlamış bir öğretmen olarak bilgilerinizden faydalanırken her seferinde Allah razı olsun diyorum işimi çok kolaylaştırıyor Teşekkür ederim böyle net anlatım ve bilgiler için .

“Mantık” üzerine 4 yorum

Yorum yapın Cancel reply