Bileşik Önermeler
İki veya daha fazla önermenin ‘‘ve’’, ‘‘veya’’, ‘‘ya da’’, ‘‘ise’’, ‘‘ancak ve ancak’’ gibi bağlaçlarla birbirine bağlanmasıyla elde edilen yeni önermeye bileşik önerme denir.
‘‘ve’’ Bağlacı ile Kurulan Bileşik Önermeler
p ile q önermelerinin ‘‘ve’’ bağlacı ile bağlanmasından oluşan bileşik önermeye, p ve q bileşik önermesi denir ve bu önerme p Λ q biçiminde gösterilir.
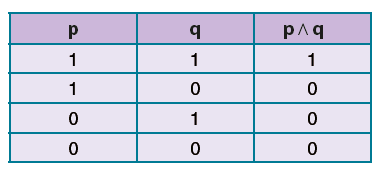
p Λ q bileşik önermesinin doğruluk değeri; p ile q önermelerinin her ikisi de doğru iken doğru, diğer durumlarında ise yanlıştır.
p ve q önermeleri için p Λ q önermesinin doğruluk tablosu aşağıdaki gibidir.
Örnek 8
![]()
![]()
Önermeleri için ![]() önermesini yazıp önermenin doğruluk değerini bulunuz.
önermesini yazıp önermenin doğruluk değerini bulunuz.
Çözüm
![]() şeklinde yazılır.
şeklinde yazılır.
![]() ve
ve ![]() olduğundan
olduğundan ![]() dır.
dır.
Örnek 9
Aşağıdaki ifadelerin doğruluk değerlerini bulunuz.
![]()
Çözüm
![]()
![]()
Çözüm
![]()
![]()
Çözüm
![]()
“ve’’ Bağlacı ile Kurulan Bileşik Önermelerin Özellikleri
1. Tek Kuvvet Özelliği
Her p önermesi için ![]() dir.
dir.
2. Değişme Özelliği
Her p, q önermesi için ![]() dir.
dir.
3. Birleşme Özelliği
Her p, q, r önermesi için ![]() dir.
dir.
Not:
![]()
![]()
![]()
Örnek 10
Aşağıdaki ifadelerin en sade halini yazınız.
![]() =?
=?
Çözüm
![]()
![]() =?
=?
Çözüm
![]()
Örnek 11
Aşağıdaki önermelerin doğruluk değerlerini bulunuz.
![]() =?
=?
Çözüm
![]()
![]() =?
=?
Çözüm
![]()
![]() =?
=?
Çözüm
![]()
![]() =?
=?
Çözüm
![]()
‘‘veya’’ Bağlacı ile Oluşan Bileşik Önermeler
p ile q önermelerinin “veya” bağlacı ile bağlanmasından oluşan bileşik önermeye, p veya q bileşik önermesi denir ve önerme ![]() biçiminde gösterilir.
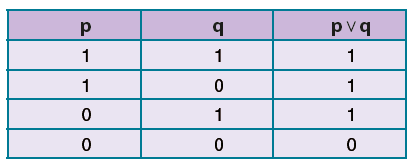
biçiminde gösterilir.![]() bileşik önermesi; p ile q önermelerinden en az biri doğru iken doğru, her ikisi de yanlış iken yanlıştır.
bileşik önermesi; p ile q önermelerinden en az biri doğru iken doğru, her ikisi de yanlış iken yanlıştır.
p ve q önermeleri için ![]() önermesinin doğruluk tablosu aşağıdaki gibidir.
önermesinin doğruluk tablosu aşağıdaki gibidir.
Not:
![]()
![]()
![]()
Örnek 11
Aşağıdaki ifadelerin doğruluk değerlerini bulunuz.
![]() =?
=?
Çözüm
![]()
![]() =?
=?
Çözüm
![]()
![]()
Çözüm
![]()
![]()
Çözüm
![]()
“veya’’ Bağlacı ile Kurulan Bileşik Önermelerin Özellikleri
1. Tek Kuvvet Özelliği
Her p önermesi için ![]() dir.
dir.
2. Değişme Özelliği
Her p, q önermeleri için ![]() dir.
dir.
3. Birleşme Özelliği
Her p, q, r önermesi için ![]() dir.
dir.
Örnek 12
Aşağıdaki ifadelerin doğruluk değerlerini bulunuz.
![]()
Çözüm
![]()
![]()
Çözüm
![]()
![]()
Çözüm
Hepsi “veya” bağlacı ile birleştirildiği için önermeleri istediğimiz gibi yer değiştirebiliriz.
![]()
![]()
Çözüm
![]()
Örnek 13
![]() için aşağıdaki ifadelerin doğruluk değerlerini bulunuz.
için aşağıdaki ifadelerin doğruluk değerlerini bulunuz.
![]()
Çözüm
![]()
![]()
Çözüm
![]()
![]()
Çözüm
![]()
![]()
Çözüm
![]()
Dağılma Özelliği
1. “ve” nin “veya” üzerine soldan dağılma özelliği
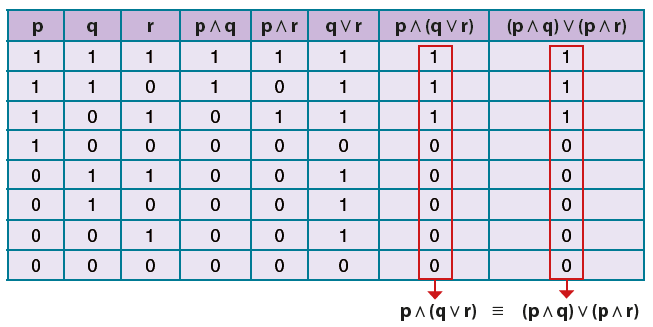
![]() dir.
dir.
Bunu doğruluk tablosu ile gösterelim.
“ve” nin “veya” üzerine sağdan dağılma özelliği
![]() dir.
dir.
2.“veya” nın “ve” üzerine soldan dağılma özelliği
![]() dir.
dir.
“veya” nın “ve” üzerine sağdan dağılma özelliği
![]() dir.
dir.
Örnek 14
Aşağıdaki ifadelerin en sade halini bulunuz.
![]()
Çözüm
![]()
![]()
![]()
![]()
Çözüm
![]()
![]()
![]()


çoq iyi
eyw abi çok iyi anladım sağol çok iyi anlatmışsın hocadan daha iyisin yeminle 😀 kolay gelsin 10. sınıftada böle bekliyom
Özge bu notları çok beğendi. Ellerinize sağlık.
Hocam merhabalar yeni başlamış bir öğretmen olarak bilgilerinizden faydalanırken her seferinde Allah razı olsun diyorum işimi çok kolaylaştırıyor Teşekkür ederim böyle net anlatım ve bilgiler için .