Mantık

Konu ile ilgili Çözümlü Soruları Görmek için Tıkla

Önerme

Doğru ya da yanlış kesin bir hüküm (yargı) bildiren ifadelere önerme adı verilir. Matematikte önermeler genellikle p, q, r, s gibi küçük harflerle gösterilir.


Örnek 1 için Tıklayınız.

Aşağıdaki ifadelerden hangilerinin bir önerme olduğunu bulunuz.

a) Bir ay otuz iki gündür.
b) Selimiye Camii Edirne’dedir.
c) Ödevini yaptın mı?
d) İyi akşamlar!
e) 1001 bir asal sayıdır.

 

Çözüm için Tıklayınız.

a, b ve e maddelerinde verilen ifadeler doğru ya da yanlış kesin bir hüküm bildirdiğinden birer önermedir. c ve d maddelerinde verilen ifadeler bir hüküm bildirmediğinden önerme değillerdir.

Bir önermenin doğru ya da yanlış olmasına, o önermenin doğruluk değeri denir.
Bir önerme doğru ise doğruluk değeri D veya 1 ile yanlış ise Y veya 0 ile gösterilir.
Bir p önermesi doğru bir önerme ise “p≡1“ , yanlış bir önerme ise “p≡0” şeklinde gösterilir ve “p önermesi 1 e denktir. ” ya da “ p önermesi 0 a denktir. ” şeklinde okunur.

Örnek 2 için Tıklayınız.

Aşağıdaki önermelerin doğruluk değerlerini bulunuz.
• p : ‘‘7 tek sayıdır.’’
• q : ‘‘İki basamaklı en büyük doğal sayı 99 dur.’’
• r : ‘‘24 > 42 dir.’’
• s : ‘‘Üçgenin iç açılarının ölçüleri toplamı 360 derecedir.’’
• t : ‘‘En küçük doğal sayı 0 dır.’’

 

Çözüm için Tıklayınız.

• “7 tek sayıdır.’’ hükmü doğru olduğundan p önermesinin doğruluk değeri 1 dir. p ≡ 1 olarak gösterilir.
• ‘‘İki basamaklı en büyük doğal sayı 99 dur.’’ hükmü doğru olduğundan q önermesinin doğruluk değeri 1 dir. q≡1 olarak gösterilir.
• 24 = 42 olduğundan r önermesi yanlış hüküm belirtir. r önermesinin doğruluk değeri 0 dır. r≡0 olarak gösterilir.
• Üçgenin iç açılarının ölçüleri toplamı 180 derece olduğundan s önermesi yanlış hüküm belirtir. s önermesinin doğruluk değeri 0 dır. s≡0 olarak gösterilir.
• ‘‘En küçük doğal sayı 0 dır.’’ hükmü doğru olduğundan t önermesinin doğruluk değeri 1 dir. t≡1 olarak gösterilir.

Doğruluk değerleri aynı olan iki önermeye denk önermeler denir. p önermesi q önermesine denk ise p≡q, p önermesi q önermesine denk değil ise p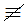q ile gösterilir.

Örnek 3 için Tıklayınız.

Aşağıda verilen önermelerden birbirine denk olanları bulunuz.
• p : ’’5 – 3 =3 – 5 tir.’’
• q : “Dünya Güneş’ten büyüktür.’’
• r : ’’-7 tam sayıdır.’’
• s : ’’ En büyük asal rakam 7 dir.’’

 

Çözüm için Tıklayınız.

p ve q önermeleri yanlış olduğundan doğruluk değerleri 0 dır. Dolayısıyla p ve q önermeleri denk önermelerdir ve p ≡ q olarak gösterilir.
r ve s önermeleri doğru olduğundan doğruluk değerleri 1 dir. Dolayısıyla r ve s  önermeleri denk önermelerdir ve r ≡ s olarak gösterilir.

Önermelerin doğruluk değerlerinin gösterildiği tabloya doğruluk tablosu denir.

p önermesinin doğruluk tablosunu oluşturalım.

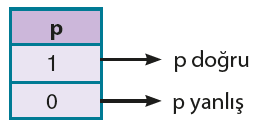
p ve q önermeleri için doğruluk tablosu oluşturalım.

p önermesinin 2, q önermesinin 2 farklı doğruluk değeri olduğundan p ve q önermelerinin 2 . 2 =\displaystyle {{2}^{2}} =4 farklı doğruluk durumu vardır.

Örnek 4 için Tıklayınız.

p, q ve r önermeleri için doğruluk tablosu oluşturunuz.

Çözüm için Tıklayınız.

Her önermenin 2 farklı doğruluk değeri olduğundan verilen üç önerme için 2 . 2 . 2 =\displaystyle {{2}^{3}} =8 farklı doğruluk durumu vardır. Önermelerin doğruluk tablosu aşağıdaki gibidir.

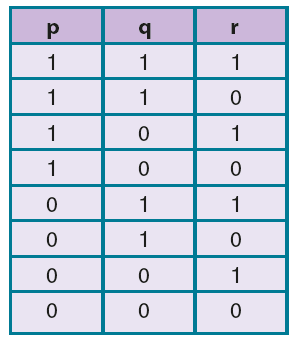
n farklı önermenin birbirine göre 2n tane doğruluk durumu vardır.

Örnek 5 için Tıklayınız.

5 farklı önermenin birbirine göre kaç farklı doğruluk durumu olduğunu bulunuz.

Çözüm için Tıklayınız.

5 farklı önermenin 25 =32 farklı doğruluk durumu vardır.

Bir önermenin hükmünün değiştirilip yerine olumsuzunun kullanılması ile elde edilen önermeye ilk önermenin değili (olumsuzu) denir.

p önermesinin değili p’ veya ~p ile gösterilir.
p önermesi doğru ise doğruluk değeri 1 dir ve p’ önermesinin doğruluk değeri 0 dır. p ≡ 1 ise p’ ≡ 0 ile gösterilir.
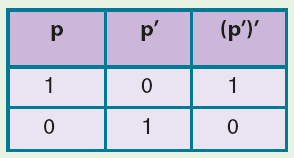
Bir önermenin değilinin değili önermenin kendisine denktir. [(p’)’ ≡ p]
Bu özelliğin doğruluk tablosu aşağıdaki gibidir.

Örnek 6

Aşağıda verilen önermelerin değilini bulunuz.
a) p : “Antalya ili Akdeniz Bölgesi’ndedir.’’
b) q : “Bir hafta 6 gün değildir.’’
c) r : “2 sayısı 10 dan küçüktür.’’

Çözüm için Tıklayınız.

a) p’ : “Antalya ili Akdeniz Bölgesi’nde değildir.’’
b) q’ : “Bir hafta 6 gündür.’’
c) r’ : “2 sayısı 10 dan büyük veya 10 a eşittir.’’

Örnek 7

Aşağıda verilen önermelerin değilini bulunuz.
a) p : ”-6 + 11=5 tir.”
b) q’ : ”-3 > 6 dır.”
c) s : ’’3≤2 dir.’’

Çözüm için Tıklayınız.

a) p’ : ”-6 + 11≠ 5 tir.”
b) q : ”-3 ≤ 6 dır.”
c) s’ : ’’3 > 2 dir.’’

Alıştırma-1
Hangileri önermedir, hangileri değildir?

Birbirinden farklı en küçük üç asal sayının toplamı 10 dur. (………………..)

Cevabı Gör

Önermedir.

Türkiye Cumhuriyeti Asya kıtasındadır. (………………..)

Cevabı Gör

Önermedir.

Fatih bu okulda mı? (………………..)

Cevabı Gör

Önerme Değildir.

Ay Dünya’nın uydusudur. (………………..)

Cevabı Gör

Önermedir.

Bugün hava güzel mi? (………………..)

Cevabı Gör

Önerme Değildir.

Alıştırma-2
Aşağıdaki önermelerin doğruluk değerleri nedir?

‘‘6 + 3 > 7 dir.’’ (…..)

Cevabı Gör

1

‘‘En büyük iki negatif tam sayının toplamı -2 dir.’’ (…..)

Cevabı Gör

1

En büyük negatif tam sayı -1 dir. Sonraki ise -2 dir. Ancak, cümlede sayıların birbirinden farklı olduğu belirtilmemiş. Dolayısıyla ikisi de -1 seçilebilir. -1+(-1)=-2  doğru

‘‘Dünyada ilk kalorifer sistemi İshakpaşa Sarayı’nda kullanılmıştır.’’ (…..)

Cevabı Gör

1

‘‘10 ile 19 arasında 8 gerçek sayı vardır.’’ (…..)

Cevabı Gör

0

Tamsayı deseydi doğru olurdu. Gerçek sayı dedi için sonsuz sayı vardır. Mesela 10,2  10,25  10,25869 gibi örnek sayılar sonsuz defa yazılabilir ve bunlar 10 ile 19 arasındadır.

‘‘2 sayısı, 2x – 3 =1 denkleminin çözüm kümesinin bir elemanıdır.’’ (…..)

Cevabı Gör

1

2x=4, x=2  bulunur.

Alıştırma-3
Aşağıdaki önermelerden hangileri birbirine denktir?

p : ‘‘Mardin ili, Güney Doğu Anadolu Bölgesi’ndedir.’’
q : ’’32 –22  < (-2)2 dir.’’
r : ‘‘Negatif asal sayı yoktur.’’
\displaystyle s:''\frac{{{{{\left( {-2} \right)}}^{2}}\cdot {{{\left( {-1} \right)}}^{{101}}}}}{{{{{\left( {-3} \right)}}^{2}}+{{{\left( {-5} \right)}}^{2}}}}>0\text{ }d\imath r.''

Cevabı Gör

p  önermesi doğrudur. p≡ 1

q : ’’32 –22  < (-2)2 dir.’’  9-4<4    ,  9<8   yanlış.  q≡ 0

r  önermesi doğrudur. p≡ 1

s önermesini inceleyelim.

\displaystyle \frac{{{{{\left( {-2} \right)}}^{2}}\cdot {{{\left( {-1} \right)}}^{{101}}}}}{{{{{\left( {-3} \right)}}^{2}}+{{{\left( {-5} \right)}}^{2}}}}>0

\displaystyle \frac{{4\cdot \left( {-1} \right)}}{{9+25}}>0

\displaystyle \frac{{-4}}{{34}}>0

Yanlış. s≡ 0

O halde,  p ile r birbirlerine denk, q ile de s birbirine denktir. Şu şekilde gösterebiliriz.

p ≡ r    ve  q ≡ s   

Alıştırma-4
Önermelerin olumsuzlarını ifade ediniz.

p : ‘‘Fındık üretiminde Türkiye dünya birincisidir.”

Cevabı Gör

p’ : ‘‘Fındık üretiminde Türkiye dünya birinci değildir.”

q : ‘‘3x + 5 > -2 ifadesini sağlayan en küçük x tam sayı değeri -3 tür.’’

Cevabı Gör

q’ : ‘‘3x + 5 > -2 ifadesini sağlayan en küçük x tam sayı değeri -3 değildir.’’

\displaystyle r:\text{ '' }\frac{1}{2}+\frac{1}{4}:\frac{1}{2}=1\text{ dir}\text{.''}

Cevabı Gör

\displaystyle r':\text{ '' }\frac{1}{2}+\frac{1}{4}:\frac{1}{2}\ne 1\text{ dir}\text{.''}

Alıştırma-5
Doğruluk durumu sayısı

7 farklı önermenin birbirine göre kaç tane doğruluk durumu vardır?

Cevabı Gör

27=128 tane

Alıştırma-6
Doğruluk durumu sayısı

n + 2 tane farklı önermenin birbirine göre 64 farklı doğruluk durumu olduğuna göre n sayısını bulunuz.

Cevabı Gör

\displaystyle {{2}^{{n+2}}}=64

\displaystyle {{2}^{{n+2}}}={{2}^{6}}

\displaystyle n+2=6

\displaystyle n=4\text{ buluruz}\text{.}

2.sayfaya geçmek için tıklayınız.

Sayfalar: 1 2 3 4 5 6

“Mantık” üzerine 4 yorum

  4. Hocam merhabalar yeni başlamış bir öğretmen olarak bilgilerinizden faydalanırken her seferinde Allah razı olsun diyorum işimi çok kolaylaştırıyor Teşekkür ederim böyle net anlatım ve bilgiler için .

Yorum yapın