 İkinci Dereceden Bir Bilinmeyenli Denklemler
İkinci Dereceden Bir Bilinmeyenli Denklemler
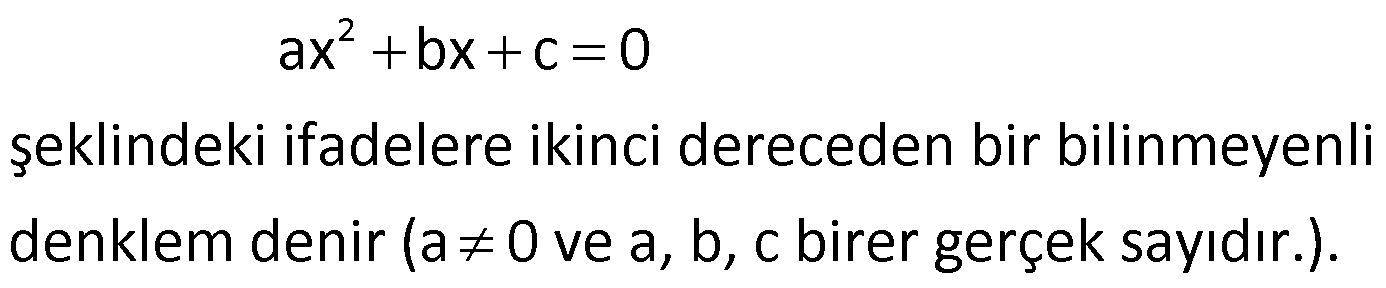
Örnek:

Çözüm:

Örnek:
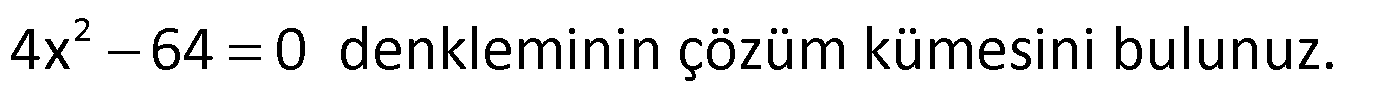
Çözüm:
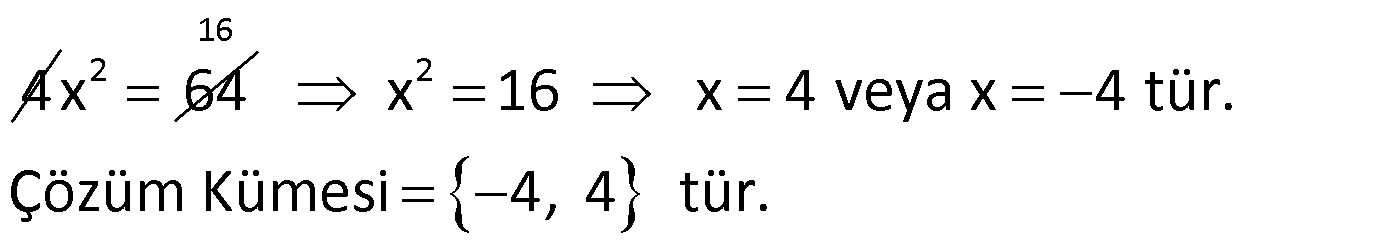
Örnek:
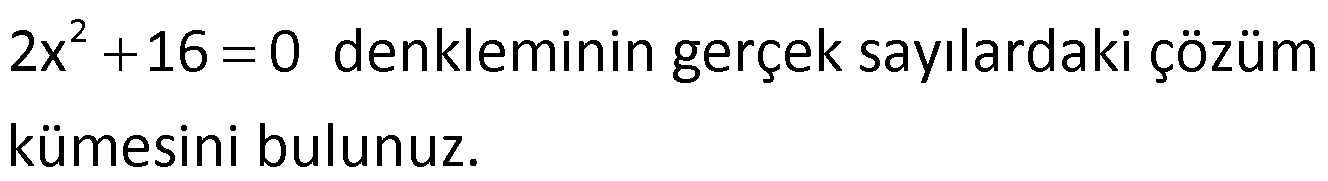
Çözüm:

Çarpanlara Ayırma Yöntemi ile Denklem Çözme
Verilen ifadeyi çarpanlara ayırdıktan sonra her bir çarpan 0’a eşitlenir.
Örnek:
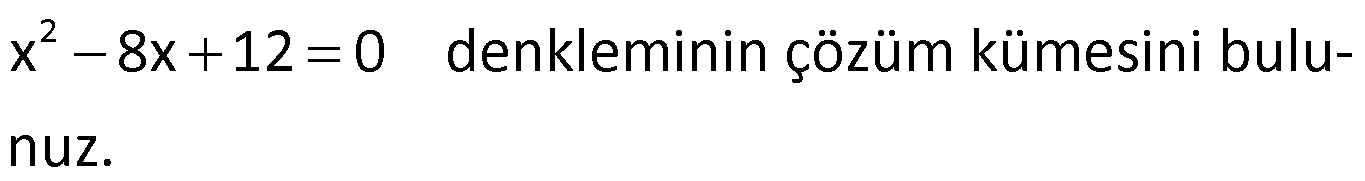
Çözüm:
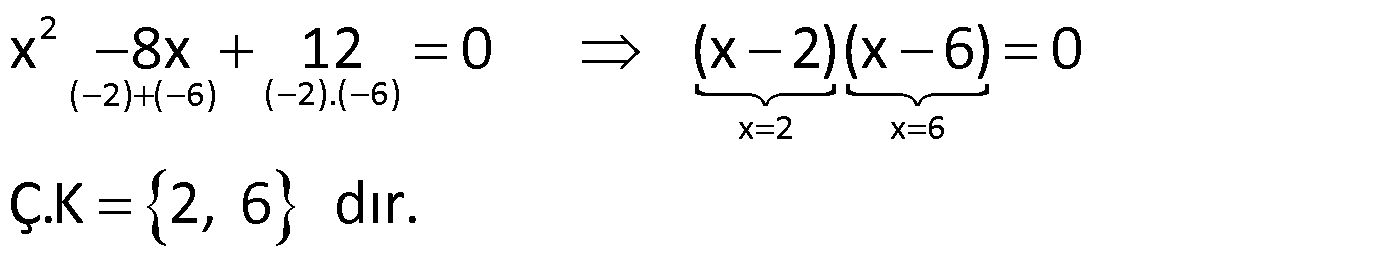
Örnek:
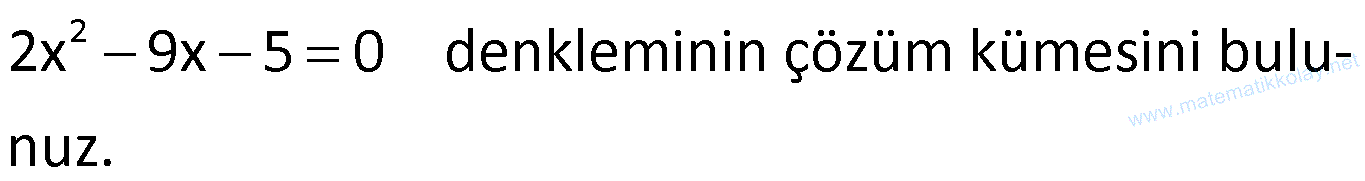
Çözüm:
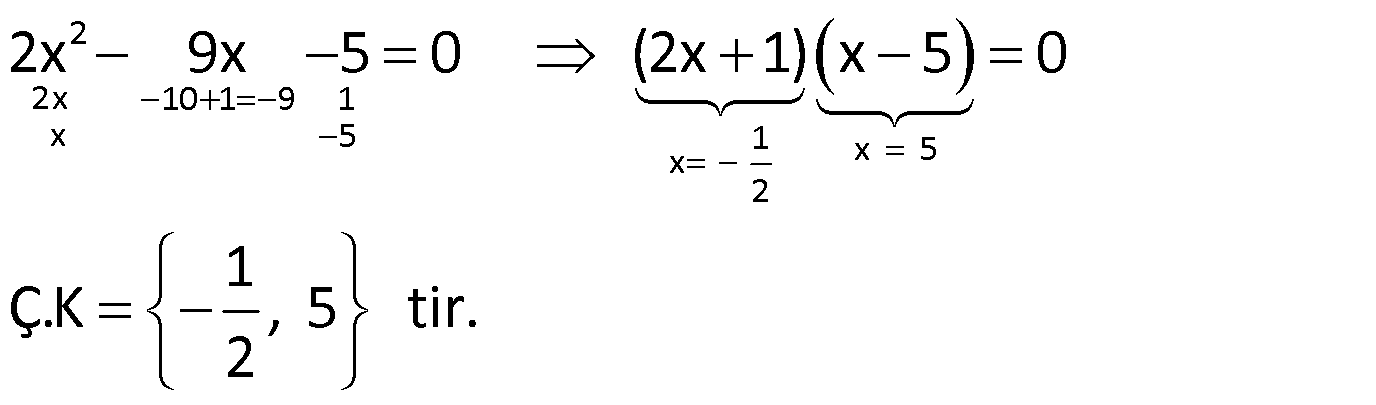
Örnek:
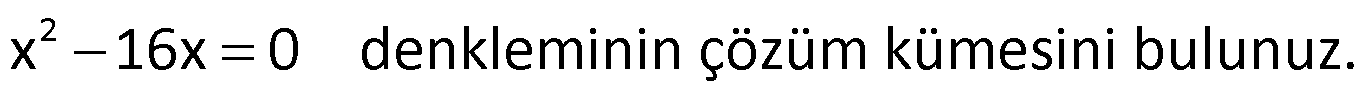
Çözüm:

Örnek:
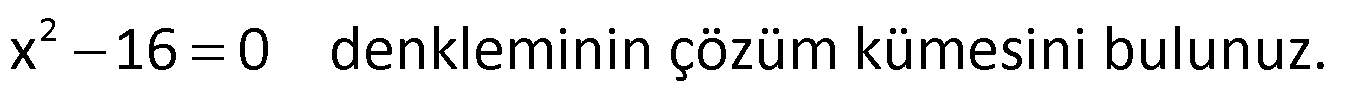
Çözüm:
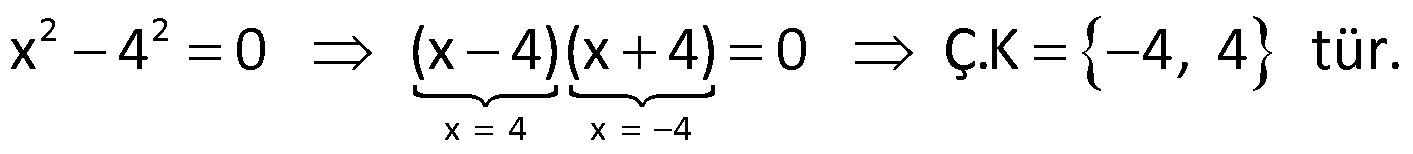
Örnek:
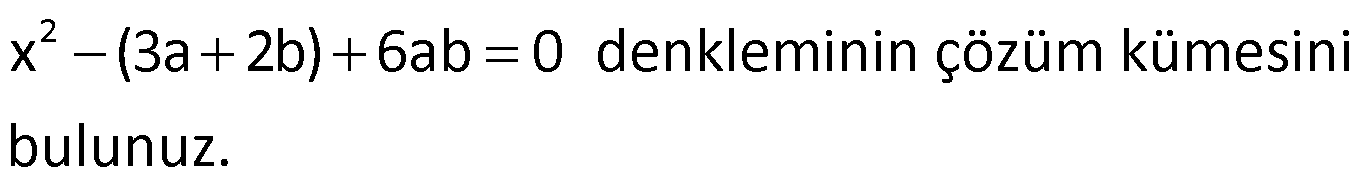
Çözüm:
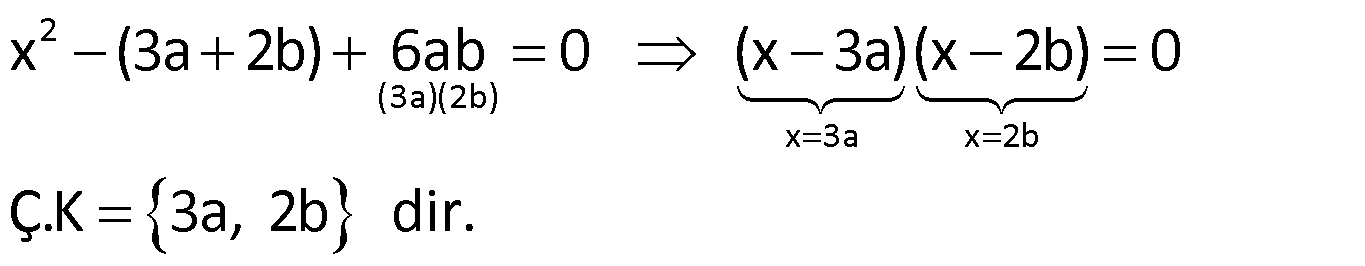
Örnek:

Çözüm:

Örnek:

Çözüm:

Örnek:
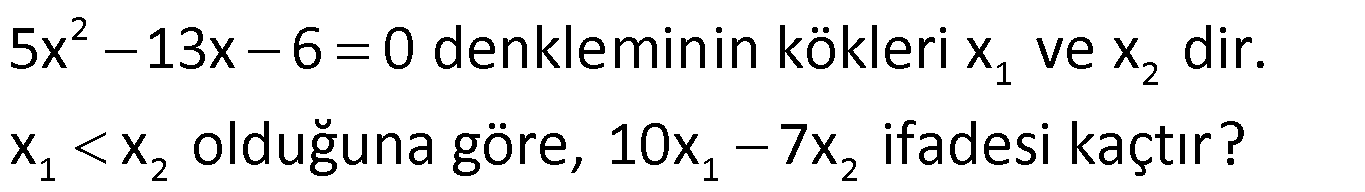
Çözüm:
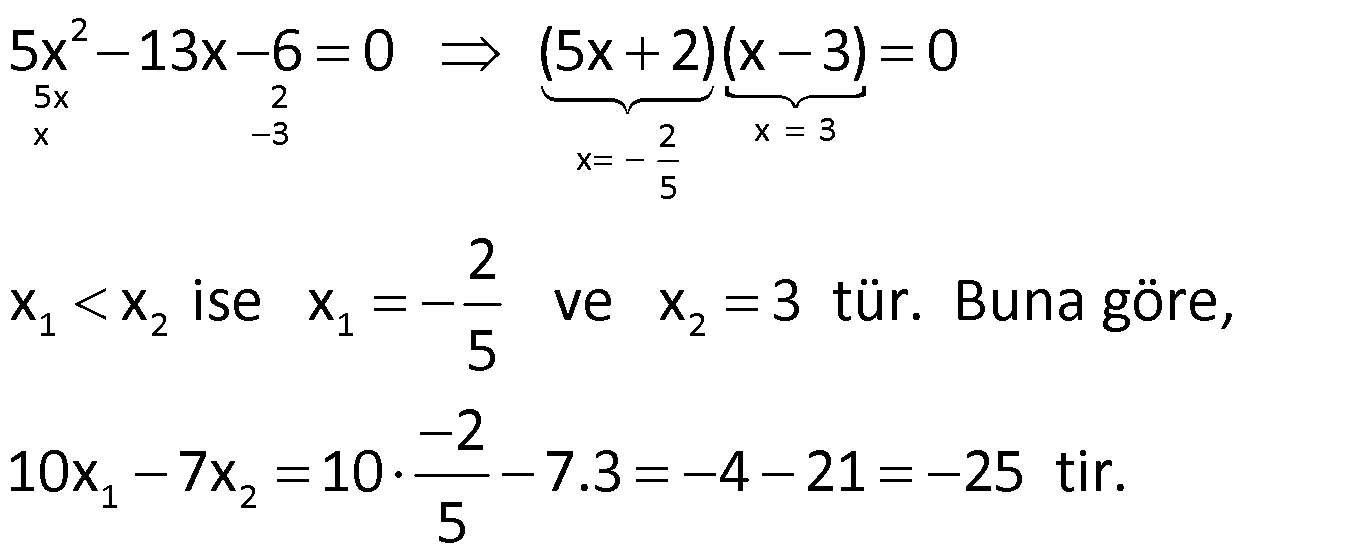
Örnek:
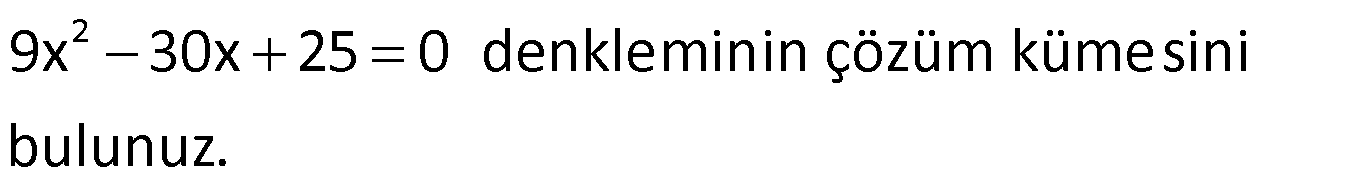
Çözüm:

Örnek:
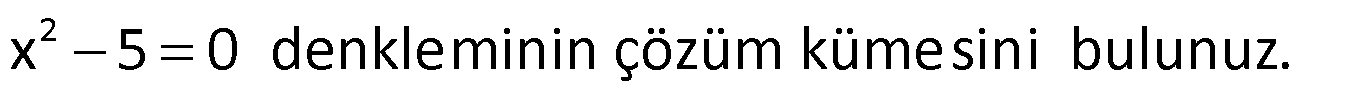
Çözüm:
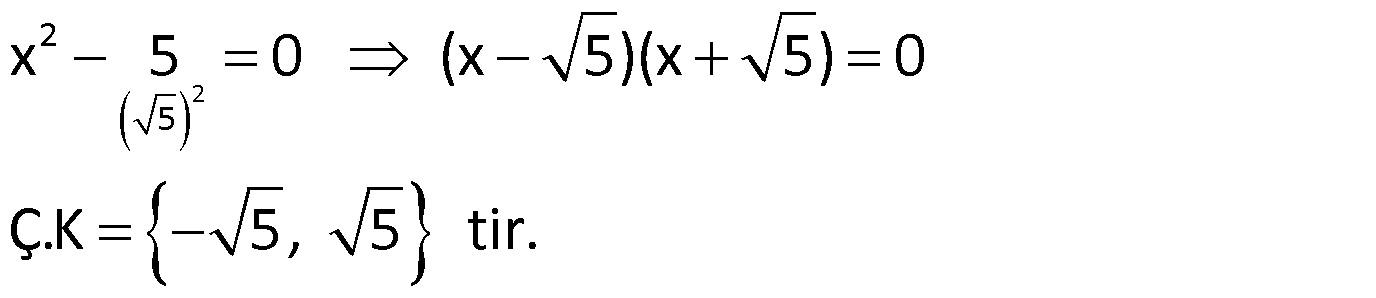
Örnek:
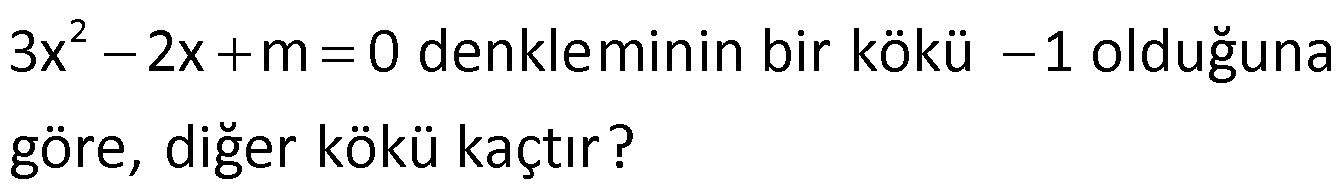
Çözüm:
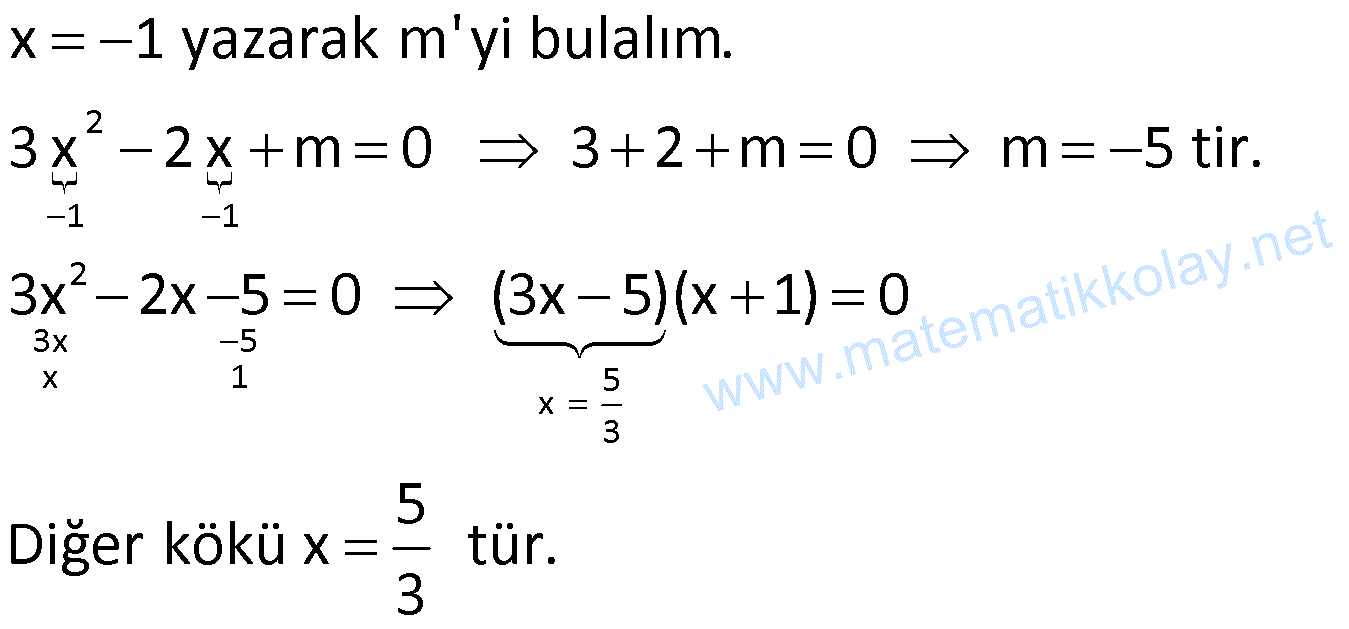
Değişken Değiştirme Yöntemi Kök Bulma
Bazen, ikinci dereceden olmayan ifadeleri değişken değiştirerek ikinci dereceden denklem haline getirebiliriz.
Örnek:
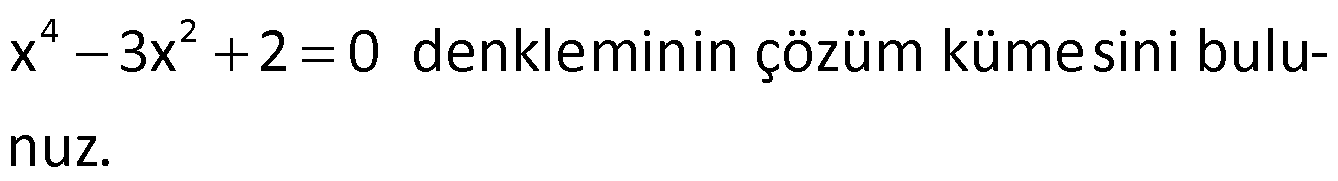
Çözüm:

Örnek:
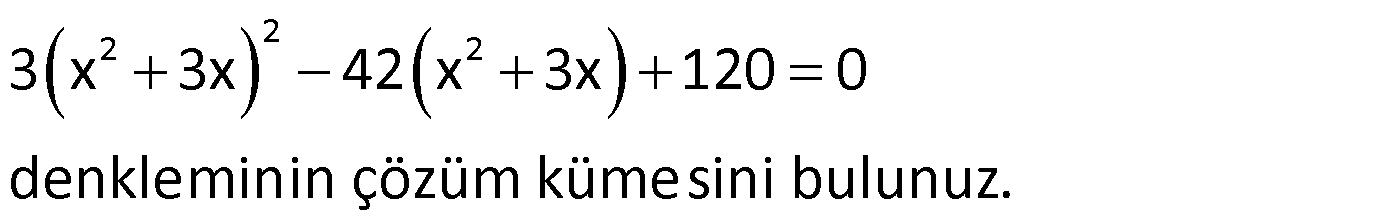
Çözüm:

Örnek:
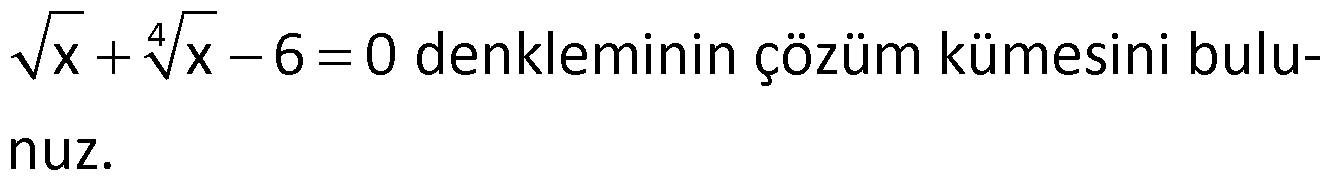
Çözüm:

Örnek:
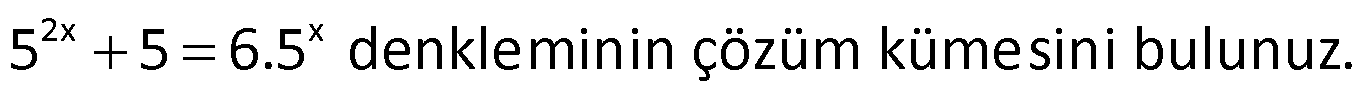
Çözüm:
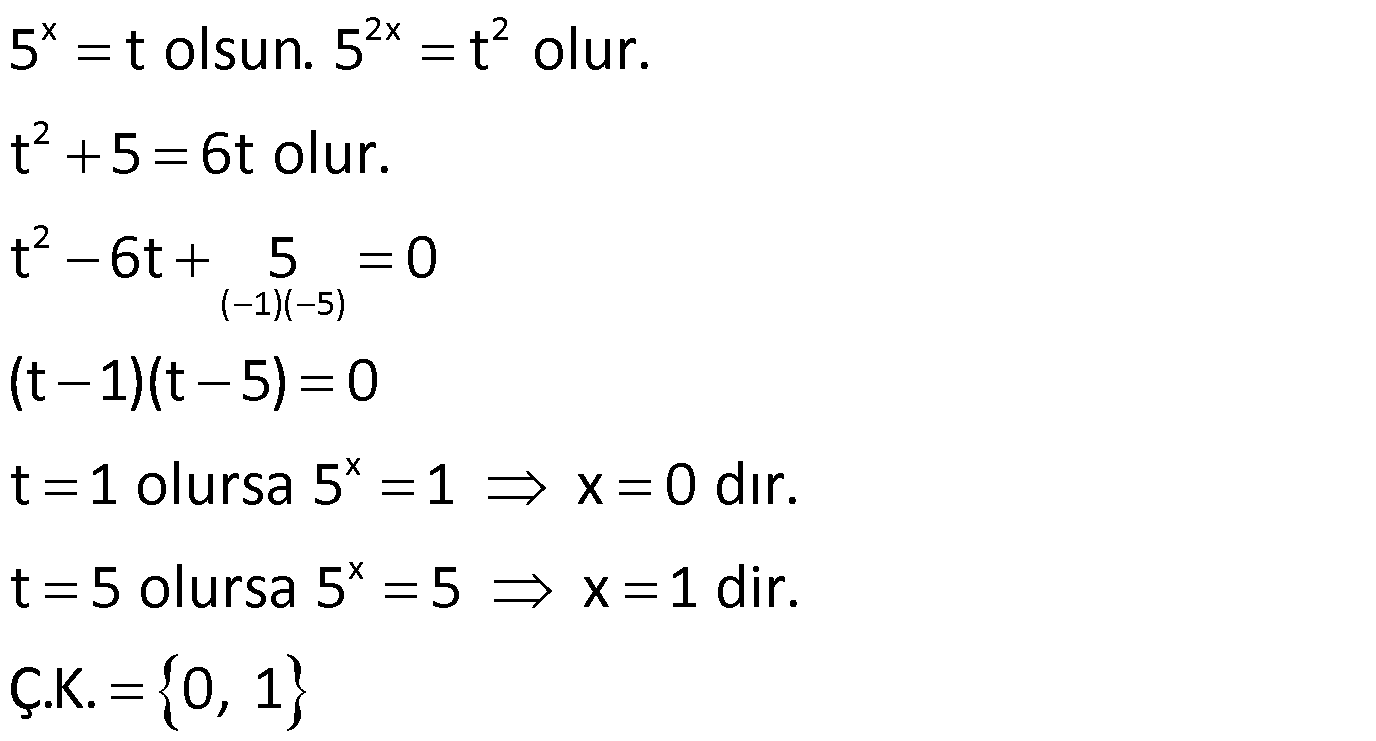
Tam Kareye Tamamlayarak Kök Bulma
Verilen ifadelerde terim ekleyip çıkararak tam kare ifadeler oluşturabiliriz. Sonra rahatlıkla çarpanlarına ayırarak çözüm kümesini bulabiliriz.
Örnek:

Çözüm:

Örnek:
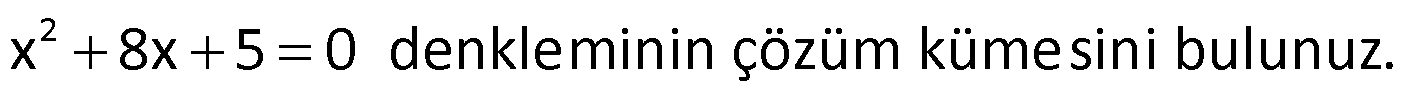
Çözüm:

Örnek:
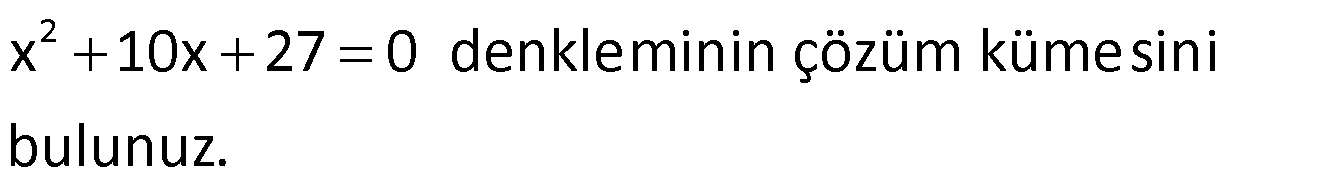
Çözüm:

Diskriminant ile Kök Bulma (Genel Çözüm)
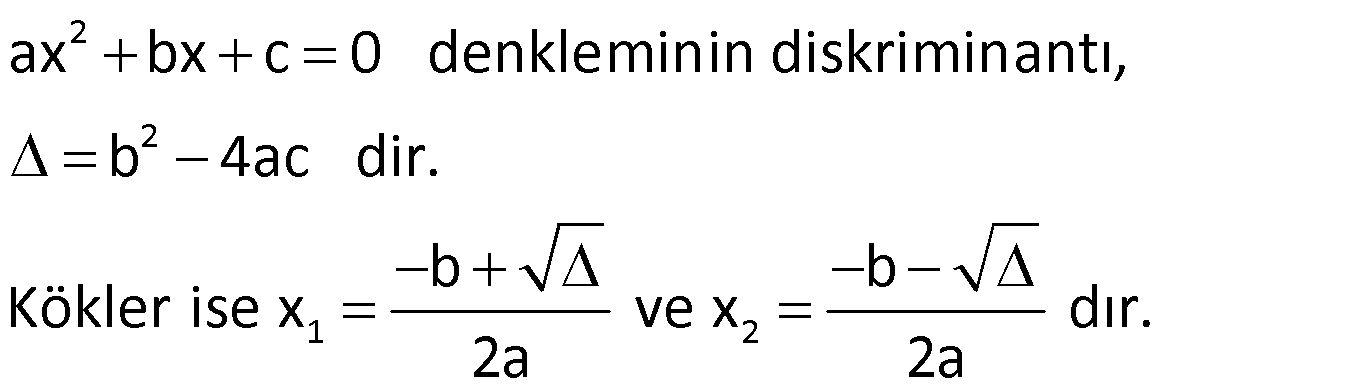
Not: Diskriminant formülü, lise matematiğindeki en önemli formüllerden biridir.
Örnek:
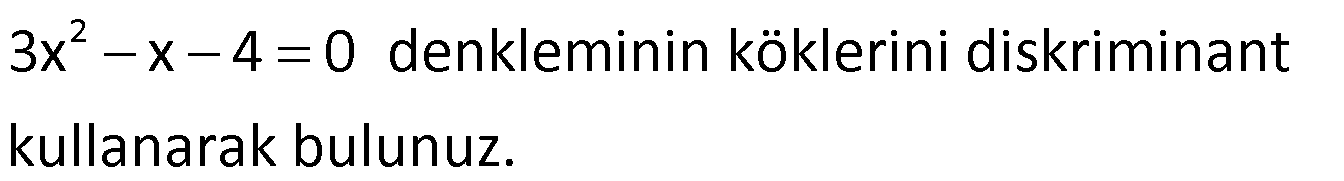
Çözüm:
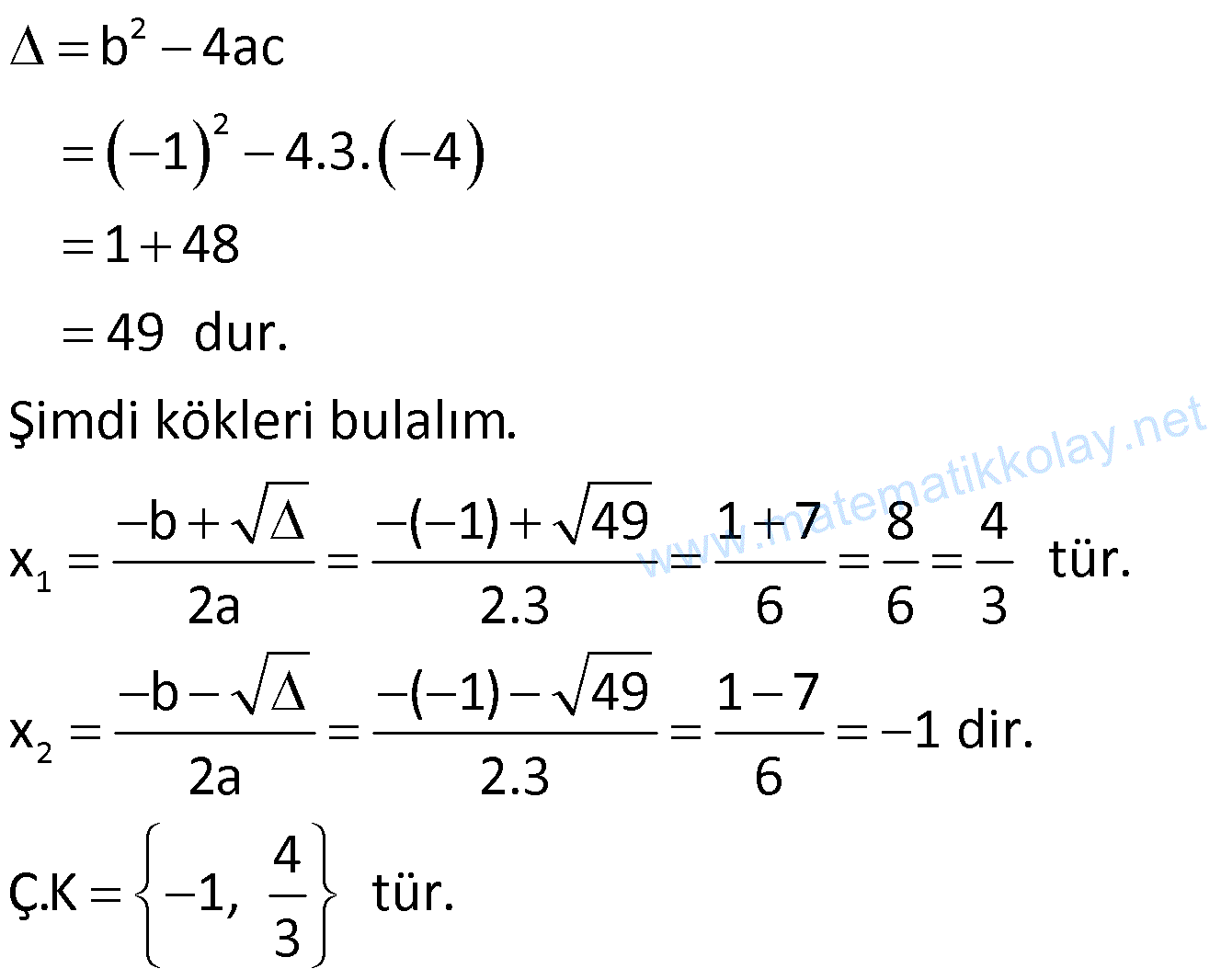
Örnek:

Çözüm:

Köklerin Varlığı
Denklemin diskriminantına göre, gerçek köklerin olup olmadığına karar verebiliriz.

Örnek:

Çözüm:

Örnek:
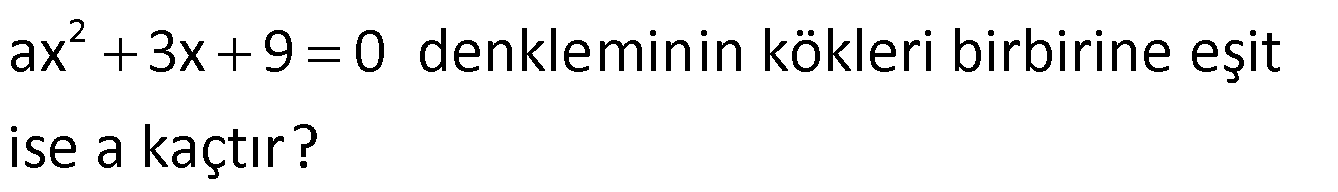
Çözüm:
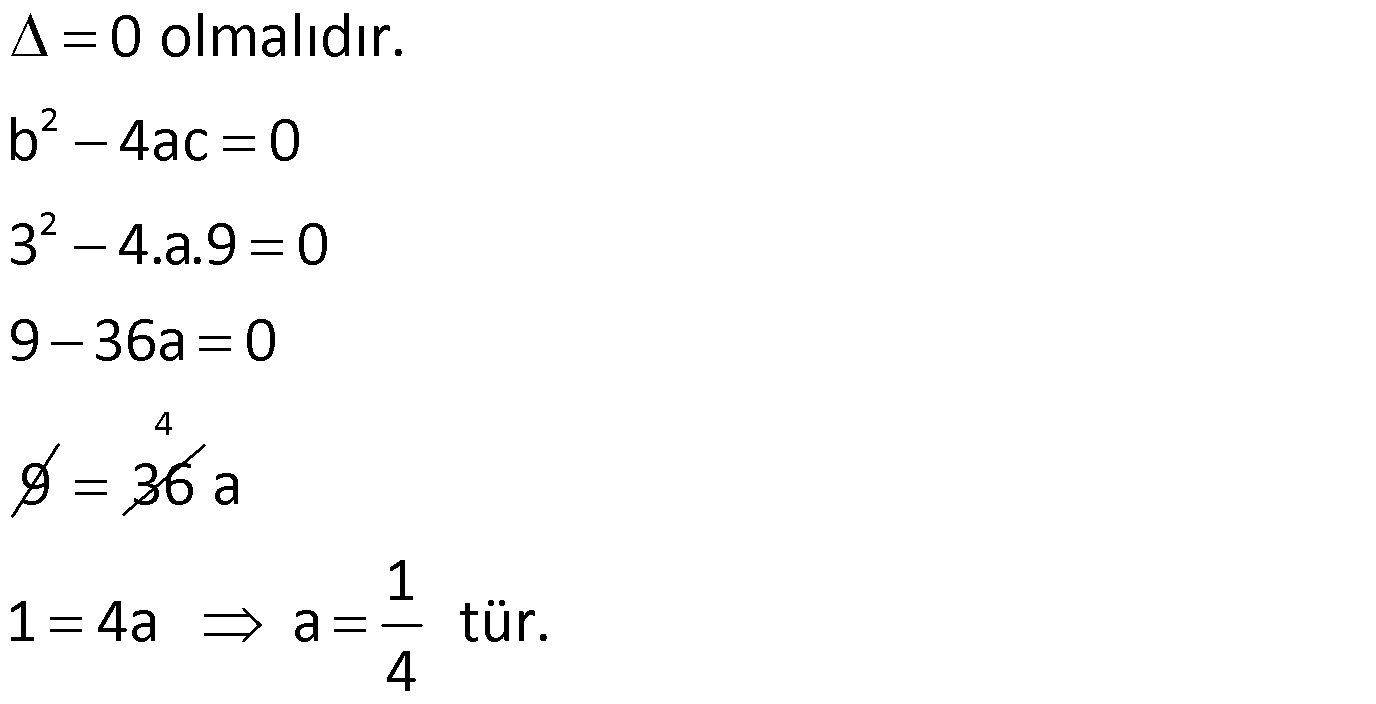
Örnek:
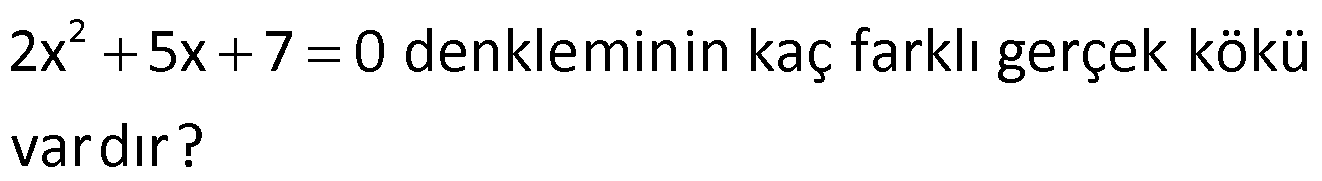
Çözüm:
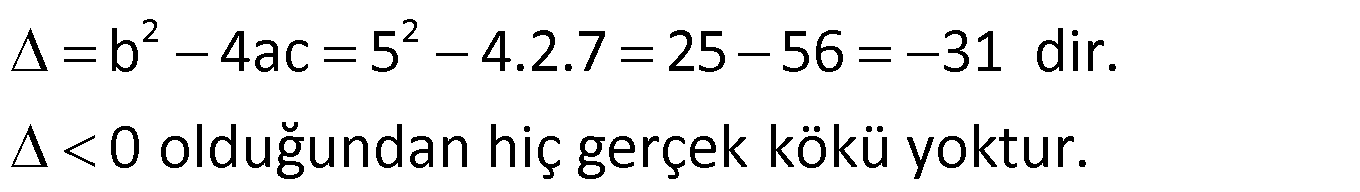
Not:

Örnek:

Çözüm:

Kökler ile Katsayılar Arasındaki İlişkiler

Örnek:
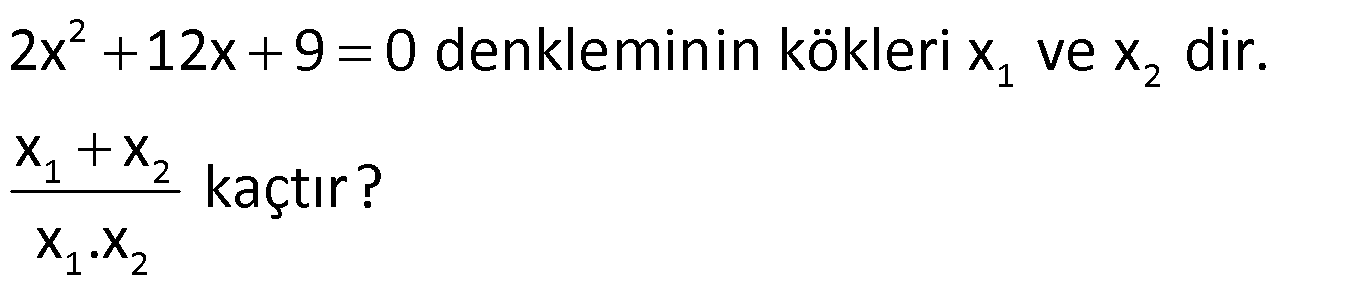
Çözüm:
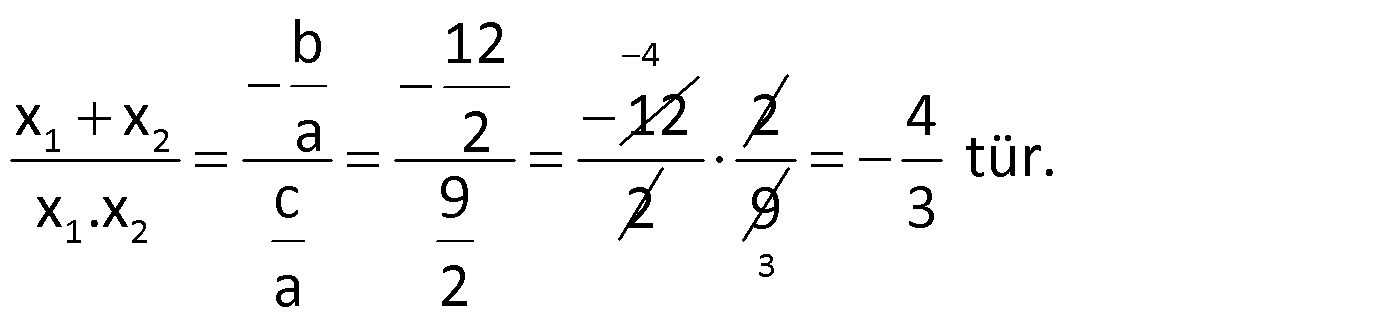
Örnek:
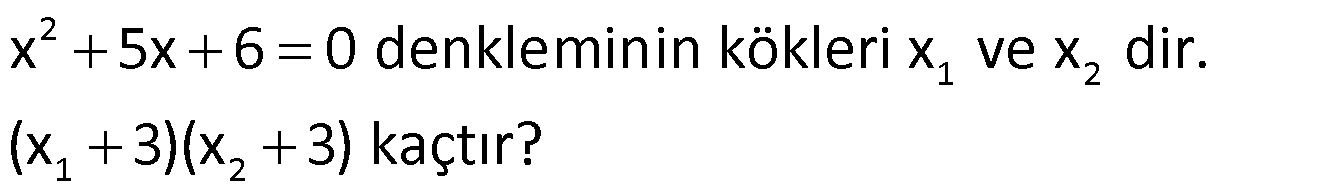
Çözüm:
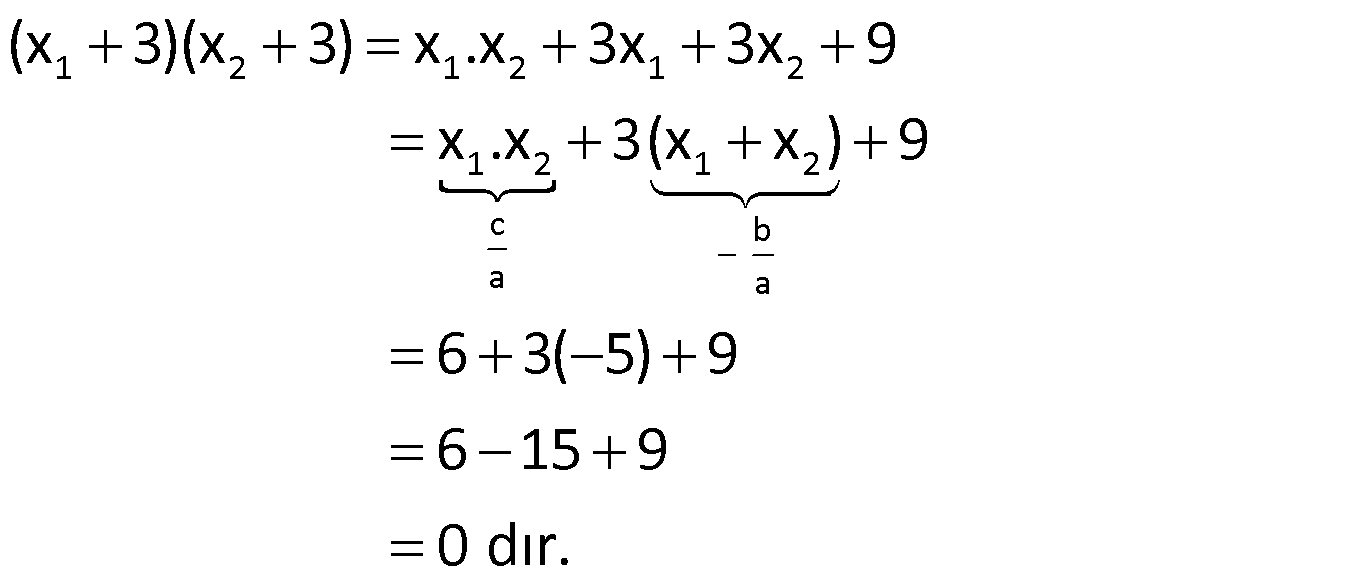
Örnek:

Çözüm:
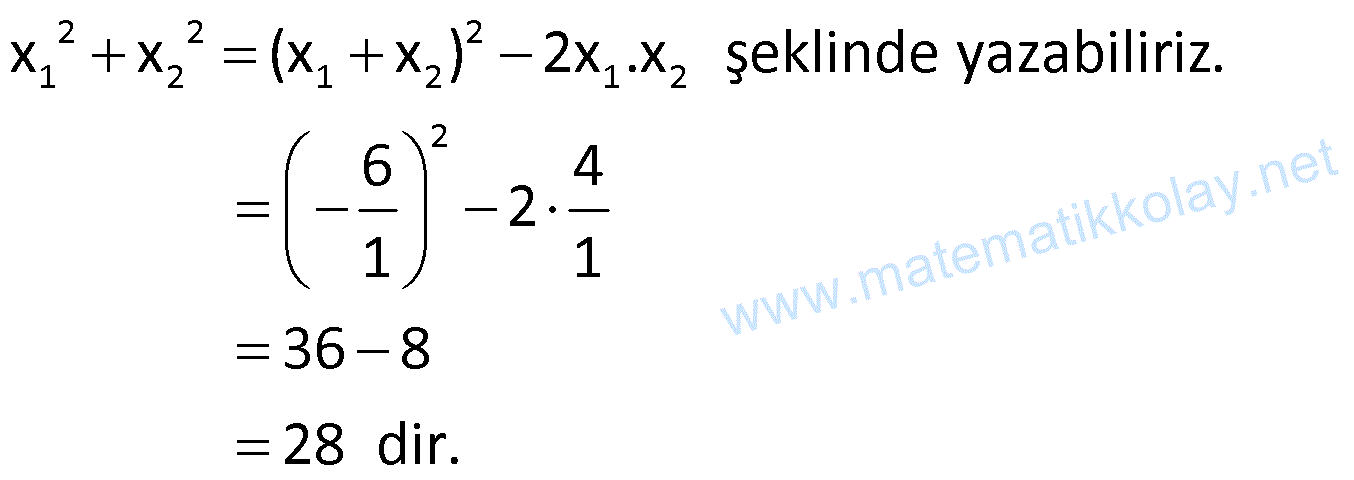
Örnek:

Çözüm:
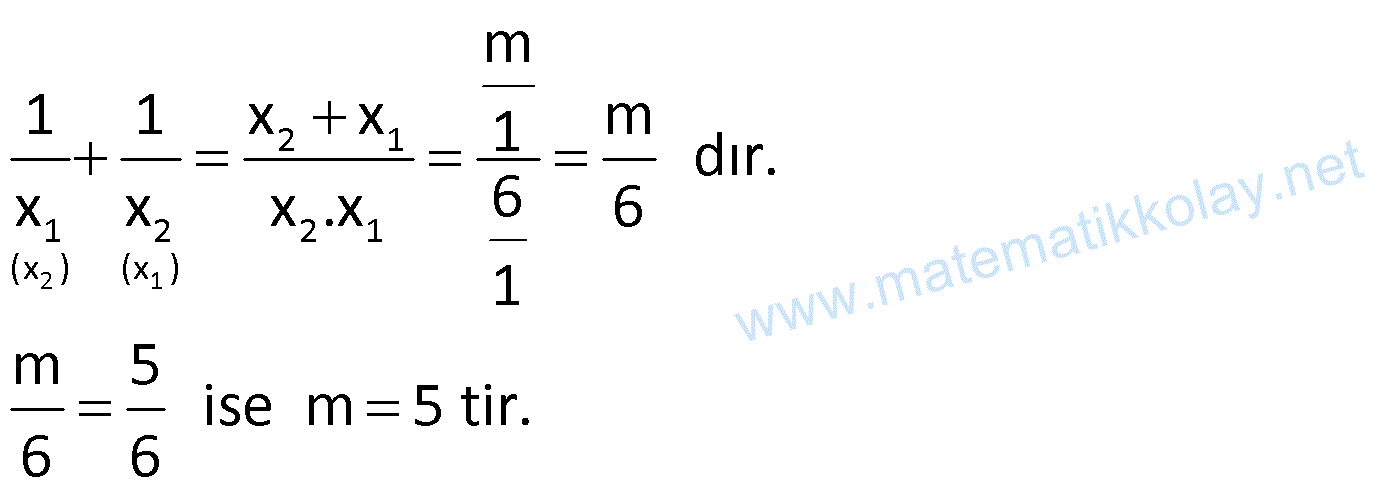
Örnek:
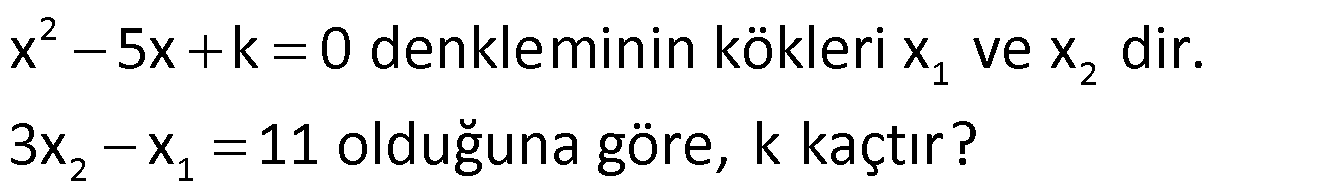
Çözüm:
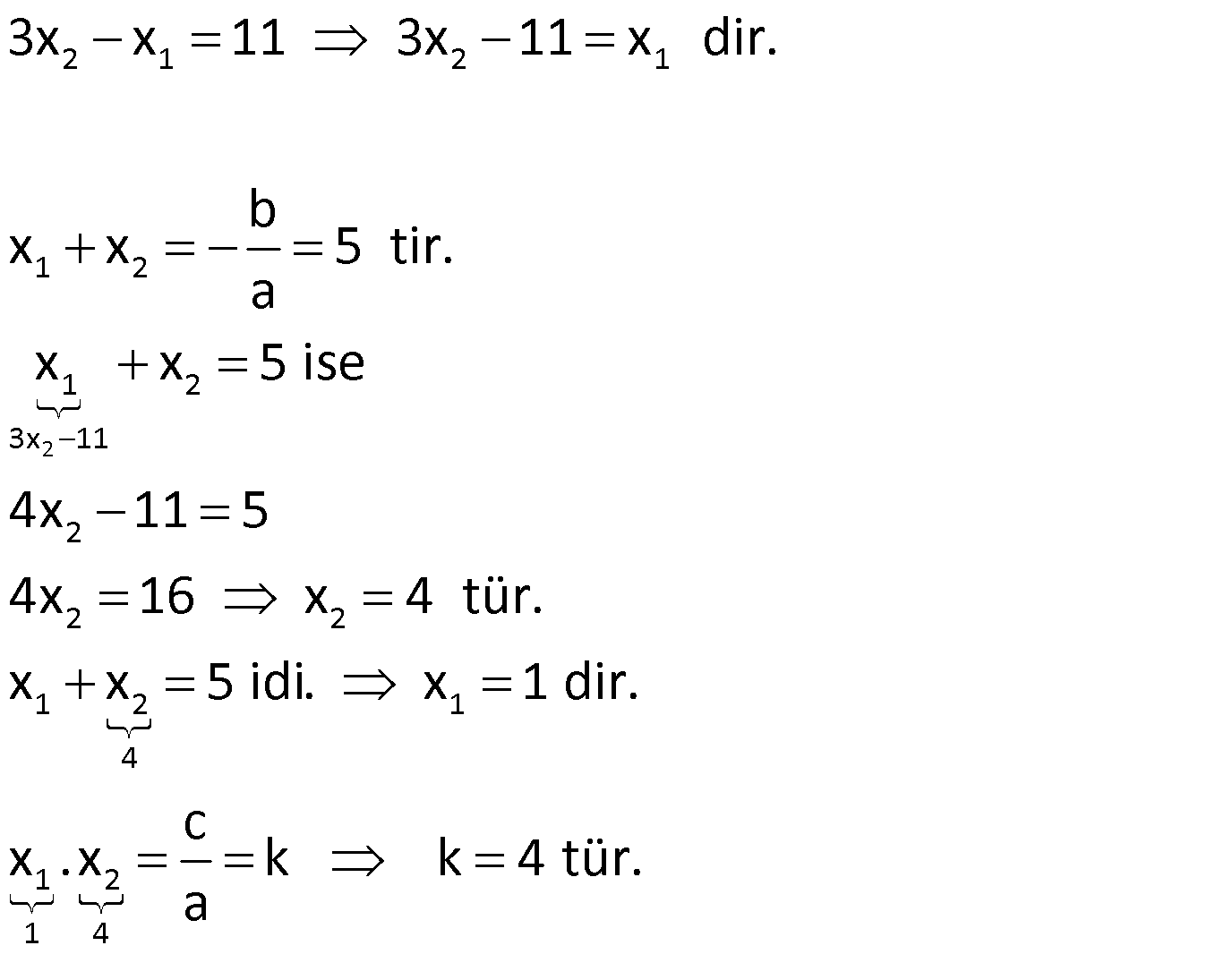
Örnek:
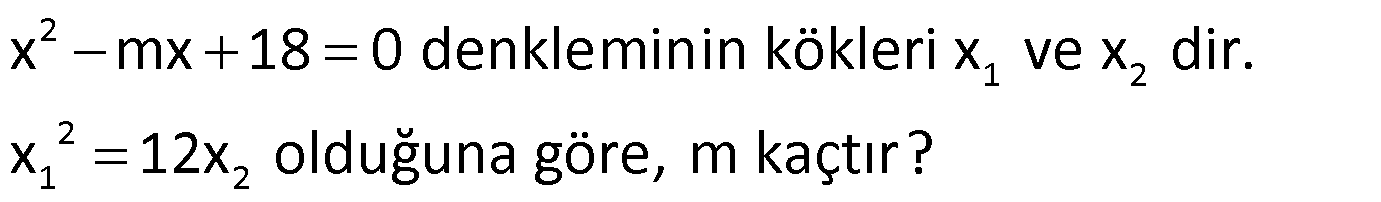
Çözüm:

Örnek:
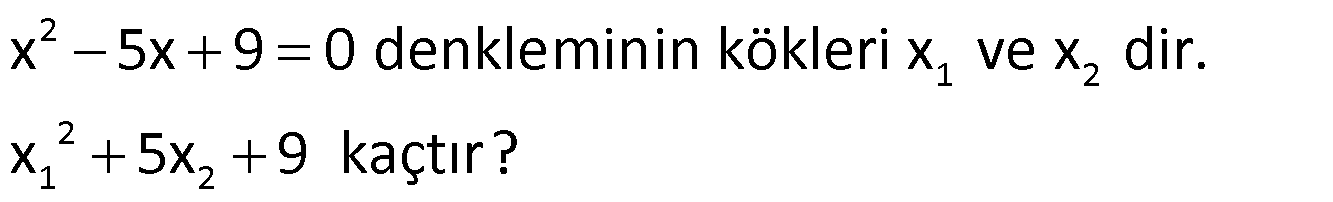
Çözüm:

Kökleri Verilen İkinci Dereceden Denklemi Elde Etme

Örnek:

Çözüm:

Örnek:
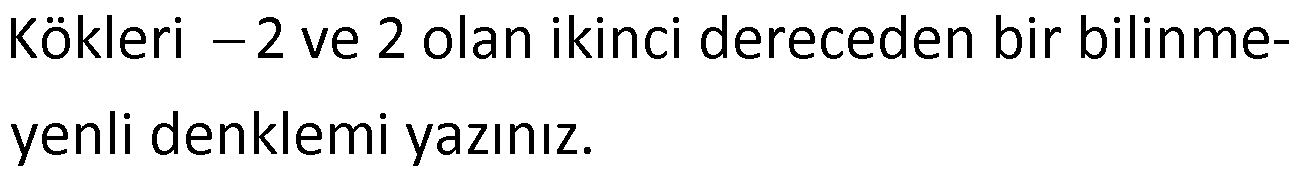
Çözüm:
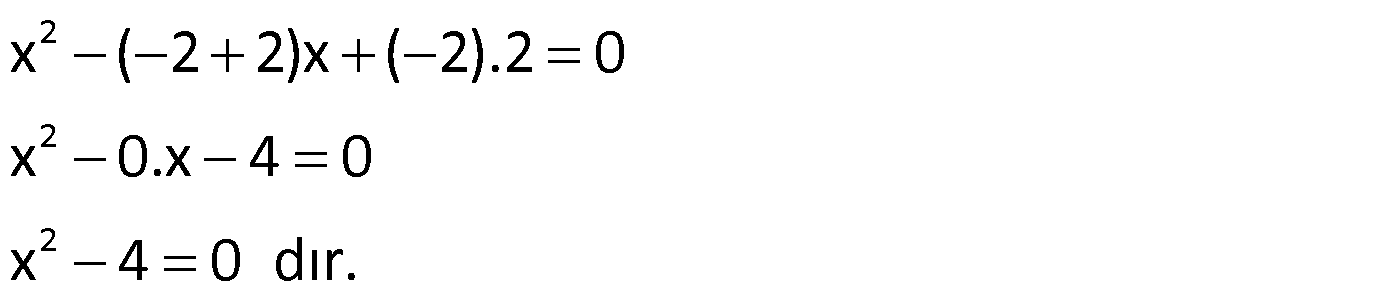
Örnek:
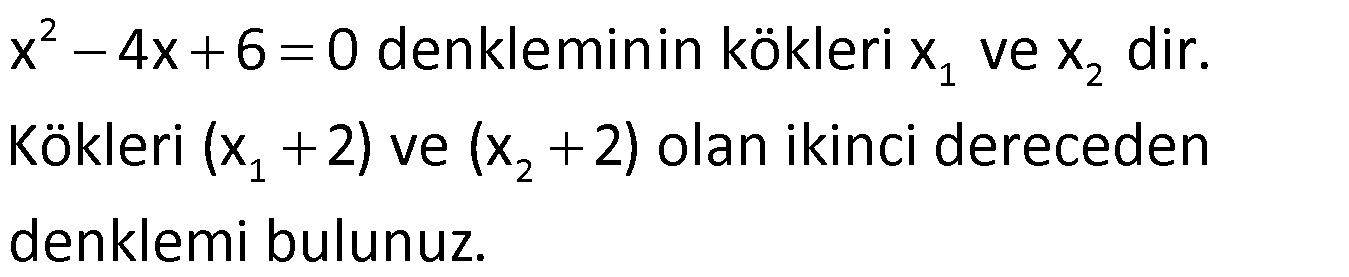
Çözüm:

Örnek:
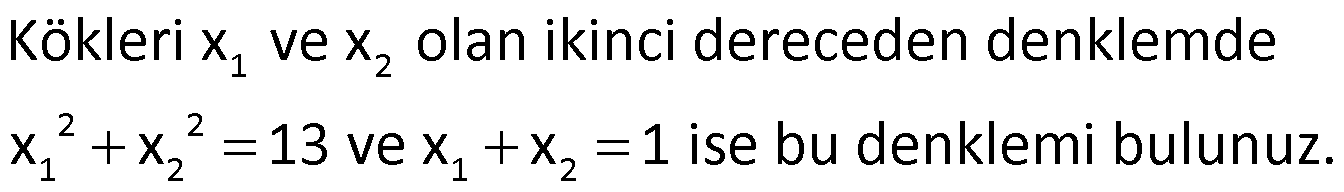
Çözüm:
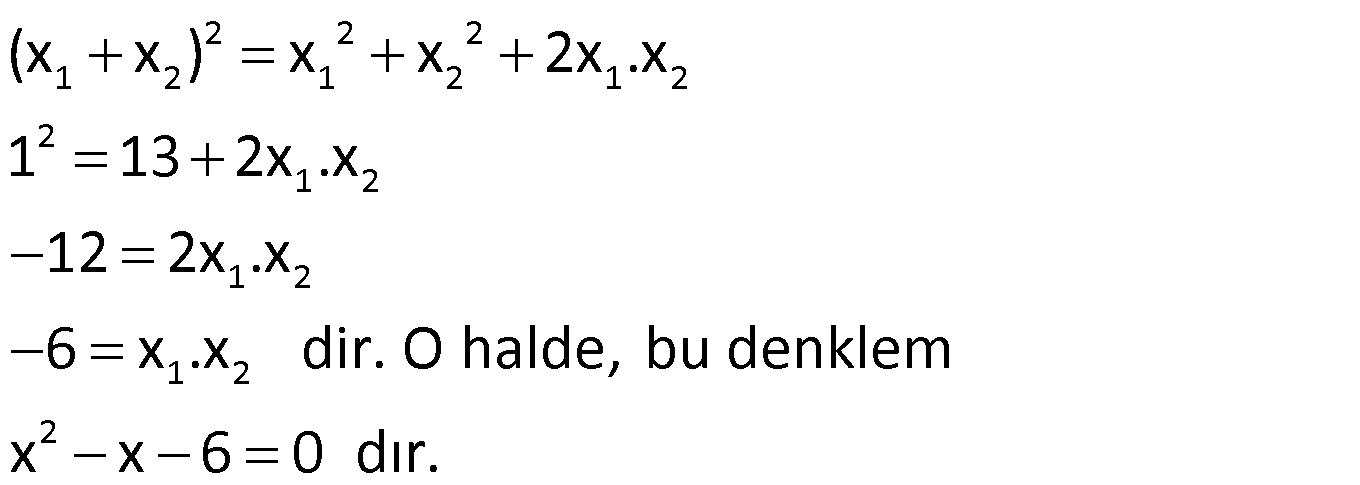
Not:
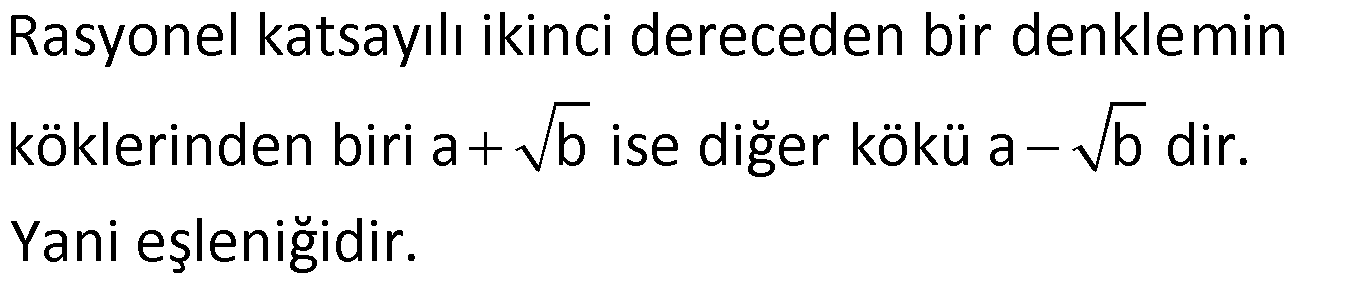
Örnek:

Çözüm:
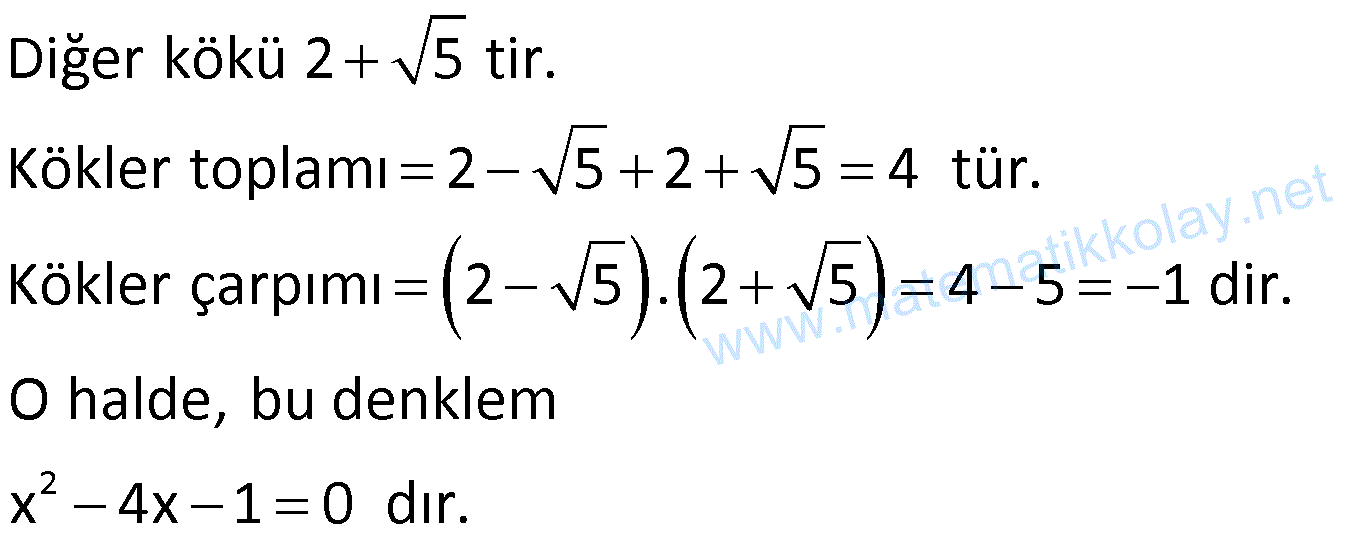
Not: (Kökler Karmaşık Sayı ise)

Örnek:

Çözüm:
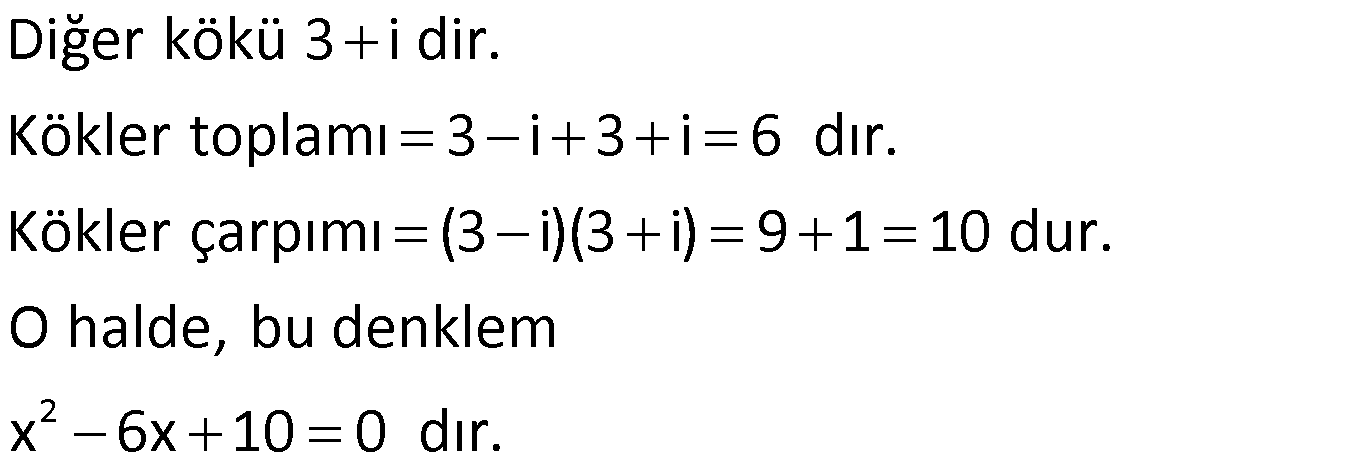
Not:

Örnek:

Çözüm:

Not: İki denklemin kökleri aynı ise katsayıları oranı eşittir.
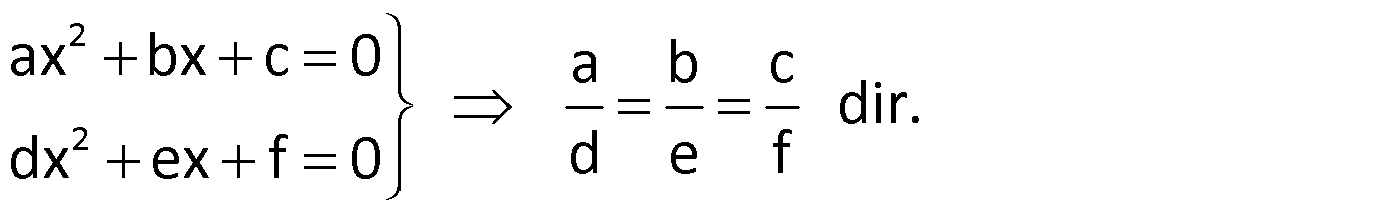
Örnek:

Çözüm:

Çözümlü Sorular veya Çıkmış Sorular için Tıkla
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
2.DERECEDEN DENKLEMLER KONU ANLATIMI www.matematikkolay.net İkinci Dereceden Bir Bilinmeyenli Denklemler 2 ax bx c 0 şeklindeki ifadelere ikinci dereceden bir bilinmeyenli denklem denir (a 0 ve a, b, c birer gerçek sayıdır.). Örnek: 3 2 (m 3)x 2x 5x n 0 denklemi ikinci dereceden bir bilinmeyenli denklem olup bir kökü 1 dir. Buna göre, m n kaçtır? Çözüm: 3 2 1 1 İkinci dereceden bir denklem olduğundan x lü terimin katsayısı 0 olmalıdır. m 3 0 m 3 tür. Denklemin bir kökü 1 ise, x yerine yazıp n’yi bulabiliriz. 2 x 5 x n 0 2 5 n 0 n 3 tür. m n 3 3 6 buluruz. Örnek: 2 4x 64 0 denkleminin çözüm kümesini bulunuz. Çözüm: 4 2 x 64 16 2 x 16 x 4 veya x 4 tür. Çözüm Kümesi 4, 4 tür. Örnek: 2 2x 16 0 denkleminin gerçek sayılardaki çözüm kümesini bulunuz. Çözüm: 2 2 2x 16 x 8 Hiç bir gerçek sayının karesi negatif olmadığı için Gerçek sayılardaki çözüm kümesi boş kümedir. Çarpanlara Ayırma Yöntemi ile Denklem Çözme Verilen ifadeyi çarpanlara ayırdıktan sonra her bir çarpan 0’a eşitlenir. Örnek: 2 x 8x 12 0 denkleminin çözüm kümesini bulunuz. Çözüm: 2 ( 2) ( 6) ( 2).( 6) x 2 x 6 x 8x 12 0 (x 2)(x 6) 0 Ç.K 2, 6 dır. Örnek: 2 2x 9x 5 0 denkleminin çözüm kümesini bulunuz. Çözüm: 2 2x 10 1 9 1 x 5 1 x 5 x 2 2x 9x 5 0 (2x 1) x 5 0 1 Ç.K , 5 tir. 2 Örnek: 2 x 16x 0 denkleminin çözüm kümesini bulunuz. Çözüm: x 0 x 16 2 2 x (x 16) 0 Ç.K 0, 16 dır. Lütfen aşağıdaki hatayı yapmayınız. x 16x 0 x Uyarı : x 16 x x 16 dır. Böyle yaparsak, x 0 kökünü kaçırmış oluruz. Örnek: 2 x 16 0 denkleminin çözüm kümesini bulunuz. Çözüm: 2 2 x 4 x 4 x 4 0 (x 4)(x 4) 0 Ç.K 4, 4 tür. Örnek: 2 x (3a 2b) 6ab 0 denkleminin çözüm kümesini bulunuz. www.matematikkolay.net Çözüm: 2 (3a)(2b) x 3a x 2b x (3a 2b) 6ab 0 (x 3a)(x 2b) 0 Ç.K 3a, 2b dir. Örnek: 2 Dikdörtgen şeklindeki bir bahçenin kısa kenarı (x 2) metre, uzun kenarı ise (2x+3) metredir. Bu bahçenin alanı 22 m olduğuna göre, x kaçtır? Çözüm: 2 2 x 4 2x 7 x 4 7 x 2 (x 2)(2x 3) 22 denklemi tahmin edilerek de çözülebilir ama biz burada 2.derece denklem çözerek yapacağız. İlk önce ifadeyi genişletelim. 2x 3x 4x 6 22 2x x 28 0 (x 4)(2x 7) 0 7 x yi alamayız çünkü uzunluklar pozitif olmalı. 2 x 4 tür. Örnek: 2 Bir hareketlinin zamana göre yüksekliği metre cinsinden f(t) t 12t 16 fonksiyonu ile ifade ediliyor. O halde bu hareketli kaçıncı saniyelerde yerden 48 metre yukarıdadır? Çözüm: 2 2 t 8 t 4 t 8 t 4 t 12t 16 48 denkleminin çözümü soruluyor. t 12t 32 0 ( t 8)(t 4) 0 4. ve 8. saniyelerde yerden 48 metre yukarıdadır. Örnek: 2 1 2 1 2 1 2 5x 13x 6 0 denkleminin kökleri x ve x dir. x x olduğuna göre, 10x 7x ifadesi kaçtır? Çözüm: 2 5x 2 x 3 2 x 3 x 5 1 2 1 2 1 2 5x 13x 6 0 (5x 2)(x 3) 0 2 x x ise x ve x 3 tür. Buna göre, 5 2 10x 7x 10 7.3 4 21 25 tir. 5 Örnek: 2 9x 30x 25 0 denkleminin çözüm kümesini bulunuz. Çözüm: 2 2 2 2 (3x) 2.3x.5 5 1 2 5 9x 30x 25 0 (3x 5) 0 x tür. 3 x x dir. Eşit iki kökü vardır. 5 Çözüm kümesi bir elemanlıdır. Ç.K= 3 Örnek: 2 x 5 0 denkleminin çözüm kümesini bulunuz. Çözüm: 2 2 5 x 5 0 (x 5)(x 5) 0 Ç.K 5, 5 tir. Örnek: 2 3x 2x m 0 denkleminin bir kökü 1 olduğuna göre, diğer kökü kaçtır? Çözüm: 2 1 1 2 3x 5 x 1 5 x 3 x 1 yazarak m’ yi bulalım. 3 x 2 x m 0 3 2 m 0 m 5 tir. 3x 2x 5 0 (3x 5)(x 1) 0 5 Diğer kökü x tür. 3 Değişken Değiştirme Yöntemi Kök Bulma Bazen, ikinci dereceden olmayan ifadeleri değişken değiştirerek ikinci dereceden denklem haline getirebiliriz. www.matematikkolay.net Örnek: 4 2 x 3x 2 0 denkleminin çözüm kümesini bulunuz. Çözüm: 2 2 2 ( 1)( 2) a 1 a 2 2 x a dersek, a 3a 2 0 şeklinde ikinci dereceden bir denklem elde ederiz. a 3a 2 0 (a 1)(a 2) 0 a 1 olduğunda x 1 demektir. x 1 ya da x 1 olur. a 2 oldu 2 ğunda x 2 demektir. x 2 ya da x 2 olur. Ç.K 2, 1,1, 2 dir. Örnek: 2 2 2 3 x 3x 42 x 3x 120 0 denkleminin çözümkümesini bulunuz. Çözüm: 2 2 3a 30 a 4 a 10 a 4 2 2 ( 2)(5) x 2 x 5 2 2 ( 1)(4) x 1 x 4 x 3x a dersek, 3a 42a 120 0 olur. 3a 30 a 4 0 a 10 olursa x 3x 10 x 3x 10 0 (x 2)(x 5) 0 a 4 olursa x 3x 4 x 3x 4 0 (x 1)(x 4) 0 Ç. K 5, 4, 1, 2 dir. Örnek: 4 x x 6 0 denkleminin çözüm kümesini bulunuz. Çözüm: 4 2 2 (3).( 2) 4 4 4 x t olsun. x t olur. t t 6 0 (t 3)(t 2) 0 t 3 olursa x 3 olmalı ama çift dereceli bir köklü ifade negatif olamaz. Burada kök yoktur. t 2 olursa x 2 olur. x 2 16 dır. Ç.K. 16 Örnek: 2x x 5 56.5 denkleminin çözüm kümesini bulunuz. Çözüm: x 2x 2 2 2 ( 1)( 5) x x 5 t olsun. 5 t olur. t 5 6t olur. t 6t 5 0 (t 1)(t 5) 0 t 1 olursa 5 1 x 0 dır. t 5 olursa 5 5 x 1 dir. Ç.K. 0, 1 Tam Kareye Tamamlayarak Kök Bulma Verilen ifadelerde terim ekleyip çıkararak tam kare ifadeler oluşturabiliriz. Sonra rahatlıkla çarpanlarına ayırarak çözüm kümesini bulabiliriz. Örnek: 2 x 6x 8 0 denkleminin çözüm kümesini tam kareye tamamlayarak bulunuz. Çözüm: 2 2 2 (x 3) 2 İfadeye 1 ekleyip çıkaralım. x 6x 8 1 1 0 x 6x 9 1 0 olur. (x 3) 1 0 Şimdi iki kare farkından, (x 3 1)(x 3 1) 0 şeklinde yazabiliriz. (x 2)(x 4) 0 Ç.K 4, 2 dir. Örnek: www.matematikkolay.net 2 x 8x 5 0 denkleminin çözüm kümesini bulunuz. Çözüm: 2 2 2 2 1 2 x 8x ifadesinin yanında 16 olursa tam kare olur. O halde, x 8x 5 ifadesine 11 ekleyip çıkaralım. x 8x 16 11 0 olur. (x 4) 11 0 (x 4 11)(x 4 11) 0 x 4 11 , x 4 11 dir. Ç.K 4 11, 4 11 Örnek: 2 x 10x 27 0 denkleminin çözüm kümesini bulunuz. Çözüm: 2 2 2 2 2 x 10x ifadesinin yanında 25 olursa tam kare olur. O halde, x 10x 27 ifadesini x 10x 25 2 0 olarak yazalım. (x 5) 2 0 (x 5) 2 olur. Tam kare ifadeler negatif olamaz. Bu sebeple, Ç.K dir. Diskriminant ile Kök Bulma (Genel Çözüm) 2 2 1 2 ax bx c 0 denkleminin diskriminantı, b 4ac dir. b b Kökler ise x ve x dır. 2a 2a Not: Diskriminant formülü, lise matematiğindeki en önemli formüllerden biridir. Örnek: 2 3x x 4 0 denkleminin köklerini diskriminant kullanarak bulunuz. Çözüm: 2 2 1 2 b 4ac 1 4.3. 4 1 48 49 dur. Şimdi kökleri bulalım. b ( 1) 49 1 7 8 4 x tür. 2a 2.3 6 6 3 b ( 1) 49 1 7 x 1 dir. 2a 2.3 6 4 Ç.K 1, tür. 3 Örnek: 2 x 6x 4 0 denkleminin köklerini bulunuz. Çözüm: 2 2 1 2 b 4ac 6 4.1. 4 36 16 52 dir. Şimdi kökleri bulalım. b 6 52 6 2 13 x 3 13 tür. 2a 2 2 b 6 52 6 2 13 x 3 13 tür. 2a 2 2 Ç.K 3 13, 3 13 tür. Köklerin Varlığı Denklemin diskriminantına göre, gerçek köklerin olup olmadığına karar verebiliriz. 0 ise farklı iki gerçek kökü var dır. 0 ise eşit iki gerçek kökü var dır. (Çakışık kökler, çift katlı kökler de denilir.) Kısaca, bu ifade tam karedir. 0 ise gerçek kök yoktur. Örnek: 2 5x 2x m 2 0 denkleminin iki farklı gerçek kökü olduğuna göre, m’nin en küçük tam sayı değeri kaçtır? Çözüm: www.matematikkolay.net 2 2 0 olmalıdır. b 4ac 0 ( 2) 4.5.( m 2) 0 4 20( m 2) 0 4 20m 40 0 20m 36 0 20m 36 m’nin en küçük tam sayı değeri 2 dir. Örnek: 2 ax 3x 9 0 denkleminin kökleri birbirine eşit ise a kaçtır? Çözüm: 2 2 0 olmalıdır. b 4ac 0 3 4.a.9 0 9 36a 0 9 36 4 a 1 1 4a a tür. 4 Örnek: 2 2x 5x 7 0 denkleminin kaç farklı gerçek kökü vardır? Çözüm: 2 2 b 4ac 5 4.2.7 25 56 31 dir. 0 olduğundan hiç gerçek kökü yoktur. Not: İkinci dereceden bir denklemin her zaman iki kökü vardır. Sadece gerçek sayılardan oluşan kökleri farklılık gösterebilir. 0 ise iki kökü vardır. ikisi de gerçektir. 0 ise iki kökü vardır. ikisi de gerçek ve birbirine eşittir. 0 ise iki kökü vardır. ikisi de sanaldır. Sanal kökler sonradan işlenecektir. Örnek: 2 (m 2)x 6x 3 0 denkleminin iki gerçek kökü olduğuna göre, m’nin alabileceği en büyük tam sayı değeri kaçtır? Çözüm: 2 2 iki gerçek kök demediği için 0 olmalıdır. b 4ac 0 6 4.(m 2).3 0 36 12.(m 2) 0 36 Farklı 3 12.(m 2) 3 m 2 5 m m en fazla 5 olabilir. Kökler ile Katsayılar Arasındaki İlişkiler 2 ax bx c 0 denkleminde b Kökler toplamı a c Kökler çarpımı dır. a Örnek: 2 1 2 1 2 1 2 2x 12x 9 0 denkleminin kökleri x ve x dir. x x kaçtır? x .x Çözüm: 1 2 1 2 b 12 x x a 2 12 x .x c 9 a 2 4 2 2 9 3 4 tür. 3 Örnek: 2 1 2 1 2 x 5x 6 0 denkleminin kökleri x ve x dir. (x 3)(x 3) kaçtır? Çözüm: www.matematikkolay.net 1 2 1 2 1 2 1 2 1 2 c b a a (x 3)(x 3) x .x 3x 3x 9 x .x 3(x x ) 9 6 3( 5) 9 6 15 9 0 dır. Örnek: 2 x 6x 4 0 denkleminin köklerinin kareleri topla – mı kaçtır? Çözüm: 2 2 2 1 2 1 2 1 2 2 x x (x x ) 2x .x şeklinde yazabiliriz. 6 4 2 1 1 36 8 28 dir. Örnek: 2 1 2 1 2 x mx 6 0 denkleminin kökleri x ve x dir. 1 1 5 ise m kaçtır? x x 6 Çözüm: 2 1 2 1 1 2 2 1 (x ) (x ) m 1 1 x x 1 m dır. x x x .x 6 6 1 m 5 ise m 5 tir. 6 6 Örnek: 2 1 2 2 1 x 5x k 0 denkleminin kökleri x ve x dir. 3x x 11 olduğuna göre, k kaçtır? Çözüm: 2 2 1 2 1 1 2 1 2 3x 11 2 2 2 1 2 1 4 1 2 1 4 3x x 11 3x 11 x dir. b x x 5 tir. a x x 5 ise 4x 11 5 4x 16 x 4 tür. x x 5 idi. x 1 dir. c x .x k k 4 tür. a Örnek: 2 1 2 2 1 2 x mx 18 0 denkleminin kökleri x ve x dir. x 12x olduğuna göre, m kaçtır? Çözüm: 1 2 2 1 2 1 3 1 2 1 18 3 1 2.6 3.6 3 3 1 1 6 Kökler çarpımını kullanmaya çalışalım. x .x 18 dir. x 12x eşitliğinde iki tarafı da x ile çarpalım. x 12x .x olur. x 12.18 x 2.3.6.6 6 x 6 dır. x 6 değeri bu denklemin kökü ise, de 2 6 6 nklemde yerine yazabiliriz. x mx 18 0 36 6m 18 0 54 6m m 9 dur. Örnek: 2 1 2 2 1 2 x 5x 9 0 denkleminin kökleri x ve x dir. x 5x 9 kaçtır? Çözüm: www.matematikkolay.net 1 1 2 2 1 1 1 1 2 1 1 2 1 2 1 5x 9 x değeri, bu denklemin bir köküdür. Denklemde yerine yazabiliriz. x 5x 9 0 olur. x 5x 9 şeklinde de yazabiliriz. Sorulan ifade de x nin yerine 5x 9 yazalım. x 5x 9 5x 9 2 5x 9 1 2 Kökler toplamı 5 5 (x x ) 5.5 25 tir. Kökleri Verilen İkinci Dereceden Denklemi Elde Etme 1 2 2 1 2 1 2 Kökleri x ve x olan ikinci dereceden bir denklemi x (x x ) x .x 0 şeklinde yazabiliriz. Örnek: Kökleri 2 ve 3 olan ikinci dereceden bir bilinmeyenli denklemi yazınız. Çözüm: 2 2 x (2 3)x 2.3 0 x 5x 6 0 dır. Örnek: Kökleri 2 ve 2 olan ikinci dereceden bir bilinmeyenli denklemi yazınız. Çözüm: 2 2 2 x ( 2 2)x ( 2).2 0 x 0.x 4 0 x 4 0 dır. Örnek: 2 1 2 1 2 x 4x 6 0 denkleminin kökleri x ve x dir. Kökleri (x 2) ve (x 2) olan ikinci dereceden denklemi bulunuz. Çözüm: 1 2 1 2 1 2 1 2 4 1 2 1 2 1 2 6 4 x x 4 ve x .x 6 dır. Diğer denklemin kökler toplamı, (x 2) (x 2) x x 4 8 dir. Kökler çarpımı ise, (x 2).(x 2) x .x 2(x x ) 4 6 8 4 18 dir. Örnek: 1 2 2 2 1 2 1 2 Kökleri x ve x olan ikinci dereceden denklemde x x 13 ve x x 1 ise bu denklemi bulunuz. Çözüm: 2 2 2 1 2 1 2 1 2 2 1 2 1 2 1 2 2 (x x ) x x 2x .x 1 13 2x .x 12 2x .x 6 x .x dir. O halde, bu denklem x x 6 0 dır. Not: Rasyonel katsayılı ikinci dereceden bir denklemin köklerinden biri a b ise diğer kökü a b dir. Yani eşleniğidir. Örnek: Köklerinden biri 2 5 olan rasyonel katsayılı ikinci dereceden denklemi bulunuz. Çözüm: 2 Diğer kökü 2 5 tir. Kökler toplamı 2 5 2 5 4 tür. Kökler çarpımı 2 5 . 2 5 4 5 1 dir. O halde, bu denklem x 4x 1 0 dır. Not: (Kökler Karmaşık Sayı ise) Gerçek katsayılı ikinci dereceden bir denklemin köklerinden biri a bi ise diğer kökü a bi dir. Yani eşleniğidir. Örnek: www.matematikkolay.net Köklerinden biri 3 i olan rasyonel katsayılı ikinci dereceden denklemi bulunuz. Çözüm: 2 Diğer kökü 3 i dir. Kökler toplamı 3 i 3 i 6 dır. Kökler çarpımı (3 i)(3 i) 9 1 10 dur. O halde, bu denklem x 6x 10 0 dır. Not: 2 İki denklemin birer kökü eşit ise iki denklem birbirine eşitlenir, x li terimlerin yok edilmesi sağlanır. Örnek: 2 2 x 5x m 0 x 6x m 2 0 denklemlerinin birer kökleri eşit ise m kaçtır? Çözüm: 2 İki denklemi birbirine eşitleyelim. x 5x m 2 x 6x m 2 2 2 2 x 2 dir. x 2 kökü ortak köktür. Herhangi bir denklemde yerine yazarak m’ yi bulabiliriz. x 5x m 0 4 10 m 0 m 6 dır. Not: İki denklemin kökleri aynı ise katsayıları oranı eşittir. 2 2 ax bx c 0 a b c dir. dx ex f 0 d e f Örnek: 2 2 mx 9x n 4 2x 3x 5 0 denklemlerinin çözüm kümeleri aynı ise m.n kaçtır? Çözüm: 2 2 mx 9x n 4 0 2x 3x 5 0 m 9 2 3 3 n 4 tir. 5 m 6 olmalıdır. n 4 15 n 11 n 11 dir. m.n 6.( 11) 66 buluruz.

