Soru Sor sayfası kullanılarak Köklü Sayılar konusu altında Köklü denklemler ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
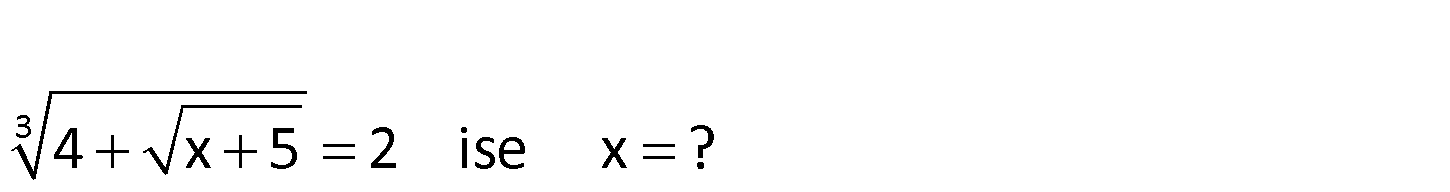
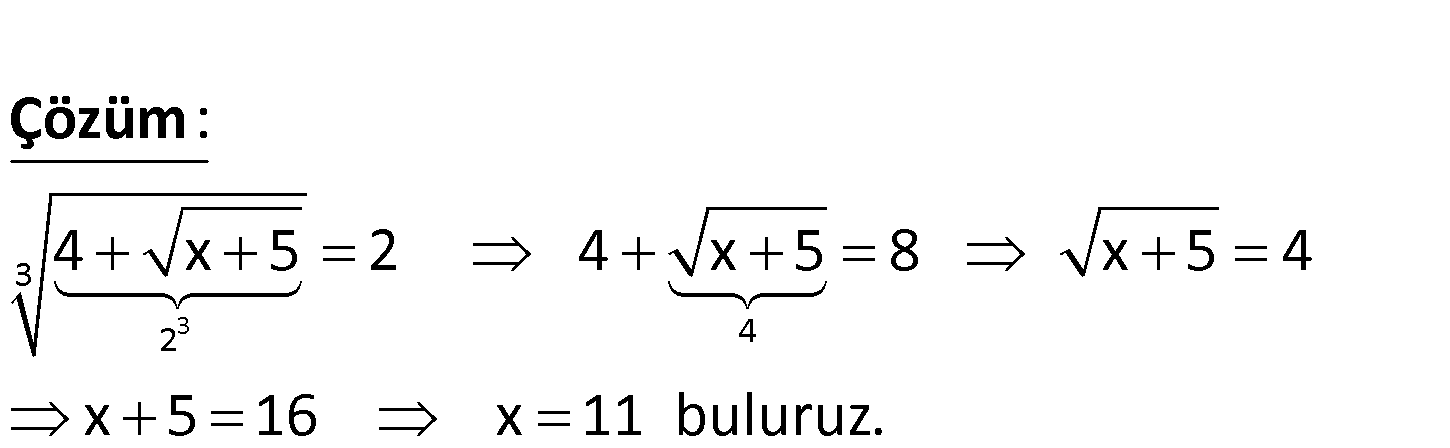
2.SORU

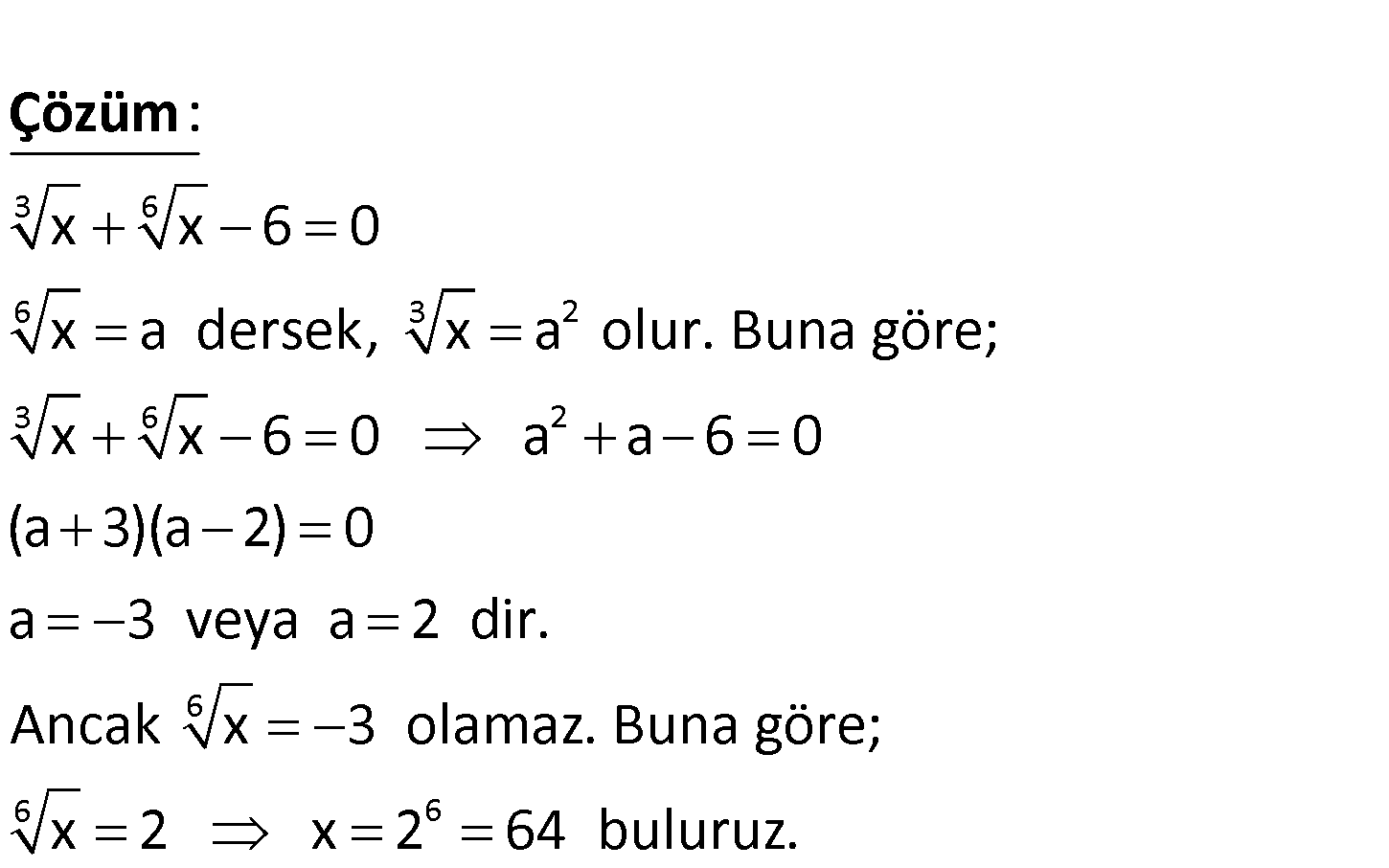
3.SORU
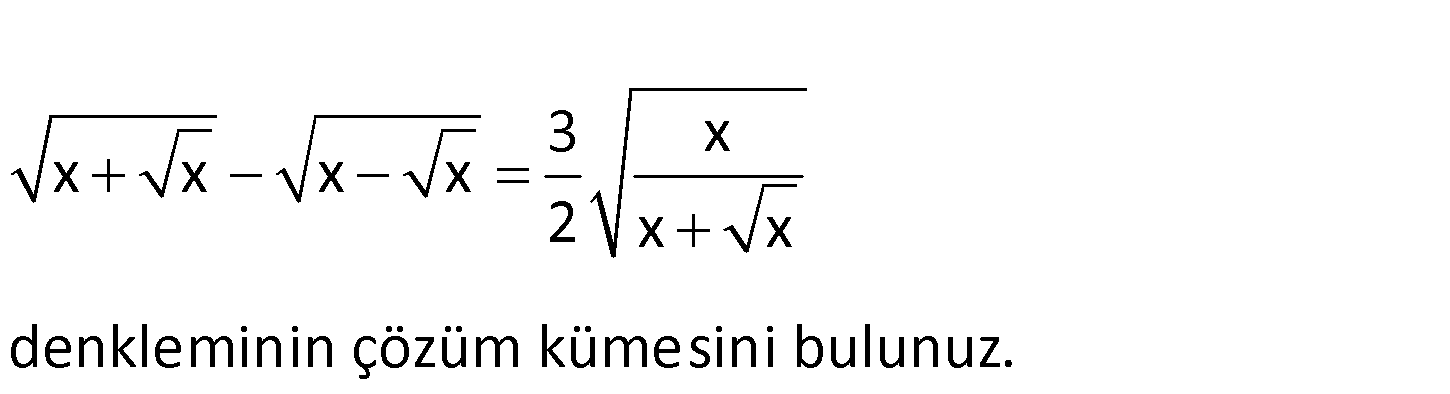
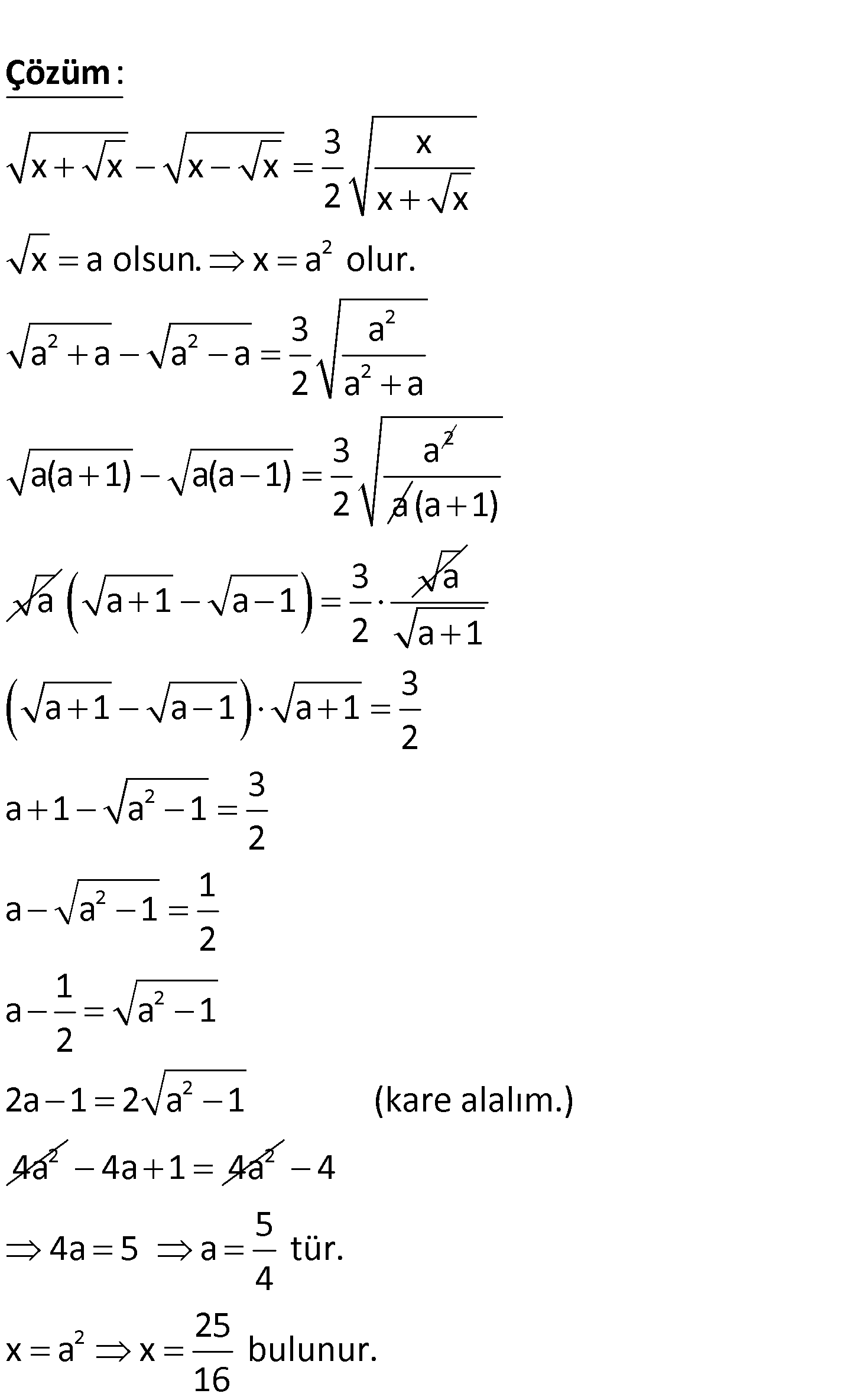
4.SORU
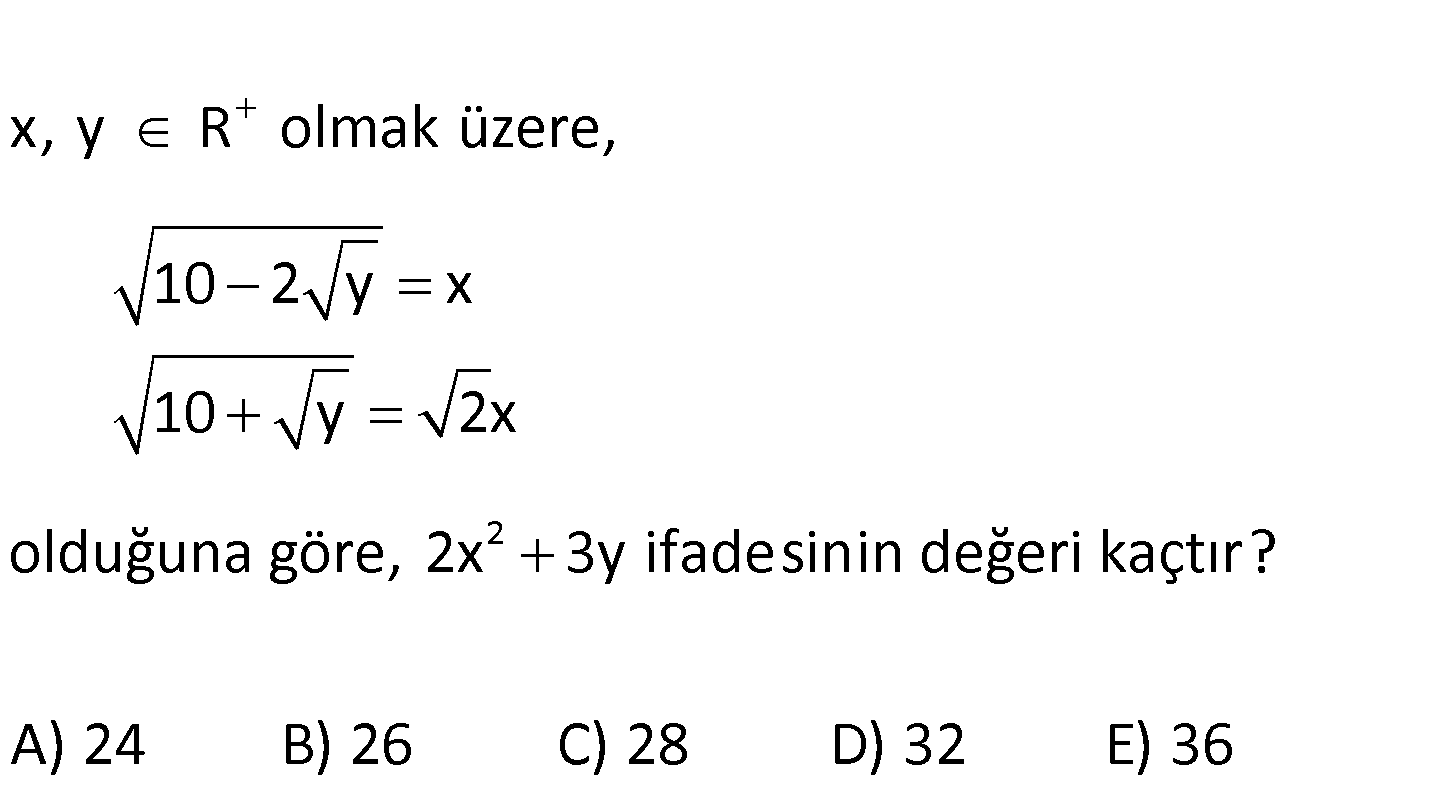

5.SORU
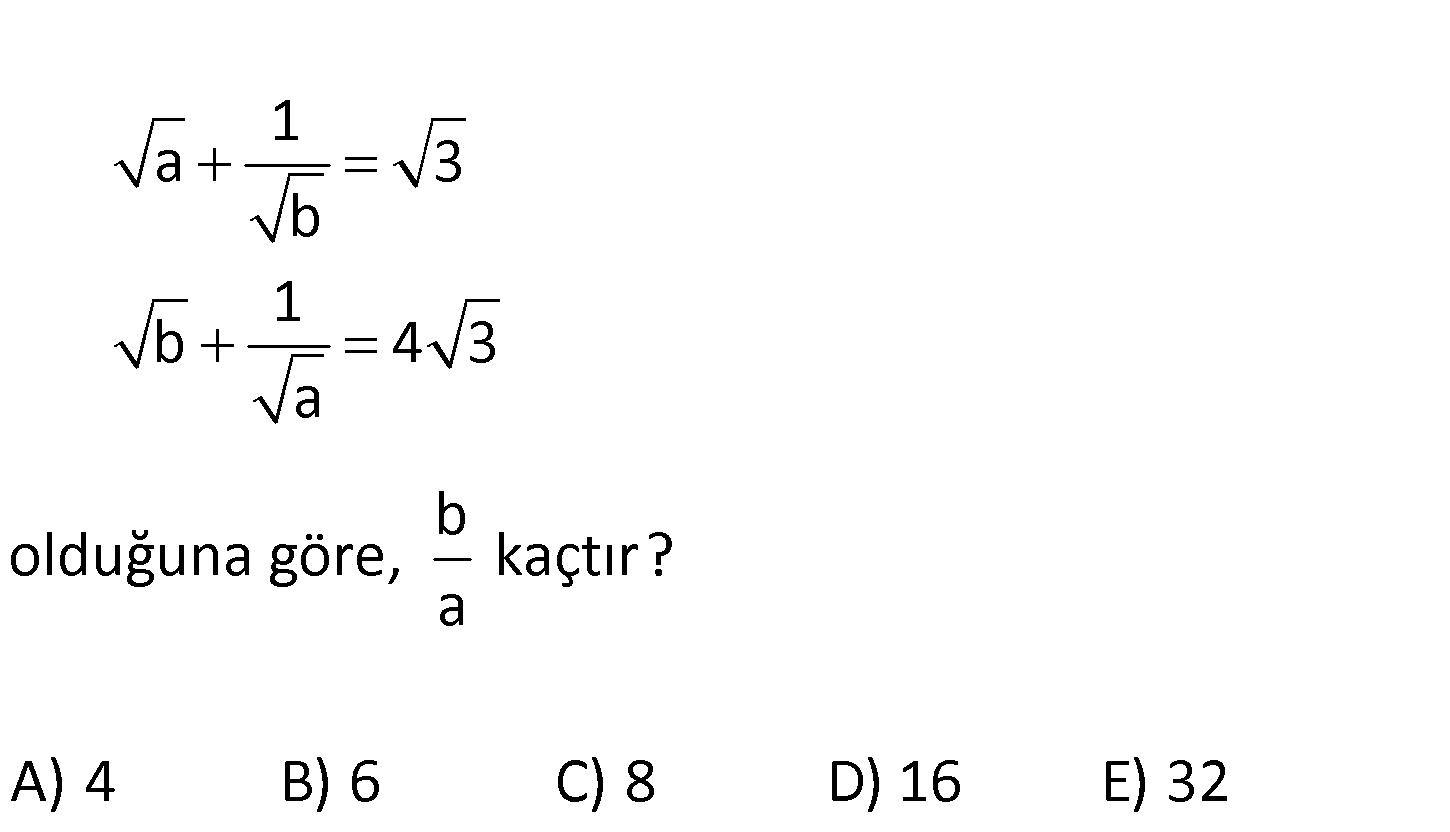
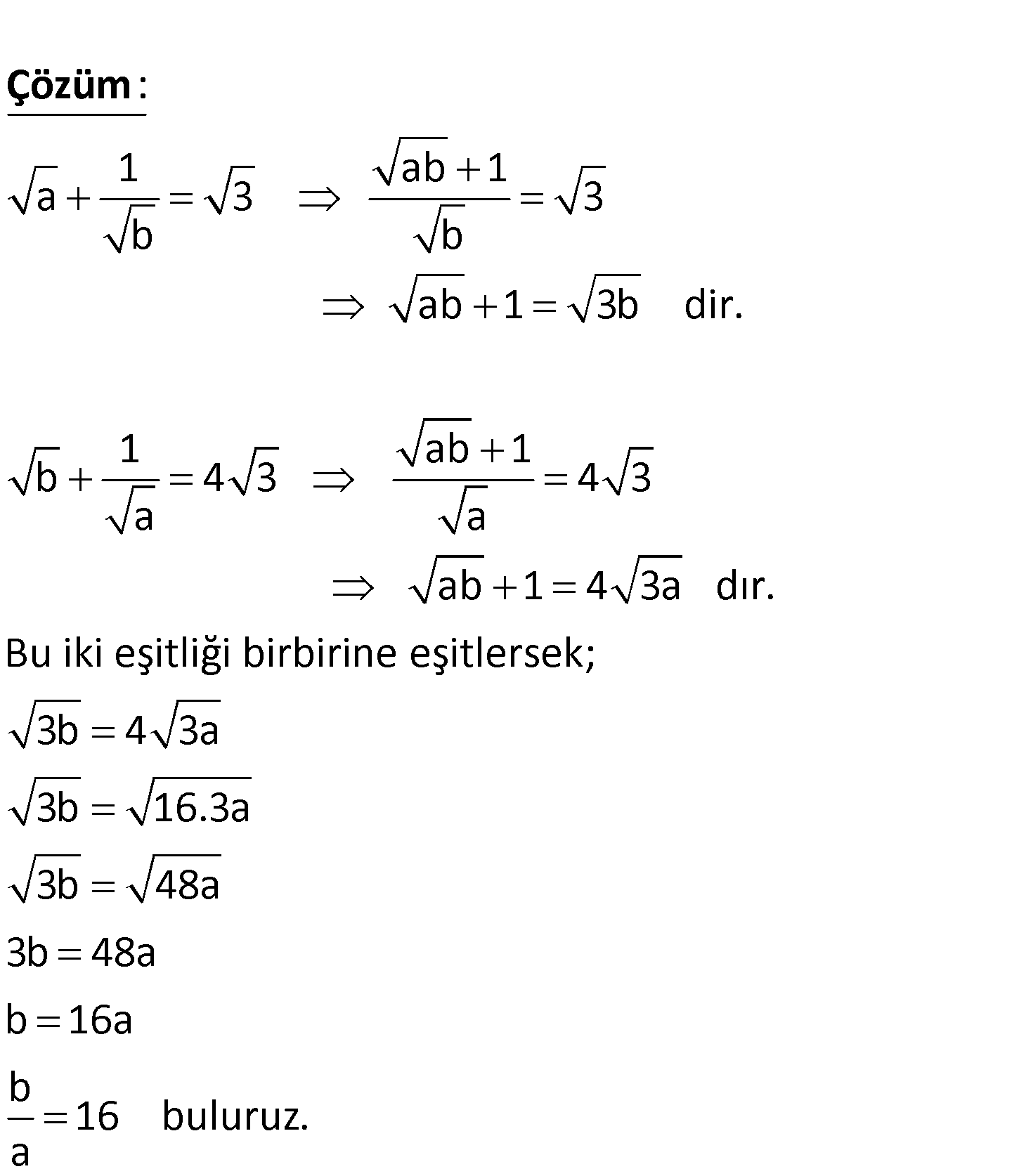
6.SORU


7.SORU

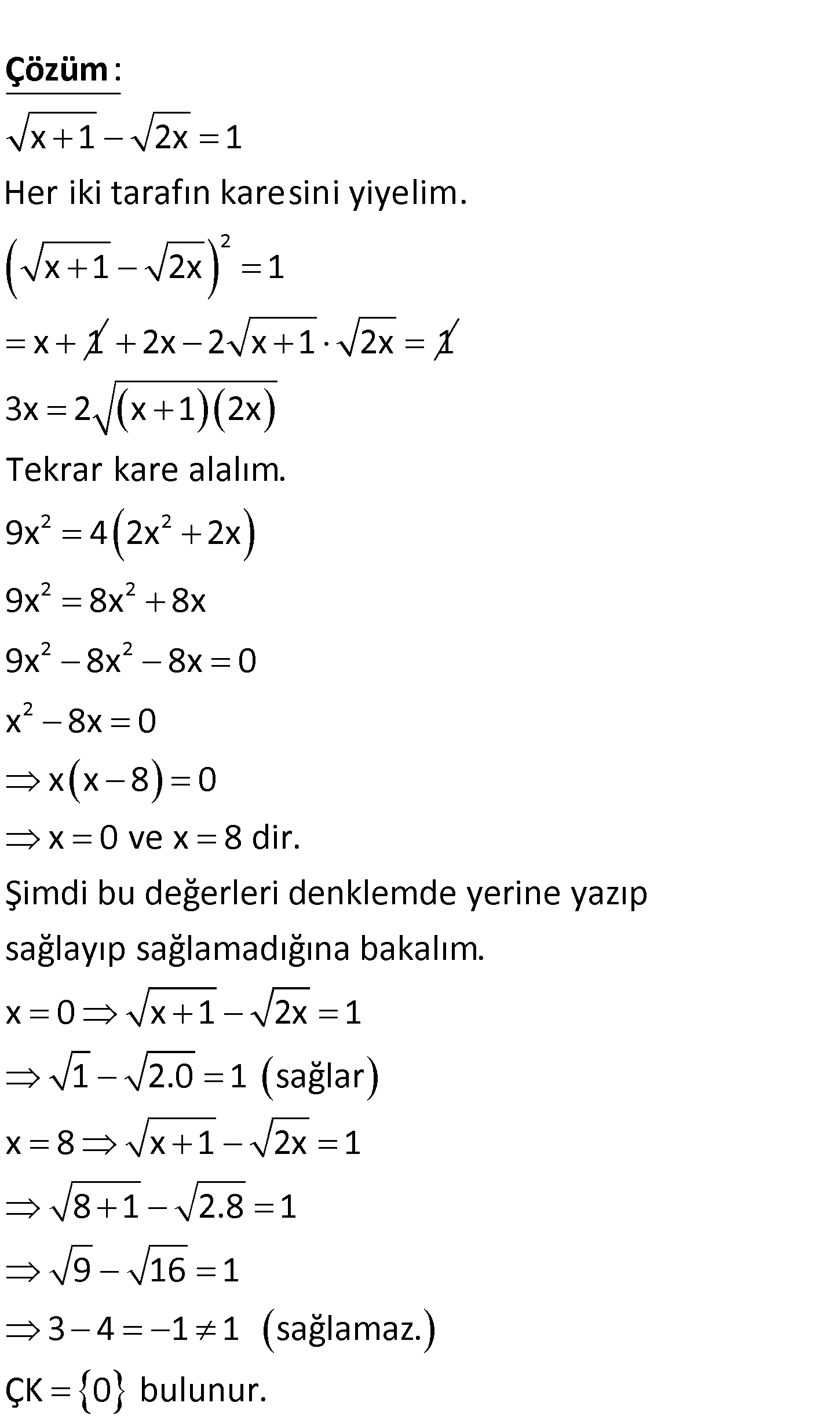
8.SORU
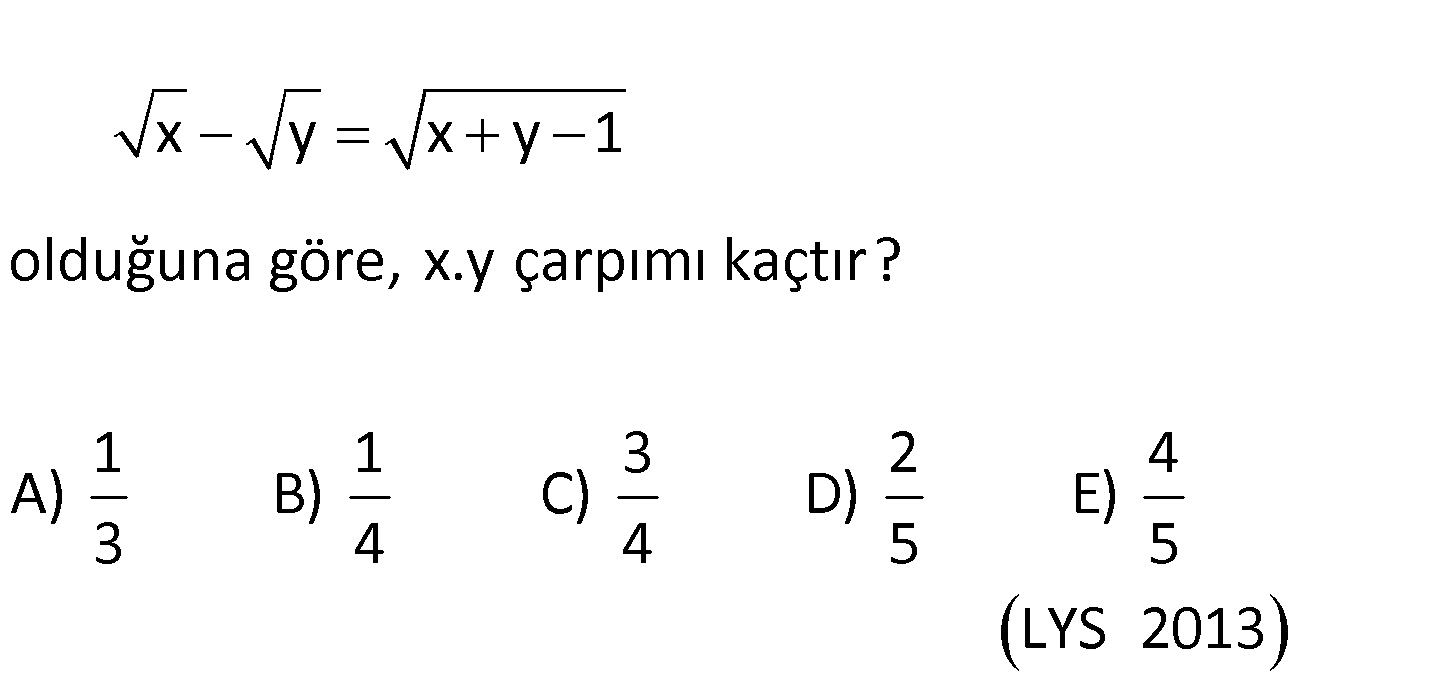
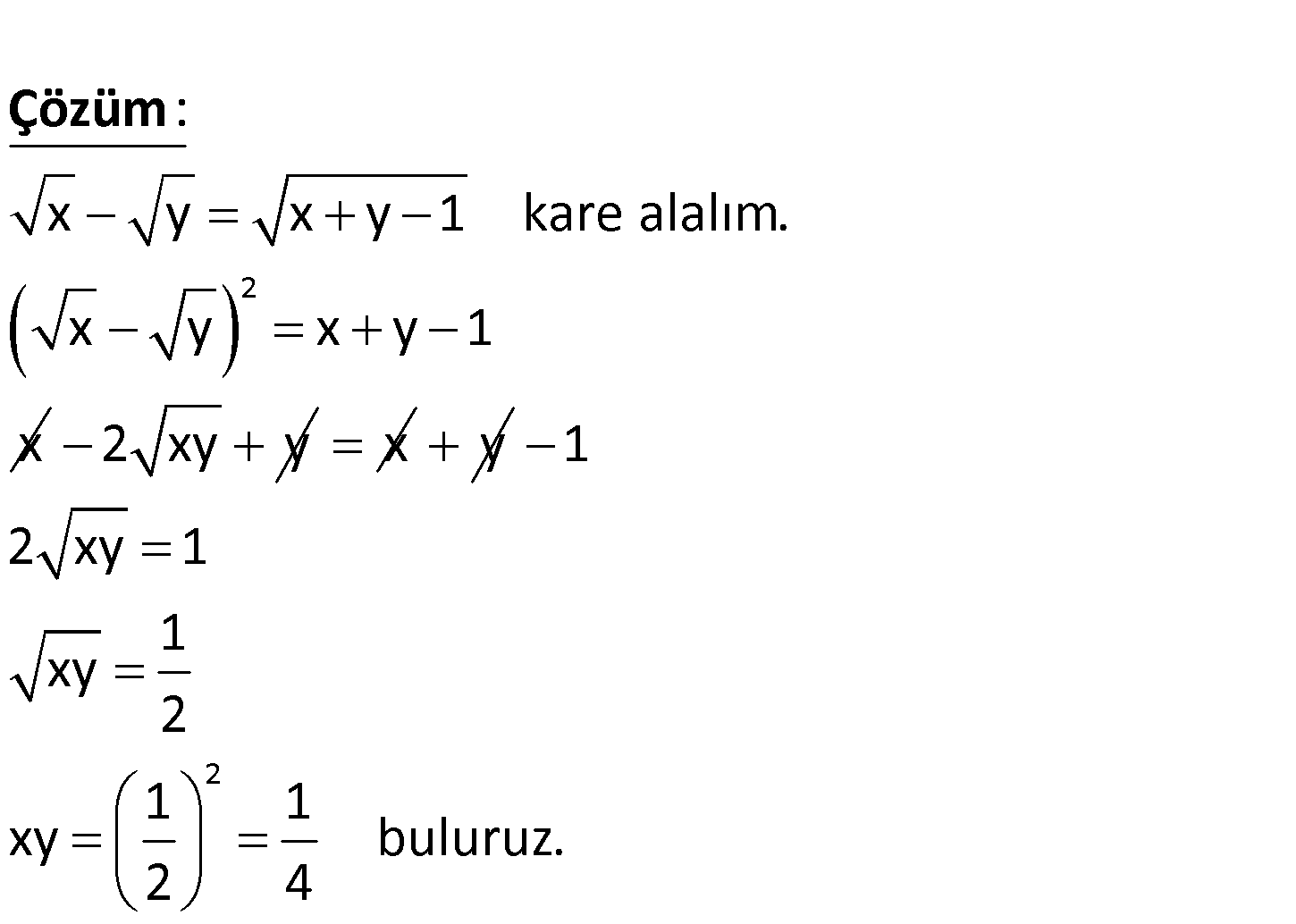
9.SORU
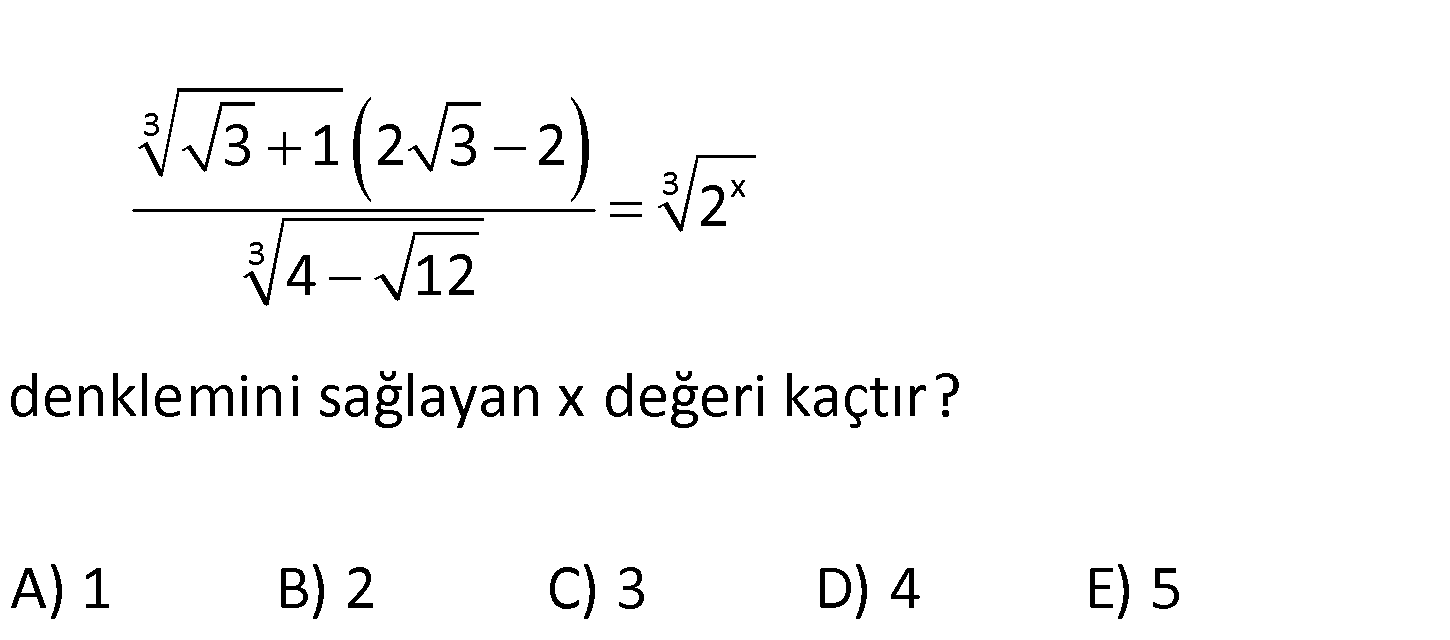
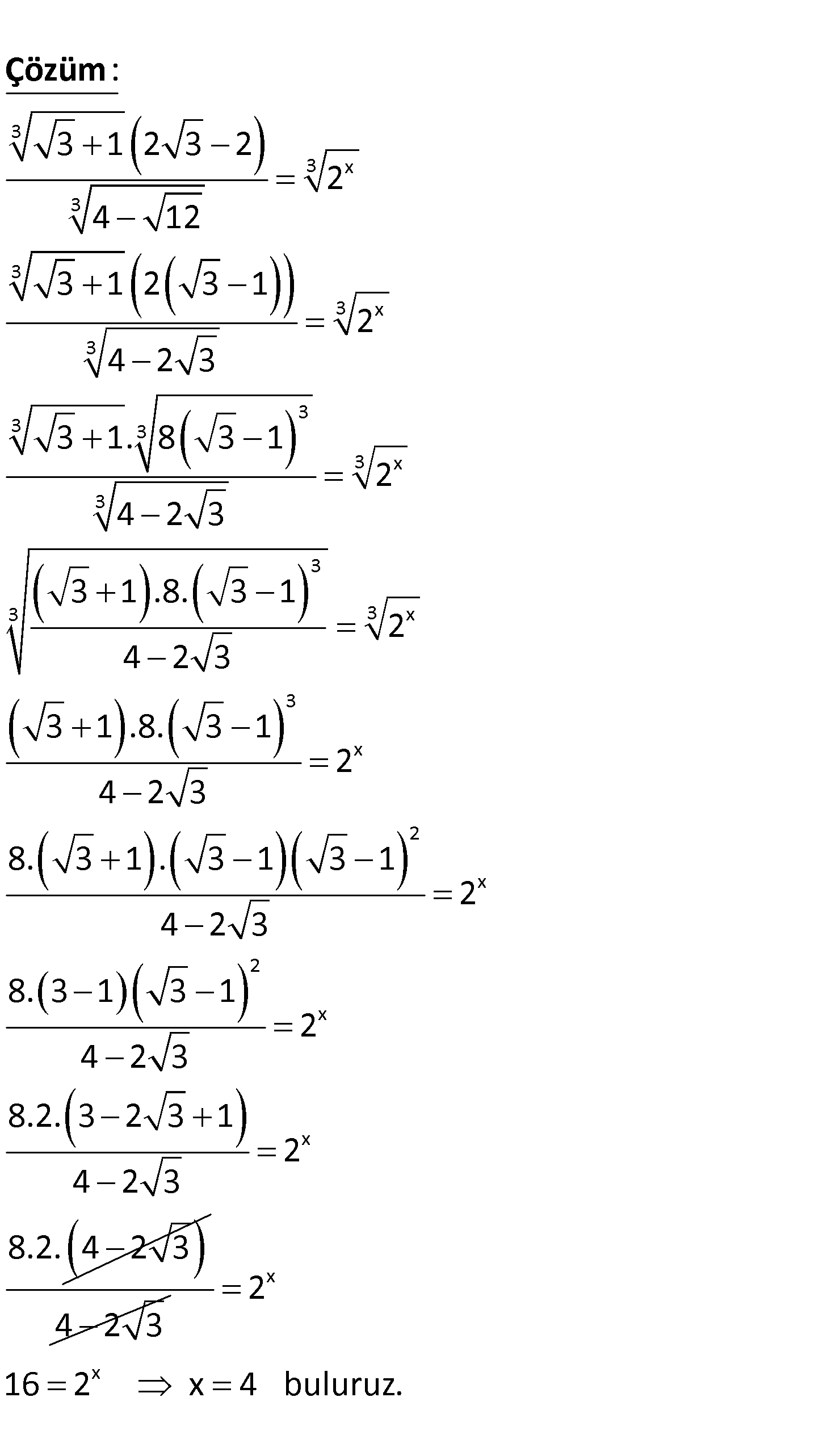
10.SORU


11.SORU
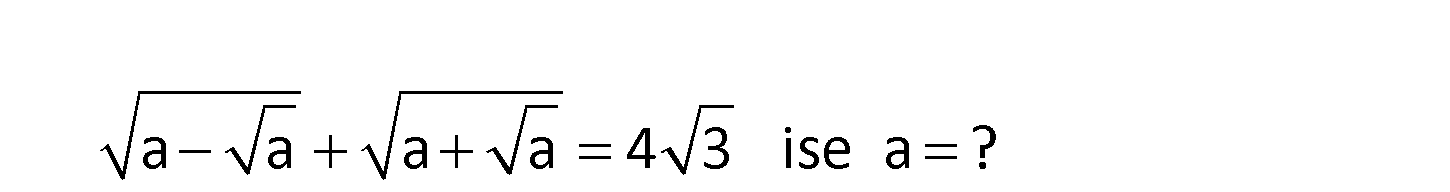

Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
3 4 x 5 2 ise x ? www.matematikkolay.net 3 3 2 4 4 x 5 2 4 x 5 8 x 5 4 x 5 16 x 11 buluruz. : Çözüm 13
3 6 x x 6 0 eşitliğini sağlayan x gerçek sayısı kaçtır? A) 1 B) 6 C) 32 D) 48 E) 64 www.matematikkolay.net 3 6 6 3 2 3 6 2 x x 6 0 x a dersek, x a olur. Buna göre; x x 6 0 a a 6 0 (a 3)(a 2) 0 a 3 veya a : Çözüm 6 6 6 2 dir. Ancak x 3 olamaz. Buna göre; x 2 x 2 64 buluruz. 31
3 x x x x x 2 x x denkleminin çözüm kümesini bulunuz. www.matematikkolay.net 2 2 2 2 2 2 3 x x x x x 2 x x x a olsun. x a olur. 3:00 AM a a a a 2 a a 3:00 AM a(a 1) a(a 1) : 2 Çözüm a(a 1) a 3 a a 1 a 1 2 2 2 2 2 2 a 1 3 a 1 a 1 a 1 2 3 a 1 a 1 2 1 a a 1 2 1 a a 1 2 2a 1 2 a 1 (kare alalım.) 4a 2 4a1 4a 2 4 5 4a 5 a tür. 4 25 x a x bulunur. 16 61
2 x, y R olmak üzere, 10 2 y x 10 y 2x olduğuna göre, 2x 3y ifadesinin değeri kaçtır? A) 24 B) 26 C) 28 D) 32 E) 36 2 2 10 2 y x 10 y 2x İki ifadenin de karelerini alalım. 10 2 y x 10 y 2x İkinci ifade ilk ifadenin ik : Çözüm 2 2 2 2 2 2 i katıdır.İlk ifadeyi 2 ile çarpıp iki ifadeyi birbirine eşitleyelim. 20 4 y 2x 10 y 2x 20 4 y 10 y 5 y 10 y 2 y 4 tür. Şimdi ifadelerden birinde y değerini yazıp x yi bulalım. 10 2 y x 10 2.2 x x 6 dı 2 r. 2x 3y 2.6 3.4 24 bulunur. www.matematikkolay.net 64
1 a 3 b 1 b 4 3 a b olduğuna göre, kaçtır? a A) 4 B) 6 C) 8 D) 16 E) 32 www.matematikkolay.net 1 ab 1 a 3 3 b b ab 1 3b dir. 1 ab 1 b 4 3 4 3 a a : Çözüm ab 1 4 3a dır. Bu iki eşitliği birbirine eşitlersek; 3b 4 3a 3b 16.3a 3b 48a 3b 48a b 16a b 16 buluruz. a 69
x 3 2 x 3 0 denklemini sağlayan x gerçek sa kaçtır? A) yılarının to 3 B) 2 C) 1 D) 1 E) 3 ı plam x 3 2 x 3 0 x 3 2 x 3 Her iki tarafın karesini alalım. : x Çözüm 32. x 32 x 2 x 2 2 2 2 1 2 9 2. 2x x 6 3x 4 x x 6 2 Her iki tarafın karesini alalım. x x 6 4 x x 2 0 x 1 x 2 0 x 1 ve x 2 dir. 1 2 1 bulunur. www.matematikkolay.net 92
x 1 2x 1 denkleminin çözüm kümesi aşağıdakilerden hangi – sidir? A) 1, 8 B) 0, 8 C) 1, 8 D) 1 E) 0 www.matematikkolay.net 2 x 1 2x 1 Her iki tarafın karesini yiyelim. x 1 2x 1 x 1 : Çözüm 2x 2 x 1 2x 1 2 2 2 2 2 2 2 3x 2 x 1 2x Tekrar kare alalım. 9x 4 2x 2x 9x 8x 8x 9x 8x 8x 0 x 8x 0 x x 8 0 x 0 ve x 8 dir. Şimdi bu değerleri denklemde yerine yazıp sağlayıp sağlamadığına bakalım. x 0 x 1 2x 1 1 2.0 1 sağlar x 8 x 1 2 x 1 8 1 2.8 1 9 16 1 3 4 1 1 sağlamaz. ÇK 0 bulunur. 110
x y x y 1 olduğuna göre, x.y çarpımı kaçtır? 1 1 3 2 4 A) B) C) D) E) 3 4 4 5 5 LYS 2013 2 x y x y 1 kare alalım. x y x y 1 x : Çözüm 2 xy y x y 2 1 2 xy 1 1 xy 2 1 1 xy buluruz. 2 4 124
3 3 x 3 3 1 2 3 2 2 4 12 denklemini sağlayan x değeri kaçtır? A) 1 B) 2 C) 3 D) 4 E) 5 www.matematikkolay.net 3 3 x 3 3 3 x 3 3 3 3 3 x 3 3 3 3 x 3 : 3 1 2 3 2 2 4 12 3 1 2 3 1 2 4 2 3 3 1. 8 3 1 2 4 2 3 3 1 .8. 3 1 2 4 2 3 3 1 .8. 3 1 4 2 3 Çözüm x 2 x 2 x x 2 8. 3 1 . 3 1 3 1 2 4 2 3 8. 3 1 3 1 2 4 2 3 8.2. 3 2 3 1 2 4 2 3 8.2. 4 2 3 4 2 3 x x 2 16 2 x 4 buluruz. www.matematikkolay.net 135
www.matematikkolay.net 3 x 3 x x denkleminin bir çözümü aşağıdakilerden hangisi – dir? 3 3 A) 6 B) 2 3 1 C) 2 D) 6 2 E) 2 2 2 2 2 2 2 3 x 3 x x (Karelerini alalım) 3 x 2 9 x 3 x x 6 2 9 x x (x a değişken : değişt Çözüm 2 irelim) 6 2 9 a a 2 9 a a 6 (Karelerinin alalım) 4.(9 a) a 12a 36 36 2 4a a 12a 36 2 2 0 a 8a a(a 8) 0 a 0 veya 8 dir. a 8 ise x 8 x 8 2 2 buluruz. 161
a a a a 4 3 ise a ? a a a a 4 3 (Karelerini alalım) a a : Çözüm 2 (a a)(a a) a a 2 2 2 48 2a 2 (a a)(a a) 48 a (a a)(a a) 24 Her tarafı 2′ ye böldük. a a a 24 a a 24 a (tekrar kare alalım) a 2 a 576 48a a 47a 576 576 a buluruz. 47 www.matematikkolay.net 26

