Soru Sor sayfası kullanılarak Köklü Sayılar konusu altında Karekökün negatif olamaması ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU
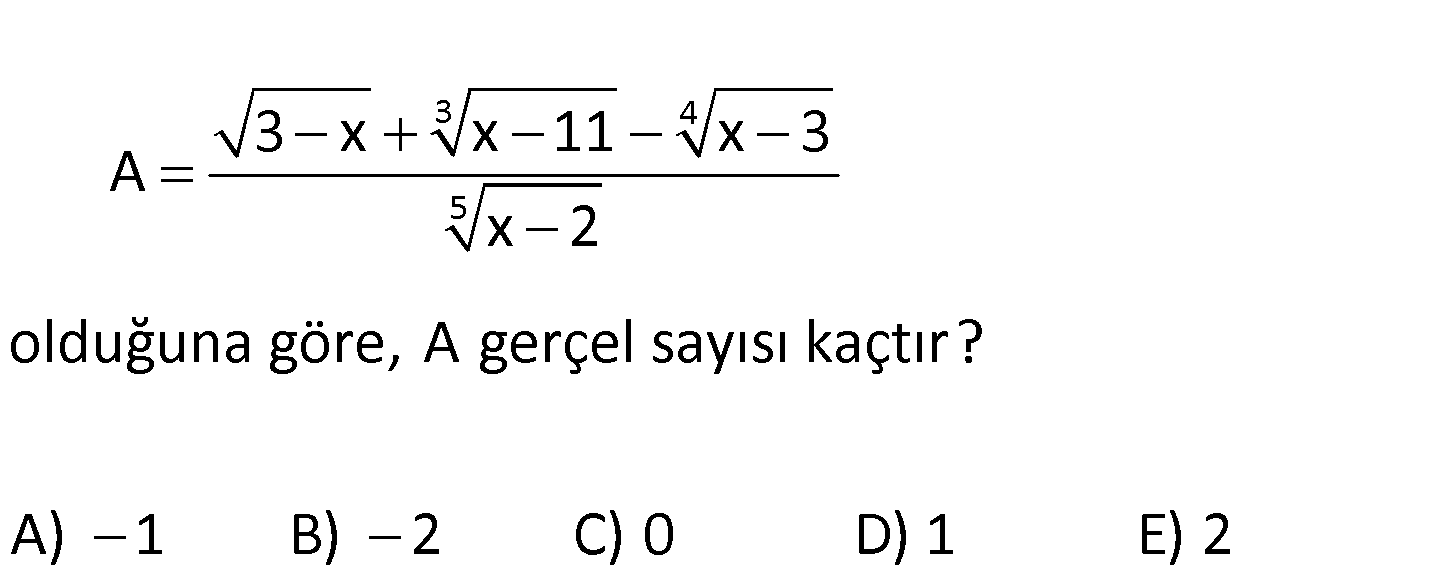

3.SORU
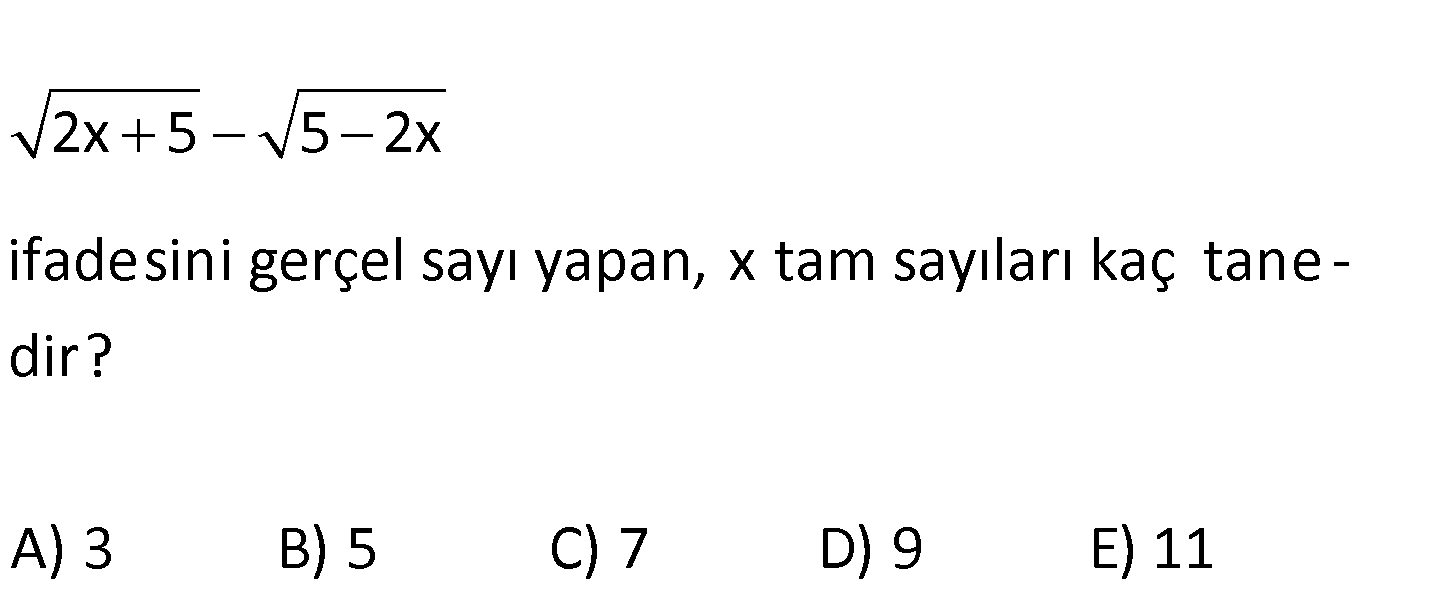

4.SORU
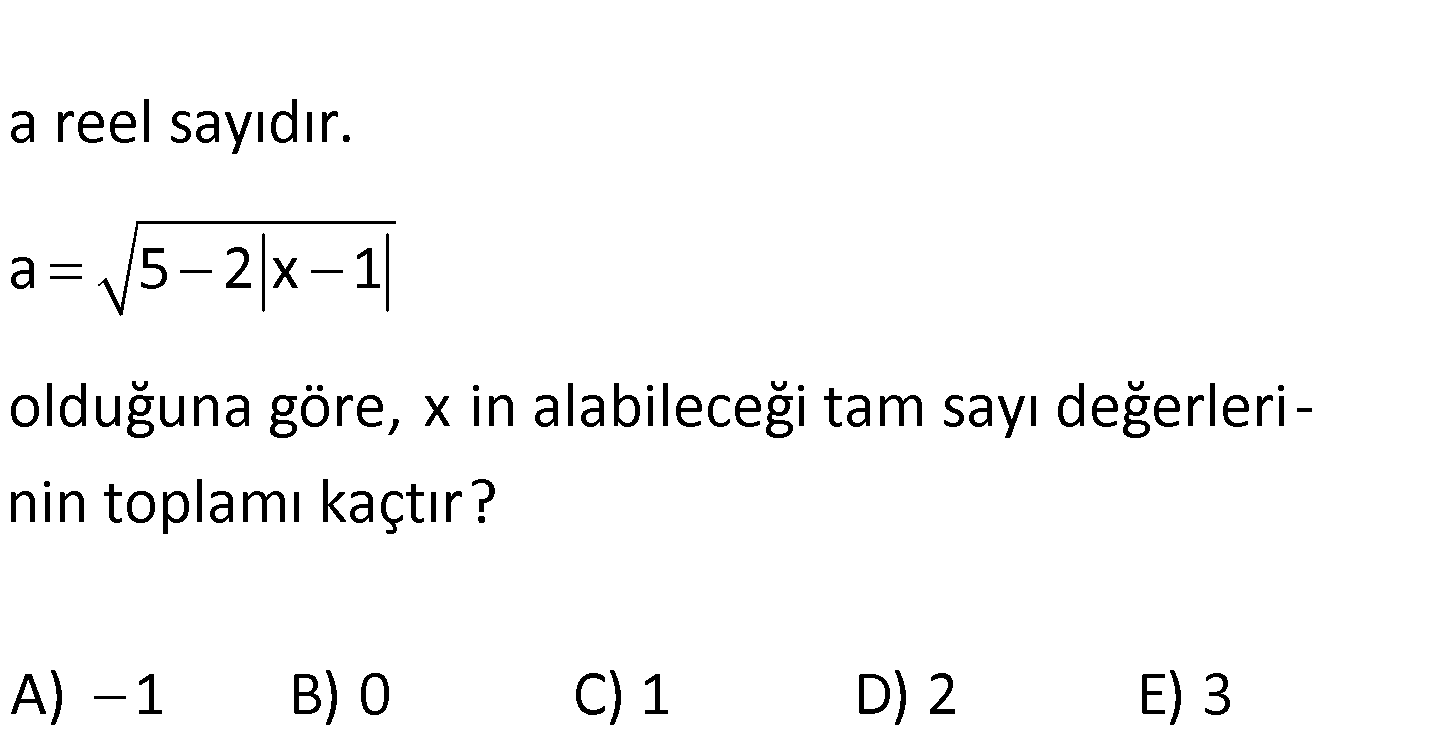

5.SORU


6.SORU
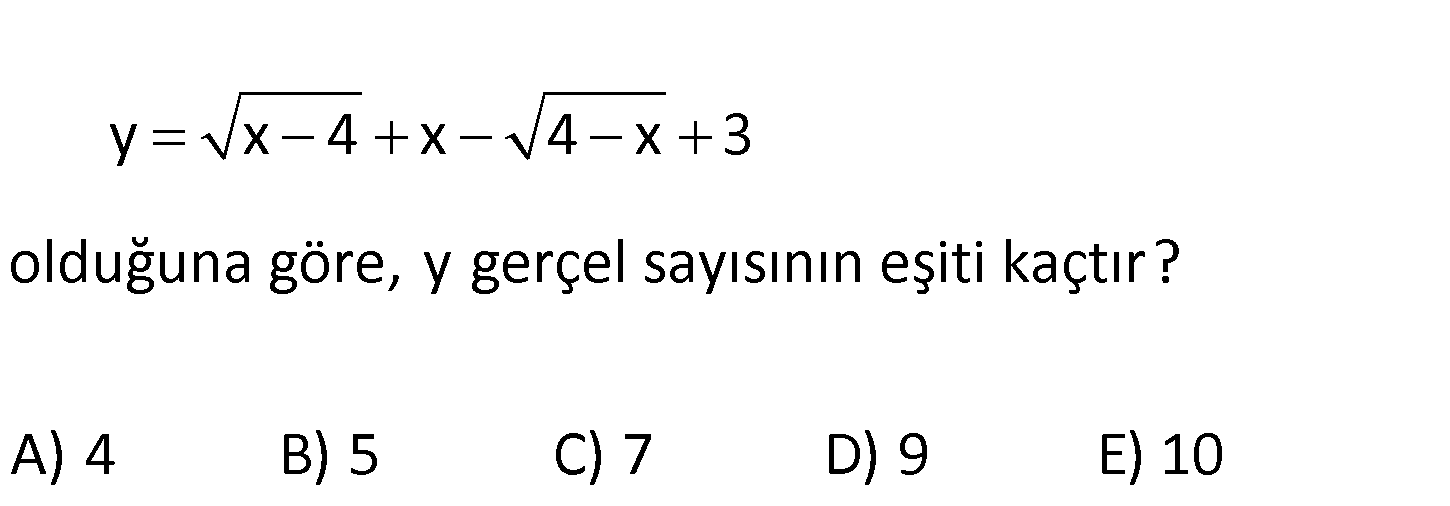

7.SORU
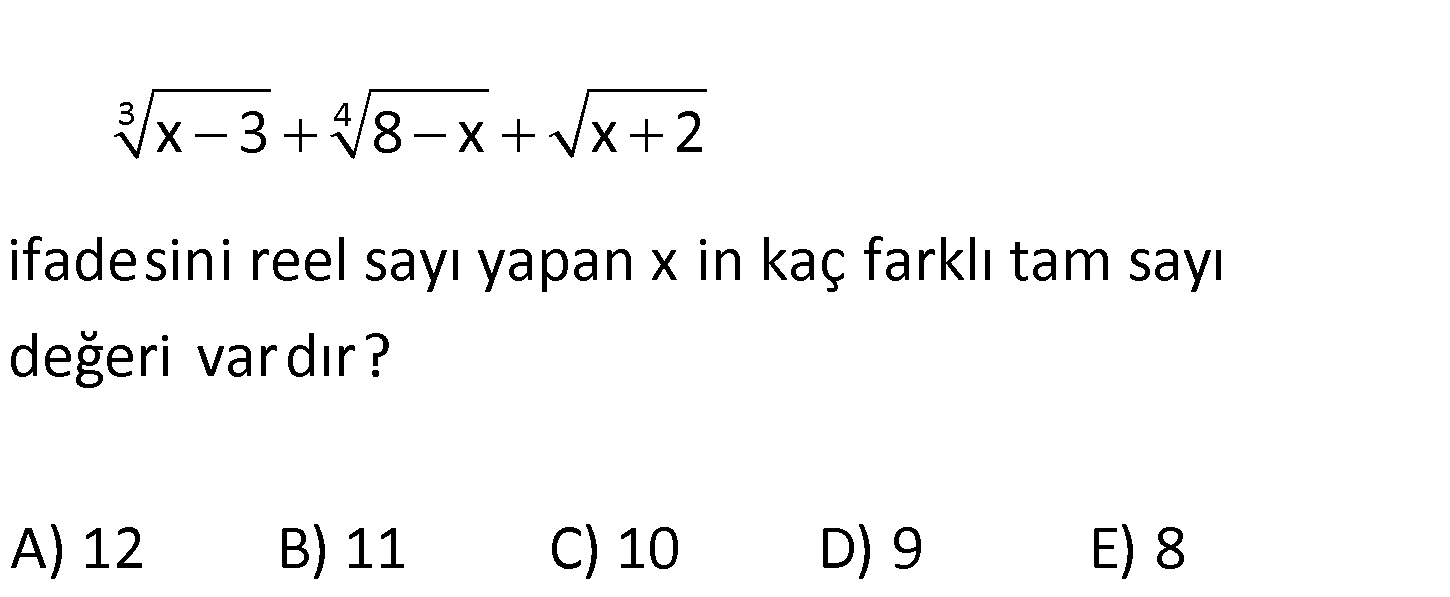

8.SORU
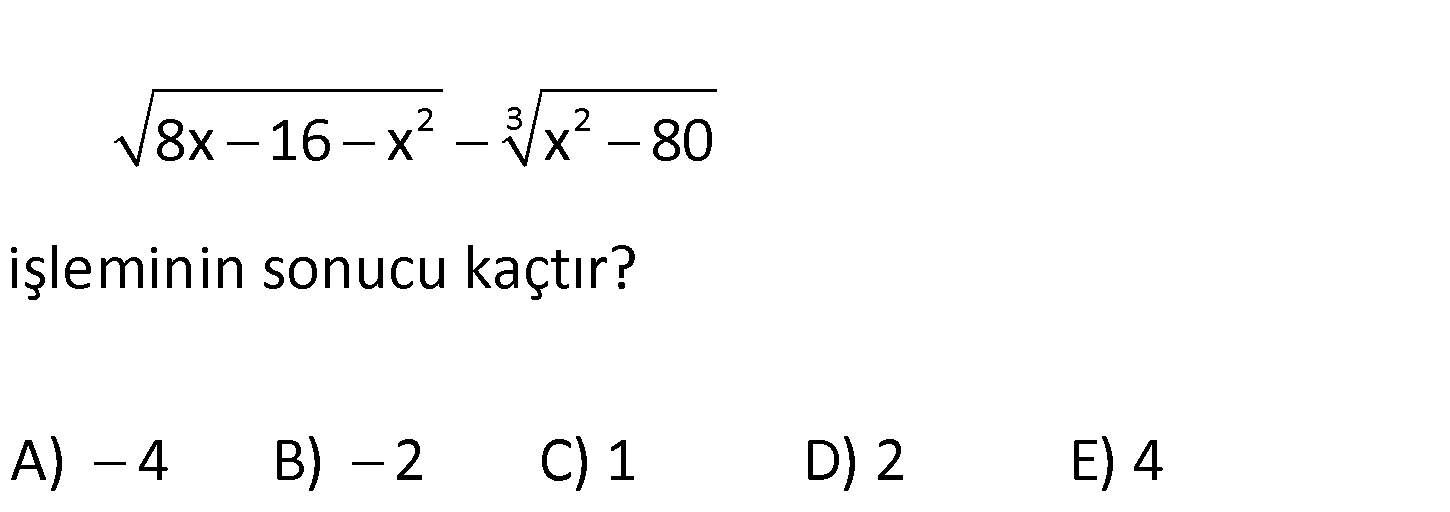

9.SORU
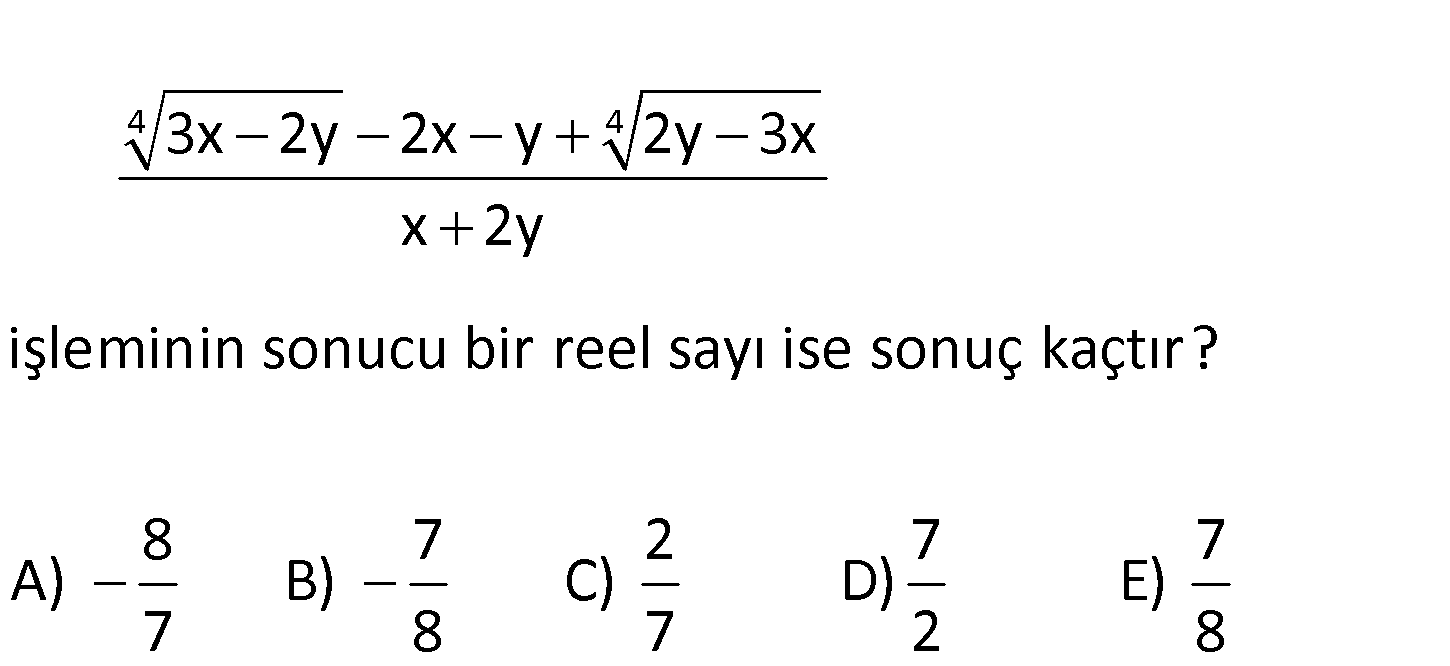

10.SORU


11.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
2 6 y 4x x 4 olduğuna göre, x y toplamı kaçtır? 2 2 2 Negatif olamaz Pozitif olamaz 6 y 4x x 4 6 y (x 4x 4) 6 y (x 2) Bu eşitliği sadece : Çözüm 0 0 sağlar. 6 y 0 y 6 x 2 0 x 2 x y 2 6 8 buluruz. 6
3 4 5 3 x x 11 x 3 A x 2 olduğuna göre, A gerçel sayısı kaçtır? A) 1 B) 2 C) 0 D) 1 E) 2 4 Çift dereceli kökün içerisi 0’dan küçük olamaz. Buna göre; 3 x 3 x 0 x 3 tür. x 3 : Çözüm 3 4 5 3 4 3 5 5 x 3 0 x 3 tür. Bu iki kıstasa göre x 3 olmak zorundadır. O halde; 3 x x 11 x 3 A x 2 3 3 3 11 3 3 0 8 0 3 2 1 2 2 buluruz. 1 10
2x 5 5 2x ifadesini gerçel sayı yapan, x tam sayıları kaç tane – dir? A) 3 B) 5 C) 7 D) 9 E) 11 www.matematikkolay.net Çift dereceli köklü ifadelerin gerçel sayı olması için kökün içerisi negatif olmamalıdır. 2x 5 : Çözüm 0 0 2,5 2,5 5 2x 5 2x 5 0 x dir. 2 5 5 2x 0 x dir. 2 Buradan; 5 5 x x { 2, 1,0,1,2} 5 tane buluruz. 2 2 33
www.matematikkolay.net a reel sayıdır. a 5 2 x 1 olduğuna göre, x in alabileceği tam sayı değerleri – nin toplamı kaçtır? A) 1 B) 0 C) 1 D) 2 E) 3 a 5 |2x 1| 0 Köklü ifadenin içi negatif olamaz. 5 |2x 1| 0 |2x 1| 5 |2x 1| : 5 5 2x 1 5 Çözüm iki tarafa da 1 ekleyelim. 4 2x 6 2 x 3 x değerleri toplamı 2 1 0 1 2 3 3 tür. 57
x bir tam sayıdır. x 5 7 x ifadesi bir gerçek reel sayı olduğu – na göre, alabileceği farklı değerler çarpımı kaçtır? x 5 7 x ifadesinin reel sayı olması için köklü ifadenin içinin negatif olmaması lazım : . x 5 0 Çözüm 5,6,7 x 5 7 x 0 7 x 5 x 7 x değerlerinin çarpımı 5.6.7 210 bulunur. 71
y x 4 x 4 x 3 olduğuna göre, y gerçel sa A yısının eşiti kaçtır? ) 4 B) 5 C) 7 D) 9 E) 10 Çift dereceli köklü ifadelerin içi negatif olamaz. x 4 x : 4 0 x 4 tür. 4 x 4 x 0 Çözüm 4 x tir. O halde, x 4 olmalıdır. y x 4 x 4 x 3 0 4 0 3 7 buluruz. 93
3 4 x 3 8 x x 2 ifadesini reel sayı yapan x in kaç farklı tam sayı değeri var dır A) 12 B) 11 ) 1 ? C 0 D) 9 E) 8 3 4 0 0 Çift dereceli köklü ifadelerin içi negatif olamaz. x 3 8 x x 2 8 x 0 8 x tir : . x Çözüm 2 0 x 2 dir. x değeri 2 den 8’e kadar tüm tam sayıları alabilir. Son Terim İlk Terim Terim Sayısı 1 Artış Miktarı 8 ( 2) Terim sayısı 1 10 1 11 dir. 1 96
www.matematikkolay.net 2 3 2 8x 16 x x 80 işleminin so A) 4 B) 2 C) nucu ka 1 D) 2 E) 4 ır? çt 2 2 2 2 İlk köklü ifadenin içine bakalım. 8x 16 x (x 8x 16) şeklinde yazabiliriz. Not : (a b) a 2 : Çözüm 2 2 2 2 (x 4) ab b Buna göre; (x 8x 16) (x 4) dir. Tam kare ifadeler pozitiftir. Bu tam kare ifadenin önünde olduğu için negatif olacaktır. Ancak çift dereceli ifadenin içi negatif olmamalıdır. O zama 2 2 3 2 3 2 3 3 n (x 4) 0 olmalıdır. Yani x 4 tür. O halde; 8x 16 x x 80 0 ( 4) 80 0 16 80 64 4 buluruz. www.matematikkolay.net 97
4 4 3x 2y 2x y 2y 3x x 2y işleminin sonucu bir reel sayı ise sonuç kaçtır? 8 7 2 7 A) B) C) D) 7 8 7 2 7 E) 8 www.matematikkolay.net 4 4 Çift dereceki köklü ifadelerin içi negatif olamaz. 3x 2y ve 2y 3x ifadelerin içi birb : i Çözüm 2k 3k 0 0 4 4 rinin tersidir.Negatif olamayacakları için ikisinin içi de 0 olmalıdır. 3x 2y 0 3x 2 y dir. 3x 2y 2x y 2y 3x 2.2k 3k x 2y 2k 2.3k 4k 3k 7k 2k 6k 7 dir. 8k 8 103
2x 1 1 ifadesinin reel sayı kalabilmesi için x 3 x yerine kaç farklı tam sayı değeri yazılabilir? www.matematikkolay.net 2x 1 1 ifadenin reel sayı olması için kökünün x 3 içinin 0 ve ya 0′ dan büyük olması g : erekir. K Çözüm x 3 esirli ifadenin de paydasının 0’dan farklı olması gerekir. x 3 0 x 3 tür. 1 2x 1 0 olmalı. 1 x 3 x 3 2x 1 0 x 3 x 2 0 x 3 x 2 0 x 3 x 2 0 işaret yön değiştirdi. x 3 x, 2 ile 3 arasında olmalı.Bunu göremedi ysek tablo çizelim. 2 3 x 2 x 3 2,3 2, 1,0,1,2 olmak üzere 5 farklı x değeri yazılabilir. 112
10 x 2 ifadesinin tanım aralığını bulunuz. www.matematikkolay.net 0 olmalı Çift dereceli köklü ifadelerin içi negatif olmamalıdır. 1.durum: : 10 x 2 x 2 Çözüm 0 olmalı 0 x 2 olmalıdır. 2.durum: 10 x 2 10 x 2 0 10 x 2 (iki tarafın karesini alalım) 100 x 2 102 x x 102 İki durumu birleştirince tanım aralığı: [2,102] bulunur. 157

