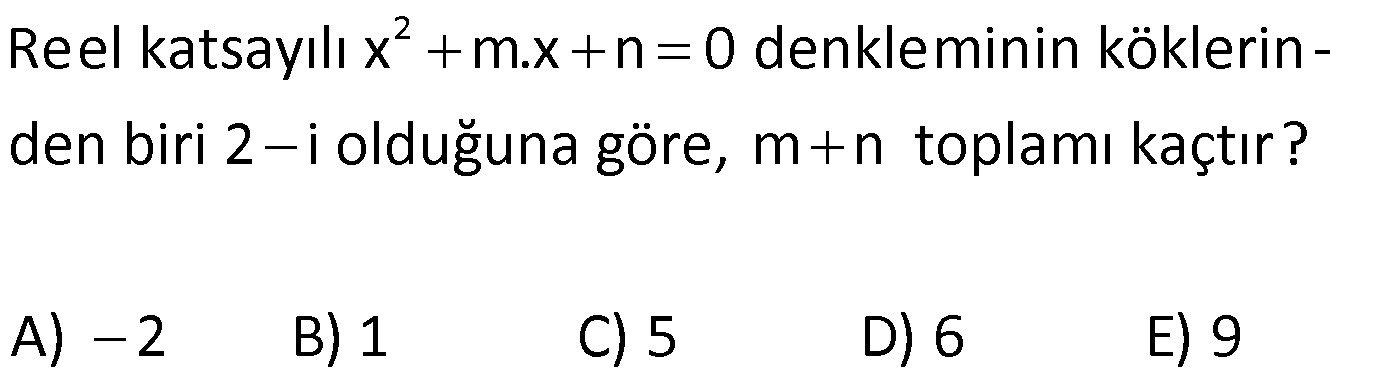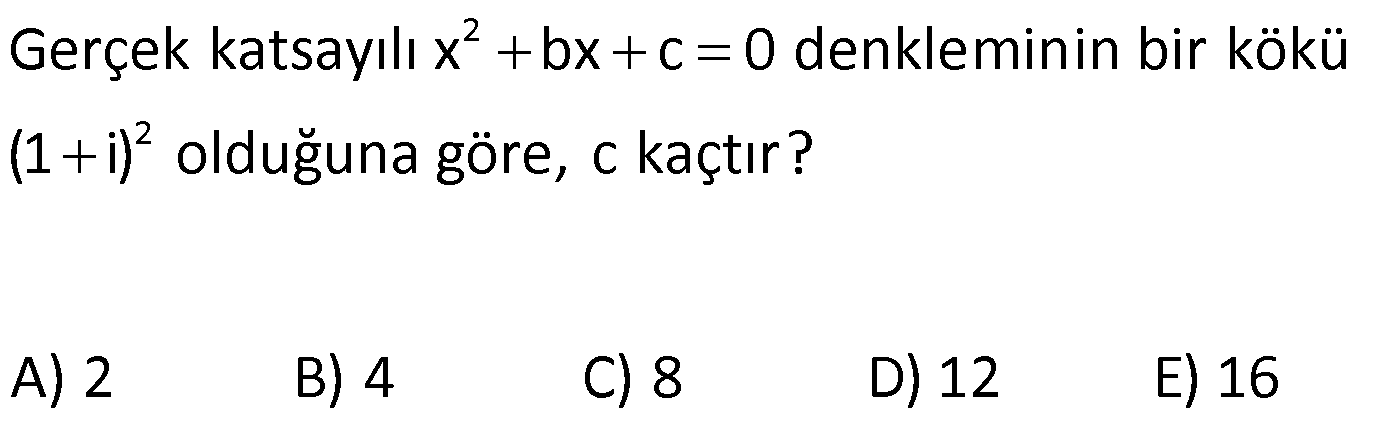Soru Sor sayfası kullanılarak Karmaşık Sayılar konusu altında Köklerden Biri Karmaşık Sayı ise ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
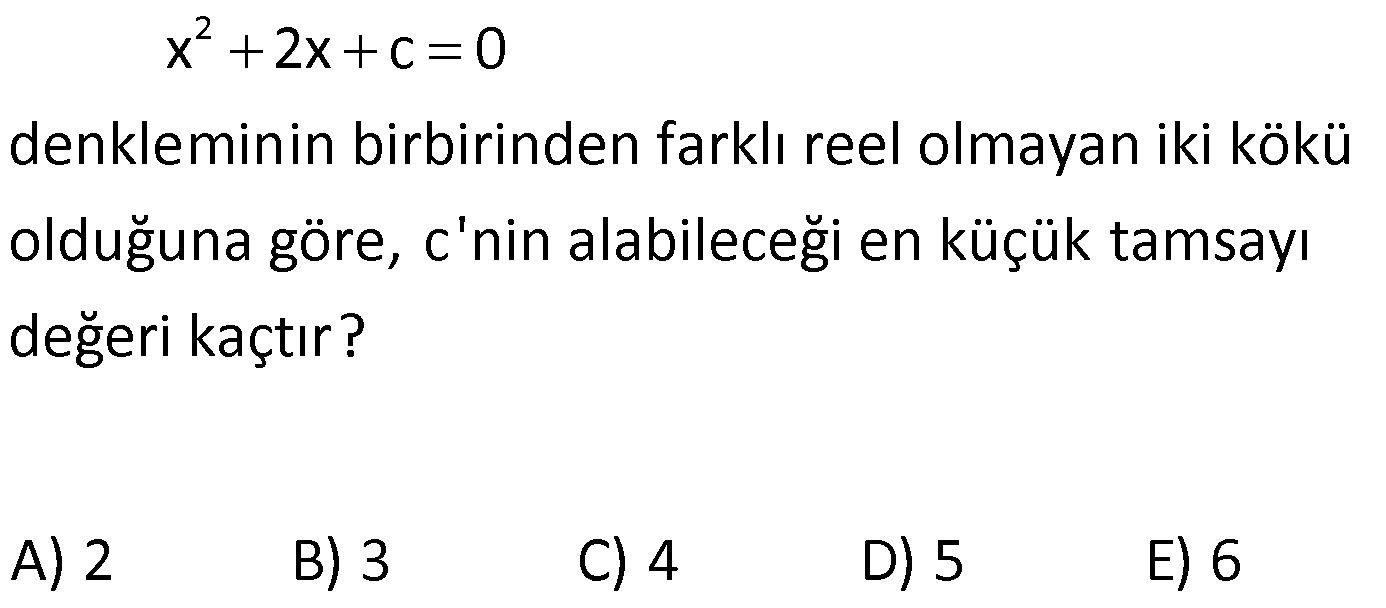
Köklerden Biri Karmaşık Sayı ise www.matematikkolay.net 1) 2 m, n R olmak üzere, 3x (m 1)x n 3 0 denkleminin köklerinden biri 1 5i olduğuna göre, m.n çarpımı kaçtır? A) 90 B) 75 C) 60 D) 45 E) 30 ÇÖZÜM: 2 2 3x (m 1)x n 0 bir kök 1 5i ise diğer kök eşleniği yani 1 5i dir. Kökler çarpımı (1 5i)(1 5i) 1 5 6 Kökler toplamı 1 5i 1 5i 2 dir. b Not : ax bx c 0 Kökler toplamı: a c Kökler çarpımı a Buna göre; n 3 Çarpımları 6 n 3 18 n 15 3 buluruz. m 1 Toplamları 2 (m 2) 6 3 m 2 6 m 4 bu luruz. m.n ( 4)(15) 60 buluruz. Cevap: C 2) 2 Reel katsayılı x m.x n 0 denkleminin köklerin – den biri 2 i olduğuna göre, m n toplamı kaçtır? A) 2 B) 1 C) 5 D) 6 E) 9 ÇÖZÜM: 2 2 x mx n 0 bir kök 2 i ise diğer kök eşleniği yani 2 i dir. Kökler çarpımı (2 i)(2 i) 4 1 5 Kökler toplamı 2 i 2 i 4 tür. b Not : ax bx c 0 Kökler toplamı: a c Kökler çarpımı a Buna göre; n Çarpımları 5 n 5 buluruz. 1 m Toplamları 4 m 4 1 Buna göre; m n 4 5 1 buluruz. Cevap: B 3) 2 2 2 2 2 i 1 olmak üzere, köklerinden biri i 4 olan reel katsayılı ikinci dereceden denklem aşağıdakilerden hangisi olabilir? A) x 4x 5 0 B) x 8x 15 0 C) x 8x 17 0 D) x 4x 17 0 2 E) x 8x 17 0 ÇÖZÜM: 2 Köklerinden biri i 4 ise diğer kök, bu köklü sayı – nın eşleniğidir. i 4 O halde kökler toplamı ( i 4) (i 4) 8 kökler çarpımı ( i 4).(i 4) 1 16 17 dir. b ax bx c denkleminde kökler toplamı, a c 2 kökler çarpımını verir. a Şıklardaki denklemlerin hepsinde a 1 olduğu için biz de a 1 diyelim. b c 8 b 8 ve 17 c 17 dir. 1 1 Buna göre denklemi x 8x 17 buluruz. Cevap: C şıkkı www.matematikkolay.net 4) 3 2 3 2 3 2 3 2 Köklerinden iki tanesi 5 ve 4 3i olan gerçek katsayı – lı üçüncü dereceden denklem aşağıdakilerden hangisi olabilir? A) x 3x 25x 25 0 B) x 13x 65x 125 0 C) x 8x 35x 45 0 D) x 12x 58x 65 0 3 2 E) x 5x 13x 45 0 ÇÖZÜM: 2 3 2 2 Köklerden biri karmaşık sayı ise diğeri onun eşleniği – dir. Yani 3.kök 4 3i dir. Buna göre denklemi yazalım; (x 5).(x (4 3i)).(x (4 3i)) 0 (x 5).(x (4 3i)).(x (4 3i)) (x 5).(x 8x 25) 0 x 8x 25x 5x 40x 3 2 125 0 x 13x 65x 125 0 buluruz. Cevap: B 5) 2 2 2 2 Köklerinden biri 3 2i olan gerçek katsayılı ikinci dereceden denklem aşağıdakilerden hangisi olabilir? A) x 6x 10 0 B) x 6x 10 0 C) x 6x 8 0 D) x 6x 8 0 E) x 2 4x 5 0 ÇÖZÜM: 2 Köklerden biri 3 i ise, diğer kök eşleniği 3 i dir. Buna göre kökler toplamı 3 i 3 i 6 Kökler çarpımı (3 i)(3 i) 10 dur. Buna göre denklemi; x 6x 10 0 buluruz. Cevap : A 6) 2 1 2 1 2 2 2 2 i 1 olmak üzere ikinci dereceden bir bilinmeyen li gerçek katsayılı bir denklemin kökleri x ve x dir. x 1 i olduğuna göre aşağıdakilerden hangisinin bir kökü x (1 i) dir. A) x x 4 0 B) x 4 0 C) x 2 2 16 0 D) x x 4 0 E) x 2x 6 0 ÇÖZÜM: 1 2 2 2 2 x 1 i eşleniği x 1 i dir. x .(1 i) ( 1 i )(1 i) 1 i i ( 1) 2i dir. Diğer kök eşleniği 2i olmalıdır. Kökler toplamı 0 Kökler çarpımı 4 tür. Buna göre denklem; x (0)x 4 x 4 bulu ruz. Cevap: B 7) 2 x 2x c 0 denkleminin birbirinden farklı reel olmayan iki kökü olduğuna göre, c’nin alabileceği en küçük tamsayı değeri kaçtır? A) 2 B) 3 C) 4 D) 5 E) 6 ÇÖZÜM: 2 Bu denklemin bir karmaşık kökü var sa, diğeri de onun eşleniği olacaktır. Otomatik olarak farklı olurlar. Başka da bir kökü olamayacağı için, gerçek kök yoktur. Gerçek kök olmaması demek, 0 demektir. b 4ac 0 4 4.1.c 0 4 4c 1 c c en az 2 olabilir. Cevap: A www.matematikkolay.net 8) 2 2 Gerçek katsayılı x bx c 0 denkleminin bir kökü (1 i) olduğuna göre, c kaçtır? A) 2 B) 4 C) 8 D) 12 E) 16 ÇÖZÜM: 2 2 2 1 x bx c 0 Denkleminin katsayıları gerçek ise kökler birbirinin eşleniği olmak zorundadır. 1 i 1 i 1 i 1 i i i 1 2i 1 2i dir. 2i kökünün eşleniği 2i dir. Denklemin 2 1 c c kökler çarpımı c dir. a 1 Köklerin çarpımı 2i 2i 4 i 4 bulunur. c 4 tür. Cevap: B