Soru Sor sayfası kullanılarak İntegral ile Alan konusu altında İki eğri arasındaki alan, Eğri ile doğru arasındaki alan ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
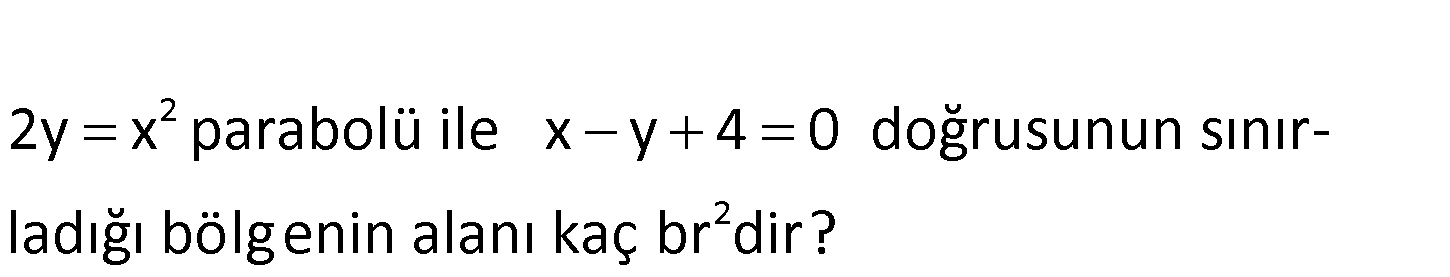

2.SORU


3.SORU

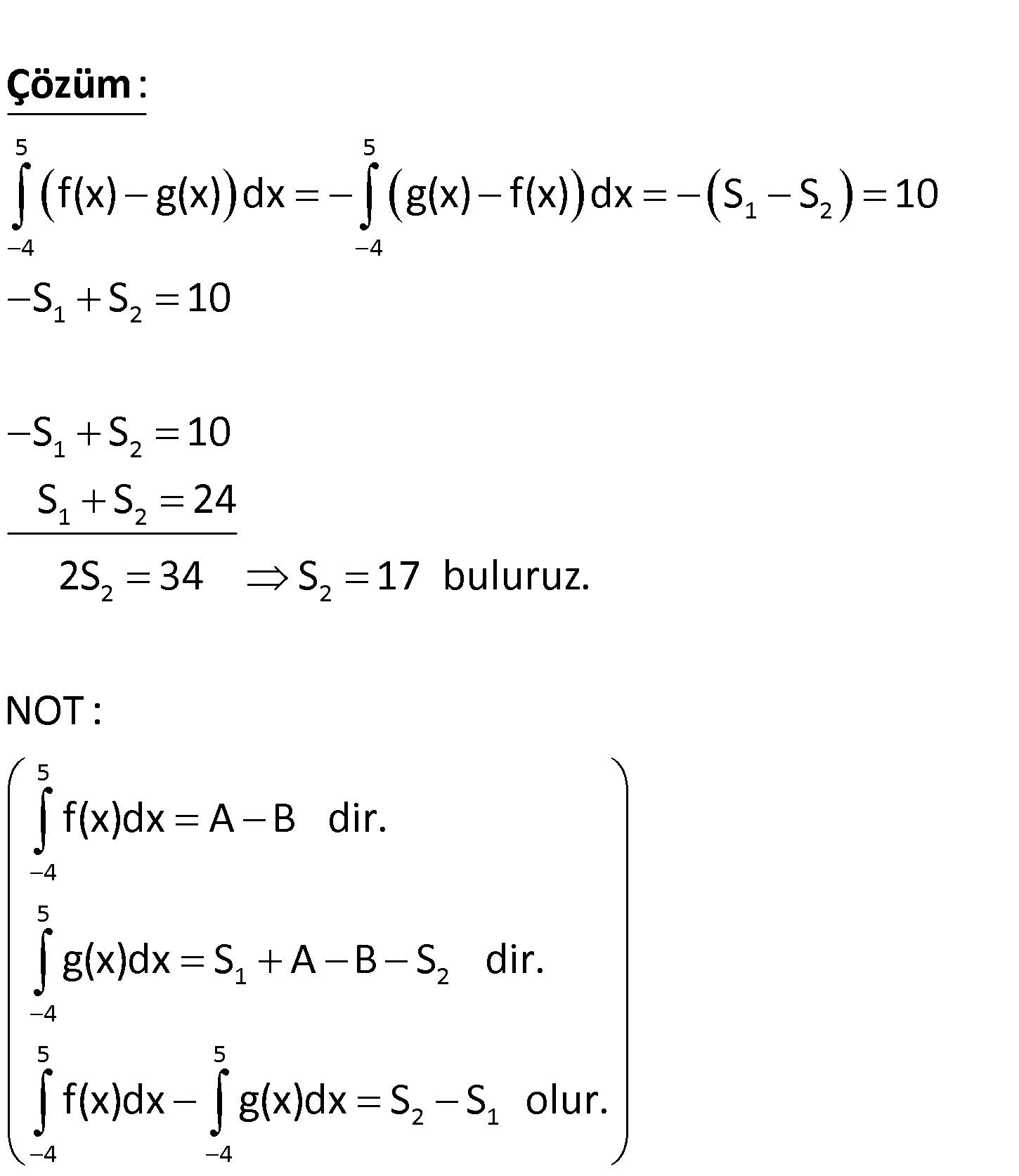
4.SORU
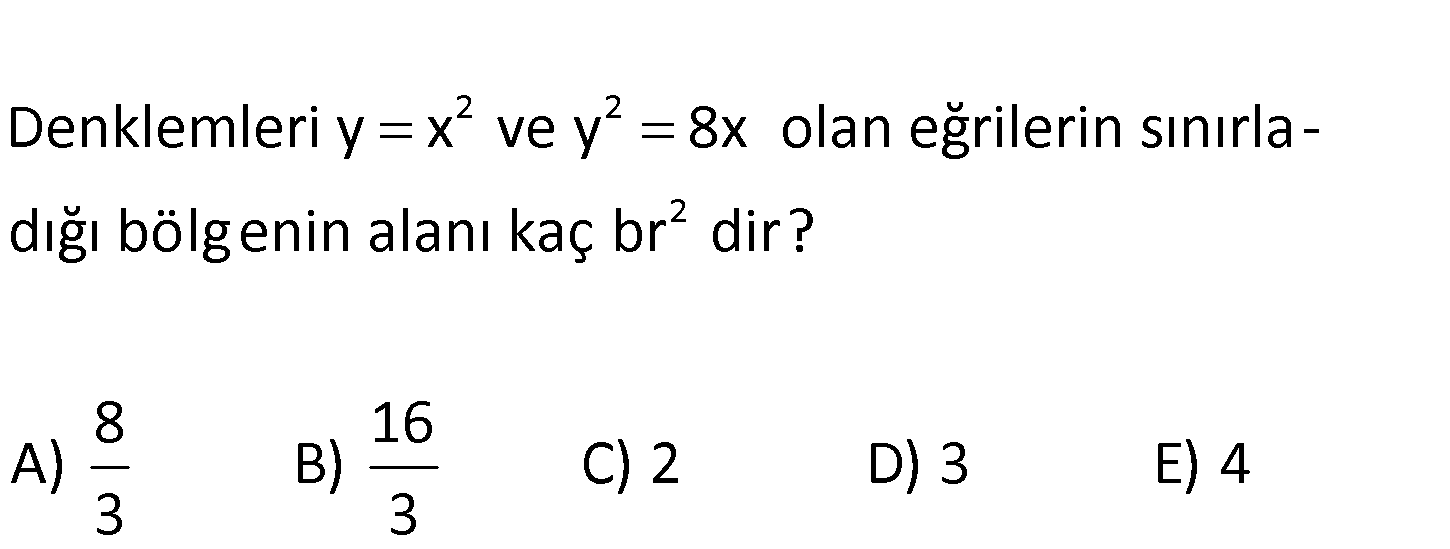

5.SORU

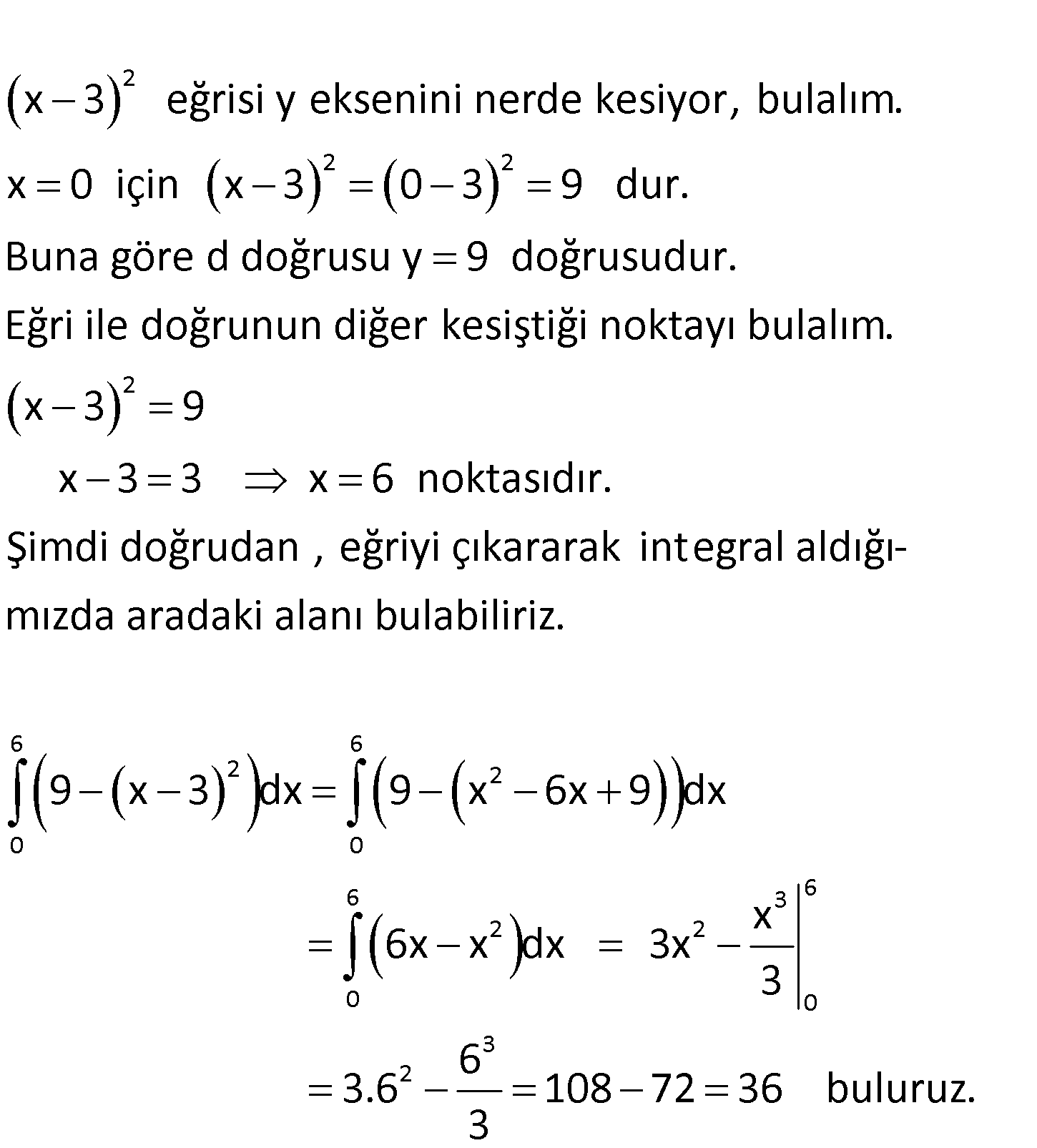
6.SORU

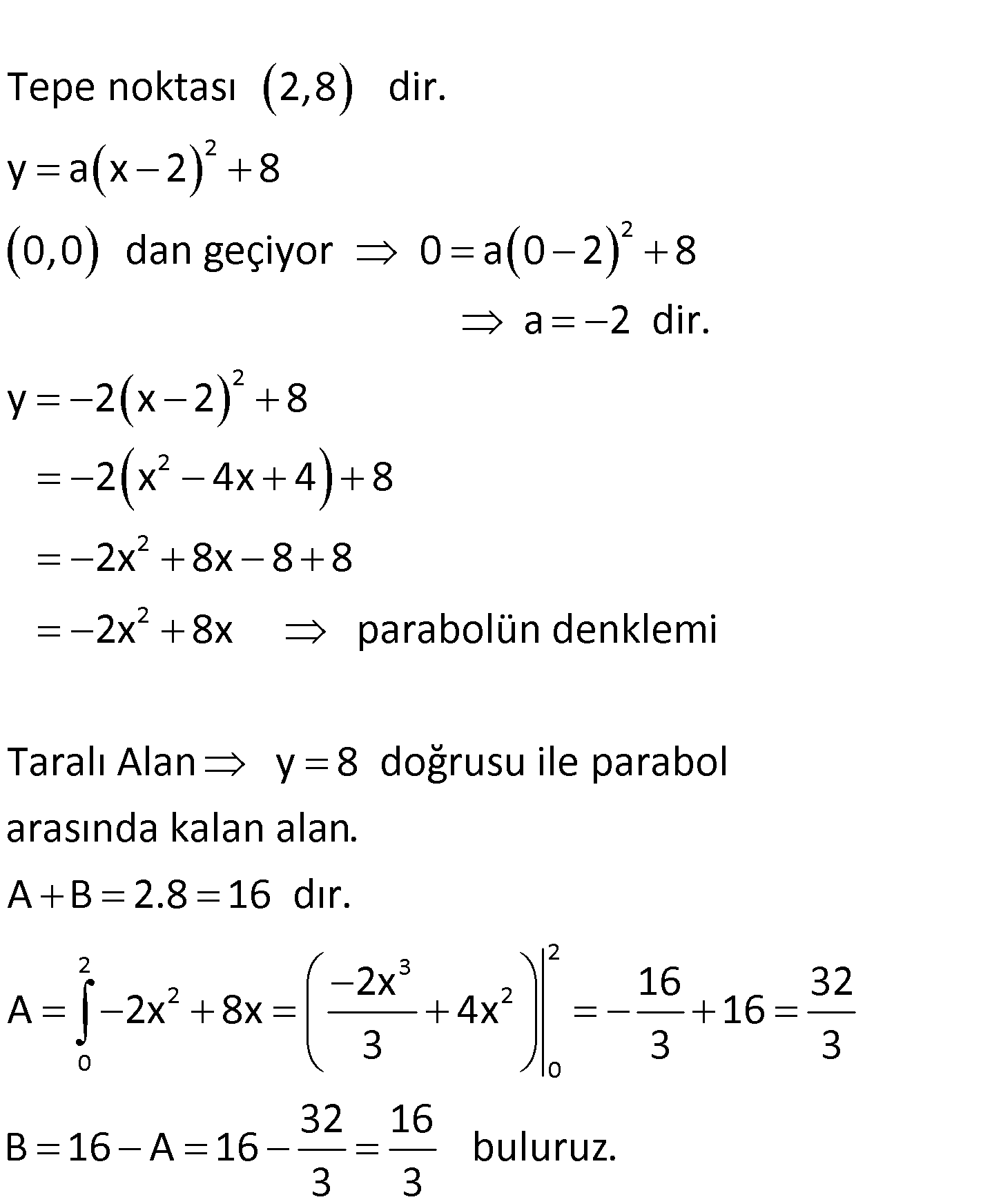
7.SORU


Burdan sonraki sorular, Fen Lisesi Müfredatı için geçerlidir.
8.SORU

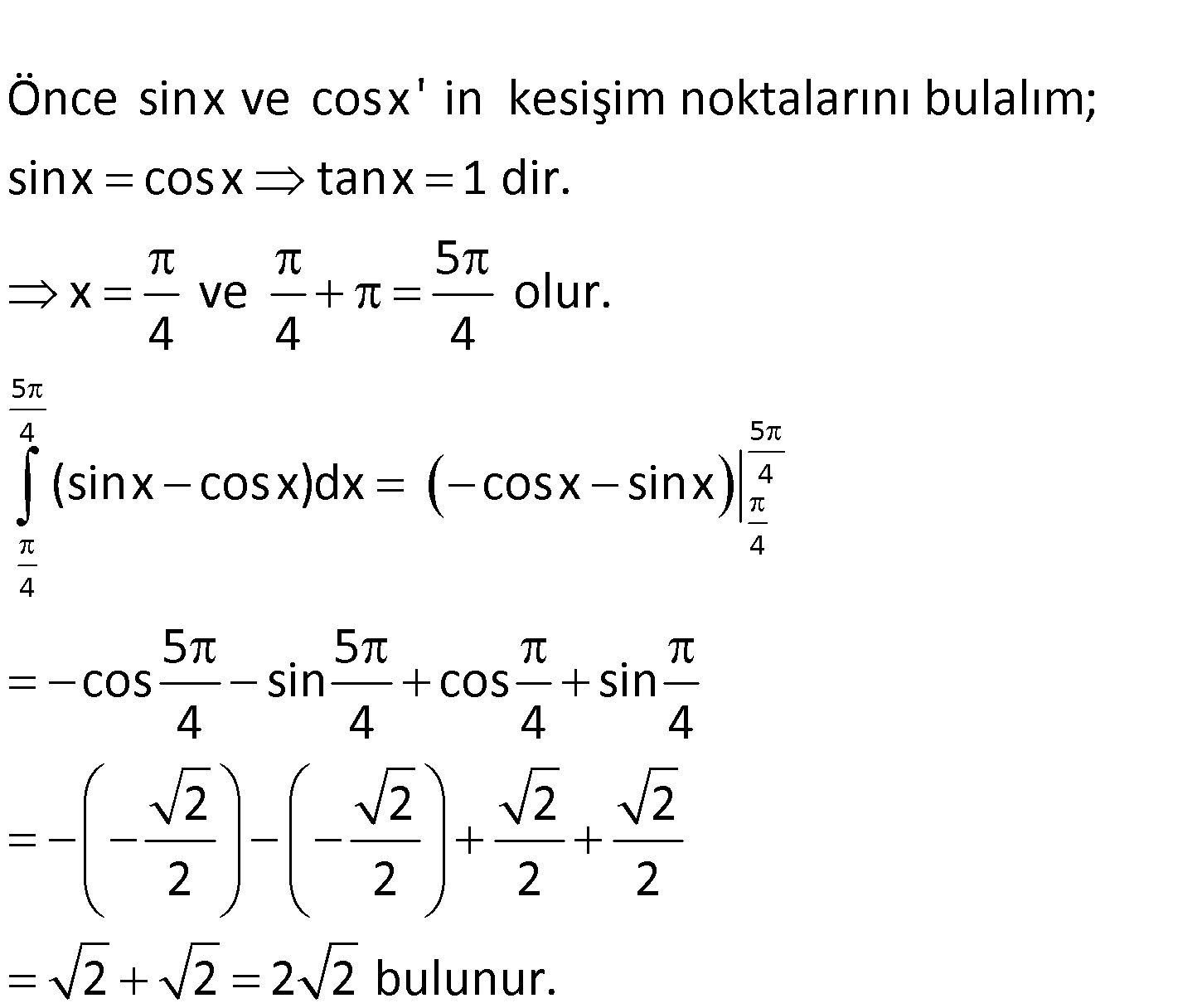
9.SORU

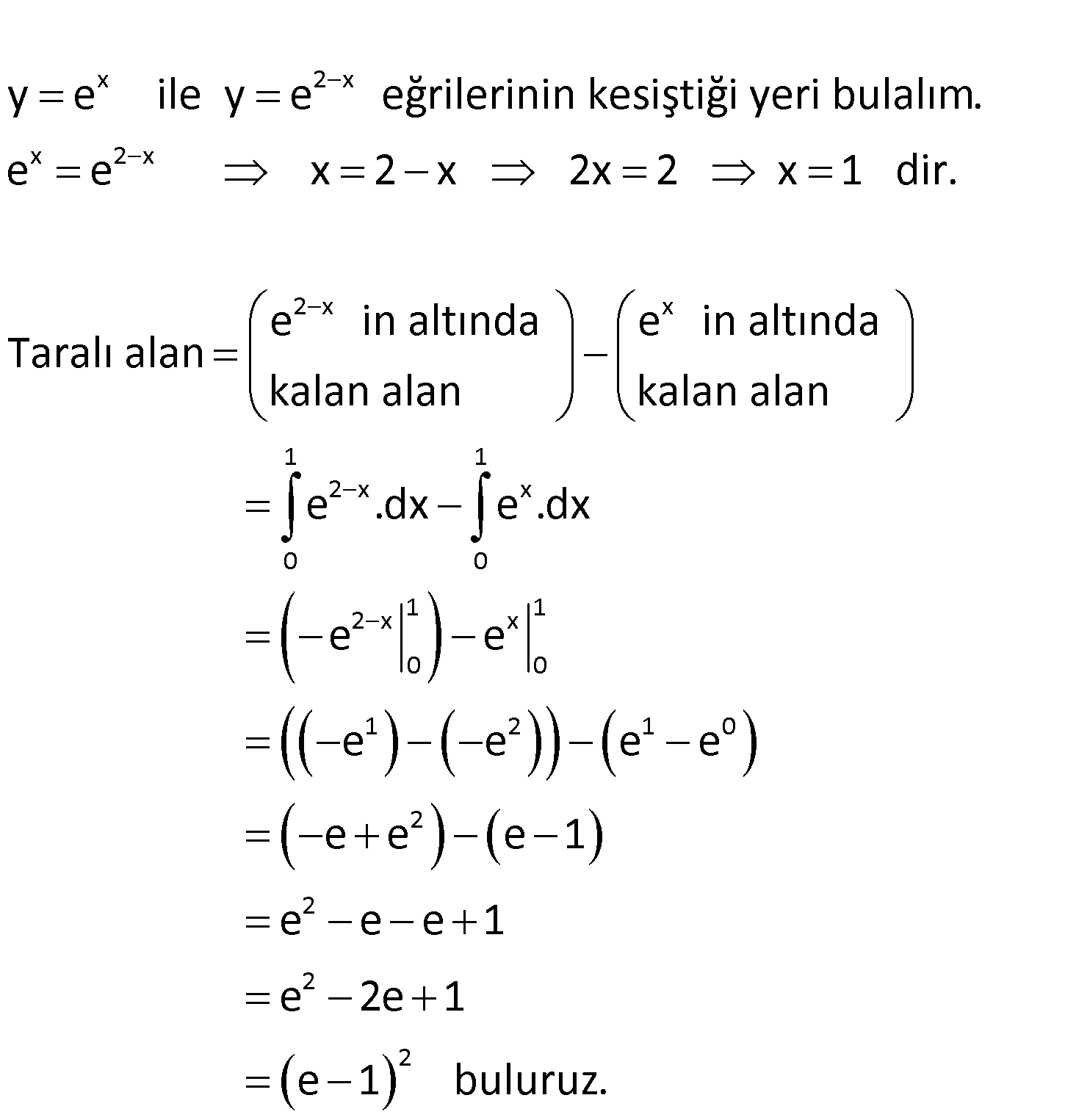
10.SORU

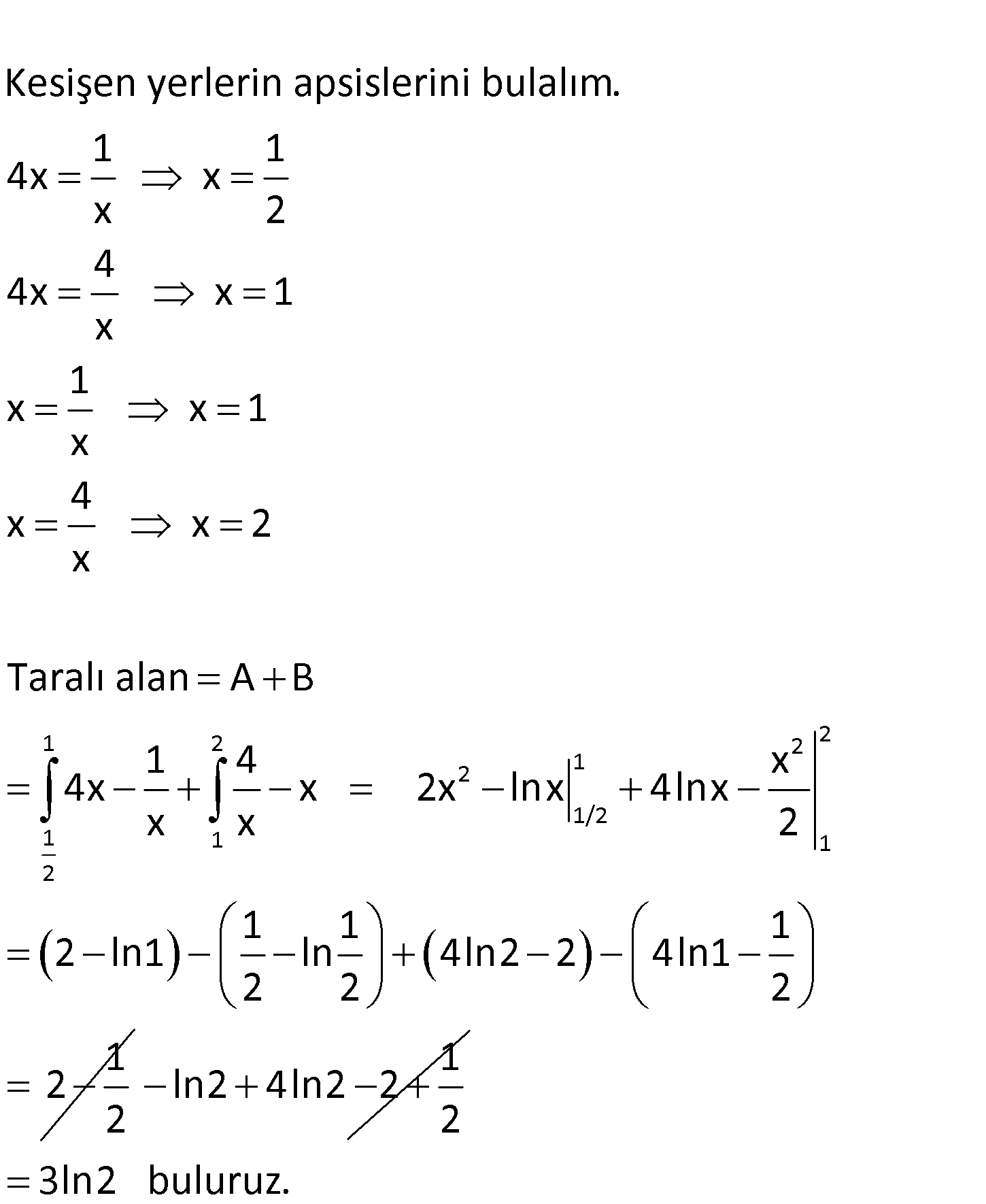
11.SORU


Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
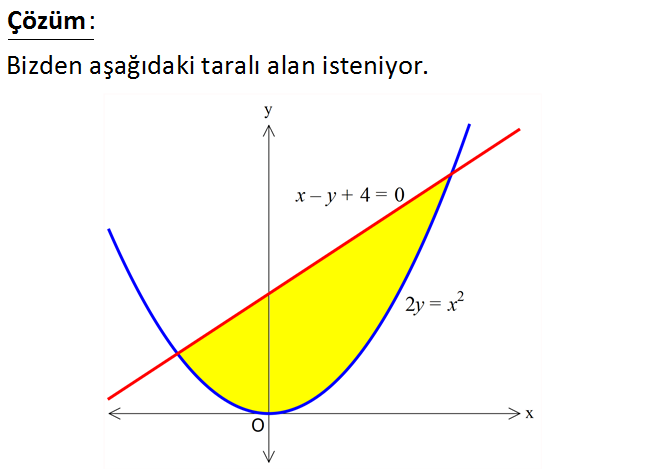
2 2 2y x parabol ile x y 4 0 doğrusu ü ı ı ığ nun s n rlad ı bölgenin alanı kaç br dir? www.matematikkolay.net 2 2 2 2 x 4 x 2 Kesişim noktalarını bulalım. 2y x x x y 4 0 x 4 0 2x x 8 0 2 x 2x 8 0 ( x 4)(x 2) 0 2 4 2 2 3 4 2 2 x 4 ve x 2 dir. Buna göre; taralı alan x 2 ile 4 noktaları arasında; y x 4′ ten x y ‘ye uzanan alandır. 2 x x x x 4 dx 4x 2 2 6 32 4 32 4 8 16 2 8 24 6 3 3 3 3 24 32 4 36 6 30 30 12 18 buluruz. 3 3 3 14
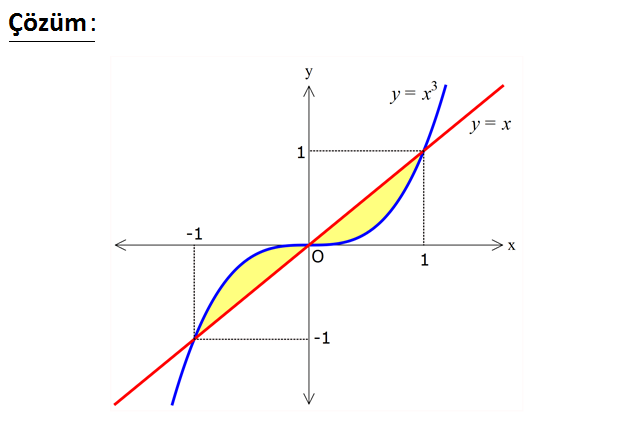
3 2 y x eğrisi ile y x doğrusu arasındaki bölgenin alanı kaç br dir? www.matematikkolay.net 3 3 3 2 y x ile y x’in kesişim noktalarını bulalım. x x x x 0 x(x 1) 0 x(x 1)(x 1) 0 kök 3 1 3 0 1 1 2 4 3 0 0 ler 1,0 ve 1 dir. x ile x arasındaki alan aşağıdaki şekildeki gibidir. (x x )dx integralini hesaplayıp, 2 ile çarpmamız yeterli olacaktır. (2 eş alan olduğu için) x x (x x )dx 2 4 1 1 1 tür. 2 4 4 1 1 2 katını alınca 2 buluruz. 4 2 16
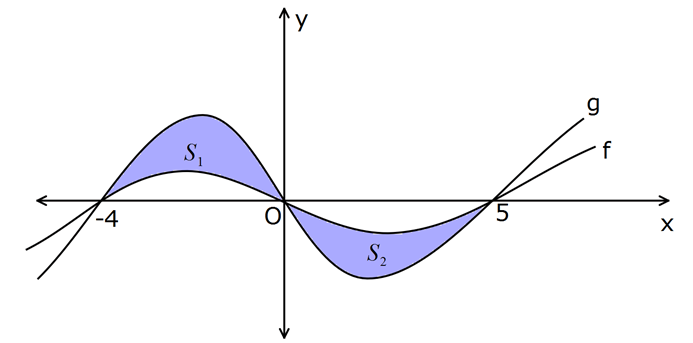
www.matematikkolay.net 1 2 2 1 2 Şekilde S ve S bulundukları kapalı bölg enin alanlarını göstermektedir. S S 24 br ve f(x)g(x) 5 4 2 2 dx 10 olduğuna göre, S kaç br dir? A) 17 B)15 C) 14 D) 13 E) 12 www.matematikkolay.net 5 5 1 2 4 4 1 2 1 2 1 2 2 2 f(x) g(x) dx g(x) f(x) dx S S 10 S S 10 S S 10 S S 24 2 : S 34 S 17 Çözüm 5 4 5 1 2 4 5 5 2 1 4 4 buluruz. NOT : f(x)dx A B dir. g(x)dx S A B S dir. f(x)dx g(x)dx S S olur. 28
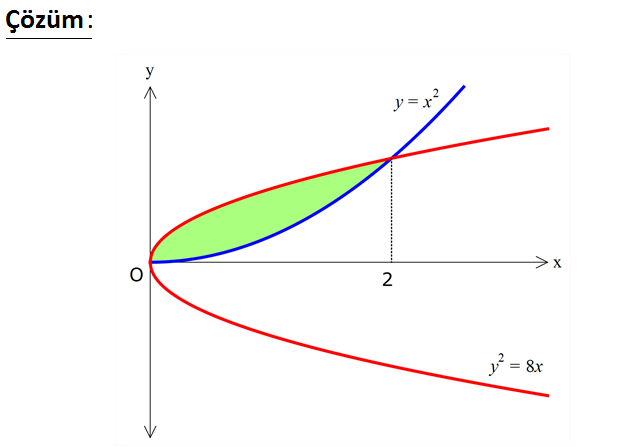
www.matematikkolay.net 2 2 2 Denklemleri y x ve y 8x olan eğrilerin sınırla – dığı bölg enin alanı kaç br dir? 8 16 A) B) C) 2 D 3 3 ) 3 E) 4 www.matematikkolay.net 2 Kesişen yerlerin apsislerini bulalım. y x denkleminin karesini alıp, diğer denkleme eşitleyelim. y 2 4 2 4 4 3 2 x ve y 8x x 8x x 8x 0 x x 8 0 x 0 ve x 2 dir. 0’dan 2’ye kadar integral alacağız. y 8x denklemini y 8x olarak ifade edebil 2 2 2 3 2 2 1 2 3 2 2 2 0 0 0 3 2 iriz. x ve y pozitif olacağından 8x eğrisi x eğrisinden daha büyük değerler aldığı için 0 – 2 arasında 8x ile x eğrileri arasında kalan alan; x x 8x x dx 8x x dx 8 3 3 2 2 8 2 8 8 3 3 3 2 8 16 8 8 8 buluruz. 3 3 3 3 45
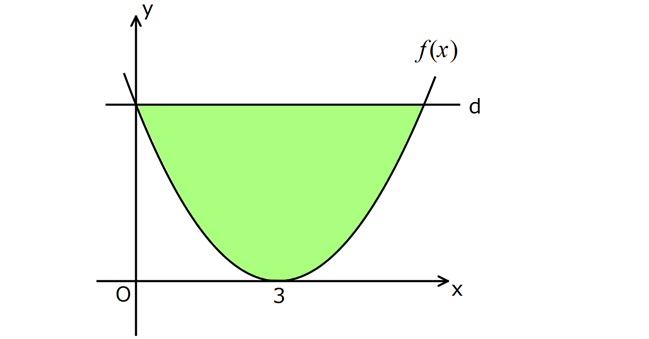
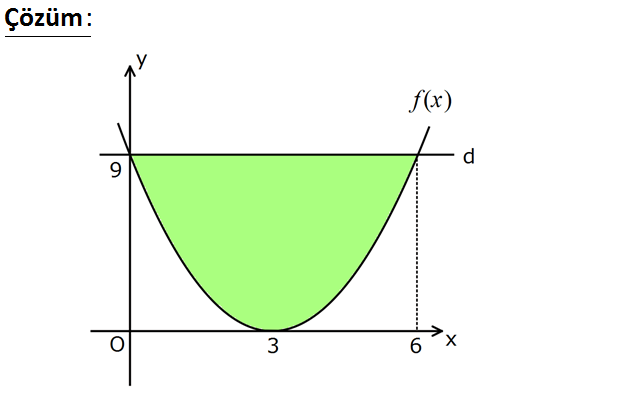
www.matematikkolay.net 2 2 f(x) (x 3) eğrisi ile d doğrusu arasında kalan bölgenin alanı kaç br dir? A) 12 B) 18 C) 27 D) 36 E) 45 : Çözüm www.matematikkolay.net 2 2 2 x 3 eğrisi y eksenini nerde kesiyor, bulalım. x 0 için x 3 0 3 9 dur. Buna göre d doğrusu y 2 6 2 2 0 9 doğrusudur. Eğri ile doğrunun diğer kesiştiği noktayı bulalım. x 3 9 x 3 3 x 6 noktasıdır. Şimdi doğrudan , eğriyi çıkararak integral aldığımızda aradaki alanı bulabiliriz. 9 x 3 dx 9 x 6 0 6 3 6 2 2 0 0 3 2 6x 9 dx x 6x x dx 3x 3 6 3.6 108 72 36 buluruz. 3 48
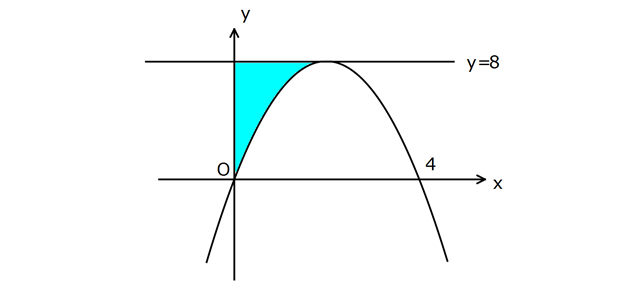
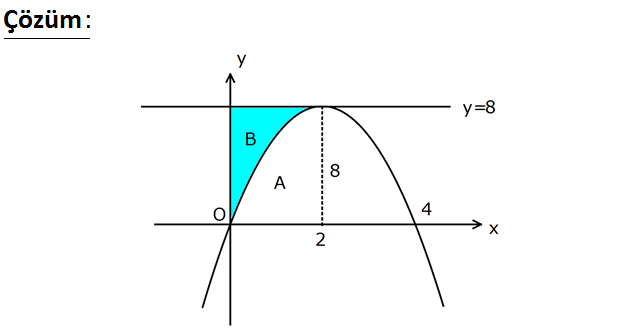
www.matematikkolay.net Şekildeki x eksenini orjinde ve (4, 0) noktasında ke – sen parabolün tepe noktası y 8 doğrusu üzerin 2 de – dir. y ekseni, parabol ve y 8 doğrusunun sınırladığı taralı bölg enin alanı kaç br dir? 4 8 16 22 32 A) B) C) D) E) 3 3 3 3 3 www.matematikkolay.net 2 2 Tepe noktası 2,8 dir. y a x 2 8 0,0 dan geçiyor 0 a 0 2 8 2 2 2 2 2 3 2 2 0 0 a 2 dir. y 2 x 2 8 2 x 4x 4 8 2x 8x 8 8 2x 8x parabolün denklemi Taralı Alan y 8 doğrusu ile parabol arasında kalan alan. A B 2.8 16 dır. 2x A 2x 8x 4x 3 2 16 32 16 3 3 32 16 B 16 A 16 buluruz. 3 3 54
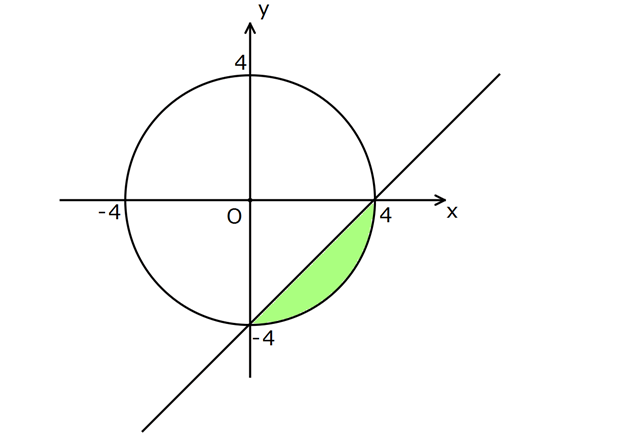
www.matematikkolay.net Yukarıdaki şekilde verilen taralı bölgenin alanı aşağıdaki hangi integral yardımıyla bulunabilir? 4 4 2 2 0 0 4 4 2 2 0 0 4 2 0 A) 16 x x 4 dx B) 16 x x 4 dx C) x 4 16 x dx D) x 4 16 x dx E) x 4 16 x dx www.matematikkolay.net Taralı alanı kapsayan üst çizgiden, alt çizginin çıkarılması gerekir. Sonra integral alı : nır. Ü Çözüm 1 2 2 2 stte bulunan bir doğrudur. Bunun denklemini bulalım. x y x y 1 1 x y 4 4 4 4 y x 4 tür. Çemberin denklemi x y 4 şeklindedir. Tara 2 2 2 2 2 2 4 4 2 2 0 0 lı bölg ede x pozitif, y negatiftir. Buna göre, y’ yi ifade edelim. x y 4 y 16 x y 16 x tir. Şimdi, çıkararak integral alabiliriz. x 4 16 x x 4 16 x 4 2 0 16 x x 4 buluruz. A 38
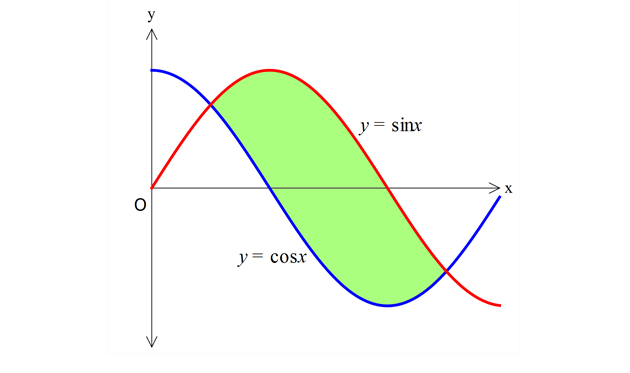
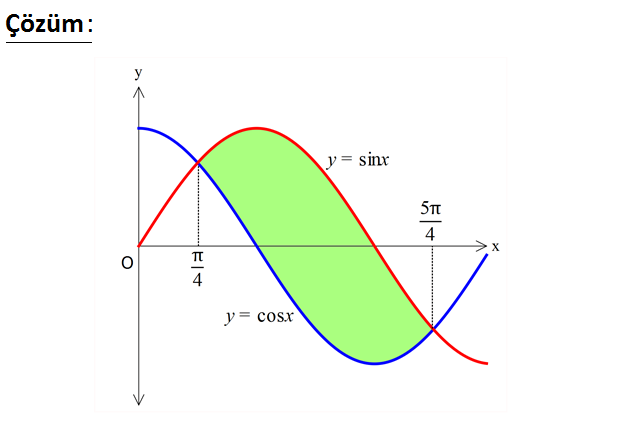
www.matematikkolay.net 2 y cosx ve y sinx eğrileri arasında kalan taralı alan kaç br dir? A) 1 B) 2 C) 2 D) 2 2 E) 3 www.matematikkolay.net Önce sinx ve cosx’ in kesişim noktalarını bulalım; sinx cosx tanx 1 dir. 5 x ve olur. 4 4 4 (si 5 4 5 4 4 4 nx cosx)dx cosx sinx 5 5 cos sin cos sin 4 4 4 4 2 2 2 2 2 2 2 2 2 2 2 2 bulunur. 19
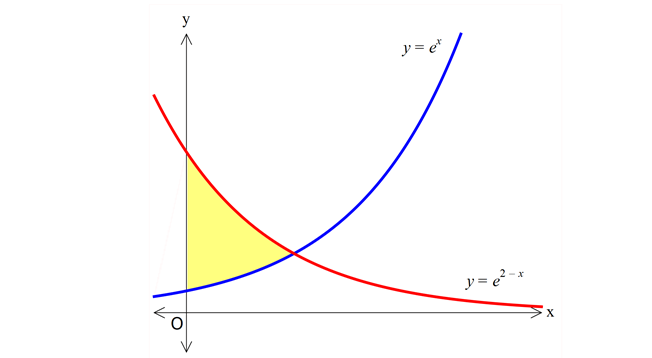
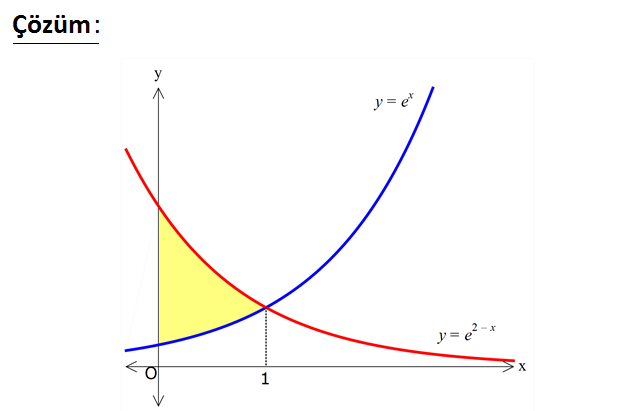
www.matematikkolay.net 2 2 2 2 Yukarıdaki grafikle gösterilen taralı bölgenin alanı kaç br dir? A) (e 1) B) e C) e 1 2 2 D) e 2 E) (e 1) www.matematikkolay.net x 2 x x 2 x y e ile y e eğrilerinin kesiştiği yeri bulalım. e e x 2 x 2x 2 x 1 di 2 x x 1 1 2 x x 0 0 2 x 1 x 1 0 0 1 2 1 0 r. e in altında e in altında Taralı alan kalan alan kalan alan e .dx e .dx e e e e e e 2 2 2 2 e e e 1 e e e 1 e 2e 1 e 1 buluruz. 41
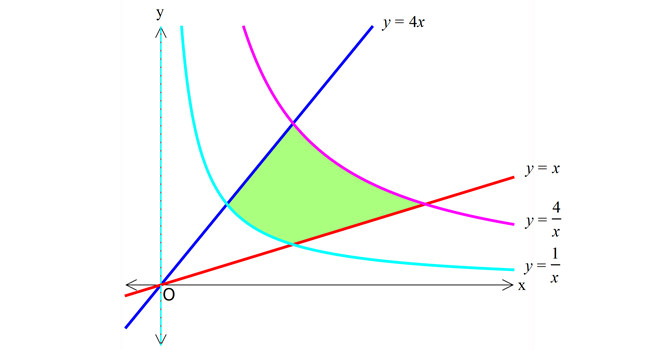
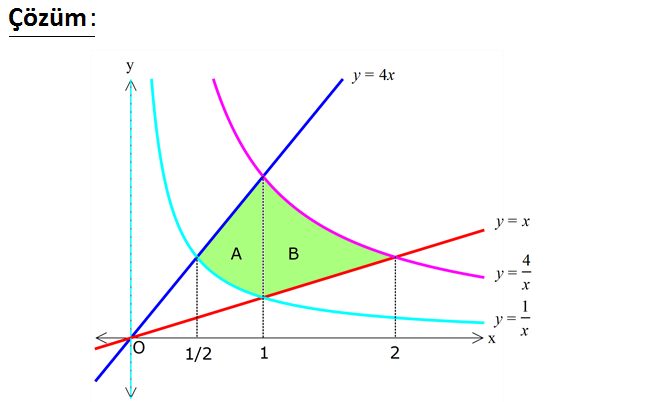
www.matematikkolay.net 2 Yukarıdaki şekilde verilen taralı bölg enin alanı kaç br dir? 3 3 A) 3ln2 B) ln2 C) ln2 2 2 3 3 D) 3ln2 E) 2ln2 2 2 www.matematikkolay.net Kesişen yerlerin apsislerini bulalım. 1 1 4x x x 2 4 4x x 1 x 1 x x 1 x 4 x x 2 x Taralı alan 1 2 2 2 2 1 01.Şub 1 1 1 2 A B 1 4 x 4x x 2x lnx 4lnx x x 2 1 1 1 2 ln1 ln 4ln2 2 4ln1 2 2 2 1 2 2 1 ln2 4ln2 2 2 3ln2 buluruz. 44
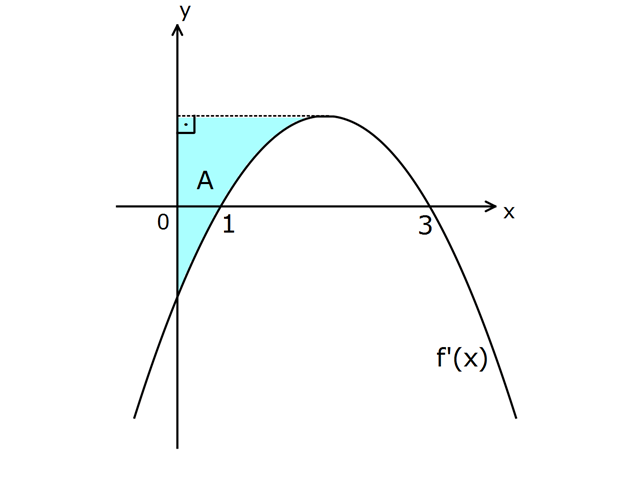
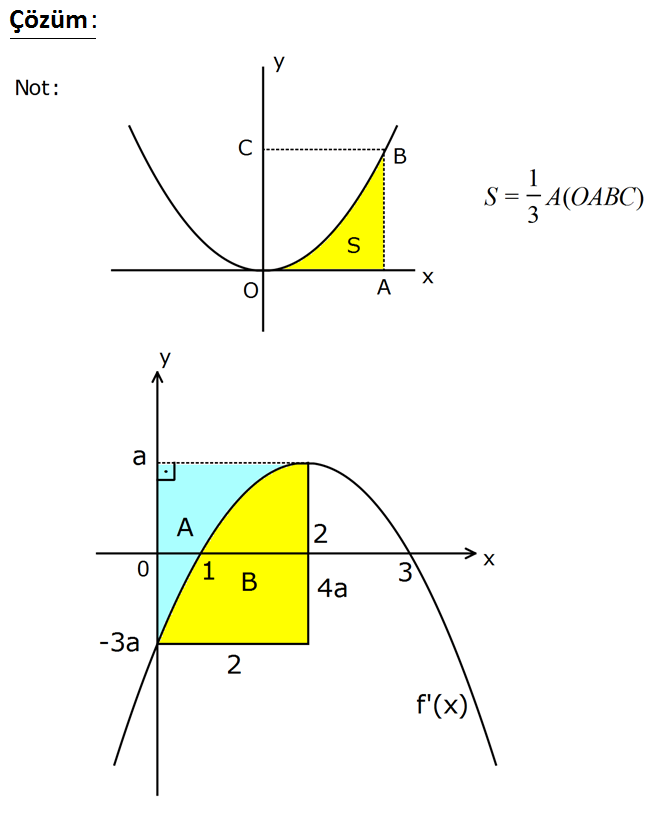
Bir f fonksiyonunun türevi olan f ‘(x) fonksiyonunun grafiği yukarıdaki gibi bir paraboldür. Taralı o 8 larak verilen A bölgesinin alanı birimkare 3 olduğuna göre, f(2) f(0) farkı kaçtır? 2 3 3 10 16 A) B) C) D) E) 3 2 2 3 3 www.matematikkolay.net www.matematikkolay.net 2 8 Buna göre A B 3 8 dir. 3 Grafikteki parabolun denklemini bulalım. r 2 dir. a(x 2) k x 1 içi 2 2 2 n a(1 2) k 0 k a dır. Buna göre parabol denklemi; a(x 2) a şeklindedir. x 0 için 3a dır. A B 4a.2 8a dır. (Dikdörtgenin alanı) A B 8 idi. a 1 buluruz. f ‘(x) (x 2) 1 dir. f( 3 3 3 (x 2) x) x C dir. 3 Buna göre; (2 2) (0 2) f(2) f(0) 2 0 3 3 8 2 2 buluruz. 3 3 13

