Soru Sor sayfası kullanılarak Fonksiyonlar konusu altında Ters Fonksiyon Soruları ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
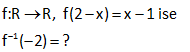

2.SORU
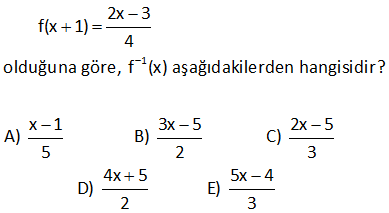

3.SORU

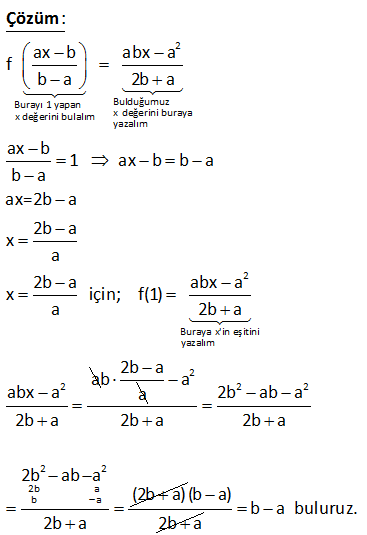
4.SORU


5.SORU


6.SORU

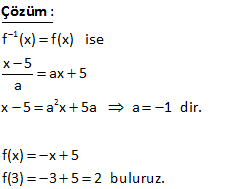
7.SORU


8.SORU
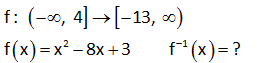

9.SORU
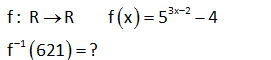

10.SORU
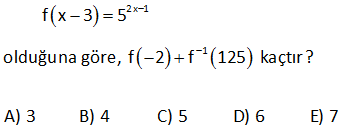

Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
1 f:R R, f(2 x) x 1 ise f ( 2) ? 1 1 f fonksiyonu, f fonksiyonun tersidir. Soruda bizden f ( 2) nin kaça eşit olduğu isteniyor. Bu, f fonsiyonu, hangi değer için 2 değerini alır demekle aynı şeydir. Bunun için; f(2 x) x 1 fo ks y : n i Çözüm 1 onu hangi x için, 2 değerini verir, onu bulalım. x 1 2 x 1 buluruz. Bu değeri f(2 x) x 1 fonksiyonundaki içerideki ifadedeki x’in yerine yazalım, 2 x 2 ( 1) 3 buluruz. Cevap: f ( 2) 3 2 1 2x 3 f(x 1) 4 olduğuna göre, f (x) aşağıdakilerden hangisidir? x 1 3x 5 2x 5 A) B) C) 5 2 3 4x 5 5x 4 D) E) 2 3 www.matematikkolay.net 1 Bulduğumuz Bu ifadenin ters ifadeyi tersini alalım x yerine yazalım 1 2x 3 2x 3 f(x 1) f ( ) x 1 4 4 2x 3 4x 3 tersi 4 2 Bu değeri de x gördüğümüz yere yazalım. 4x 3 4x 5 f (x) 1 buluruz. 2 2 DOĞRU : Cevap Çözüm : D şıkkı 8 2 Tanımlı olduğu bir f fonksiyonu için ax b abx a f b a 2b a eşitliği veriliyor. Buna göre, f(1) aşağıdakilerden hangisine eşittir? A) 2b a B)b a C) b a D) 2a b E) a 3b 2 Burayı 1 yapan Bulduğumuz x değerini bulalım x değerini buraya yazalım 2 Buraya x’in eşitini yaza ax b abx a f b a 2b a ax b 1 ax b b a b a ax=2b a 2b a x a 2b a abx a x için; f(1) a b a : 2 Çözüm lım 2:00 AM abx a 2b a 2b a b a 2 2 2 2 2 2b a b a a 2b ab a 2b a 2b a 2b ab a (2b a) 2b a (b a) 2b a b a buluruz. www.matematikkolay.net 31 2 1 f : A B fonksiyonu birebir ve örtendir. x.f (x) 3f(x) x 7 olduğuna göre, f 3 kaçtır? A) 1 B) 2 C) 3 D) 4 E) 6 1 2 2 2 f (3) a olsun f(a)=3 diyebiliriz. Buna göre soruda verilen denklemde x yerine a yazarsak x.f (x) 3f(x) x 7 a.f (a) 3f(a) a 7 a.3 3.3 a 7 a.9 9 : a 7 9a 9 a 7 8a 16 a 2 buluruz. Çözüm 32 1 f x fonksiyonu tanımlı olduğu aralıkta birebir ve örtendir. 2f x x.f x 3 x olduğuna göre, f x fonksiyonu aşağıdakilerden hangisidir? 2x 3 2x 3 3 x A) B) C) x 1 x 1 1 x x 3 2x 1 D) E) x 2 x 2 1 1 f (x) fonksiyonunu bulmak için ifadede x’i çekmek yeterli olacaktır. 2f(x) x.f(x) 3 x 2f(x) 3 x.f(x) x 2f(x) 3 x. f(x) 1 2f(x) 3 2x 3 x f (x) buluruz. f(x) 1 x 1 : Çözüm www.matematikkolay.net 53 1 a R olmak üzere f x ax 5 fonksiyonu için f x f x ise f 3 kaçtır ? A) 2 B) 3 C) 4 D) 5 E) 6 1 2 f (x) f(x) ise x 5 ax 5 a x 5 a x 5a a 1 dir. f(x) x 5 f(3) 3 5 2 buluruz. : Çözüm 74 sA 3 olmak üzere, A dan A ya tanımlı fonksiyonlardan kaç tanesinin tersi yoktur? m 3 S(A) m ve S(B) n olsun. A’dan B’ye fonksiyon sayısı n dir. A’dan A’ya birebir örten fonksiyon sayısı m! dir. Buna göre, sorunun cevabı; 3 3! 27 6 21 buluruz. : Çözüm 122 2 1 f : , 4 13, f x x 8x 3 f x ? www.matematikkolay.net 2 2 2 2 f x x 8x 3 Her iki tarafa 13 ekleyelim. f x 13 x 8x 3 13 eşitliğin sağ tarafını f x 13 x 8x 16 tam kareye çevirdik. f x 13 x 4 x’i yalnız bırakmak için her iki tarafın karekökünü alalım. f x 13 x : Çözüm 2 1 4 f x 13 x 4 tür. x’in tanım kümesi ,4 olduğundan mutlak değerden işaret değiştirerek çıkar. f x 13 x 4 x 4 f x 13 f x 4 x 13 bulunur. 155 www.matematikkolay.net 3x 2 1 f : R R f x 5 4 f 621 ? 3x 2 1 3x 2 1 3x 2 621 3x 2 3x 2 3x 2 4 f x 5 4 f 5 4 x tir. f 5 4 x 5 4 621 5 625 5 5 3x 2 4 3x 6 x 2 bulunur. : Çözüm 159 2x 1 1 f x 3 5 olduğuna göre, f 2 f 125 kaçtır? A) 3 B) 4 C) 5 D) 6 E) 7 www.matematikkolay.net 2x 1 2.1 1 1 2x 1 1 2x 1 1 2x 1 2x 1 3 f x 3 5 f 2 için içeriyi 2’ye eşitleyelim. x 3 2 x 1 bulunur. f 2 5 5 5 dir. f x 3 5 f 5 x 3 tür. f 125 için 5 125 5 5 2x 1 : 3 Çözüm 1 1 2x 4 x 2 dir. f 125 2 3 1 dir. f 2 f 125 5 1 4 bulunur. 165


4, SORUDA F İN TERSİ (-3) YAZILMIŞ F (3) DİYE İŞLEME ALINMIŞ RİCA ETSEM BAKABİLİR MİSİNİZ ?
Uyarınız için teşekkürler. f’in tersi 3 sorulacaktı. Yazım hatası yapılmış. Şimdi düzeltildi.
3.soruda foksiyonun eşitliğinin sağ tarafındaki paydada 2b-a yazarken, çözümde 2b+a yazılmış.
Teşekkürler. Soru düzeltildi şimdi.
Çok Teşekkürler
2. Soruda 2x-3/4 nin tersi 4x+3/2 olarak yazılmış fakat 4x-3/2 olması gerekmez mi?.Ve zaten 2x-3/4 ifadesinin yanına f – olarak yani tersi olarak geçmiş. Fakat sorna tekrar aynı ifadedin yqni 2x-3/4ün tersini almışsınız. Zaten ters olan ifadenin niye tekrar tersini aldınız. Yanlış olabilir ama yinede sormak istedim
Çözümde bir yanlışlık göremedik. (2x-3)/4 ün tersi de (4x+3)/2 dir. f-((2x-3)/4) ifadesini f-(x) e dönüştürebilmek için içerisinin tersini buluyoruz. İsterseniz burada x gördüğünüz yere (4x+3)/2 yazın. İçerisinin sadece x kaldığını göreceksiniz.