Soru Sor sayfası kullanılarak Fonksiyonlar konusu altında Tanım Kümesi, Görüntü Kümesi Soruları ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU


3.SORU


4.SORU


5.SORU


6.SORU

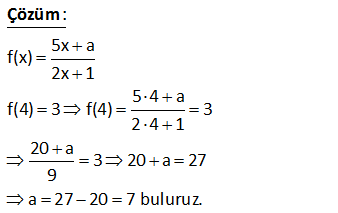
7.SORU
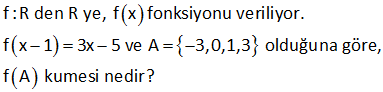

8.SORU


9.SORU


10.SORU
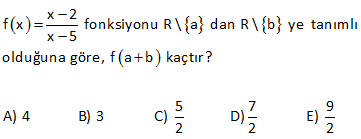

11.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
f : 2, 4 R olmak üzere, 4x 3 f(x) 2 fonksiyonu veriliyor. Buna göre, fonksiyonun görüntü kümesindeki tam sayıların toplamı kaçtır? A) 36 B) 42 C) 48 D) 50 E) 54 Görüntü kümesi, fonksiyonun alabileceği değerleri ifade eder. Tanım kümesinin ( 2,4] olduğu soruda verilmiş. Bu x aralığı için fonksiyonun hangi değerleri alabileceğini bulalım. x 2 için f(x) : Çözüm Toplamları 0 4x 3 8 3 5 2 2 2 4x 3 16 3 19 x 4 için f(x) dir. 2 2 2 Buna göre; Tanım kümesi ( 2,4] ise 5 19 Görüntü Kümesi de ( , ] aralığıdır. 2 2 Bu aralıktaki tam sayı değerleri; 2, 1,0,1,2,3,4,5,6 ,7,8,9 Toplamları 3 4 5 6 7 8 9 42 buluruz. www.matematikkolay.net 17 f : A R f(x) 3 x 1 fonksiyonu veriliyor. Buna göre, A kümesinde tam sayı olan kaç tane eleman vardır? A) 5 B) 6 C) 7 D) 8 E) 9 www.matematikkolay.net f(x) 3 |x 1| 3 |x 1| 0 olmalıdır. |x 1| 3 |x 1| 3 3 x 1 3 4 x 2 x’in alabileceği değerler : 4, 3,….,2 2 ( 4) Terim Sayısı 1 6 1 7 buluruz. 1 : Çözüm 20 f(x) 6 x 5 fonksiyonunun en geniş görüntü kümesi aşağıdaki – lerden hangisidir? A) ( , 6] B) [6, ) C) (5, 6) D) (5, 6] E) [5, 6) f(x) f(x) 6 x 5 Köklü ifade, negatif olamaz. x 5 0 iki tarafı ( ) ile çarpalım. Eşitsizlik yön değiştirir. x 5 0 (iki tarafa 6 ekleyelim) 6 x 5 6 f(x) 6 : buluruz. Görüntü Kümesi: Çözüm ( ,6] dır. Doğru Cevap : A şıkkı 22 1 f : R R olmak üzere, 2ax 7 f(x) (a 1)x 6 fonksiyonu bire bir ve örten olduğuna göre, f (a) değeri kaçtır? 10 9 13 A) 2 B) C) D) E) 7 3 2 2 www.matematikkolay.net 0 olmalı Fonksiyon, birebir ve örten ise tanımsız olduğu bir değer olmamalıdır. Eğer kesrin paydası 0 olursa kesir tanımsız olur. O yüzden paydada x ‘e bağlı bir şey olmamalıdır. Yani; (a 1)x 6 a : Çözüm 1 1 0 a 1 dir. Buna göre; 2ax 7 2x 7 f(x) olur. (a 1)x 6 6 f (1)’i bulalım. 2x 7 1 2x 7 6 2x 13 6 13 x buluruz. 2 38 f : R R tanımlı bir fonksiyon (m 1)x 1 f(x) (m 2)x m olduğuna göre, f(n) 8 eşitliğini sağlayan n değeri kaçtır? A) 5 B) 4 C) 3 D) 2 E) 1 www.matematikkolay.net 0 (m 1)x 1 f(x) fonksiyonun tanımlı (m 2)x m olabilmesi için payda hiç bir zaman 0 olmamalıdır. Bu sebeple paydada x’e bağlı bir ifade olmamalı yani x’in katsayısı 0 olmalıdır. m 2 0 m 2 dir : Çözüm . 3x 1 f(x) Şimdi n’ yi bulalım 2 3.n 1 f(n) 8 2 3n 1 16 3n 15 n 5 buluruz. 41 1 5 f : R R de tanımlı, 2 2 5x a f(x) 2x 1 fonksiyonu bire bir ve örtendir. f 4 3 olduğuna göre, a değeri kaçtır? A) 4 B) 7 C) 8 D) 10 E) 11 www.matematikkolay.net 5x a f(x) 2x 1 5 4 a f(4) 3 f(4) 3 2 4 1 20 a 3 20 a 27 9 a 27 20 7 buluru : z. Çözüm 46 f :R den R ye, f x fonksiyonu veriliyor. f x 1 3x 5 ve A 3,0,1,3 olduğuna göre, f A kumesi nedir? a a : f(x) fonksiyonunu bulalım; f(x 1) 3x 5 f(x 1) 3x 3 2 f(x 1) 3(x 1) 2 f(x) 3x 2 olur. Şimdi f(A) kümesini bulalım. f( 3) 3( 3) 2 11 f(0) 3.0 2 2 f(1) 3.1 2 1 f(3) 3.3 2 7 f(A) { 11, 2, 1, 7} bul Çözüm uruz. www.matematikkolay.net 64 x f x 4x 8 fonksiyonunun en geniş tanım kümesi aşağıdakilerden hangisidir? A) – ,2 B) 2, C) R D) R- 2 E) R- 0 x f(x) 4x 8 Köklü ifadenin içi negatif olamaz. Ayrıca kesrin pay – dası 0 olamaz. Bu nedenle paydadaki ifade 4x 8 0 olmalıdır. 4x 8 0 4x 8 x 2 olmalıdır. Tanım Kümesi : : (2, ) dur. Çözüm www.matematikkolay.net 80 2 2 x 1 f x x 9 x 3x 10 fonksiyonunun tanım kümesi R \ A olduğuna göre, A kümesinin elemanlarından kaç tanesi tam sayıdır ? A) 5 B) 6 C) 7 D) 8 E) 9 2 2 2 2 ( 5) (3) ( 5).(3) x 9 köklü ifadenin içi negatif olamaz. x 9 0 x 9 3 x 3 x 2, 1,0,1,2 olamaz. Ayrıca; payda 0 olamaz. x 3x : 10 0 (x 5)(x 3) 0 x 5 veya x 3 olamaz. Bun Çözüm a göre x’in alamayacağı tam sayı değerleri yani A kümesi: 3, 2, 1,0,1,2,5 7 tane 81 x 2 f x fonksiyonu R \ a dan R \ b ye tanımlı x 5 olduğuna göre, f a b kaçtır ? 5 7 9 A) 4 B) 3 C) D) E) 2 2 2 1 1 : ax b dx b Not : f(x) ise, f (x Paydanın 0 olması, kesri tanımsız yapar. Bu yüzden x 5 olamaz. a 5 tir. Fonksiyonun tersini aldığımızda; 5x 2 f (x) olur. Burda da x 1 olamaz. x 1 Yan ) cx d cx a Çözüm i b 1 dir. Buna göre x 2 6 2 4 f(a b) f(5 1) f(6) 4 buluruz. x 5 6 5 1 84 f : R a R 2 bx 5 f x 2x 1 biçiminde tanımlanıyor. Buna göre, a.b çarpımı kaçtır? A) 2 B) 1 C) 1 D) 3 E) 4 www.matematikkolay.net tanım değer kümesi kümesi f :R {a} R {2} a, fonksiyonun tanım kümesinden çıkarılmış. Demek ki fonskiyonu tanımsız yapıyor. Kesirli bir ifadede paydayı 0′ yapan değer için fonksiyon tanımsızdır. : bx f(x) Çözüm 1 tanım kümesi değer kümesi 5 eğer payda 0 olursa kesir 2x 1 tanımsız olur. 1 2x 1 0 2x 1 x a’dır. 2 Eğer fonksiyonun tersi alınırsa değer kümesi ile tanım kümesi yer değiştirir. 1 f :R {2} R 2 1 1 2, fonksiyonun ter sinin tanım kümesinden çıkarılmış. Demek ki paydayı tanımsız yapıyor. Paydadaki x, 2 olamaz. ax b dx b Not : f(x) f (x) cx d cx a bx 5 1.x 5 f(x) f (x) 2x 1 2x b x 2 paydayı 0 yapıyord u; 2x b 0 2.2 b 0 4 b 0 b 4 tür. 1 Buna göre; a.b 4 2 buluruz. 2 137


9’uncu bir hata vardır
x²_3x_10 = (x_5) (x+2)
Uyarınız için teşekkürler. Hata düzeltildi.
Çok güzel teşekkürler