Soru Sor sayfası kullanılarak Fonksiyonlar konusu altında Sabit fonksiyon, Birim fonksiyon soruları ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
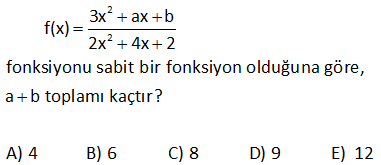

2.SORU


3.SORU


4.SORU
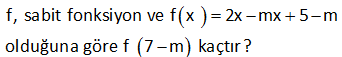

5.SORU
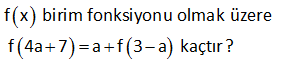
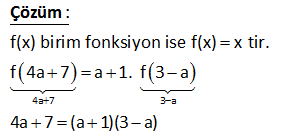
6.SORU


7.SORU
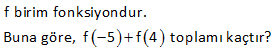

8.SORU


9.SORU
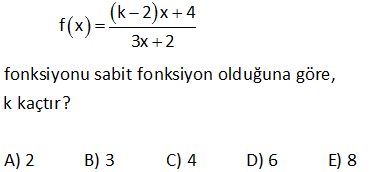

10.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
2 2 3x ax b f(x) 2x 4x 2 fonksiyonu sabit bir fonksiyon olduğuna göre, a b toplamı kaçtır? A) 4 B) 6 C) 8 D) 9 E) 12 2 2 Sabit fonksiyon demek, f(x) fonksiyonunda x’e bağlı bir değişkenin olmayacağı anlamına gelir. Bu da ancak kesrin payı ile paydası arasında sabit bir oran olursa gerçekleşir. 3x ax b f(x) 2x 4x : 2 Çözüm 2 3 x ‘ler arasında oranı var. 2 Diğer terimlerde de aynı oran olmalıdır. a 3 2a 12 a 6 dır. 4 2 b 3 b 3 tür. 2 2 Buna göre; a b 6 3 9 buluruz. www.matematikkolay.net 16 f : R R olmak üzere, f(3x 1) (2a 9)x 3b 4 fonksiyonu birim fonksiyon olduğuna göre, f(a.b) değeri kaçtır? A) 4 B) 2 C) 3 D) 5 E) 6 www.matematikkolay.net 3x 1 3 1 Birim fonksiyonun içi ile dışı birdir. Yani f(x) x tir. f(3x 1) (2a 9)x 3b 4 3x 1 (2a 9)x 3b 4 2a 9 3 2a 12 a 6 3b 4 1 3b 3 b 1 dir. f(a.b : ) f(6.1) f(6) 6 buluruz. Çözüm 40 f : [ 2,3] R , f(x) 2x 3 olduğuna göre f([ 2,3]) görüntü kümesini bulunuz. Fonksiyonun alabileceği en küçük ve en büyük değeri bulalım. Görüntü kümesi bu değerler arasındaki tüm sayılardır. En küçük değer : F( 2) 2.( 2) 3 : 4 Çözüm 3 7 dir. En büyük değer : F(3) 2.3 3 6 3 3 tür. Buna göre Görü ntü Kümesi: [ 7,3] aralığıdır. www.matematikkolay.net 51 f, sabit fonksiyon ve f x 2x mx 5 m olduğuna göre f 7 m kaçtır? 0 : Sabit fonksiyonda x değişkeninin katsayısı 0 olmalıdır. f(x)=2x mx 5 m 2x mx 0 m 2 dir. Buna göre; f(x)=5 m 5 2 3 tür. f(x) 3 tür. f(7 m) de 3 olacaktır. Çünkü fonksiyon her zaman Çözüm 3 değerini vermektedir. Cevap: 3 56 f x birim fonksiyonu olmak üzere f 4a7 a f 3a kaçtır? 4a 7 3 a : f(x) birim fonksiyon ise f(x) x tir. f 4a 7 a 1. f 3 a 4a 7 (a 1)(3 a) Çözüm 61 www.matematikkolay.net f sabit fonksiyon olmak üzere, 3x 10 f x olduğuna göre, f m kaçtır ? mx 5 5 3 A) 4 B) 3 C) D) 2 E) 2 2 ax b a b Not : f(x)= Sabit fonksiyon ise dir. cx d c d 3 10 3.5 3 Buna göre tir. m= dir. m 5 10 2 3x 10 Buna göre f(x)= 2 dir. Yani f(x) daima 2 3 x 5 2 değerine eşittir. Dolayısıyla f : (m) de 2 olacak Çözüm tır. 62 f birim fonksiyondur. Buna göre, f 5 f 4 toplamı kaçtır? Birim fonksiyonda; Fonksiyonun içindeki ifade aynı şekilde dışarı çıkar. Buna göre; f( 5) f(4) 5 4 1 buluruz. : Çözüm 110 f birim fonksiyondur. a 2 a 1 f olduğuna göre, a kaçtır? 3 2 www.matematikkolay.net a 2 a 1 içler dışlar çarpımı yapalım 3 2 2a 4 3a 3 2a 3a 3 4 a 7 a 7 buluru . : z Çözüm 111 k 2x 4 f x 3x 2 fonksiyonu sabit fonksiyon olduğuna göre, k kaçtır? A) 2 B) 3 C) 4 D) 6 E) 8 k 2x 4 f x fonksiyon sabit fonksiyon ise; 3x 2 k 2 4 k 2 2 3 2 3 k 2 6 k 8 bulunur. : Çözüm www.matematikkolay.net 174 f x 5x a.b x b 4 fonksiyonu birim fonksiyon olduğuna göre, a.f 2 değeri kaçtır? A) 4 B) 2 C) 1 D) 1 E) 2 birim fonksiyon olması için tamamının x’e eşit olması gerekir. 0 x f x 5x a.b x b 4 5x a.b x b 4 b 4 0 b 4 tür. 5x a.bx x 5 a.b 1 5 a.4 1 a 1 dir. a.f 2 1.2 2 bulu ur. : n Çözüm www.matematikkolay.net 182 www.matematikkolay.net 4x m f x x 3 fonksiyonu bir sabit fonksiyon olduğuna göre, m f m işleminin sonucu kaçtır? A) 4 B) 8 C) 12 D) 16 E) 20 f x sabit fonksiyon ise x’ler arasındaki oran, sabit sayılar arasındaki orana eşit olmalıdır. 4x m m 12 dir. x 3 m 12 olunca; 4.12 12 36 f 12 4 tür. 12 3 9 m f m 12 4 16 bulur z. : u Çözüm 358


Çok güzel olmuş ellerinize sağlık ☺️😊😊
Afiyet olsun
alah razı olsun adamsın
Güzel sorulardı birdaha olmasın
sorular ne kolay ne zor tam orta ayarda ellerinize sağlık