Grafikte ötelemeler, simetri

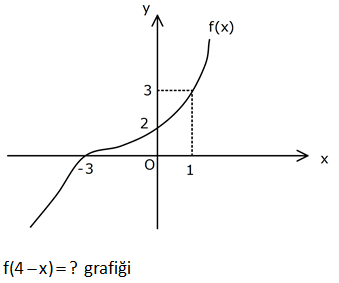
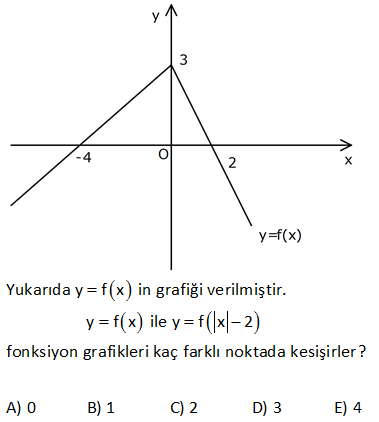
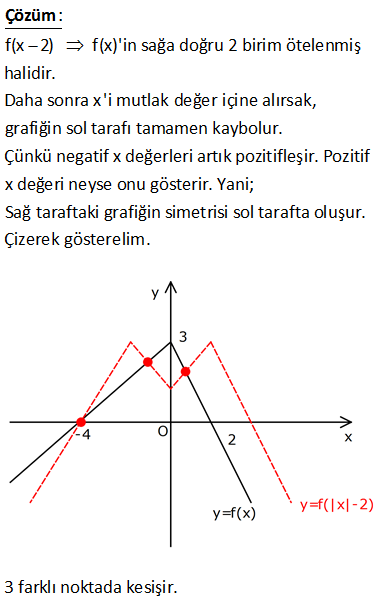
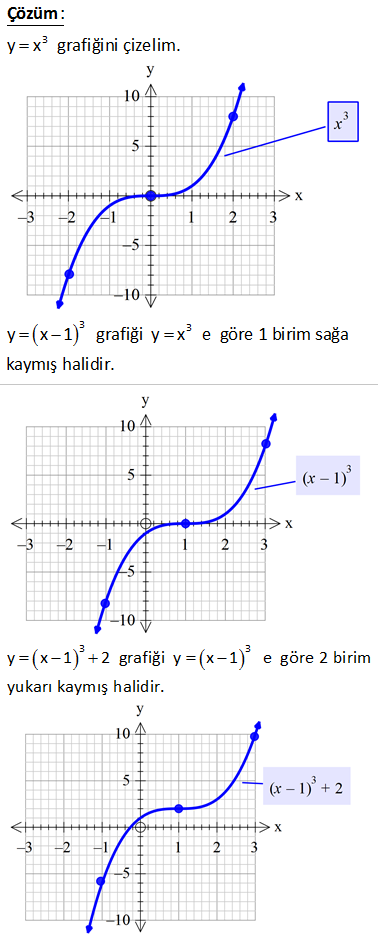
Aşağıda y=f x 2 fonksiyonunun grafiği verilmiştir. Buna göre, y  f x fonksiyonunun grafiğini çiziniz. www.matematikkolay.net f(x) fonkisyonundan f(x 2) elde edilirken fonksiyon x ekseninde 2 birim sola doğru kaydırılır. Şimdi ise, bu işlemin tam tersini yapmalıyız. Yani sağa 2 birim kaydıracağız : .  Çözüm 82 3T 1 3T 1 N(T) 4 e a fonksiyonunu önce 2 birim sağa, sonra x eksenine göre yansıtıp 1 birim yukarı kaydır – dığımızda elde edilen fonksiyonun kuralını bulunuz. b) bu N(T) 4 e fonksiyon ) un       un ters fonksiyonunu bulunuz. www.matematikkolay.net 3T 1 3(T 2) 1 3(T 2) 1 : N(T) 4 e İki birim sağa kayması demek, T yerine T 2 yazmaktır. 4 e olur. x eksenine gör yansıtmak, tüm denklemi 1 ile çarpmaktır. 4 e olur. 1 birim yukarı kaydırmak, den a)              Çözüm       3(T 2) 1 3T 5 3T 1 3T 1 1 kleme 1 eklemektir. 4 e 1 3 e b) y 4 e e 4 y 3T 1 ln 4 y 3T l olur. Düzenle n(4 y rsek; N(T) bulur ) 1 ln 4 y 1 T tür. O halde; 3 ln 4 T 1 N (T) bul u uruz. 3 z.                             247 f(4 x) ? grafiği www.matematikkolay.net f(4 x) f( x 4) f( x) grafiği f(x)’in y eksenine göre simetrisidir. f(x 4) grafiği f(x) in 4 birim sola kaymasına neden olurken f( x 4) grafiği de f( x)’in 4 birim sağa kaymasına neden olur. B : öyl          Çözüm e durumlarda içeriyi 0’a eşitleyerek kaymanın nereye olacağını görebiliriz. x 4 0 x 4 4 birim kayacak. Yani sola x 4 0 x 4 4 birim sağa kayacaktır. f( x 4) grafiği için de f( x)’i 4 biri                 m sağa kaydıracağız. www.matematikkolay.net 263 www.matematikkolay.net       Yukarıda y f x in grafiği verilmiştir. y f x ile y f x 2 fonksiyon grafikleri kaç farklı noktada kesişirler? A) 0 B) 1 C) 2 D) 3 E) 4     f(x 2) f(x)’in sağa doğru 2 birim ötelenmiş halidir. Daha sonra x’i mutlak değer içine alırsak, grafiğin sol tarafı tamamen kaybolur. Çünkü negatif x değerleri artık pozitifleşir. Pozitif x değe :   Çözüm ri neyse onu gösterir. Yani; Sağ taraftaki grafiğin simetrisi sol tarafta oluşur. Çizerek gösterelim. 3 farklı noktada kesişir. 293 www.matematikkolay.net 3 x 2 2 y 3 12 bağıntısı ile sınırlanan kapalı bölg enin alanı kaç birimkaredir? A) 48 B) 54 C) 60 D) 72 E) 108     www.matematikkolay.net x 2 için 0 İkisi de mutlak değer içinde olduğu için, baklava dilimi şeklinde bir grafik ortaya çıkacaktır. Ekseni kesen noktaları bulalım. 3 x 2 2 y 3 12 x 2 olduğunda 2 y 3 12 y 3 6 :            Çözüm y 3 için 0 y 3 veya y 9 dur. 3 x 2 2 y 3 12 y 3 olduğunda 3 x 2 12 x 2 4 x 6 veya x 2 dir. Buna göre çiz                    elim. 2 Köşegenler çarpımı 8.12 Alan 48 br dir. 2 2    294  3 y x  1 2 nin grafiği ? 3 : y  x grafiğini çizelim. Çözüm  3 3 y x 1 grafiği y x e göre 1 birim sağa kaymış halidir.    www.matematikkolay.net     3 3 y x 1 2 grafiği y x 1 e göre 2 birim yukarı kaymış halidir.      328