Soru Sor sayfası kullanılarak Fonksiyonlar konusu altında Grafik çizme soruları, grafikte alan bulma soruları ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU

2.SORU


3.SORU


4.SORU
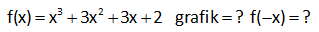
5.SORU


6.SORU

Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
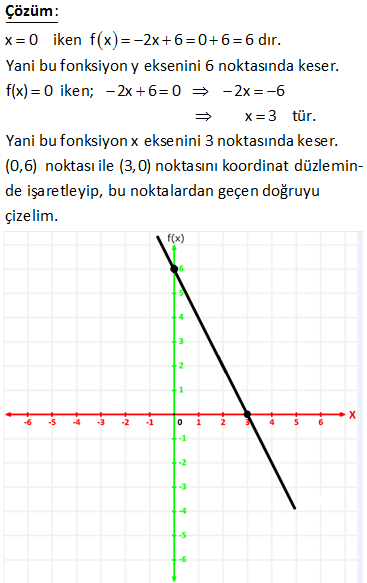
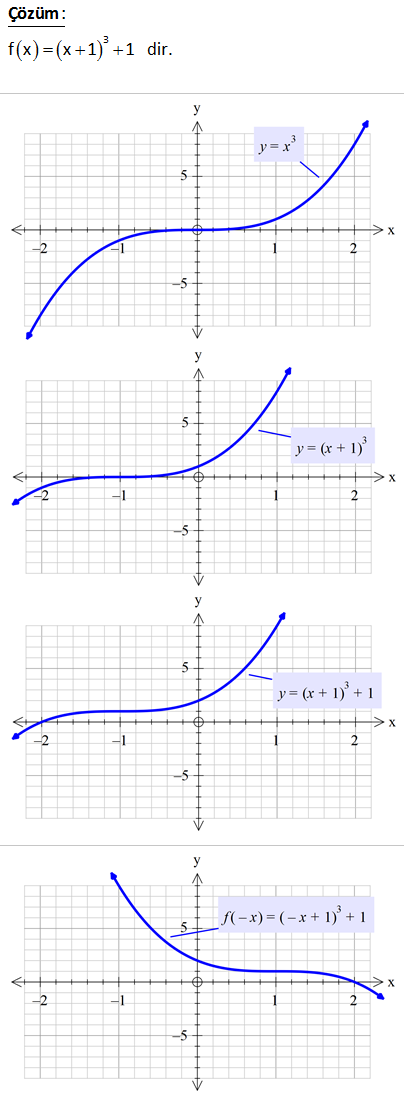
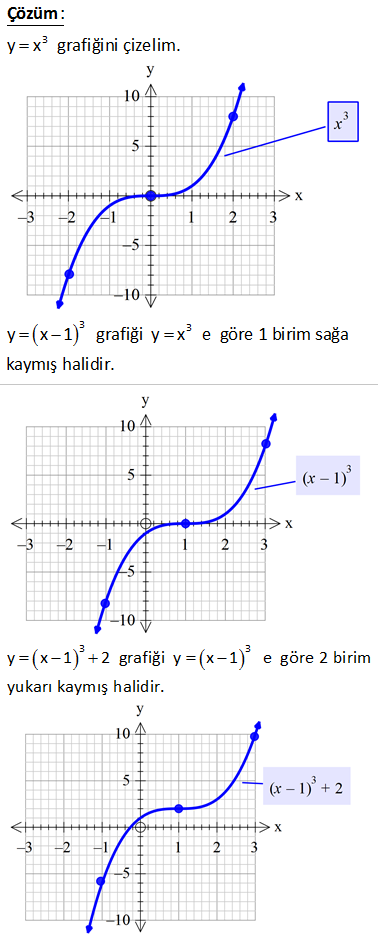
f x 2x 6 fonksiyonun grafiği çiziniz. : f x 2x 6 0 6 6 dır. Yani bu fonksiyon y eksenini 6 noktasında keser. f(x) 0 iken; 2x 6 0 2x 6 x 3 tür. Yani bu fon x 0 iken Çözüm ksiyon x eksenini 3 noktasında keser. (0,6) noktası ile (3,0) noktasını koordinat düzleminde işaretleyip, bu noktalardan geçen doğruyu çizelim. www.matematikkolay.net 3 2 f x x 4 g x 6 x doğruları ve x ekseni arasında kalan kapalı bölg enin alanı kaç br dir ? A) 24 B) 25 C) 28 D) 30 E) 32 f(x) x 4 0 x 4 (x eksenini kesen yer) f(x) 6 x 0 x 6 (x eksenini kesen yer) Birbiriyle kesiştikleri yer : x 4 6 x 2x 2 x 1 dir. x 1 noktasında fonksiyonlar : 5 değ Çözüm erini alır. www.matematikkolay.net 2 Buna göre bizden istenen alan bir üçgendir. Bu üçgenin tabanı 10, yüksekliği ise 5 birimdir. 10.5 50 Alan 25 br buluruz. 2 2 102 f : R R olmak üzere, f x 4 x 2 fonksiyonunun koordinat eksenleri ile oluşturduğu bölgenin alanı kaç birimkaredir ? A) 14 B) 15 C) 16 D) 17 E) 18 Eksenleri kesen noktaları bulalım. x 0 için f(x) 4 |0 2| 4 2 2 dir. y 0 için 0 4 |x 2| x 2 veya 6 dır. dır. f(x) en büyük değeri de, mutlak değerin içini 0 yapan x 2 noktasında alır. f(2 : ) Çözüm 4 tür. Buna göre f(x)’i çizersek; www.matematikkolay.net Büyük üçgenden, küçük üçgenin alanını çıkararak, taralı alanı bulabiliriz. 8.4 2.2 16 2 14 buluruz. 2 2 116 3 2 f(x) x 3x 3x 2 grafik ? f(x)? 3 : f x x 1 1 dir. Çözüm www.matematikkolay.net www.matematikkolay.net 261 www.matematikkolay.net f : R R , f : “x ten sıfıra kadar taralı bölgenin alanı” şeklinde f fonksiyonu tanımlanıyor. Buna göre, f 8 in değeri kaçtır? A) 44 B) 46 C) 48 D) 50 E) 52 www.matematikkolay.net Eksenleri 2 ve 2 noktasında kesen doğrunun denklemi x y 1 şeklindedir. 2 2 x 8 olursa, 8 y y 1 4 1 y 10 dur. : 2 2 2 Çözüm Buna göre, taralı alan; 10 2 12 Yamuğun alanı 8 8 48 buluruz. 2 2 Cevap: C 308 3 y x 1 2 nin grafiği ? 3 : y x grafiğini çizelim. Çözüm 3 3 y x 1 grafiği y x e göre 1 birim sağa kaymış halidir. www.matematikkolay.net 3 3 y x 1 2 grafiği y x 1 e göre 2 birim yukarı kaymış halidir. 328

