Soru Sor sayfası kullanılarak Fonksiyonlar konusu altında f(x) cinsinden yazma ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
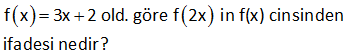

2.SORU
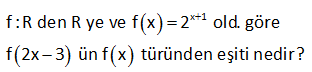

3.SORU
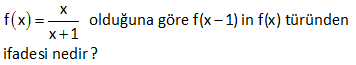

4.SORU

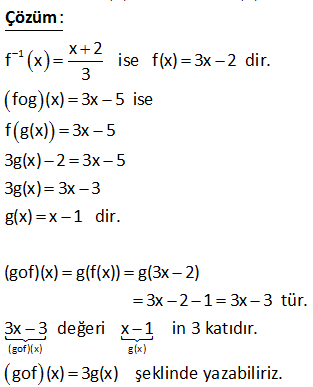
5.SORU
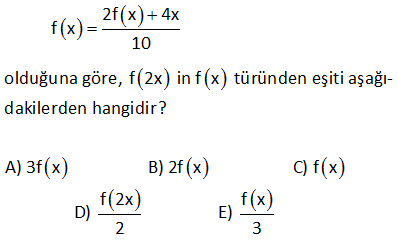
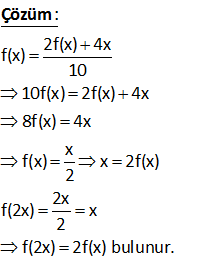
6.SORU


7.SORU

8.SORU


9.SORU

Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
f x 3x 2 old. göre f 2x in f(x) cinsinden ifadesi nedir? : f(2x) fonksiyonu için f(x) fonksiyonunda x gördüğümüz yere 2x yazalım. f(2x) 3(2x) 2 6x 2 dir. Bulduğumuz fonksiyonu f(x) fonksiyonu cinsinden nasıl yazarız şimdi ona bakalım. f(x) fonksiyonunun 2 k Çözüm atını alalım; 2f(x) 2(3x 2) 6x 4 tür. Bundan da 2 yi çıkarırsak f(2x)’in eşitini bulmuş oluruz. O halde; f(2x) 2f(x) 2 buluruz. www.matematikkolay.net 63 x 1 f :R den R ye ve f x 2 old. göre f 2x 3 ün f x türünden eşiti nedir? x 1 x x 2x x 2 2x 3 1 2x 2 2 x 2 x 2 2 : f(x) f(x) 2 f(x) 2 .2 2 2 2 (2 ) f(2x 3) 2 2 2 4 Şimdi 2 gördüğümüz yere eşitini yazalım; f(x) (2 ) 2 f (x) f(2x 3) buluruz. 4 4 16 Çözüm www.matematikkolay.net 66 x f x olduğuna göre f x 1) in f(x) türünden x 1 ifadesi ne ( dir? www.matematikkolay.net : f(x 1) fonksiyonunu bulalım; x 1 x 1 f(x 1) dir. x 1 1 x f(x) fonksiyonunda x i f(x) cinsinden elde edelim; x f(x) f(x).(x 1) x f(x).x f(x) x x 1 f(x) x f(x).x f(x) x(1 f(x)) f(x) x dir. 1 f(x) Şimdi bu Çözüm değeri f(x 1) fonksiyonunda x yerine yazalım. f(x) f(x) 1 f(x) 1 x 1 1 f(x) 1 f(x) f(x 1) x f(x) 1 f(x) f(x) 1 f(x) 2f(x) 1 buluruz. f(x) 68 www.matematikkolay.net 1 f ve g fonksiyonları birebir ve örtendir. x 2 f x ve f o g x 3x 5 3 olduğuna göre, g o f x in g x türünden değeri aşağıdakilerden hangisidir? A) 2.g x B) 3.g x C) 12.g x 1 D) g x 1 E) 3.g x 1 1 (gof)(x) x 2 f x ise f(x) 3x 2 dir. 3 fog (x) 3x 5 ise f g(x) 3x 5 3g(x) 2 3x 5 3g(x) 3x 3 g(x) x 1 dir. (gof)(x) g(f(x)) g(3x 2) 3x 2 1 3x 3 tür. 3x 3 değeri x 1 : Çözüm g(x) in 3 katıdır. gof (x) 3g(x) şeklinde yazabiliriz. 161 2f x 4x f x 10 olduğuna göre, f 2x in f x türünden eşiti aşağıdakilerden hangidir? A) 3f x B) 2f x C) f x f 2x f x D) E) 2 3 2f(x) 4x f(x) 10 10f(x) 2f(x) 4x 8f(x) 4x x f(x) x 2f(x) 2 2x f(2x) x 2 f(2x) 2f(x) bu : lunur. Çözüm 197 2x 1 f x fonksiyonu veriliyor. x 1 f x 2 fonksiyonunun f x türünden değeri aşağıdakilerden hangisidir? f x 8 f x 7 f x 1 A) B) C) 2f x 7 2f x 8 2 f x f x 2 2f x 6 D) E) f x 1 f x 7 www.matematikkolay.net 2x 1 f x x 1 Bu fonksiyonda x’i çekelim.Yani fonksiyonun ter sini alalım. ax b d.f x b f x x dır. cx d c.f x a 2x 1 f x 1 f x 1 f x x dir. x 1 f x 2 2 f x Şimdi f x 2 fonksiyonunu oluşturalım. 2x 1 2 x 2 f x 2 : f x x 1 Çözüm 1 2x 3 x 2 1 x 3 Şimdi bu fonksiyonda x ‘in eşitini yazalım. f x 1 02.Mar 2 f x 2f x 2 6 3f x f x 2 f x 1 f x 1 6 3f x 3 2 f x f x 8 f x 8 f x 2 bulunur. 2f x 7 2f x 7 206 www.matematikkolay.net x 2 f x x olduğuna göre, f x 2 nin f x türünden değeri aşağıdakilerden hangisidir? 2 f x 2 f x 1 A) B) C) f x 1 f x 2 f x 1 1 f x D) E) 2 f x 2 f x x 2 x 2 x 2 f x ise xf x x 2 x xf x x 2 x f x 1 2 2 x dir. f x 1 x 2 x f x 2 dir. x x 2 x yerine f x cinsinden eşitini yazalım. 2 2 x f x 1 f x 1 x 2 2 2 2f x 2 2 f x 1 f x 1 2 4 2 x : f Çözüm 1 buluruz. 2 f x 341 www.matematikkolay.net x x 3 2 2 3 1 f x 3 3 2 olduğuna göre, f 3x fonksiyonunun f x türünden eşiti aşağıdakilerden hangisidir? A) 2f x B) 4f x C) f x 1 D) 3.f x 4 E) 4.f x 3.f x 3 3 3 x x x x x 3 x 3 3x 2x 3 3 3 3 3 3 3 3 3 Not : a b a b 3ab a b 3 3 a ve b olsun. 2 2 f x a b dir. 3 3 1 Ayrıca a.b . tür. 2 2 4 3 3 3 3 8a 8b f 3x 2 2 2 2 2 2 4a 4b tür. 4a 4b 4 a b 4 a b 3ab a b : Çözüm 3 3 1 4 f x 3 f x 4 4f x 3f x buluruz. 352 www.matematikkolay.net 1 f ve g fonksiyonları birebir ve örtendir. x 2 f x ve f o g x 3x 5 3 olduğuna göre, g o f x in g x türünden değeri aşağıdakilerden hangisidir? A) 2.g x B) 3.g x C) 12.g x 1 D) g x 1 E) 3.g x 1 1 x 2 f x ise f x 3x 2 dir. 3 fog x 3x 5 ise f g x 3x 5 3 g x 2 3x 5 3g x 3x 3 g x x 1 dir. gof x g f x g 3x 2 3x 2 1 3x 3 3 x : 1 Çözüm 3gx buluruz. 354 Tanımlı olduğu yerlerde, x 2 f x x 1 olduğuna göre, f x 1 in f x türünden eşiti aşağıdakilerden hangisidir? 3 f x 2 f x 1 2f x A) B) C) 2 f x 1 f x 1 f x 2f x 1 2f x 1 D) E) 2f x f x www.matematikkolay.net 1 x 1 x 1 x 2 x 2 f x ise f x dir. x 1 x 1 Yani; f x 2 x dir. f x 1 x 2 x 3 f x 1 dir. x 1 x 2 f x 2 x yerine x yazal f x 1 : Çözüm ım. f x 2 f x 2 3f x 3 3 f x 1 f x 1 f x 2 2 f x 1 f x 2 2f x 2 f x 1 2f x 1 tir. f x 361

