Soru Sor sayfası kullanılarak Faktöriyel konusu altında Faktöriyelli İfadelerin Eşitliği ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU


3.SORU


4.SORU
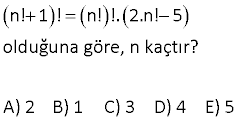
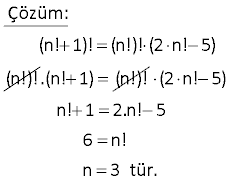
5.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Abone olarak daha fazla sayıda soru sorabilirsiniz. Abone olmak için Tıklayın.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Not: Bu sitede yayınlanan çözümler, tamamen bu site için hazırlanmıştır. İzinsiz olarak yayınlanıp, çoğaltılması yasaktır.
n ve m iki dogal sayıdır. Buna gore n! 6m! esitligini saglayan kac tane n,m dogal sayı ikilisi vardır? Çözüm: 6 yı 2 ve 3’ün çarpımı şekilde n! 6m! 6!=6.5! olabilir. Bu durumda (n,m)=(6,5) n! 3.2.m! 3!=3.2.1! olabilir. Bu durumd yazal a ım. (n,m)=(3,1) 0!=1 olduğundan buradan da bir (n,m) ikilisi çıkar. Bu durumda (n,m)=(3,0) Toplam 3 tane (n,m) ikilisi va rdır. 2 x, y ve z doğal sayılar ve x!.y!.z!=144 olduğuna göre, x y z toplamı en az kaçtır? A) 5 B) 6 C) 7 D) 8 E) 10 www.matematikkolay.net 3! 4! 0! Çözüm: x!.y!.z! 144 0! 1 1! 1 144’ü sadece 6 ile 24’ü çarparak elde 2! 2 edebiliriz. Diğer sayı da 1 olacaktır. 3! 6 Toplamın en az olması için de bunu 4! 24 0! seçelim. 5! 120 6.24.1 144 x y z 3 4 0 7 buluruz. 6 a ve b doğal sayılar olmak üzere a!=24.b! koşulunu sağlayan kaç farklı b değeri vardır? A) 1 B) 2 C) 3 D) 4 E) 5 4.3.2.1 Çözüm: a! 24.b! 24! 24.23! b=23 olabilir. 4! 24 .0! b=0 olabilir. 4! 24.1! b=1 olabilir. Görüldüğü üzere b, 3 farklı değer alabilmektedir. 10 n! 1! n!!.2.n! 5 olduğuna göre, n kaçtır? A) 2 B) 1 C) 3 D) 4 E) 5 www.matematikkolay.net Çö züm: (n! 1)! (n!)! (2 n! 5) (n!)! .(n!1) (n!)! (2 n! 5) n! 1 2.n! 5 6 n! n 3 tür. 14 4! x 1 ! olduğuna göre, x! kaçtır? 4 A) 2 B) 4 C) 12 D) 24 E) 120 Çözüm: 4! (x 1)! 4 4 (x 1)! .3.2.1 4 (x 1)! 3! x 1 3 x 4 tür. Buna göre; x! 4! 4.3.2.1 24 buluruz. 21


Merhaba;
1.soruda 0!=1 olduğu durumda değerler nasıl(3,0) çıkmaktadır?
n=3 ve m=0 olduğunda 3!=6.0! eşitliği oluşur. İki taraf da 6 olduğu için eşitlik sağlanır. Bunu da (3,0) olan (n,m) ikilisi sağlamıştır.