Soru Sor sayfası kullanılarak Dörtgenler konusu altında Dörtgenin İçinde-Dışında Özel Üçgen Oluşturma ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
2.SORU
3.SORU
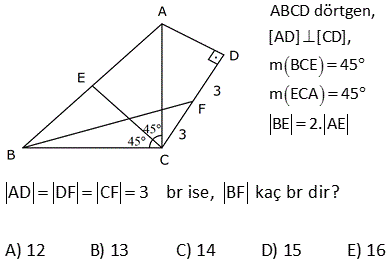

4.SORU
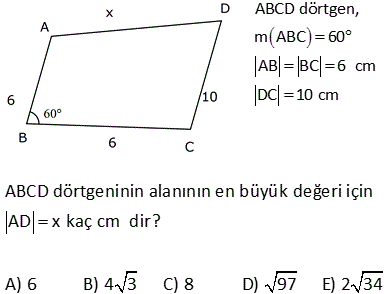
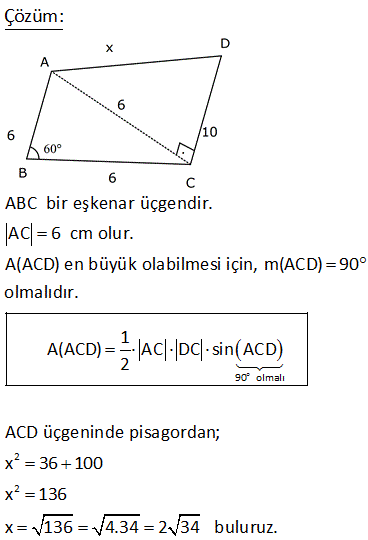
5.SORU
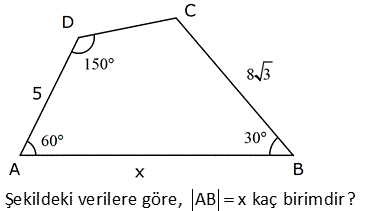

6.SORU
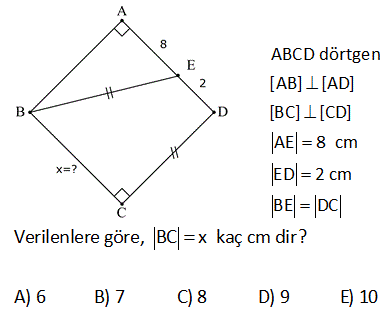
7.SORU
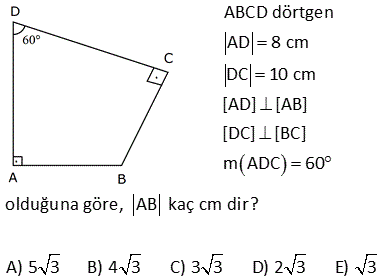

8.SORU
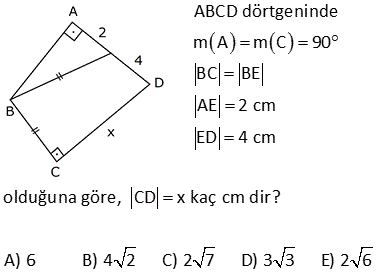

Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Çıkmış Sorular İçin Tıklayınız.
Abone olarak daha fazla sayıda soru sorabilirsiniz. Abone olmak için Tıklayın.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Not: Bu sitede yayınlanan çözümler, tamamen bu site için hazırlanmıştır. İzinsiz olarak yayınlanıp, çoğaltılması yasaktır.
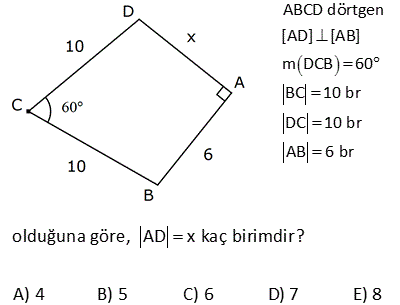
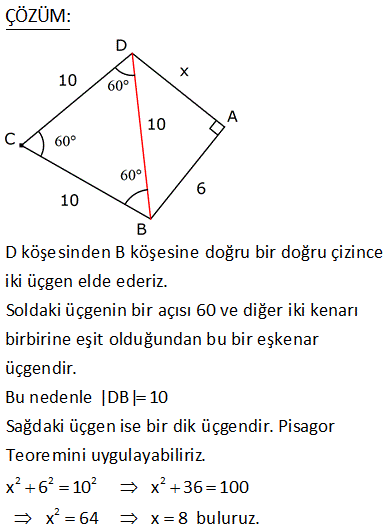
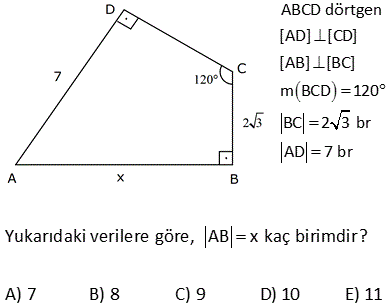
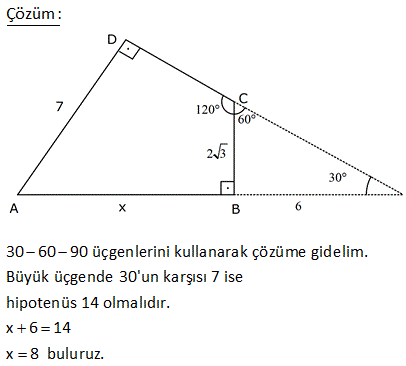
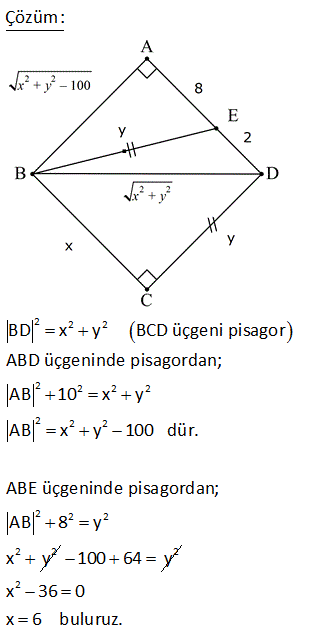
ABCD dörtgen [AD] [AB] m DCB 60 BC 10 br DC 10 br AB 6 br olduğuna göre, AD x kaç birimdir? A) 4 B) 5 C) 6 D) 7 E) 8 ÇÖZÜM: D köşesinden B köşesine doğru bir doğru çizince iki üçgen elde ederiz. Soldaki üçgenin bir açısı 60 ve diğer iki kenarı birbirine eşit olduğundan bu bir eşkenar üçgendir. Bu nedenle |DB| 10 Sağdaki üçge 2 2 2 2 2 n ise bir dik üçgendir. Pisagor Teoremini uygulayabiliriz. x 6 10 x 36 100 x 64 x 8 buluruz. 2 ABCD dörtgen [AD] [CD] [AB] [BC] m BCD 120 BC 2 3 br AD 7 br Yukarıdaki verilere göre, AB x kaç birimdir? A) 7 B) 8 C) 9 D) 10 E) 11 30 60 90 üçgenlerini kullanarak çözüme gidelim. Büyük üçgende 30’un karşısı 7 ise hipotenüs 14 olmalıdır. x 6 14 x 8 buluruz. 5 ABCD dörtgen, [AD] [CD], m BCE 45 m ECA 45 BE 2. AE AD DF CF 3 br ise, BF kaç br dir? A) 12 B) 13 C) 14 D) 15 E) 16 ADC üçgeninde pisagordan; AC 3 5 bulunur. AE x ve BE 2x tir. Açıortaya göre; BC 2.3 5 6 5 olmalıdır. ADC üçgeninde alan fomüllerinden; DH .3 5 3.6 6 DH tir. 2 2 5 DH 3 CT tir. 2 5 CFT üçgeninde pisagord 2 2 2 2 6 an FT tir. 5 BFT üçgeninde pisagordan; 3 6 BF 6 5 5 5 BF 180 2 6 5 3 5 2 2 2 9 36 5 5 9 36 BF 180 36 5 5 45 BF 180 36 5 BF 180 36 9 225 BF 15 bulunur. 27 ABCD dörtgen, m ABC 60 AB BC 6 cm DC 10 cm ABCD dörtgeninin alanının en büyük değeri için AD x kaç cm dir? A) 6 B) 4 3 C) 8 D) 97 E) 2 34 90 olmalı 2 2 ABC bir eşkenar üçgendir. AC 6 cm olur. A(ACD) en büyük olabilmesi için, m(ACD) 90 olmalıdır. 1 A(ACD) AC DC sin ACD 2 ACD üçgeninde pisagordan; x 36 100 x 136 x 136 4.34 2 34 buluruz. 30 Şekildeki verilere göre, AB x kaç birimdir? Şekildeki gibi ABE üçgenini oluşturalım. m(E) 180 A B 180 60 30 90 dir. m(EDC) 180 150 30 dir. EDC üçgeni bir 30 -60 -90 üçgenidir. EC a ise ED a 3 birimdir. ABE üçgeni de bir 30 -60 -90 üçgenidir. 3. EA E B olmalıdır. 3 5 a 3 a 8 3 3 3 5 3 3a a 8 3 2a 3 3 a dir. 2 3 3 9 19 O halde; EA 5 a 3 5 3 5 dir. 2 2 2 x uzunluğu, 90 nin karşısında olduğuna göre; 19 x 2 EA 2 19 dur. 2 52 ABCD dörtgen [AB] [AD] [BC] [CD] AE 8 cm ED 2 cm BE DC Verilenlere göre, BC x kaç cm dir? A) 6 B) 7 C) 8 D) 9 E) 10 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 BD x y BCD üçgeni pisagor ABD üçgeninde pisagordan; AB 10 x y AB x y 100 dür. ABE üçgeninde pisagordan; AB 8 y x y 2100 64 y 2 x 36 0 x 6 buluruz. 57 ABCD dörtgen AD 8 cm DC 10 cm [AD] [AB] [DC] [BC] m ADC 60 olduğuna göre, AB kaç cm dir? A) 5 3 B) 4 3 C) 3 3 D) 2 3 E) 3 C’den K’ya şekildeki gibi dikme çizelim. DKC üçgeni 30 -60 -90 üçgeni olduğundan DK 5 cm olur. Hipotenüsün yarısı KC 5 3 cm olur. KA 8 5 3 cm kalır. B’den L’ye dikme indirelim. BLC üçgeni de bir 30 -60 -90 üçg enidir. LB 3 ise LC 3 cm dir. O halde; KL 5 3 3 4 3 cm AB KL 4 3 buluruz. 61 ABCD dörtgeninde m A m C 90 BC BE AE 2 cm ED 4 cm olduğuna göre, CD x kaç cm dir? A) 6 B) 4 2 C) 2 7 D) 3 3 E) 2 6 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 ABE üçgeninde pisagor teoremi uygulayalım. AB AE y AB 2 y AB y 4 tür. ABD üçgeninde pisagor teoremi uygulayalım. AB AD BD y 4 6 BD y 4 36 BD y 32 BD dir. BCD üçgeninde pisagor teoremi uygulay 2 2 2 2 2 2 2 2 alım. BC CD BD y x BD dir. Son iki denlem de BD sine eşit olduğundan ikisini birbirine eşitleyelim. y 2 32 y 2 2 x x 32 x 32 4 2 bulunur. 72

