Soru Sor sayfası kullanılarak Dörtgenler konusu altında Dörtgende Orta Taban Birleştirerek Üçgen-Paralelkenar Oluşturma ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
2.SORU
3.SORU
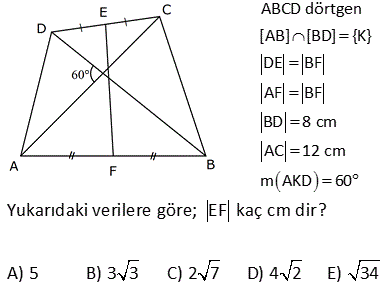

4.SORU
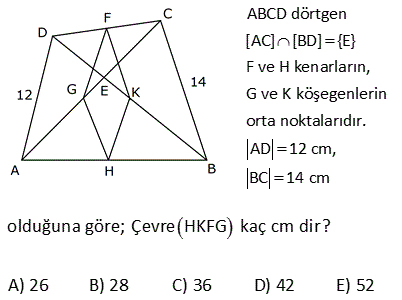

5.SORU
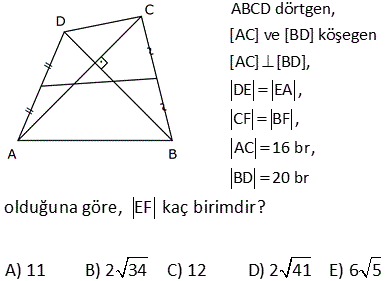
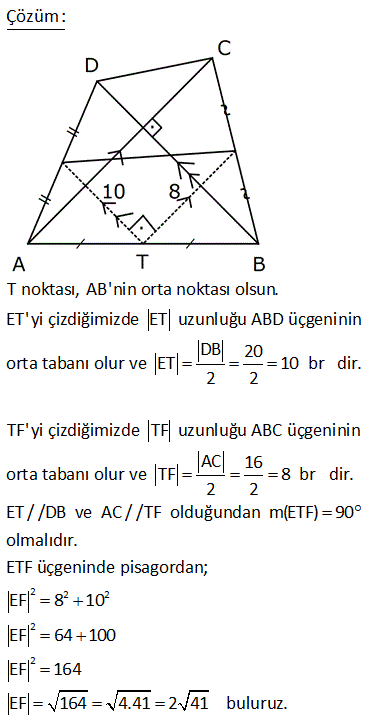
6.SORU
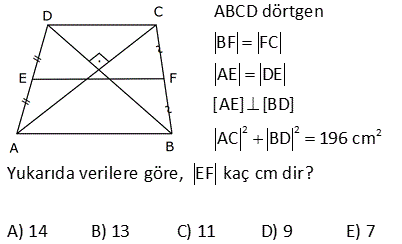
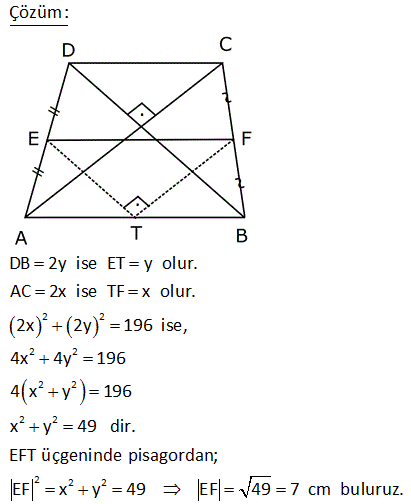
7.SORU
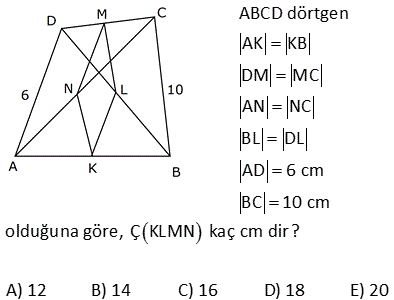

8.SORU
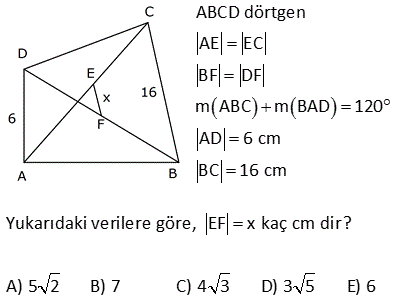

9.SORU
10.SORU

Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Çıkmış Sorular İçin Tıklayınız.
Abone olarak daha fazla sayıda soru sorabilirsiniz. Abone olmak için Tıklayın.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Not: Bu sitede yayınlanan çözümler, tamamen bu site için hazırlanmıştır. İzinsiz olarak yayınlanıp, çoğaltılması yasaktır.
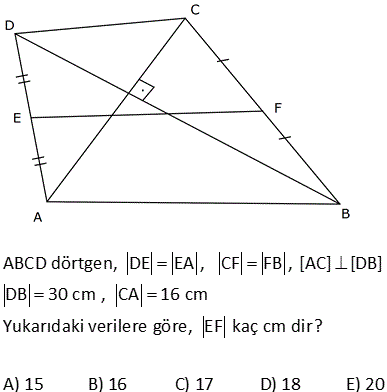
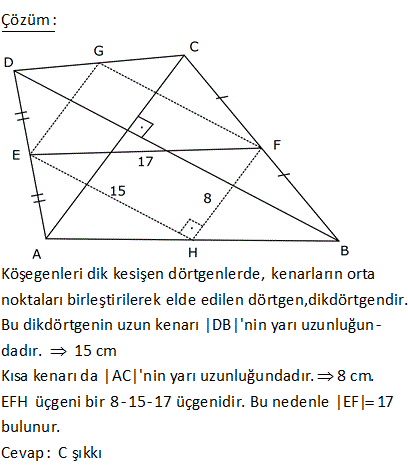
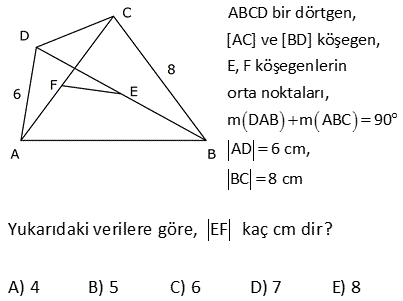
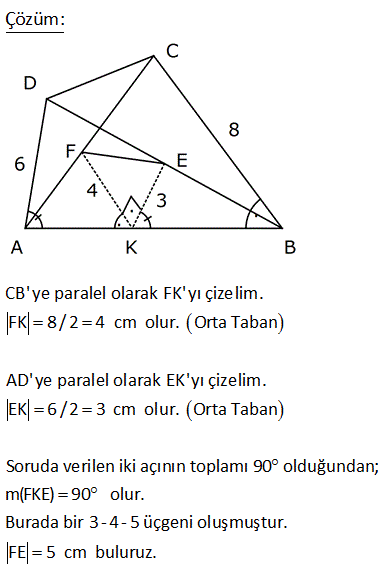
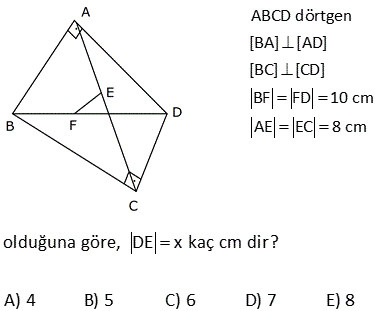
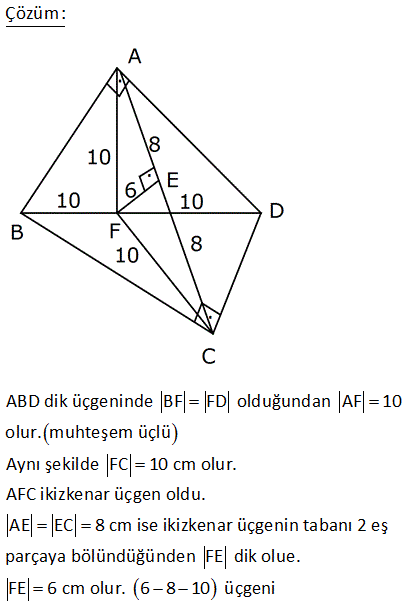
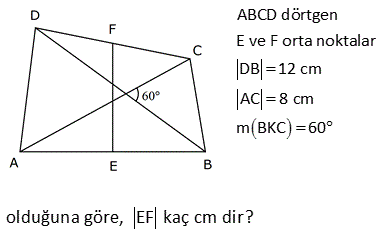
ABCD dörtgen, DE EA , CF FB , [AC] [DB] DB 30 cm , CA 16 cm Yukarıdaki verilere göre, EF kaç cm dir? A) 15 B) 16 C) 17 D) 18 E) 20 Köşegenleri dik kesişen dörtgenlerde, kenarların orta noktaları birleştirilerek elde edilen dörtgen, dikdörtgendir. Bu dikdörtgenin uzun kenarı |DB|’nin yarı uzunluğun – dadır. 15 cm Kısa kenarı da |AC|’ nin yarı uzunluğundadır. 8 cm. EFH üçgeni bir 8 -15-17 üçgenidir. Bu nedenle |EF| 17 bulunur. Cevap: C şıkkı 7 ABCD bir dörtgen, [AC] ve [BD] köşegen, E, F köşegenlerin orta noktaları, m DAB m ABC 90 AD 6 cm, BC 8 cm Yukarıdaki verilere göre, EF kaç cm dir? A) 4 B) 5 C) 6 D) 7 E) 8 CB’ye paralel olarak FK’yı çizelim. FK 8 / 2 4 cm olur. Orta Taban AD’ye paralel olarak EK’yı çizelim. EK 6 / 2 3 cm olur. Orta Taban Soruda verilen iki açının toplamı 90 olduğundan; m(FKE) 90 olur. B urada bir 3- 4 – 5 üçgeni oluşmuştur. FE 5 cm buluruz. 34 ABCD dörtgen [AB] [BD] {K} DE BF AF BF BD 8 cm AC 12 cm m AKD 60 Yukarıdaki verilere göre; EF kaç cm dir? A) 5 B) 3 3 C) 2 7 D) 4 2 E) 34 BD ye paralel olarak, ER’ yi çizelim. BD ER 4 birim olur. Orta taban 2 AC ye paralel olarak, FR’ yi çizelim. AC FR 6 birim olur. Orta taban 2 m(ERF) m(AKD) 60 dir. ERF üçgeninde, kenarlar 4 ve 6 aradaki aç 2 2 2 2 ı da 60 olduğundan EF yi bulabiliriz. Biz kosinüs teoremini kullanacağız. Bu bilinmiyorsa 60’ın karşısına dik indirilip, Sonra da pisagor teoremi ile de bulunabilir EF 4 6 2.4.6cos60 EF 16 36 48c 2 2 1 os60 cos60 2 EF 52 24 EF 28 EF 2 7 buluruz. 41 ABCD dörtgen [AC] [BD] {E} F ve H kenarların, G ve K köşegenlerin orta noktalarıdır. AD 12 cm, BC 14 cm olduğuna göre; ÇevreHKFG kaç cm dir? A) 26 B) 28 C) 36 D) 42 E) 52 GF uzunluğu, ADC üçgeninin orta tabanıdır. AD 12 Bu sebeple GF 6 cm olur. 2 2 Aynı şekilde; GH uzunluğu, ABC üçgeninin orta tabanıdır. BC 14 Bu sebeple GH 7 cm olur. 2 2 Bir dörtgende, köşegenlerin orta nokt aları ile birleştirilerek oluşan şekil, bir paralelkenardır. Bu paralelkenarın iki kenarı 6 ve 7 cm ise; karşısındaki kenarlar da 6 ve 7 cm olur. Buna göre; Ç(HKFG) 2 6 7 2.13 26 cm buluruz. 42 ABCD dörtgen, [AC] ve [BD] köşegen [AC] [BD], DE EA , CF BF , AC 16 br, BD 20 br olduğuna göre, EF kaç birimdir? A) 11 B) 2 34 C) 12 D) 2 41 E) 6 5 T noktası, AB’nin orta noktası olsun. ET’ yi çizdiğimizde ET uzunluğu ABD üçgeninin DB 20 orta tabanı olur ve ET 10 br dir. 2 2 TF’ yi çizdiğimizde TF uzunluğu ABC üçgeninin AC 16 orta tabanı olur ve TF 2 2 2 2 2 2 2 8 br dir. ET / /DB ve AC / /TF olduğundan m(ETF) 90 olmalıdır. ETF üçgeninde pisagordan; EF 8 10 EF 64 100 EF 164 EF 164 4.41 2 41 buluruz. 44 2 2 2 ABCD dörtgen BF FC AE DE [AE] [BD] AC BD 196 cm Yukarıda verilere göre, EF kaç cm dir? A) 14 B) 13 C) 11 D) 9 E) 7 2 2 2 2 2 2 2 2 2 2 2 DB 2y ise ET y olur. AC 2x ise TF x olur. 2x 2y 196 ise, 4x 4y 196 4 x y 196 x y 49 dir. EFT üçgeninde pisagordan; EF x y 49 EF 49 7 cm buluruz. 56 ABCD dörtgen AK KB DM MC AN NC BL DL AD 6 cm BC 10 cm olduğuna göre, ÇKLMN kaç cm dir? A) 12 B) 14 C) 16 D) 18 E) 20 MN uzunluğu, ADC üçgeninin orta tabanıdır. AD 6 Bu sebeple MN 3 cm olur. 2 2 Aynı şekilde; NK uzunluğu, ABC üçgeninin orta tabanıdır. BC 10 Bu sebeple NK 5 cm olur. 2 2 Bir dörtgende, köşegenlerin orta noktaları ile birleştirilerek oluşan şekil, bir paralelkenardır. Bu paralelkenarın iki kenarı 3 ve 5 cm ise; karşısındaki kenarlar da 3 ve 5 cm olur. Buna göre; Ç(KLMN) 2 3 5 2.816 cm buluruz. 69 ABCD dörtgen AE EC BF DF m ABC m BAD 120 AD 6 cm BC 16 cm Yukarıdaki verilere göre, EF x kaç cm dir? A) 5 2 B) 7 C) 4 3 D) 3 5 E) 6 T noktası AB doğrusunun orta noktası olsun. TF uzunluğu ABD üçgeninin orta tabanıdır. 6 TF 3 tür. 2 ET uzunluğu da ABC üçgeninin orta tabanıdır. 16 ET 8 dir. 2 m(BAD) m(BTF) ve m(ABC) m(ATE) olduğund 2 2 2 01.Şub 2 2 an m(BTF) m(ATE) 120 dir. m(ETF) 60 kalır. Kosinüs teoreminden x uzunluğunu bulabiliriz. Bu bilinmiyorsa 30 -60 -90 üçgenleri oluşturarak da çözülebilir. x 8 3 2.3.8.cos60 x 64 9 24 x 49 x 7 buluruz. 71 ABCD dörtgen [BA] [AD] [BC] [CD] BF FD 10 cm AE EC 8 cm olduğuna göre, DE x kaç cm dir? A) 4 B) 5 C) 6 D) 7 E) 8 ABD dik üçgeninde BF FD olduğundan AF 10 olur. muhteşem üçlü Aynı şekilde FC 10 cm olur. AFC ikizkenar üçgen oldu. AE EC 8 cm ise ikizkenar üçgenin tabanı 2 eş parçaya bölündüğünden FE dik olue. FE 6 cm olur . 6810 üçgeni 74 ABCD dörtgen E ve F orta noktalar DB 12 cm AC 8 cm m BKC 60 olduğuna göre, EF kaç cm dir? AD’nin orta noktası H olsun. HF uzunluğu AC’nin yarısıdır. HF uzunluğu ADC üçgeninin orta tabanıdır. 8 HF 4 cm dir. 2 HE uzunluğu DB’nin yarısıdır. HE uzunluğu ADB üçgeninin orta tabanıdır. 12 HE 6 cm dir 2 2 2 2 2 . HFE üçgeninde kosinüs teoremini uygulayarak EF ‘ yi bulabiliriz. EF 4 6 2.4.6.cos60 EF 16 36 2 1 4 6 2 2 2 EF 16 36 24 EF 28 EF 2 7 cm buluruz.

