Soru Sor sayfası kullanılarak Dörtgenler konusu altında Dörtgende Alan Bulma ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
2.SORU
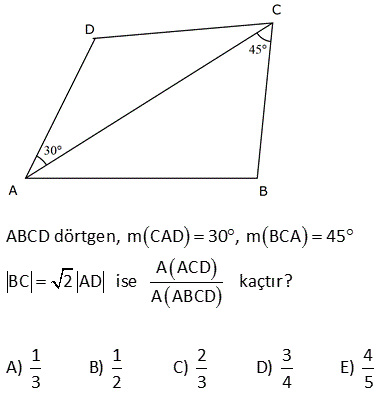

3.SORU
4.SORU


5.SORU
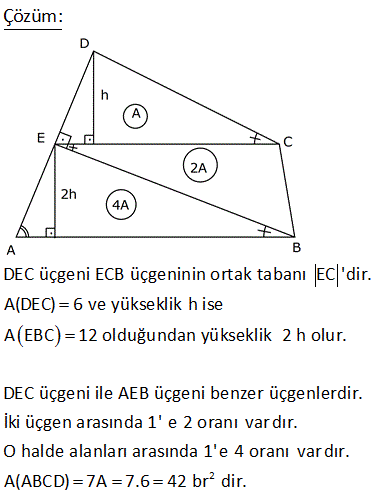
6.SORU

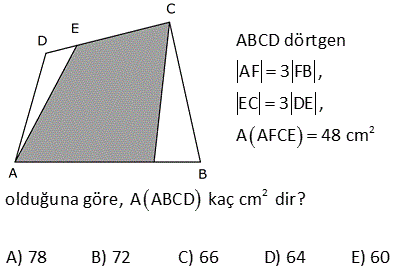
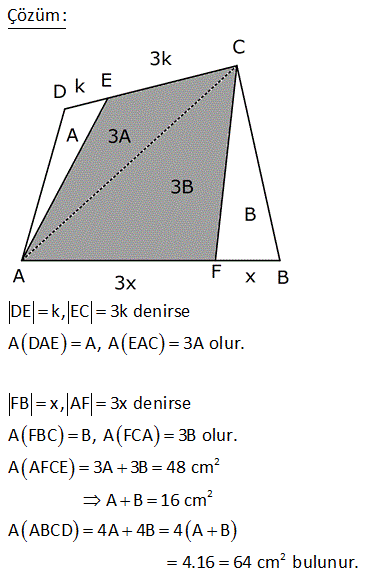
7.SORU

8.SORU
9.SORU

10.SORU
11.SORU
12.SORU
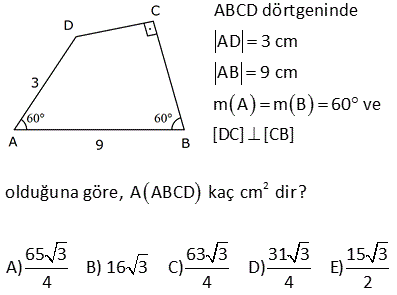
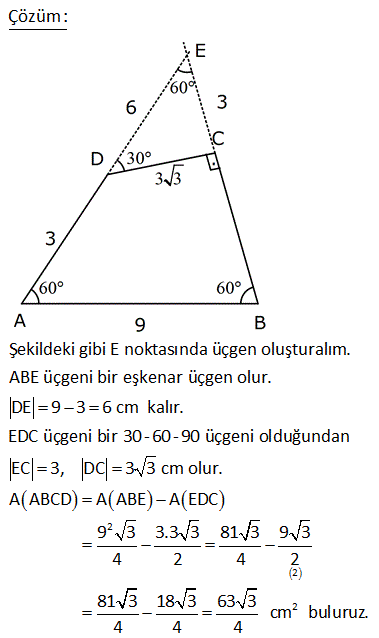
13.SORU
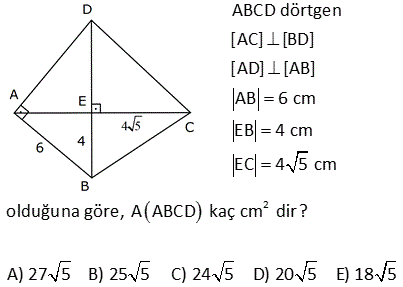
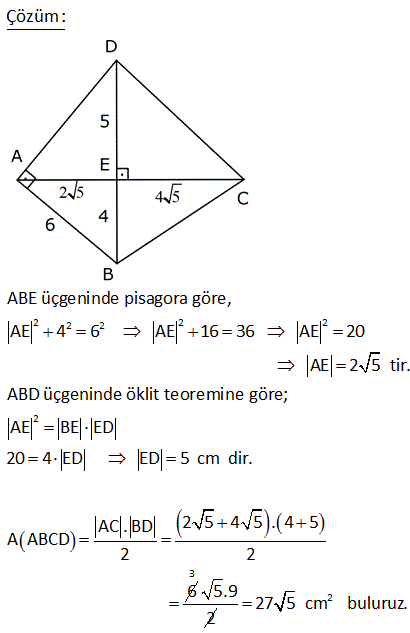
14.SORU
Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Çıkmış Sorular İçin Tıklayınız.
Abone olarak daha fazla sayıda soru sorabilirsiniz. Abone olmak için Tıklayın.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Not: Bu sitede yayınlanan çözümler, tamamen bu site için hazırlanmıştır. İzinsiz olarak yayınlanıp, çoğaltılması yasaktır.
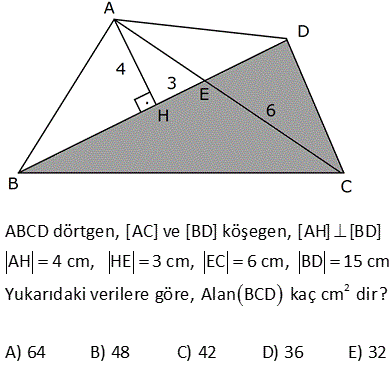
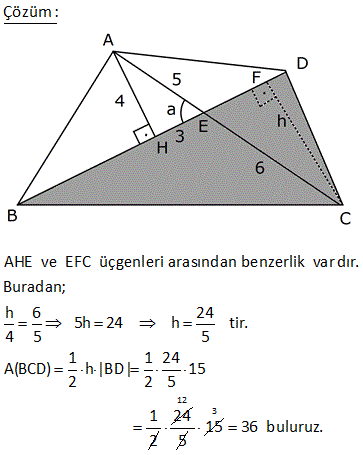
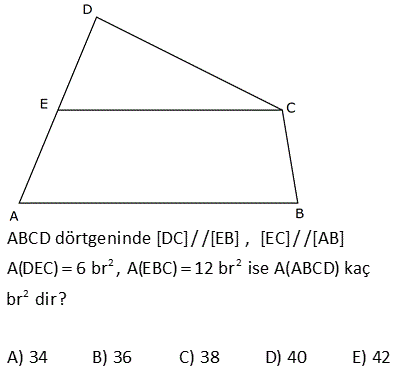
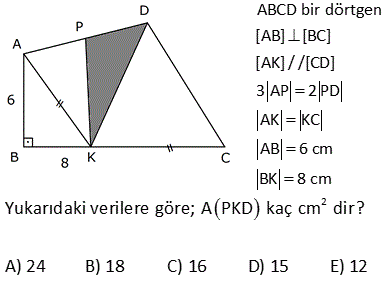
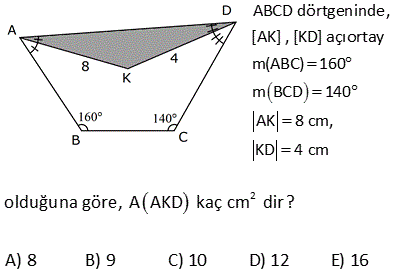
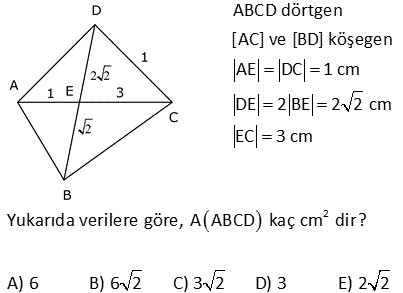
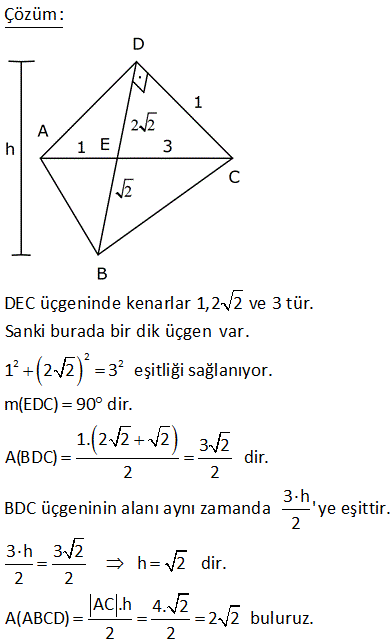
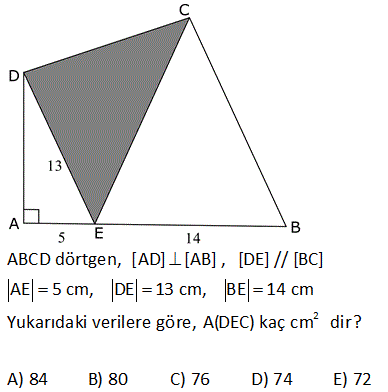
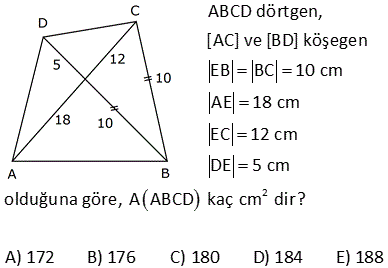
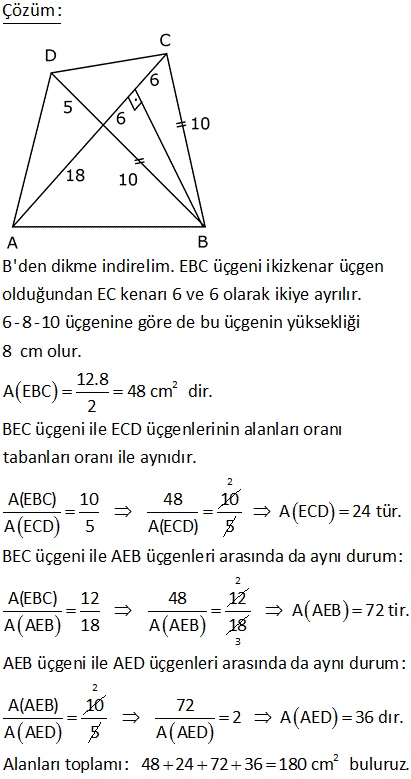
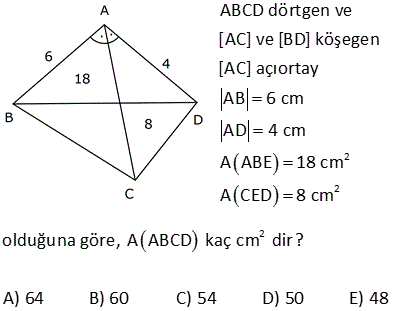
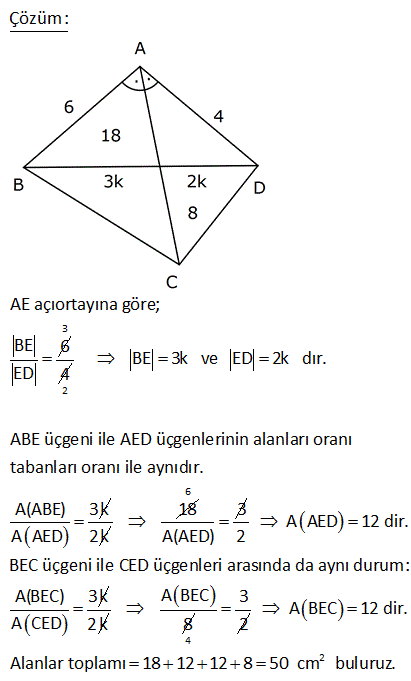
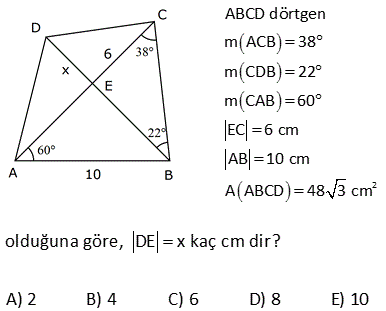
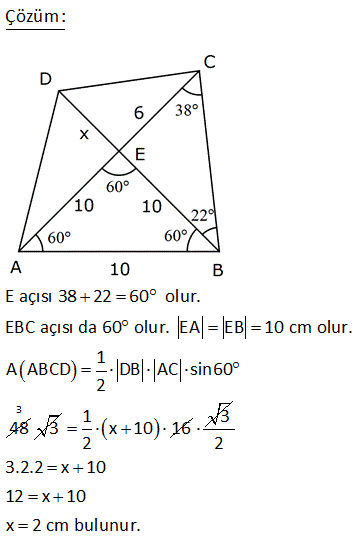
2 ABCD dörtgen, [AC] ve [BD] köşegen, [AH] [BD] AH 4 cm, HE 3 cm, EC 6 cm, BD 15 cm Yukarıdaki verilere göre, Alan BCD kaç cm dir? A) 64 B) 48 C) 42 D) 36 E) 32 AHE ve EFC üçgenleri arasından benzerlik vardır. Buradan; h 6 24 5h 24 h tir. 4 5 5 1 1 24 A(BCD) h |BD| 15 2 2 5 1 2 24 12 5 15 3 36 buluruz. 8 ABCD dörtgen, m CAD 30 , m BCA 45 A ACD BC 2 AD ise kaçtır? A ABCD 1 1 2 3 4 A) B) C) D) E) 3 2 3 4 5 B ve D köşelerinden AC kçşegenine yükseklikler indirelim. |BE| x dersek; 45- 45-90 üçgeninden |BC| x 2 olur. |BC| 2|AD| |AD| x olur. x 30 60 90 üçgeninden |DF| dir. 2 1 x x Buna göre; A(ACD) y 2 2 y tür. A diyelim 4 1 xy A(ABC) x y dir. 2A our. 2 2 Tüm alan 3A dır. Buna göre; A(ACD) A 1 buluruz. A(ABCD) 3A 3 10 2 2 2 ABCD dörtgeninde [DC] / /[EB] , [EC] / /[AB] A(DEC) 6 br , A(EBC) 12 br ise A(ABCD) kaç br dir? A) 34 B) 36 C) 38 D) 40 E) 42 DEC üçgeni ECB üçgeninin ortak tabanı EC ‘dir. A(DEC) 6 ve yükseklik h ise A EBC 12 olduğundan yükseklik 2 h olur. DEC üçgeni ile AEB üçgeni benzer üçgenlerdir. İki üçgen arasında 1’ e 2 oranı var dır. O h 2 alde alanları arasında 1’e 4 oranı var dır. A(ABCD) 7A 7.6 42 br dir. 15 ABC bir üçgen AE 4 cm BC 10 cm m BDA 60 2 Yukarıdaki verilere göre, ABEC dörtgeninin alanı kaç cm dir? A) 6 3 B) 14 C) 10 2 D) 16 E) 10 3 BC uzunluğunu 2x ve 2y şeklinde parçalayalım. ABD üçgeninde 90 nin karşısında 2x var sa 60 nin karşısında x 3 olur. AEC üçgeninde 90 nin karşısında 2y var sa 60 nin karşısında y 3 olur. Üçgenlerin alanlar 2 10 ını hesaplayıp toplayalım. 2x 2y 10 x 3.4 y 3.4 2x 3 2y 3 2 2 3 2x 2y 10 3 cm bulunur. 17 2 ABCD dörtgen AF 3 FB , EC 3 DE , A AFCE 48 cm 2 olduğuna göre, A ABCD kaç cm dir? A) 78 B) 72 C) 66 D) 64 E) 60 2 2 2 DE k, EC 3k denirse A DAE A, A EAC 3A olur. FB x, AF 3x denirse A FBC B, A FCA 3B olur. A AFCE 3A 3B 48 cm A B 16 cm A ABCD 4A 4B 4 A B 4.16 64 cm bulunur. 70 ABCD bir dörtgen [AB] [BC] [AK] / /[CD] 3 AP 2 PD AK KC AB 6 cm BK 8 cm 2 Yukarıdaki verilere göre; A PKD kaç cm dir? A) 24 B) 18 C) 16 D) 15 E) 12 K’dan F’ye bir dik indirelim. AK / /CD olduğundan m(AKB) m(FCK) dır. AK KC olduğundan ABK üçgeni ile KFC üçgeni eş üçgenlerdir. KF 6 cm olur. AK / /CD olduğundan; ADK üçgeninin yüksekliği KF 6’ya 2 eşittir. 10.Haz A(ADK)= 30 cm dir. 2 30 30 A(PKD)= 3x 2x 3x 5x .3 x 6.318 cm2 dir. 40 ABCD dörtgeninde, [AK] , [KD] açıortay m(ABC) 160 m BCD 140 AK 8 cm, KD 4 cm 2 olduğuna göre, A AKD kaç cm dir? A) 8 B) 9 C) 10 D) 12 E) 16 30 Dörtgenin iç açıları toplamı 360 dir. 2x 2y 160 140 360 olmalıdır. 2 x y 300 360 2 x y 60 x y 30 dir. AKD üçgenin iç açıları toplamından; m(AKD) x y 180 m(AKD) 150 dir. Sinüs alan formülünden A(AKD) bu 01.Şub lunabilir. 1 1 1 32 A(AKD) 4 8 sin150 32 8 buluruz. 2 2 2 4 Sinüs alan formülü bilinmiyorsa, bir üçgen çizip hesaplama yapmak gerekiyor. 48 ABCD dörtgen [AC] ve [BD] köşegen AE DC 1 cm DE 2 BE 2 2 cm EC 3 cm 2 Yukarıda verilere göre, A ABCD kaç cm dir? A) 6 B) 6 2 C) 3 2 D) 3 E) 2 2 2 2 2 DEC üçgeninde kenarlar 1,2 2 ve 3 tür. Sanki burada bir dik üçgen var. 1 2 2 3 eşitliği sağlanıyor. m(EDC) 90 dir. 1. 2 2 2 3 2 A(BDC) dir. 2 2 3 h BDC üçgeninin alanı aynı zamanda ‘ ye eşittir. 2 3 h 3 2 2 2 h 2 dir. AC .h 4. 2 A(ABCD) 2 2 buluruz. 2 2 55 2 ABCD dörtgen, [AD] [AB] , [DE] // [BC] AE 5 cm, DE 13 cm, BE 14 cm Yukarıdaki verilere göre, A(DEC) kaç cm dir? A) 84 B) 80 C) 76 D) 74 E) 72 Şekildeki gibi BFE dik üçgenini oluşturalım. DAE üçgeni ile BFE üçgeni benzerdir. Açıları aynı h 14 14.12 h tür. 12 13 13 13 13.h A(DEC) 2 14 7 .12 13 2 7.12 84 buluruz. 58 ABCD dörtgen, [AC] ve [BD] köşegen EB BC 10 cm AE 18 cm EC 12 cm DE 5 cm 2 olduğuna göre, A ABCD kaç cm dir? A) 172 B) 176 C) 180 D) 184 E) 188 2 B’den dikme indirelim. EBC üçgeni ikizkenar üçgen olduğundan EC kenarı 6 ve 6 olarak ikiye ayrılır. 6 -8 -10 üçgenine göre de bu üçgenin yüksekliği 8 cm olur. 12.Ağu A EBC 48 cm dir. 2 BEC üçgeni ile ECD üçge nlerinin alanları oranı tabanları oranı ile aynıdır. A(EBC) 10 48 10 A ECD 5 A(ECD) 2 5 A ECD 24 tür. BEC üçgeni ile AEB üçgenleri arasında da aynı durum: A(EBC) 12 48 12 A AEB 18 A AEB 2 18 3 A AEB 72 tir. AEB üçgeni ile AED üçgenleri arasında da aynı durum: A(AEB) 10 A AED 2 5 2 72 2 A AED 36 dır. A AED Alanları toplamı : 48 24 72 36 180 cm buluruz. 64 2 2 ABCD dörtgen ve [AC] ve [BD] köşegen [AC] açıortay AB 6 cm AD 4 cm A ABE 18 cm A CED 8 cm 2 olduğuna göre, A ABCD kaç cm dir? A) 64 B) 60 C) 54 D) 50 E) 48 AE açıortayına göre; BE 6 ED 3 4 2 BE 3k ve ED 2k dır. ABE üçgeni ile AED üçgenlerinin alanları oranı tabanları oranı ile aynıdır. A(ABE) 3k A AED 2k 18 6 3 A(AED) A AED 12 dir. 2 BEC üçgeni ile CED üçgenleri arasında da aynı durum: A(BEC) 3k A CED 2k ABEC 8 4 3 2 2 A BEC 12 dir. Alanlar toplamı 18 12 12 8 50 cm buluruz. 65 ABCD dörtgeninde AD 3 cm AB 9 cm m A m B 60 ve [DC] [CB] 2 olduğuna göre, A ABCD kaç cm dir? 65 3 63 3 31 3 15 3 A) B) 16 3 C) D) E) 4 4 4 2 2 Şekildeki gibi E noktasında üçgen oluşturalım. ABE üçgeni bir eşkenar üçgen olur. DE 9 3 6 cm kalır. EDC üçgeni bir 30 -60 -90 üçgeni olduğundan EC 3, DC 3 3 cm olur. A ABCD A ABE A EDC 9 3 4 2 2 3.3 3 81 3 9 3 2 4 2 81 3 18 3 63 3 cm buluruz. 4 4 4 67 ABCD dörtgen [AC] [BD] [AD] [AB] AB 6 cm EB 4 cm EC 4 5 cm 2 olduğuna göre, A ABCD kaç cm dir? A) 27 5 B) 25 5 C) 24 5 D) 20 5 E) 18 5 2 2 2 2 2 2 ABE üçgeninde pisagora göre, AE 4 6 AE 16 36 AE 20 AE 2 5 tir. ABD üçgeninde öklit teoremine göre; AE BE ED 20 4 ED ED 5 cm dir. AC . BD 2 5 4 5 . 4 5 A ABCD 2 2 6 3 05.Eyl 2 2 27 5 cm buluruz. 68 2 ABCD dörtgen m ACB 38 m CDB 22 m CAB 60 EC 6 cm AB 10 cm A ABCD 48 3 cm olduğuna göre, DE x kaç cm dir? A) 2 B) 4 C) 6 D) 8 E) 10 E açısı 38 22 60 olur. EBC açısı da 60 olur. EA EB 10 cm olur. 1 A ABCD DB AC sin60 2 48 3 3 1 x 10 16 2 3 2 3.2.2 x 10 12 x 10 x 2 cm bulunur. 73


çok zor ln
yapabilen varsa yazsın bana ser alnından öpücem