Soru Sor sayfası kullanılarak Dörtgenler konusu altında Dörtgende Açı Bulma ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
2.SORU
3.SORU
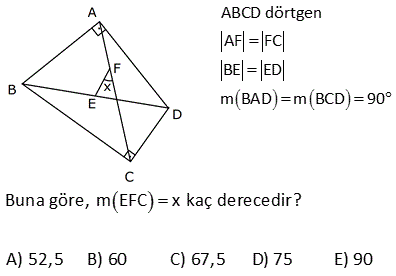

4.SORU
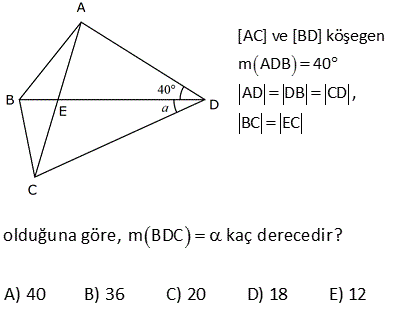

5.SORU
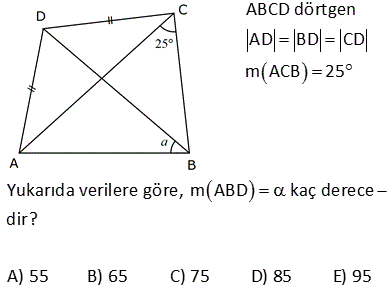
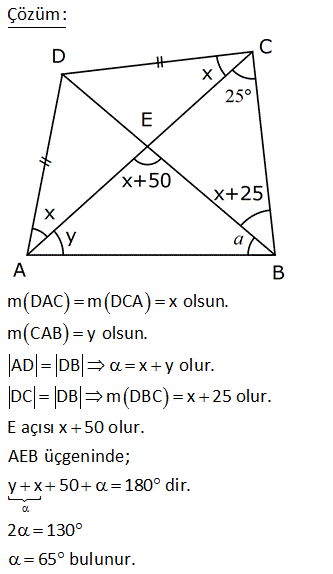
6.SORU
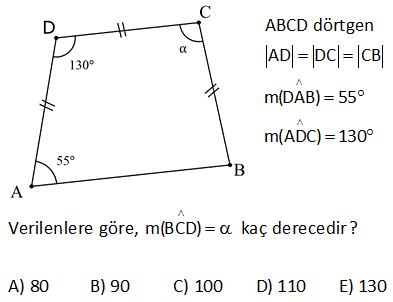
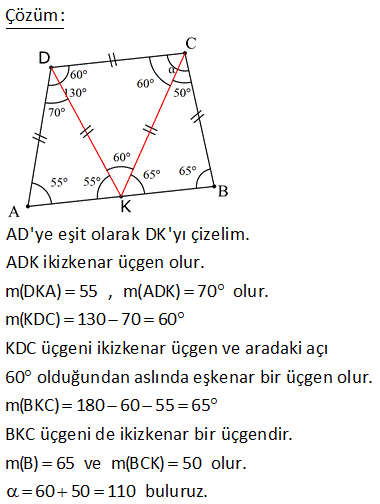
7.SORU
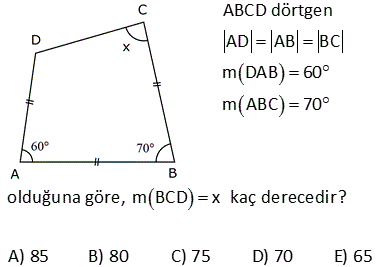

8.SORU
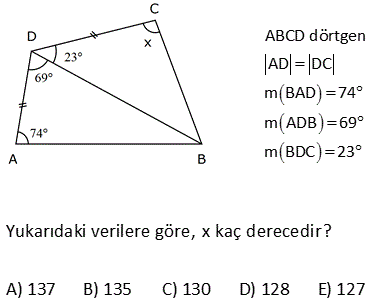

9.SORU
Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Çıkmış Sorular İçin Tıklayınız.
Abone olarak daha fazla sayıda soru sorabilirsiniz. Abone olmak için Tıklayın.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Not: Bu sitede yayınlanan çözümler, tamamen bu site için hazırlanmıştır. İzinsiz olarak yayınlanıp, çoğaltılması yasaktır.
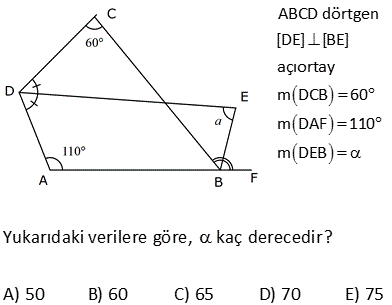
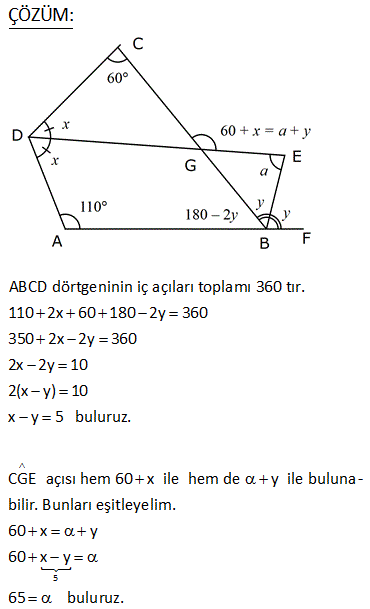
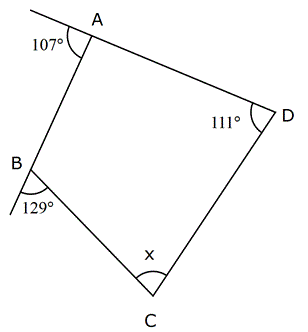
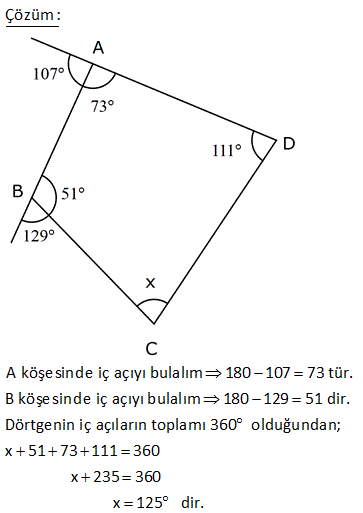
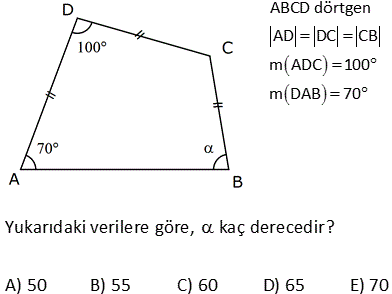
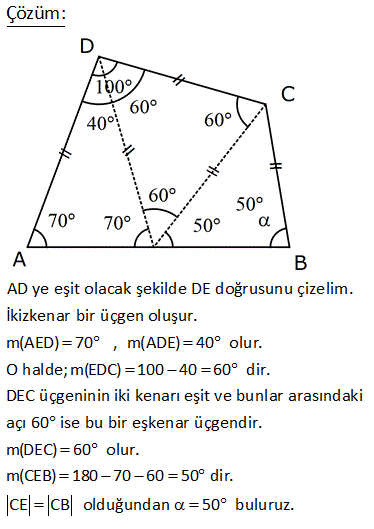
ABCD dörtgen [DE] [BE] açıortay m DCB 60 m DAF 110 m DEB Yukarıdaki verilere göre, kaç derecedir? A) 50 B) 60 C) 65 D) 70 E) 75 ÇÖZÜM: ABCD dörtgeninin iç açıları toplamı 360 tır. 110 2x 60 180 2y 360 350 2x 2y 360 2x 2y 10 2(x y) 10 x y 5 buluruz. CGE açısı hem 60 x ile hem de y ile bulunabilir. Bunları eşitleyelim. 60 x y 60 x 5 y 65 buluruz. 3 A köşesinde iç açıyı bulalım 180 107 73 tür. B köşesinde iç açıyı bulalım 180 129 51 dir. Dörtgenin iç açıların toplamı 360 olduğundan; x 51 73 111 360 x 235 360 x125 dir. 11 ABCD dörtgen AF FC BE ED m BAD m BCD 90 Buna göre, mEFC x kaç derecedir? A) 52,5 B) 60 C) 67,5 D) 75 E) 90 Karşılıklı iki açısının toplamı 180 olan dörtgenler kirişler dörtgenidir. Bu dörtgen de BD çaplı bir çemberin içine çizilmiştir. Çapı gören çevre açı 90 dir. E noktası, BD’ni orta noktası olduğundan çemberin merkezidir. F noktası da AC’nin orta noktasıymış. Sadece merkezden kirişe inilen dikme, kirişi iki eş parçaya ayrırır. Bu sebeple m(EFC) 90 olmalıdır. 37 [AC] ve [BD] köşegen m ADB 40 AD DB CD , BC EC olduğuna göre, mBDC kaç derecedir? A) 40 B) 36 C) 20 D) 18 E) 12 m(ADB) 40 ve AD DB ise 180 40 140 m(BAD) m(ABD) 70 dir. 2 2 m(CBD) x olsun. BC EC olduğundan m(BEC) x tir. BCE üçgeninin iç açıları toplamı 180 dir. m(BCE) 180 x x 180 2x olmalıdır. ABC üçgeninin i ç açıları toplamı 180 dir. m(BAC) 180 70 x 180 2x x 70 olur. BD DC olduğundan m(BCD) x tir. m(ECD) x 180 2x 3x 180 dir. AD DC olduğundan m(DAC) 3x 180 dir. m(BAD) 70 ise; x 70 3x 180 70 4x 250 70 4x 320 x 80 dir. BCD üçgeninin iç açıları toplamı 180 dir. x x 180 80 80 180 180 160 20 buluruz. 46 ABCD dörtgen AD BD CD m ACB 25 Yukarıda verilere göre, mABD kaç derece dir? A) 55 B) 65 C) 75 D) 85 E) 95 m DAC m DCA x olsun. m CAB y olsun. AD DB x y olur. DC DB m DBC x 25 olur. E açısı x 50 olur. AEB üçgeninde; y x 50 180 dir. 2 130 65 bulunur. 53 ABCD dörtgen AD DC CB m(DAB) 55 m(ADC) 130 Verilenlere göre, m(BCD) kaç derecedir? A) 80 B) 90 C) 100 D) 110 E) 130 AD’ye eşit olarak DK’ yı çizelim. ADK ikizkenar üçgen olur. m(DKA) 55 , m(ADK) 70 olur. m(KDC) 130 70 60 kalır. KDC üçgeni ikizkenar üçgen ve aradaki açı 60 oldu – ğundan aslında eşkenar bir üçgen olu r. m(BKC) 180 60 55 65 kalır. BKC üçgeni de ikizkenar bir üçgendir. m(B) 65 ve m(BCK) 50 olur. 60 50 110 buluruz. 54 ABCD dörtgen AD AB BC m DAB 60 m ABC 70 olduğuna göre, mBCD x kaç derecedir? A) 85 B) 80 C) 75 D) 70 E) 65 DB doğrusunu çizelim. AD AB ve aralarındaki açı 60 olduğundan ABD üçgeninin diğer iç açıları 60’ar derece olur. Dolayısıyla ABD üçgeni eşkenar üçgendir. BC BD olduğundan m(BDC) x olur. m(CBD) 70 60 1 0 dir. BCD üçgeninin iç açıları toplamından; x x 10 180 2x 10 180 2x 170 x 85 buluruz. 62 ABCD dörtgen AD DC m BAD 74 m ADB 69 m BDC 23 Yukarıdaki verilere göre, x kaç derecedir? A) 137 B) 135 C) 130 D) 128 E) 127 m(DBA) 180 74 69 37 dir. m(BDE) 37 olacak şekilde DE doğrusunu çizelim. BDE üçgeni ikizkenar üçgen olur. m(DEA) 37 37 74 dir. O halde; AD DE olur. m EDC 37 23 60 dir. Ayrıca DE DC olduğundan bu b m BCE ‘ye eşit. ir eşkenar üçgen olmak zorundadır. Dolayısıyla EC EB olur. BEC ikizkenar üçgen olduğundan; m BCE m(CBE) 134 2m BCE 134 m BCE 67 dir. x 60 67 127 buluruz. 76 ABCD dörtgen AD DC CB m ADC 100 m DAB 70 Yukarıdaki verilere göre, kaç derecedir? A) 50 B) 55 C) 60 D) 65 E) 70 AD ye eşit olacak şekilde DE doğrusunu çizelim. İkizkenar bir üçgen oluşur. m(AED) 70 , m(ADE) 40 olur. O halde; m(EDC) 100 40 60 dir. DEC üçgeninin iki kenarı eşit ve bunlar arasındaki açı 60 ise bu bir eşkenar üçgendir. m(DEC) 60 olur. m(CEB) 180 70 60 50 dir. CE CB olduğundan 50 buluruz. 22

