Soru Sor sayfası kullanılarak Diziler konusu altında Sonsuz sayıda şekillerin alanları toplamı (üçgen,kare,dikdörtgen, çember) ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU

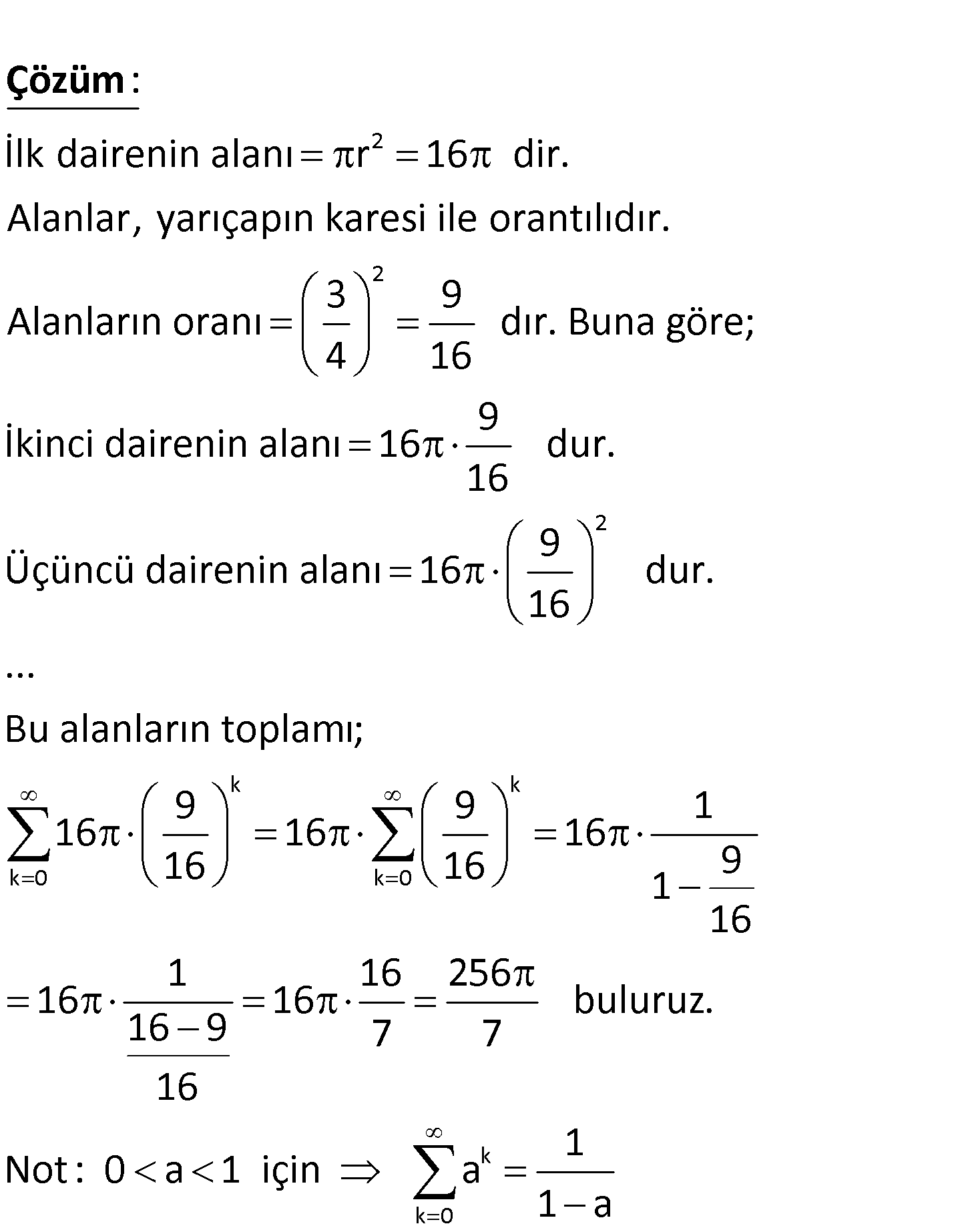
3.SORU


4.SORU

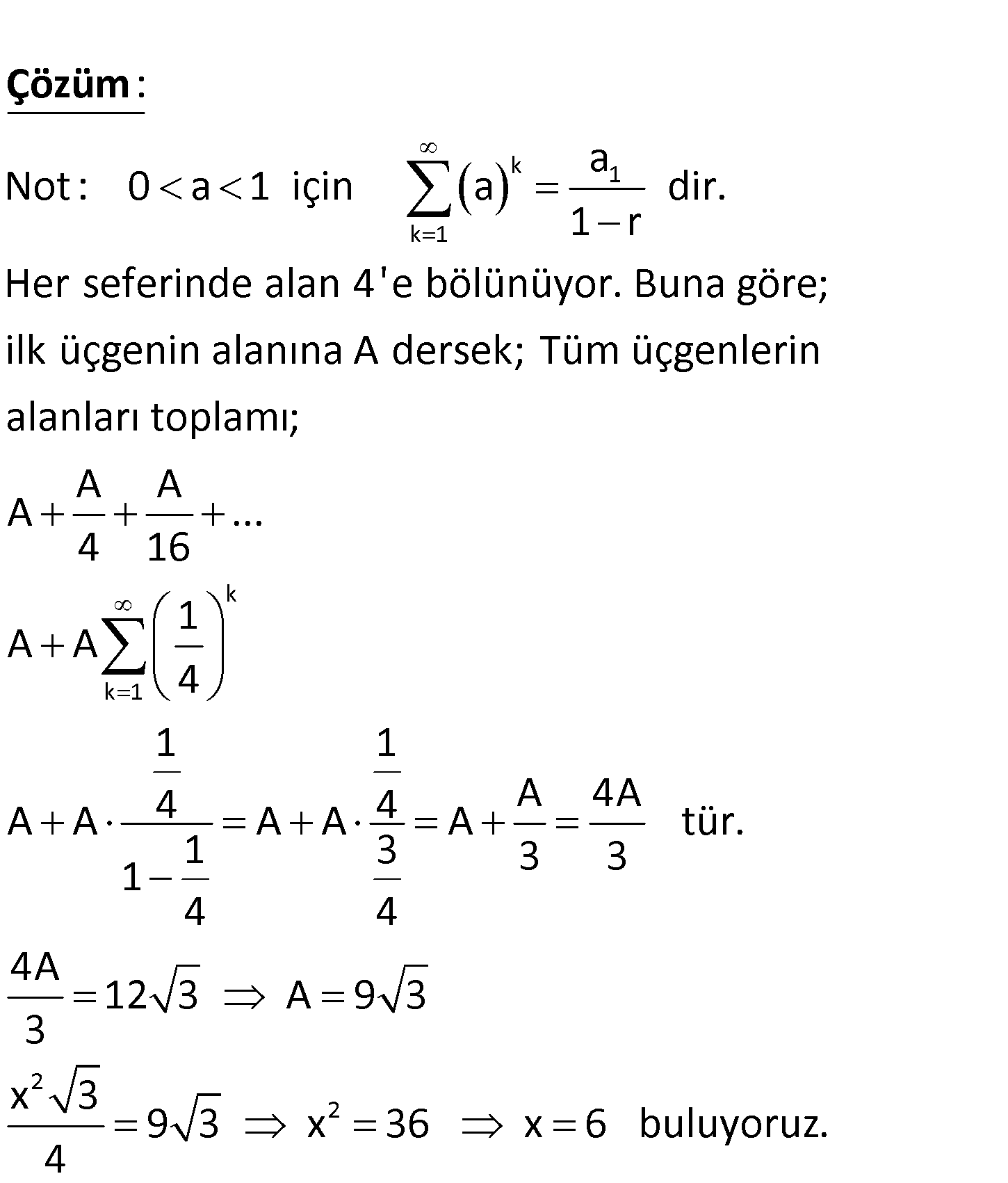
Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
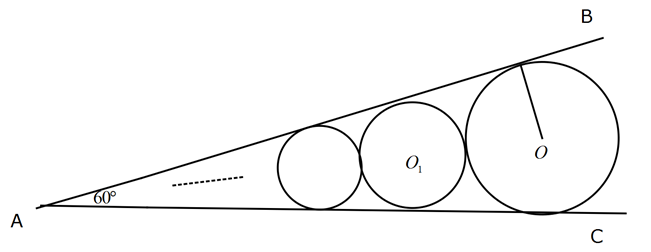
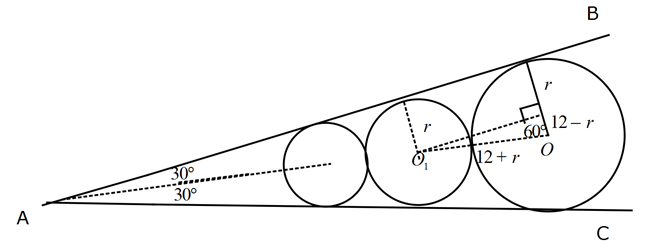
www.matematikkolay.net Şekilde m BAC 60 dir. Bu açının kollarına teğet ve r 12 cm olacak şekilde O merkezli çember çizili 1 2 – yor. Bu açının kollarına ve çembere teğet O mer – kezli çember çiziliyor. Bu işleme A noktası kadar devam ediliyor. Bu şekilde çizilerek oluşturulan çemberlerin alanları toplamı kaç cm dir? A) 96 B) 108 C) 162 D) 192 E) 206 www.matematikkolay.net 30 60 90 üçgeninden diğer çemberin yarıçapını bulabiliriz. 12 r 1 24 2r 12 r 12 r 2 : Çözüm 12 3r r 4 tür. En büyük çemberin yarıçarpı 12 cm iken, bir önceki çemberin yarıçapı 4 cm oluyor. 1 oranında küçülerek devam edeceği 3 k 2 2k 2 k k 0 k 0 k 0 k k 0 2 k k 0 anlaşılıyor. Buna göre alanlar toplamı : 1 1 r 12 144 3 3 1 1 9 144 144 144 162 9 1 8 1 9 cm bulunur. 1 Not : 0 r 1 için r dir. 1 r 11
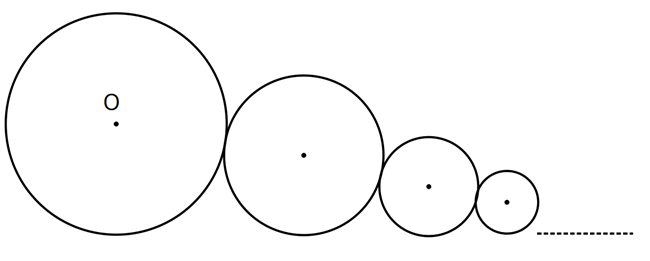
www.matematikkolay.net e Şekilde birbirine teğet sonsuz daire vardır. O merkezli dairenin yarıçapı 4 birim ve bundan sonra g 2 len her bir dairenin yarıçapı bir önceki – 3 nin yarıçapının ü kadar olduğuna göre, 4 bu dairelerin tümünün alanları toplamı kaç br dir? 128 256 64 A) B) C) 16 D) 8 E) 7 7 7 2 İlk dairenin alanı r 16 dir. Alanlar, yarıçapın karesi ile orantılıdır. 3 Alanların oranı 4 : Çözüm 2 2 k k k 0 k 0 9 dır. Buna göre; 16 9 İkinci dairenin alanı 16 dur. 16 9 Üçüncü dairenin alanı 16 dur. 16 … Bu alanların toplamı; 9 9 1 16 16 16 16 16 9 1 16 1 16 16 16 16 9 16 k k 0 256 buluruz. 7 7 1 Not : 0 a 1 için a 1:00 AM www.matematikkolay.net 27
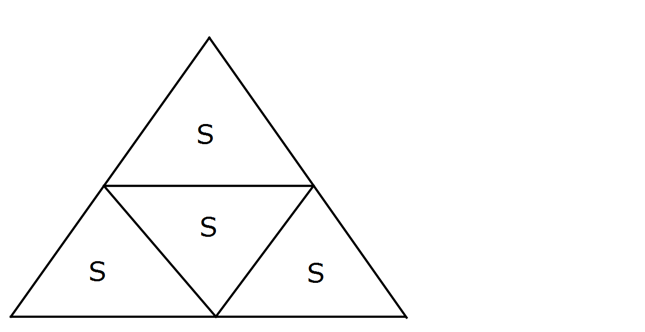
Kenar uzunluğu 4 br olan bir eşkenar üçgenin kenarlarının orta noktaları birleştirilerek yeni bir e 2 şkenar üçgen elde ediliyor. Bu işlem elde edilen üçgenlerin her birine uygulandığında bütün üçgenlerin alanları toplamı kaç br dir? 16 3 8 3 A) 16 3 B) 8 3 C) 6 3 D) E) 3 3 www.matematikkolay.net k 1 k 1 a Not : 0 a 1 için a dir. 1 r Her seferinde alan 4’e bölünüyor. Buna göre; ilk üç : Çözüm k k 1 2 genin alanına A dersek; Tüm üçgenlerin alanları toplamı; A A A … 4 16 1 A A 4 1 1 4 4 A 4A A A A A A tür. 1 3 3 3 1 4 4 4 3 A 4 3 olduğundan; 4 4A 4.4 3 16 3 buluruz. 3 3 3 38
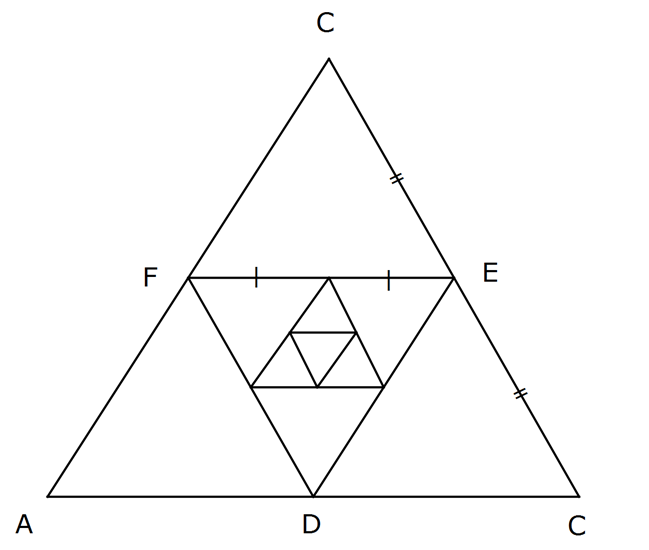
www.matematikkolay.net Şekilde bir kenarının uzunluğu x birim olan ABC eş – kenar üçgenin kenarlarının orta noktalarını köşe kabul eden DEF eşkenar üçgeni çiziliyor. Daha sonraki her bir eşkenar üçgen, bir öncekinin kenar uzunluklarının orta noktaları birleştirilerek elde ediliyor. Elde edilen eşkenar üçgenlerin alanları toplamı 12 3 birimkare olduğuna göre, x kaçtır? A) 2 B) 4 C) 6 D) 8 E) 12 www.matematikkolay.net k 1 k 1 a Not : 0 a 1 için a dir. 1 r Her seferinde alan 4’e bölünüyor. Buna göre; ilk üç : Çözüm k k 1 2 2 genin alanına A dersek; Tüm üçgenlerin alanları toplamı; A A A … 4 16 1 A A 4 1 1 4 4 A 4A A A A A A tür. 1 3 3 3 1 4 4 4A 12 3 A 9 3 3 x 3 9 3 x 36 x 6 buluyoruz. 4 51

