Soru Sor sayfası kullanılarak Diziler konusu altında İki sayı arasında dizi oluşturma ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU

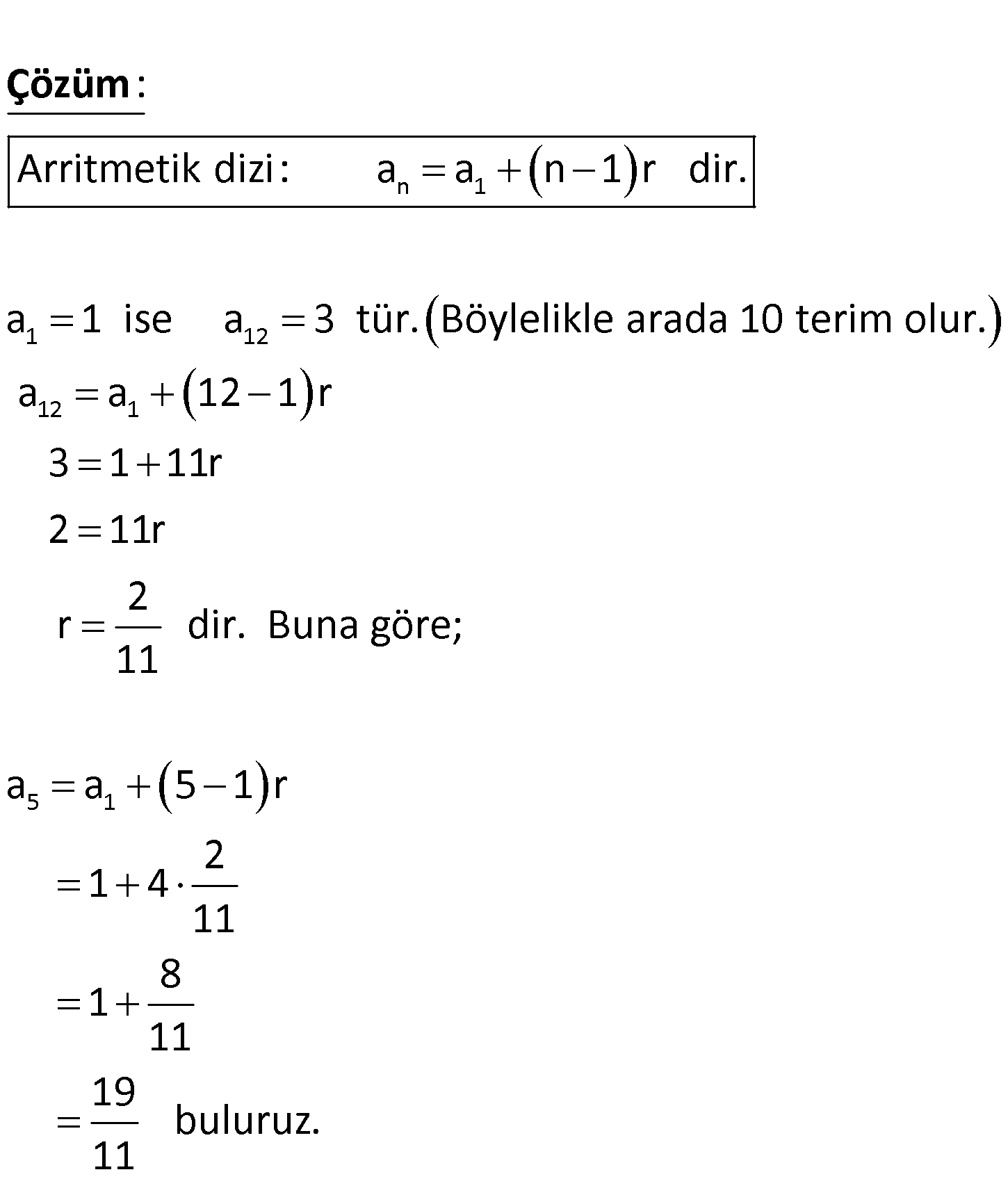
2.SORU


3.SORU


4.SORU


5.SORU


6.SORU


7.SORU

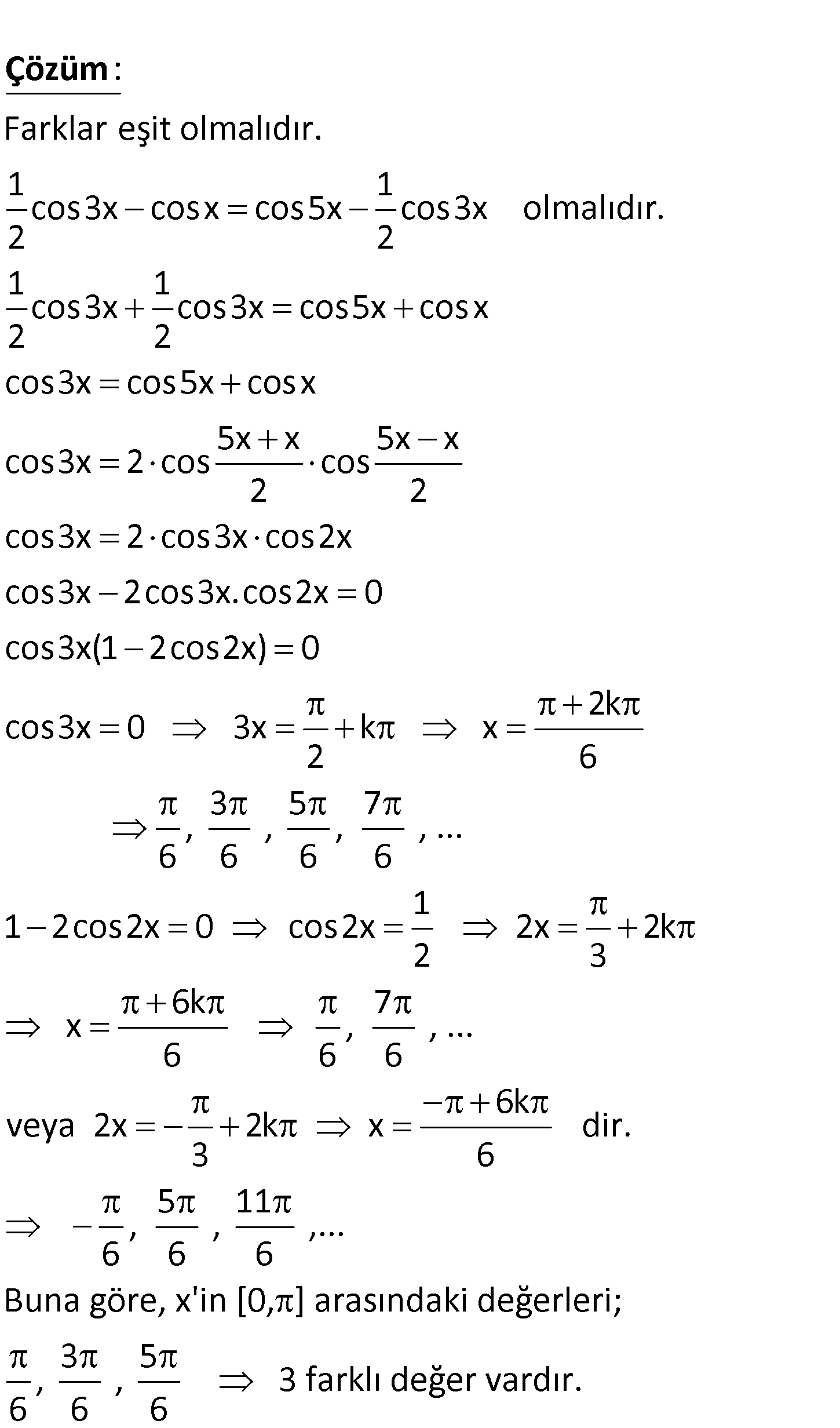
8.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
www.matematikkolay.net 1 ile 3 bir aritmetik dizinin iki terimidir. Bu iki terim arasında 10 terim daha bulunduğuna göre, beşinci terim kaçtır? 19 20 21 22 23 A) B) C) D) E) 11 11 11 11 11 n 1 1 12 Arritmetik dizi: a a n 1 r dir. a 1 ise a 3 tür. Böylelikle arada 10 teri : Çözüm 12 1 5 1 m olur. a a 12 1 r 3 1 11r 2 11r 2 r dir. Buna göre; 11 a a 5 1 r 2 1 4 11 8 1 11 19 buluruz. 11 64
a1 iki basamaklı bir doğal sayı olmak üzere, 11 ile a1 arasında aritmetik dizi oluşturacak şekilde a 2 tane terim yerleştirildiğinde ilk altı terimin toplamı kaç olur? A) 108 B) 144 C) 180 D) 216 E) 252 www.matematikkolay.net a1 ile 11 arasına a 2 tane terim yerleştirilince dizinin toplam terim sayısı a olur. Bu dizi : Çözüm nin ilk terimi 11 , Son terimi a1 ise a1 11 1 a olmalıdır. dir. r a1 11 a 1 r 10a 1 11 a 1 r 10a 10 a 1 r 10 a 1 a 1 r r 10 dur. İlk altı terim 11,21,31,41,51,61 61 11 72 Toplamları 6 2 2 6 3 216 buluruz. 69
3, a, b, c, 12 sonlu dizisi pozitif terimli bir geomet – rik dizi olduğuna göre, a.b.c çarpımı kaçtır? 2 2 3,a,b,c,12 geometrirk bir dizinin terimleri ise; b 3.12 a.c olmalı. b 36 b 6 (terimler po : Çözüm zitif olduğundan) a.c 36 dır. a.b.c 36.6 216 bulunur. 28
2 1 ile a arasına aritmetik dizi oluşturacak şekilde a tane terim yerleştiriliyor. Buna göre, oluşan bu dizinin ilk üç terim toplamı – nın eşiti aşağıdakilerden hangisidir? A) a B) 2a C) 3a D) 2a-1 E) 3a-2 www.matematikkolay.net 2 a tane 2 1 …. a a 2 sayıda terim var. Son terim 1 k.(a 1) a dir. : Çözüm 2 k(a 1) a 1 k. (a 1) (a1) (a1) k a 1 dir. İlk üç terim toplamı; 1 1 k 1 2k 3 3k 3 3.(a 1) 3 3a 3 3a buluruz . 13
1 2 3 n 6, a , a , a , …, a , 72 dizisi ortak farkı 6 olan bir aritmetik dizisidir. Buna göre, n kaçtır? A) 10 B) 11 C) 12 D) 13 E) 14 1 n n 1 9 a 6 6 12 dir. a 72 6 66 dır. a a (n 1)d 66 12 (n 1)6 54 (n 1)6 n 1 9 n 10 dur. : Çözüm www.matematikkolay.net 31
2, a, b, c, 24 bir aritmetik dizinin ardışık 5 terimi ise ab c kaçtır? Or tanca terim, kendisine eşit uzaklıktaki terimlerin ortalamasına eşittir. 2 24 b 13 tür. 2 a : b Çözüm c 13 ise a c 26 dır. 2 Buna göre; a b c 13 26 39 buluruz. 45
www.matematikkolay.net 1 cosx, cos3x, cos5x terimleri sırasıyla bir arit – 2 metik dizinin ardışık üç terimi olmasını sağl ayan x açısının 0, aralığında kaç değeri vardır? A) 2 B) 3 C) 4 D) 5 E) 6 www.matematikkolay.net Farklar eşit olmalıdır. 1 1 cos3x cosx cos5x cos3x olmalıdır. 2 2 1 1 cos3x cos3x cos5x cosx 2 2 cos : Çözüm 3x cos5x cosx 5x x 5x x cos3x 2 cos cos 2 2 cos3x 2 cos3x cos2x cos3x 2cos3x.cos2x 0 cos3x(1 2cos2x) 0 2k cos3x 0 3x k x 2 6 3 5 7 , , , , … 6 6 6 6 1 1 2cos2x 0 cos2x 2x 2k 2 3 6k 7 x , , … 6 6 6 6k veya 2x 2k x dir. 3 6 5 11 , , ,… 6 6 6 Buna göre, x’in [0, ] arasındaki değerleri; 3 5 , , 3 farklı değer vardır. 6 6 6 22
n n n 2 3 5 n 1 3 4 5 x y olmak üzere, a ve b aritmetik dizileri • a x, a , a , y, a , … • b b , x, b , b , b , y, b 7 3 2 5 4 … biçiminde tanımlanıyor. a a Buna göre, oranı aşağıdakilerden hangi – b b sine eşittir? 2 3 3 4 5 A) B) C) D) E) 3 4 2 3 4 www.matematikkolay.net n a dizisinin ilk terimi x, 4.terimi y ise; y x artış miktarını olarak yazabiliriz. 3 : Çözüm n 3 2 5 4 b dizisinin 2. terimi x, 6.terimi y ise; y x artış miktarını olarak yazabiliriz. 4 Buna göre; y x a a tek artış b b tek artış 3 y x 4 buluruz. 3 430

