Soru Sor sayfası kullanılarak Diziler konusu altında Dizinin terimleri arasındaki bir denklemden istenen terimi bulma ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU

3.SORU


4.SORU

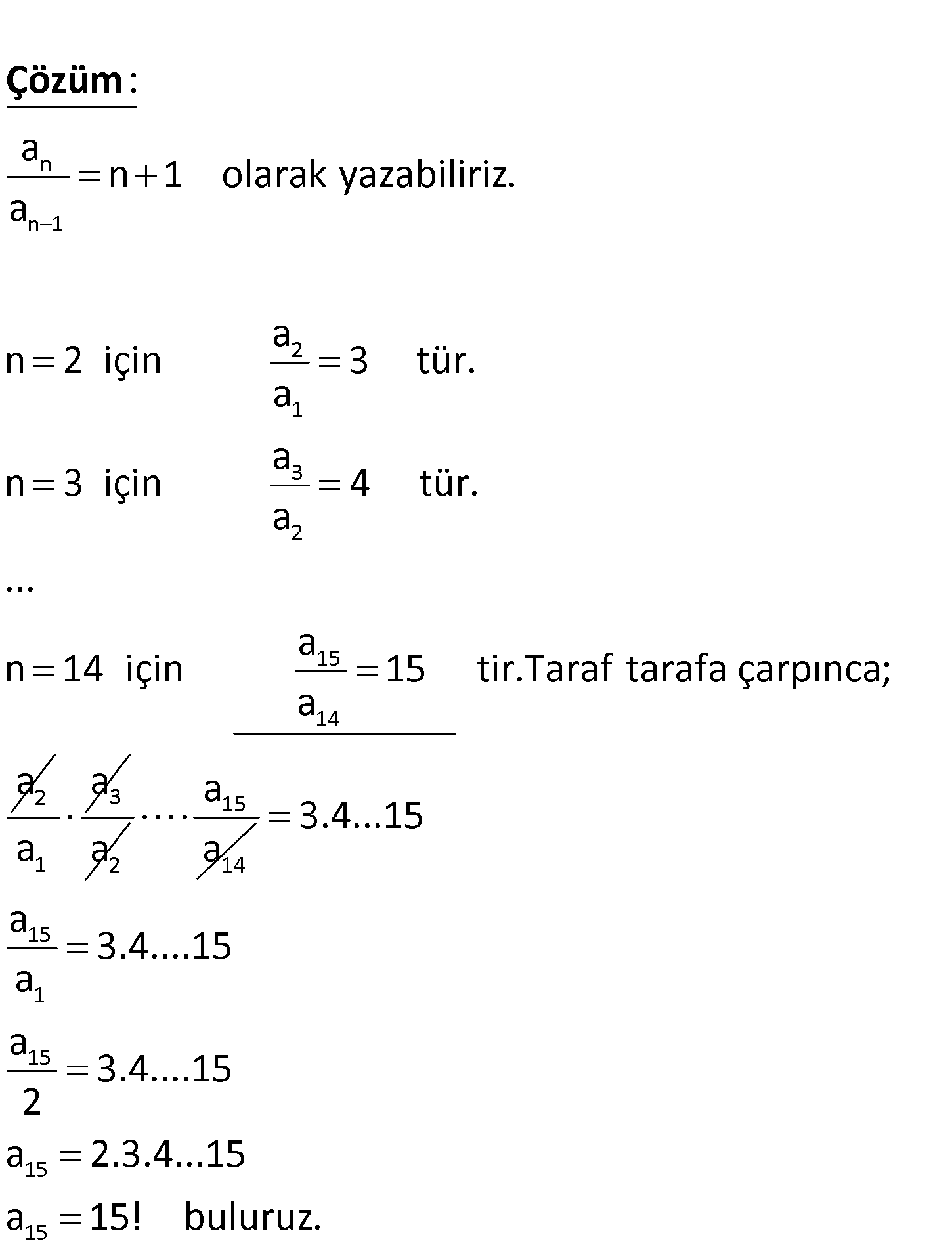
5.SORU


6.SORU


7.SORU
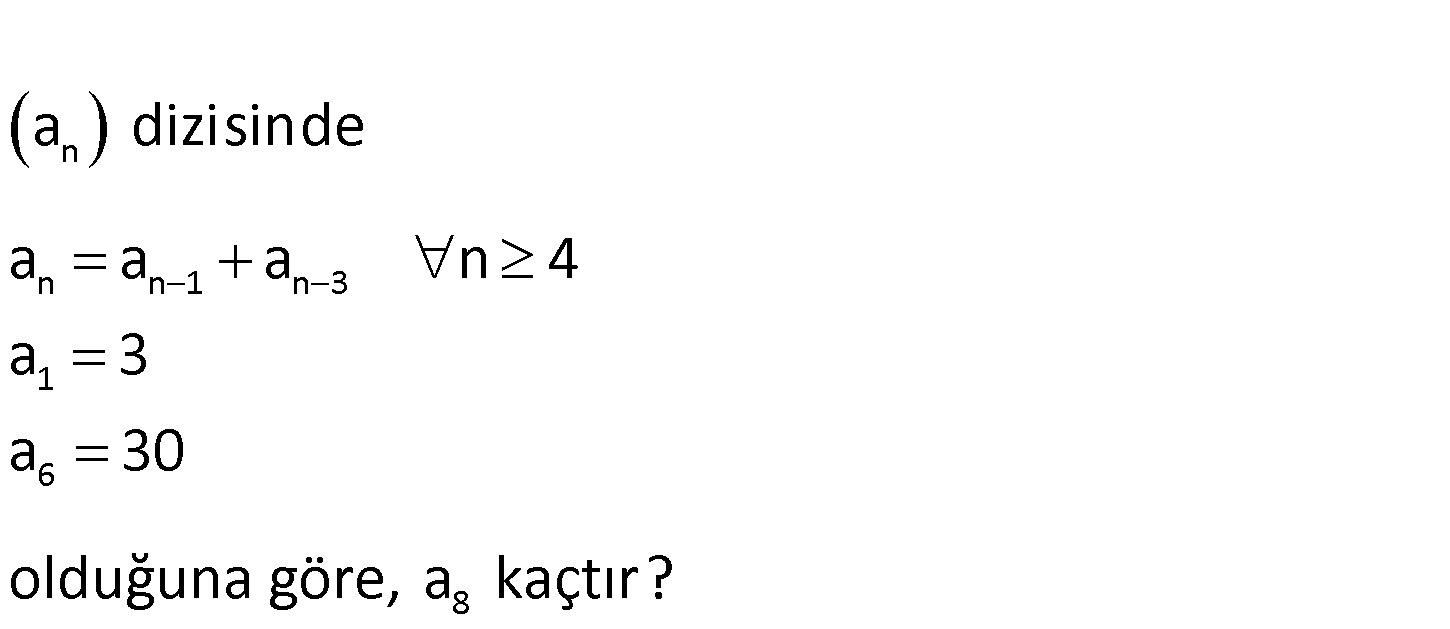
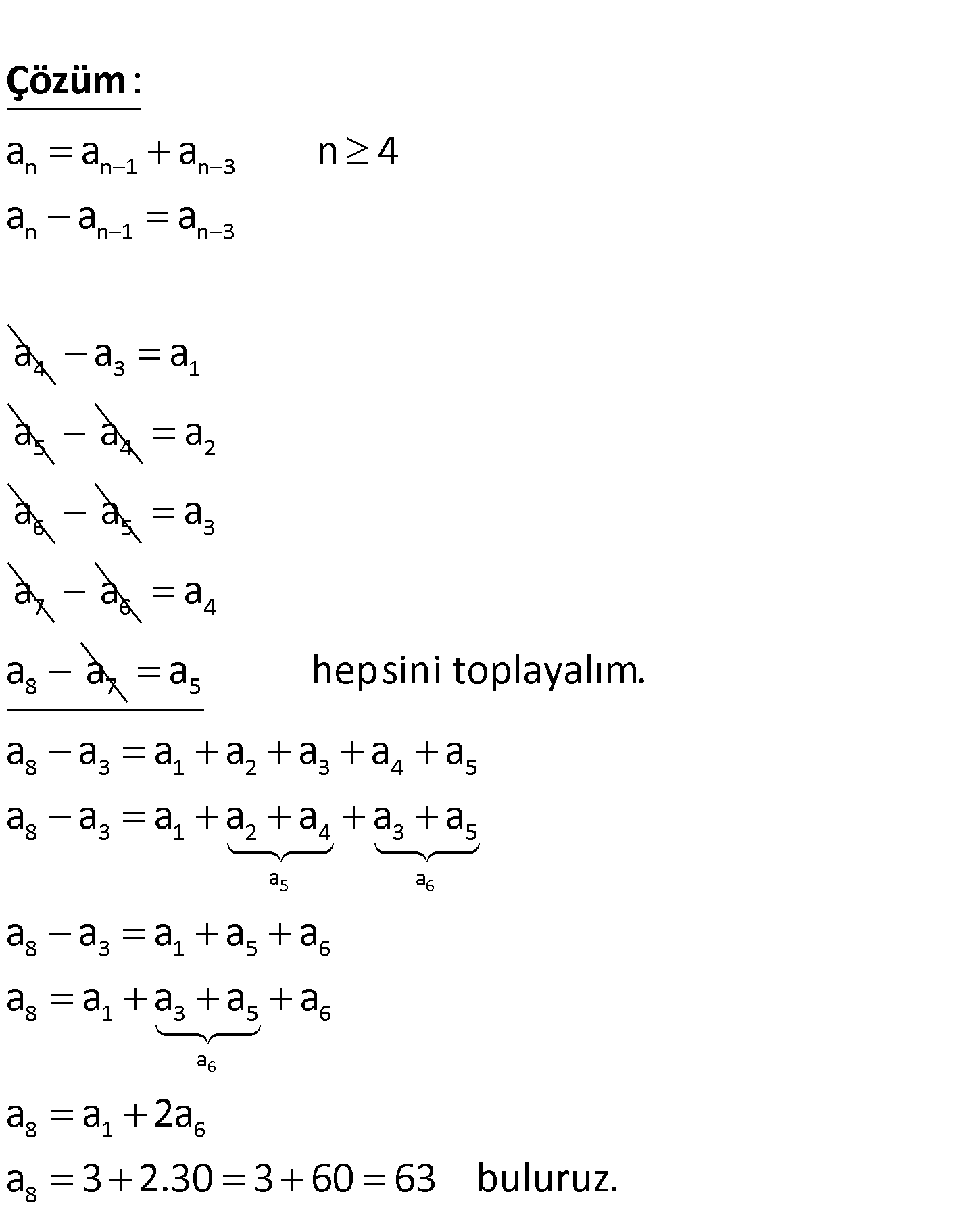
8.SORU

9.SORU
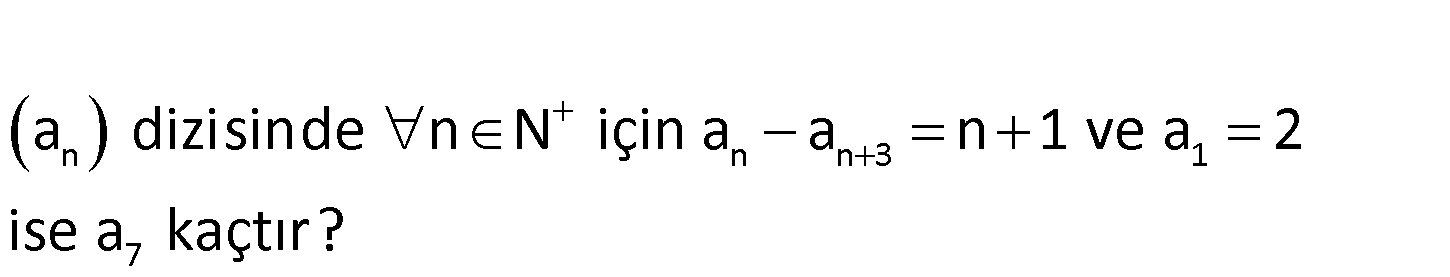
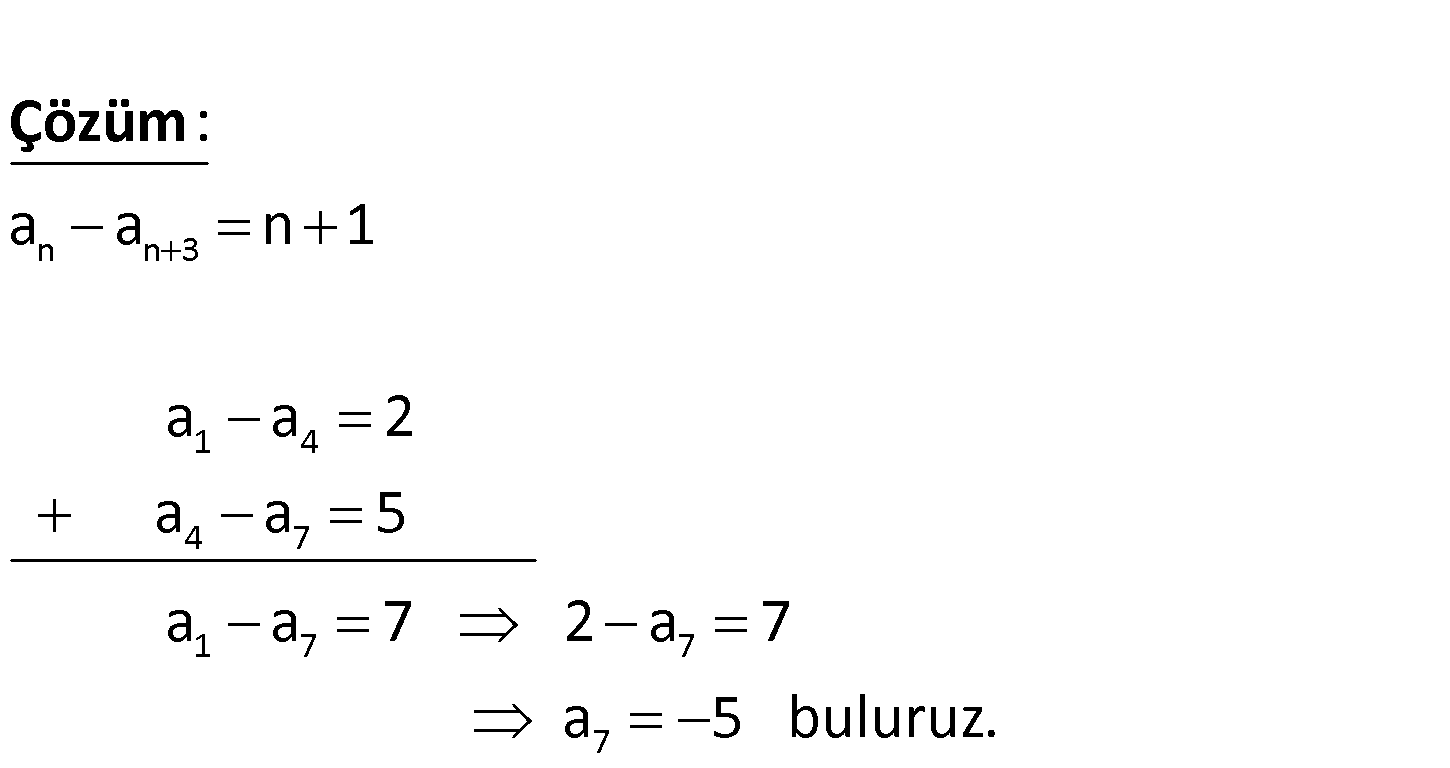
10.SORU

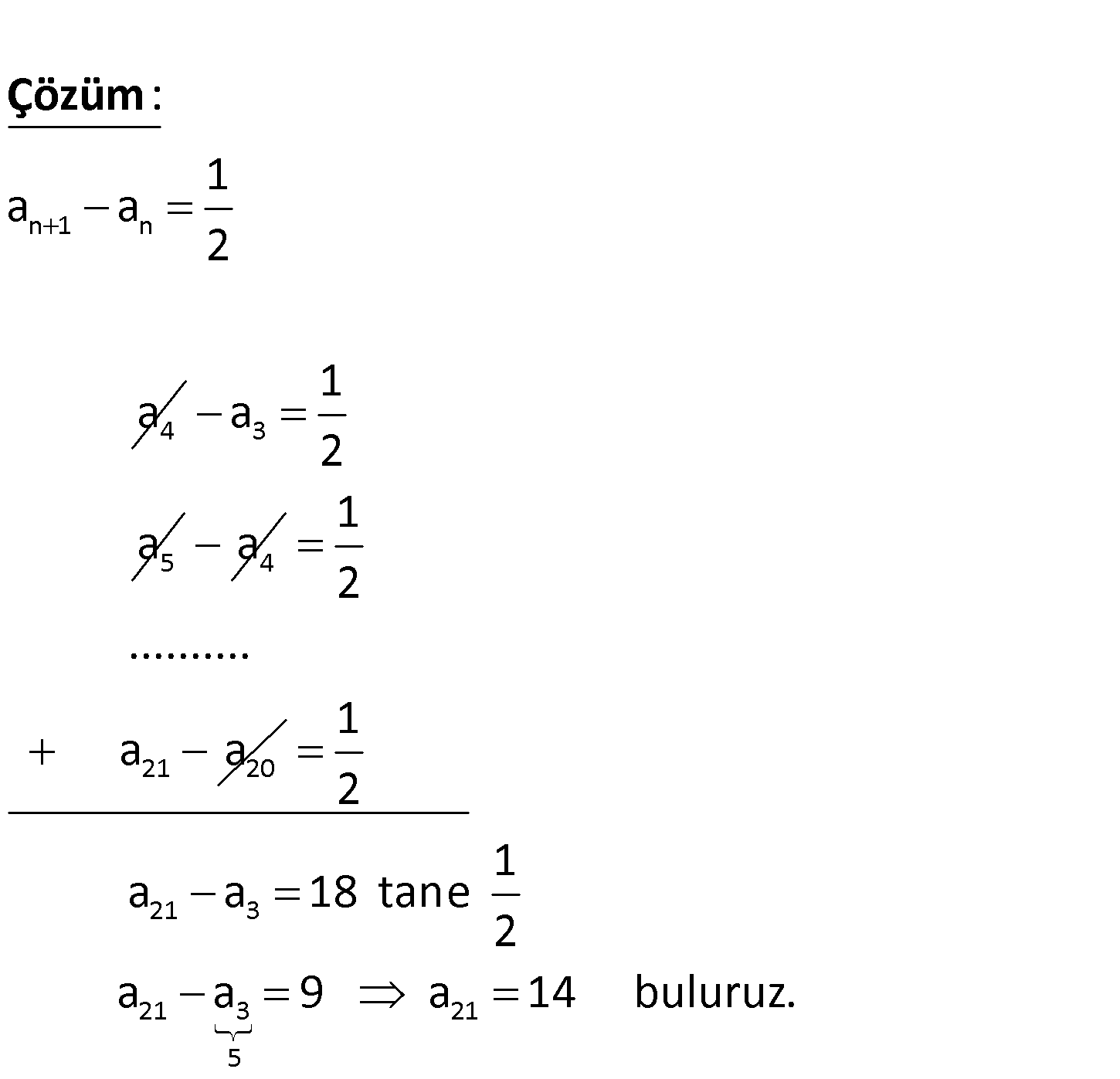
11.SORU


12.SORU

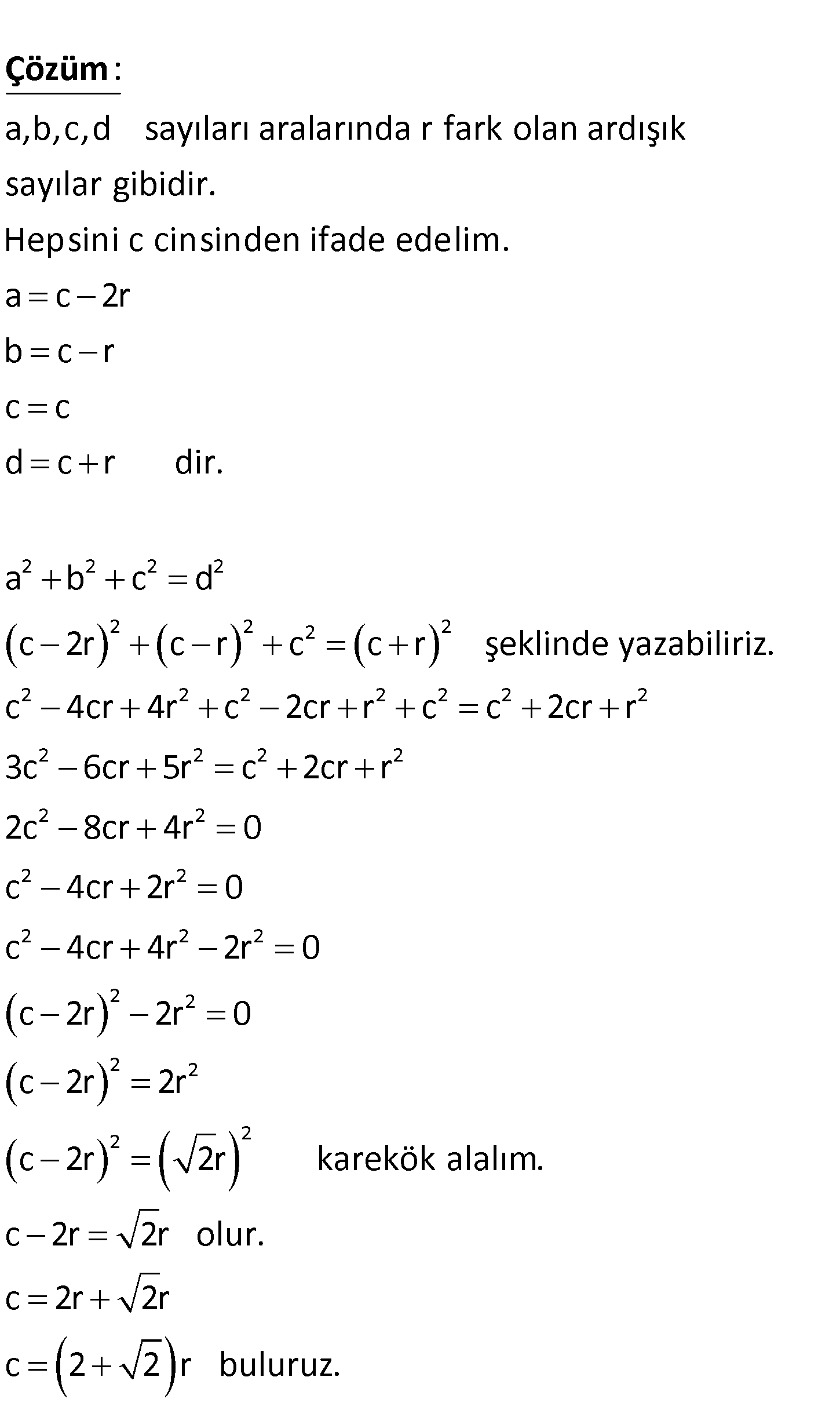
13.SORU


14.SORU

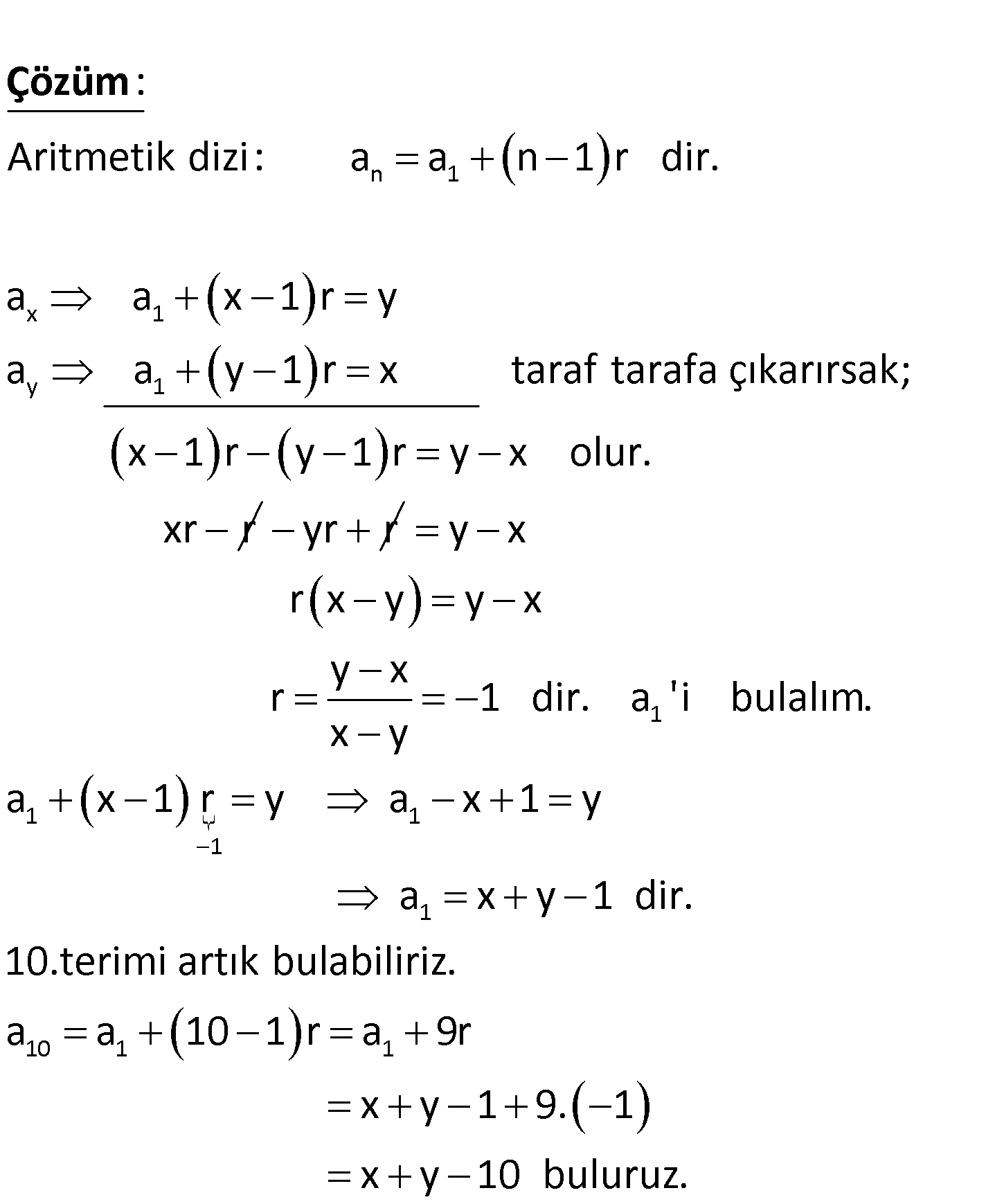
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
n n 1 1 n 30 a a n ve a 28 koşullarını sağlayan a dizisi için a kaçtır? A) 407 B) 400 C) 396 D )352 E)340 www.matematikkolay.net n n 1 1 2 a a n şeklinde yazabiliriz. n 1 için a a : Çözüm 2 1 n 2 için a 3 a 3 2 n 3 için a 4 a 29 3 …. n 29 için a 30 1 30 1 30 30 30 a 29 dur. taraf tarafa toplayınca a a 1 2 … 29 olur. 29.30 a a 2 28 a 435 a 4 30 7 a407 buluruz. 71
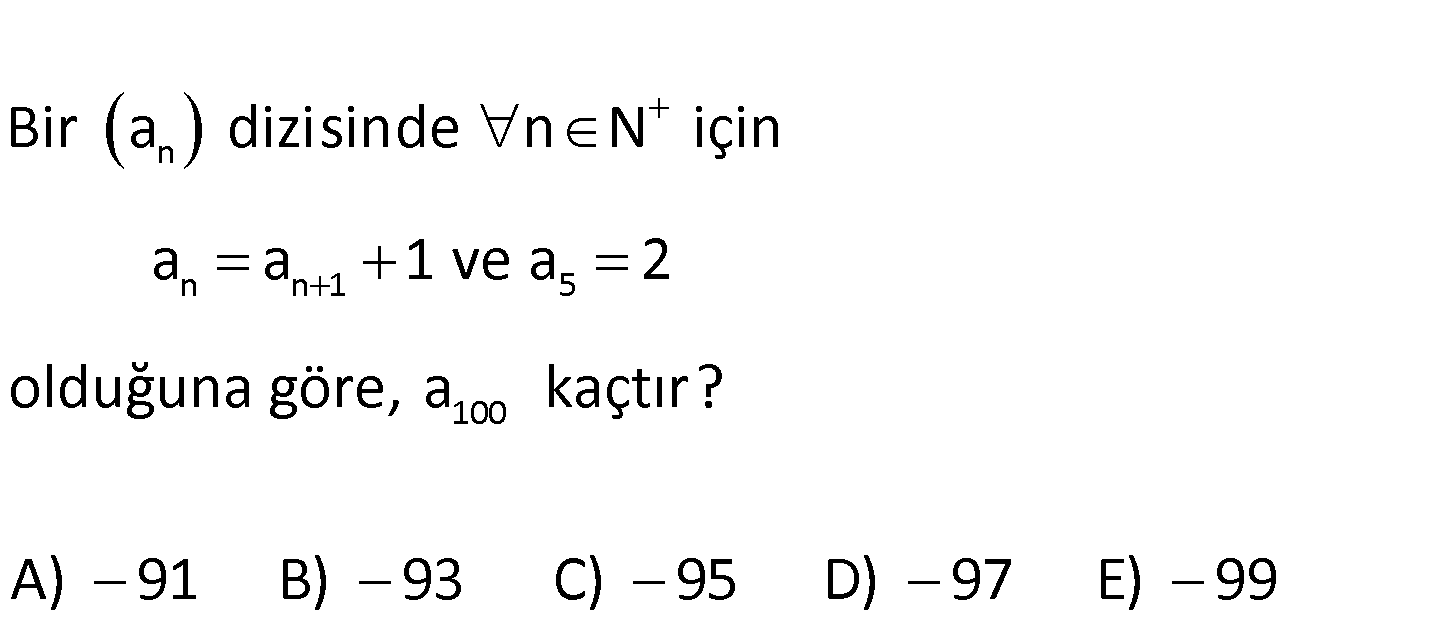
n n n 1 5 100 Bir a dizisinde n N için a a 1 ve a 2 olduğuna göre, a kaçtır? A) 91 B) 93 C) 95 D)97 E)99 www.matematikkolay.net n n 1 5 6 a a 1 olarak yazabiliriz. n 5 için a a : Çözüm 6 1 dir. n 6 için a 7 a 99 1 dir. … n 99 için a 100 5 100 99 5 Terim sayısı 1 95 1 5 100 100 a 1 dir. taraf tarafa toplayınca a a 1 1 … 1 a a 95 2 a 95 100 100 a 93 a 93 buluruz. 73
n n 1 n 1 20 Bir a dizisinde n N için a 2 a ve a 3 olduğuna göre, a değeri kaçtır? A) 39 B) 40 C) 41 D) 42 E) 43 www.matematikkolay.net n 1 n 2 a a 2 olarak yazabiliriz. n 1 için a : Çözüm 1 3 a 2 dir. n 2 için a 2 a 20 19 2 dir. … n 19 için a a 20 1 19 1 Terim sayısı 1 19 1 20 1 20 2 dir. taraf tarafa toplayınca a a 2 2 … 2 a a 2.19 a 3 38 20 a 41 buluruz. 74
n 1 n n 1 15 Genel terimi a olan dizide a 2 ve her n 2 için a n 1 .a olduğuna göre, a kaçtır? A) 14! B) 15! C) 16! D) 17! E) 18! www.matematikkolay.net n n 1 2 1 3 a n 1 olarak yazabiliriz. a a n 2 için 3 tür. a a n 3 için a : Çözüm 2 15 14 2 4 tür. … a n 14 için 15 tir.Taraf tarafa çarpınca; a a 3 1 a a 2:00 AM 15 14 a a 15 1 15 15 15 3.4…15 a 3.4….15 a a 3.4….15 2 a 2.3.4…15 a 15! buluruz.75
n 3 1 2 4 6 a pozitif terimli bir geometrik dizidir. a 9.a a a 90 olduğuna göre, a aşağıdaki 4 5 6 7 8 lerden hangisidir? A) 3 B) 3 C) 3 D) 3 E) 3 www.matematikkolay.net n 1 n 1 3 1 3 1 2 3 1 Geometrik dizi: a a r şeklinde gösterilir. Buna göre; a a .r a a .r : Çözüm 2 3 1 2 4 3 1 1 3 1 1 1 1 1 1 5 5 6 6 1 dir. a 9.a ise r 9 r 3 tür. r 3 olamaz. Pozitif terimli bir diziymiş. a a 90 ise a .r a .r 90 a .3 a .3 90 a .3 a .27 90 30.a 90 a 3 tür. a a .r 3.3 3 buluruz. 84
n 2 5 1 3 7 a pozitif terimli bir geometrik dizidir. a 8 a a .a 1 olduğuna göre, a aşağıdaki lerden hangisidir? 1 1 1 1 1 A) B) C) D) E) 128 64 32 16 8 www.matematikkolay.net n 1 n 1 2 1 5 Geometrik dizi: a a r şeklinde gösterilir. Buna göre; a a 8 ise a : Çözüm 1 .r a 4 3 1 3 2 1 1 2 1 2 1 1 6 6 1 1 1 8 8 r dir. .r r 2 a .a 1 ise a .a r 1 a .r 1 1 a 1 2 a 2 dir. 2 olamaz. Dizi pozitif terimliymiş. 1 1 1 a .r 2 2 buluruz. 2 64 32 85
n n n 1 n 3 1 6 8 ? a dizisinde a a a n 4 a 3 a 3 0 ol u d ğuna göre, a kaç r t ı www.matematikkolay.net n n 1 n 3 n n 1 n 3 4 a a a n 4 a a : a a Çözüm 3 1 5 a a a 4 a 2 6 a a5 a 3 7 a a6 a 4 8 7 a a a 5 6 6 5 8 3 1 2 3 4 5 8 3 1 2 4 3 5 a a 8 3 1 5 6 8 1 3 5 6 a 8 1 6 8 a hepsini toplayalım. a a a a a a a a a a a a a a a a a a a a a a a a a a 2a a 3 2.30 3 60 63 buluruz. 26
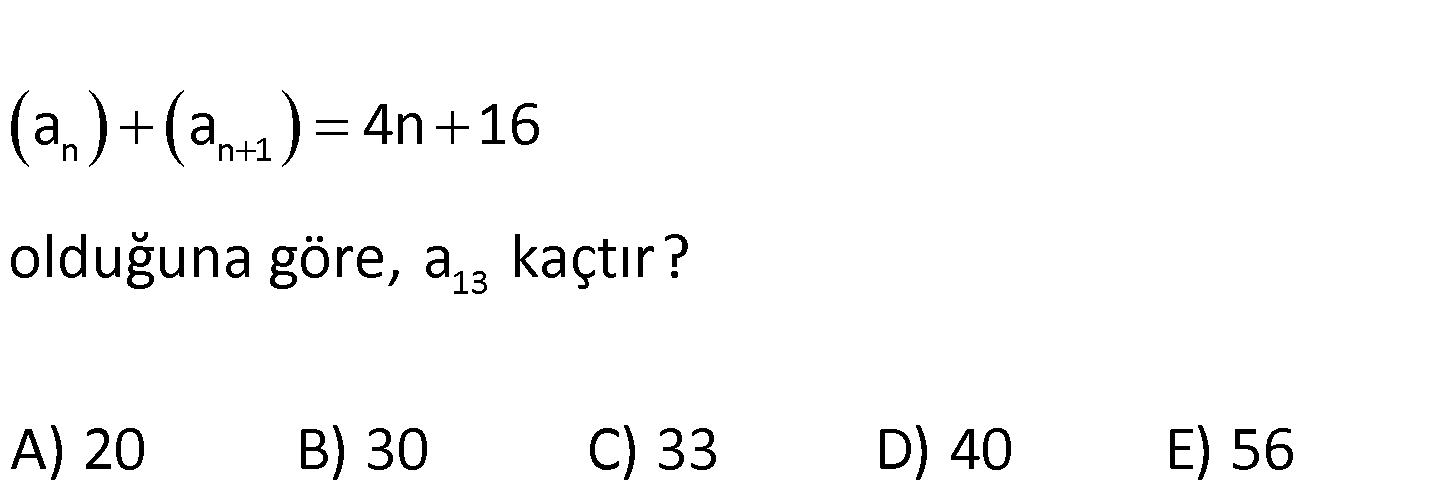
n n 1 13 a a 4n 16 olduğuna göre, a kaçtır? A) 20 B) 30 C) 33 D) 40 E) 56 n n 1 n 1 n 1 1 n n 1 1 1 n : a a 4n 16 a a n 1 r olsun. a a n.r olur. a a a .r r a n.r 4n 16 2.n.r Çözüm 1 1 1 1 13 1 2a r 4n 16 2r 4 r 2 dir. 2a r 16 2a 2 16 a 9 dur. a a 13 1 .r 9 12 .2 9 24 33 buluruz. 35
www.matematikkolay.net n n n 3 1 7 a dizisinde n N için a a n 1 ve a 2 ise a kaçtır? n n 3 1 4 4 7 1 7 7 a a n 1 a a 2 a a 5 a a 7 2 a 7 : Çözüm a75 buluruz. 44
n n 1 n 3 21 a dizisinde, 1 a a ve a 5 olduğuna göre, 2 a kaçtır? A) 9 B) 11 C) 12 D) 14 E) 15 n 1 n 4 1 a a 2 a : Çözüm 3 5 1 a 2 a a4 21 20 1 2 ………. a a 21 3 21 3 21 5 1 2 1 a a 18 tane 2 a a 9 a 14 buluruz. www.matematikkolay.net 47
n n n 1 a aritmetik dizisinde a 2 a eşitliği veriliyor. Bu dizinin ilk 10 terimin toplamı 115 olduğuna göre, dizinin ilk terimi kaçtır? 3 5 A) B) 2 C) D) 3 E) 4 2 2 www.matematikkolay.net n n 1 a a 2 dir. Bu dizinin ilk terimi a olsun. İlk 10 terim toplamı; a a 2 a 4 … a 18 10a (2 : Çözüm Terim sayısı x Ortalama 4 .. 18) 115 10a 10.10 115 10a 100 115 10a 15 3 a buluruz. 2 52
www.matematikkolay.net a, b, c, d pozitif terimli ortak farkı r olan bir aritme – tik dizinin ilk dört terimidir. 2 2 2 2 a b c d olduğuna göre, c’nin r cinsinden değeri nedir? A) 2 2 r B) 1 2 r C) 2r D) 1 2r E) 1 2r www.matematikkolay.net a,b,c,d sayıları aralarında r fark olan ardışık sayılar gibidir. Hepsini c cinsinden ifade Çözüm: 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 edelim. a c 2r b c r c c d c r dir. a b c d c 2r c r c c r şeklinde yazabiliriz. c 4cr 4r c 2cr r c c 2cr r 3c 6cr 5r c 2cr r 2c 8cr 4r 0 c 4cr 2r 0 c 4cr 4r 2r 0 c 2r 2r 0 c 2 2 2 2 2 r 2r c 2r 2r karekök alalım. c 2r 2r olur. c 2r 2r c 2 2 r buluruz. 61
www.matematikkolay.net 5 İlk terimi ortak farkına eşit olan bir aritmetik dizi – nin, ilk 15 terimin çarpımı 8 .15! dir. Buna göre, dizinin yirmi beşinci terimi kaçtır? A) 25 B) 50 C) 75 D) 100 E) 125 Ortak fark r olsun. İlk terim r ise; 2.terim 2r 3.terim 3r … şeklinde ilerler. İlk 15 t :Çözüm 5 5 5 15 tane erimin çarpımı 8 .15! ise; r.2r.3r.4r…15r 8 .15! dir. 1.2.3.4…15.r.r.r.r..r 8 .15! 15! .r15 85.15! 15 5 15 5 15 3 5 15 15 r 8 r 8 r 2 r 2 r 2 dir. 25.terim 25r 25.2 50 buluruz. 62
www.matematikkolay.net x y Bir aritmetik dizide, a y ve a x olduğuna göre, dizinin onuncu terimi aşağıdaki – lerden hangisidir? A) x y B) x y 10 C) x y D) x 10y E) x 10y n 1 x 1 y 1 Aritmetik dizi: a a n 1 r dir. a a x 1 r y a a y 1 r x taraf taraf : Çözüm a çıkarırsak; x 1 r y 1 r y x olur. xr r yr r 1 1 1 1 1 y x r x y y x y x r 1 dir. a ‘i bulalım. x y a x 1 r y a x 1 y a x y 1 dir. 10.terimi artık bul 10 1 1 abiliriz. a a 10 1 r a 9r x y 1 9. 1 x y 10 buluruz. 63

