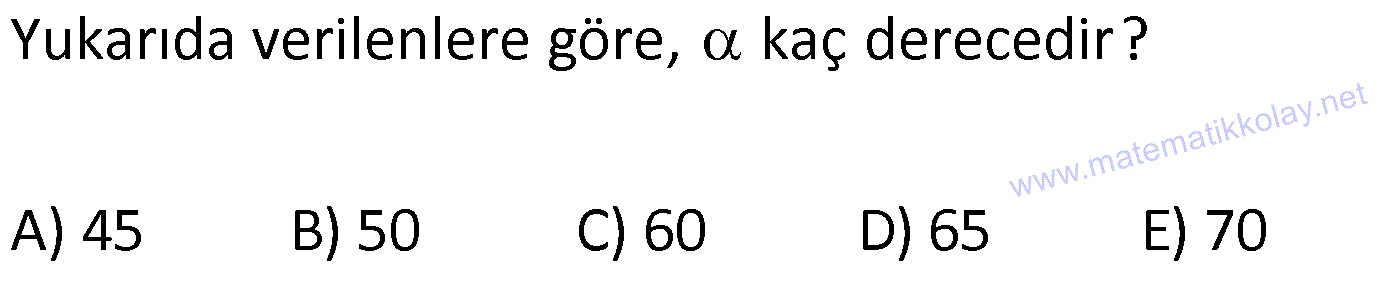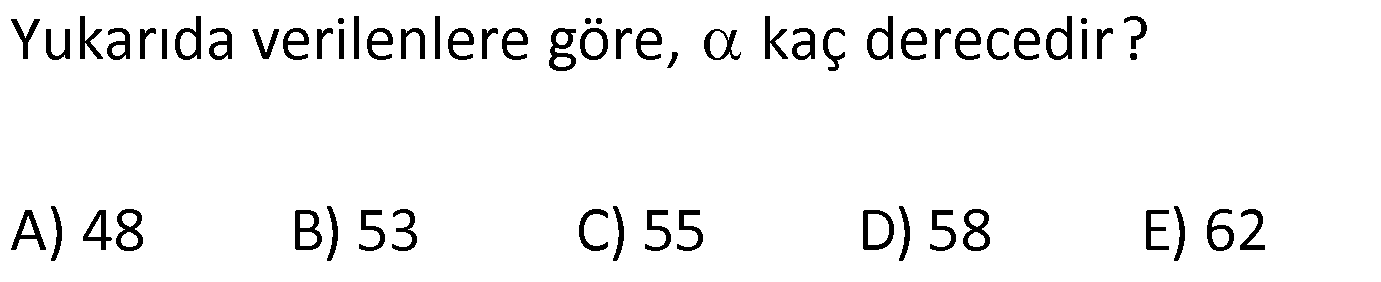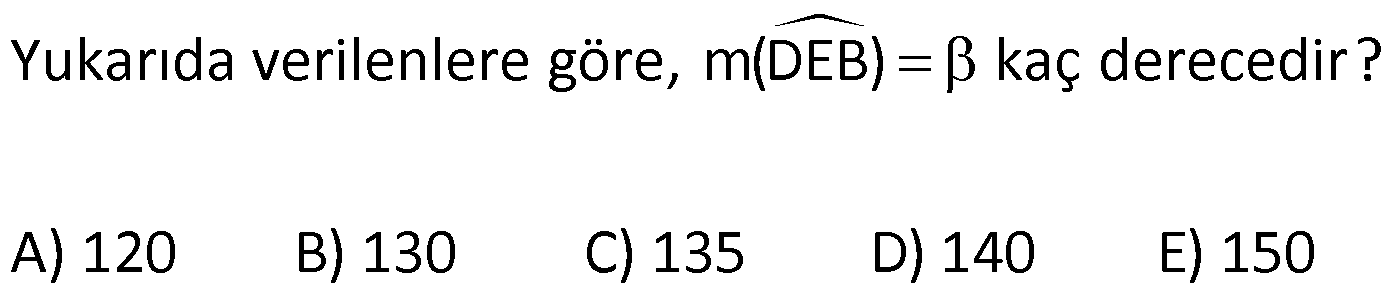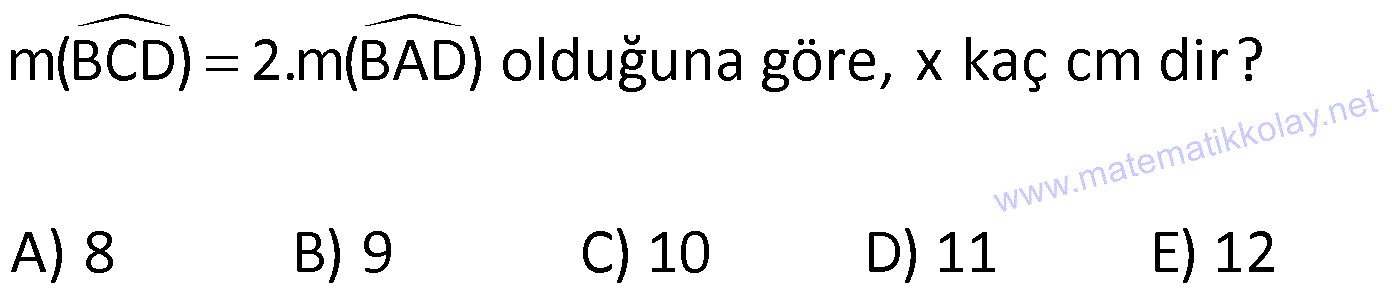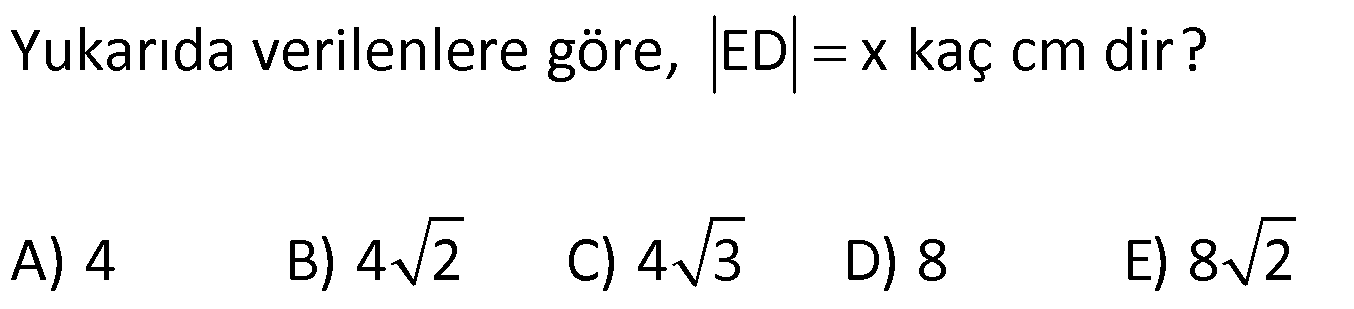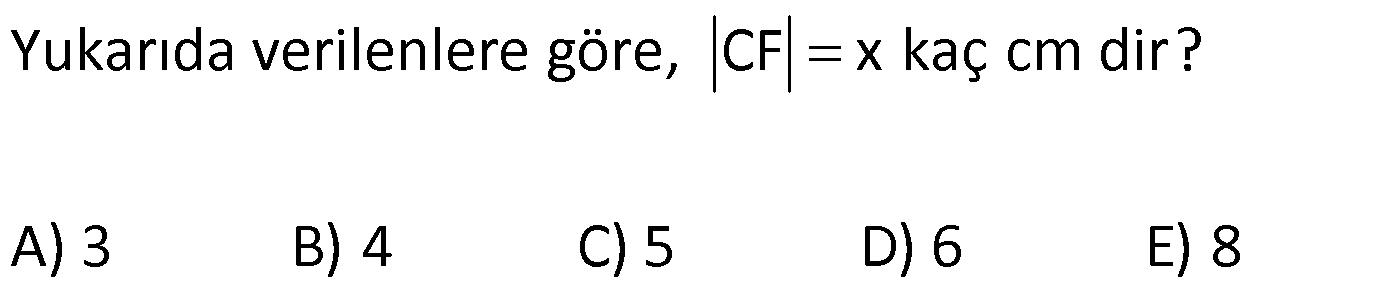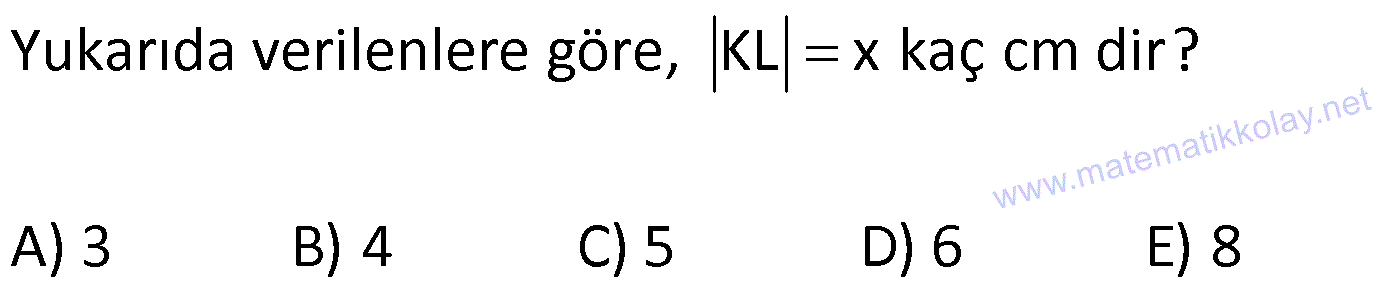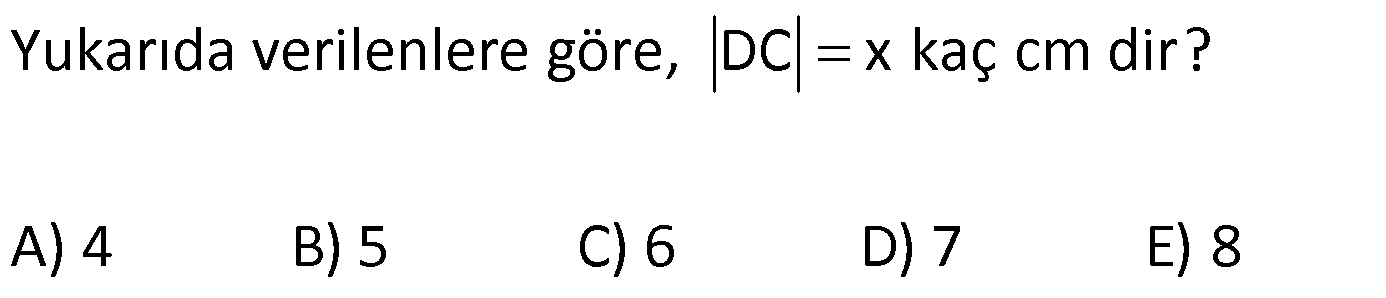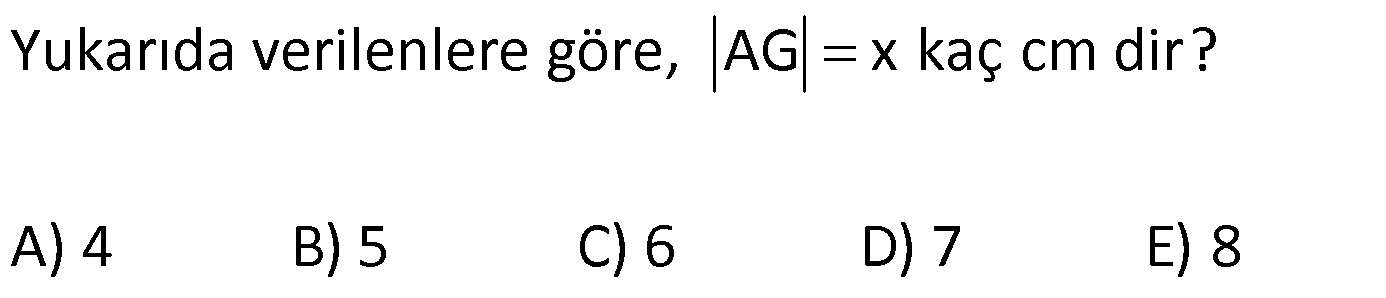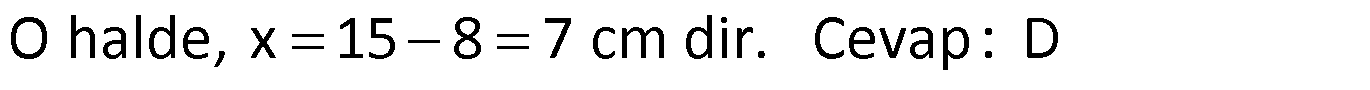Bu bölümde Yamukta Açı ve Uzunluk ile ilgili 18 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
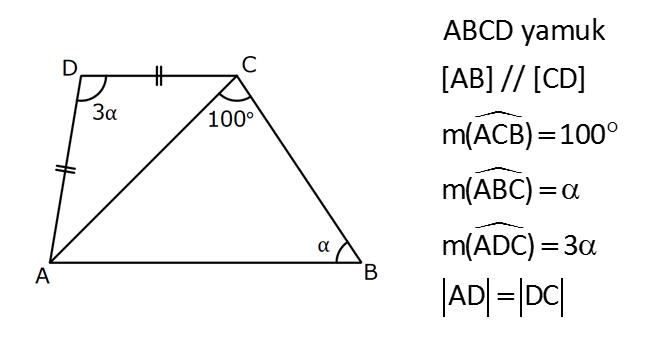
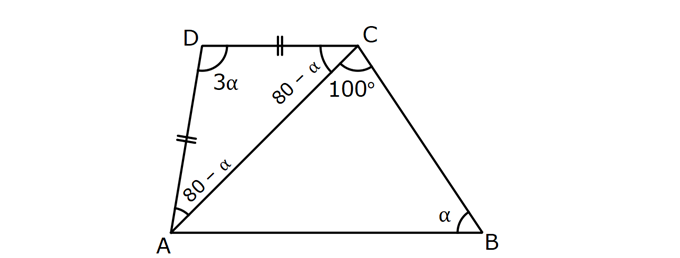
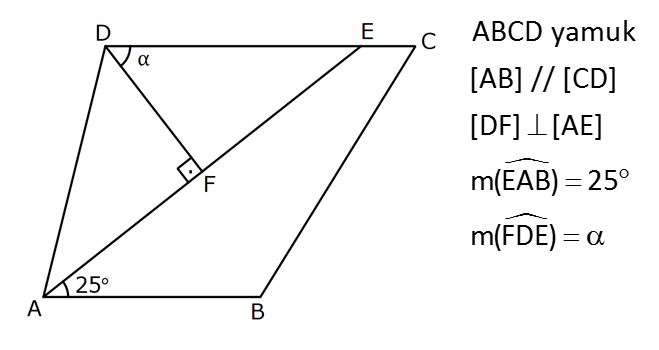
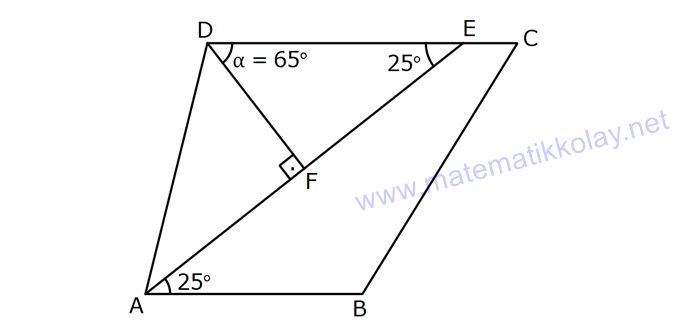
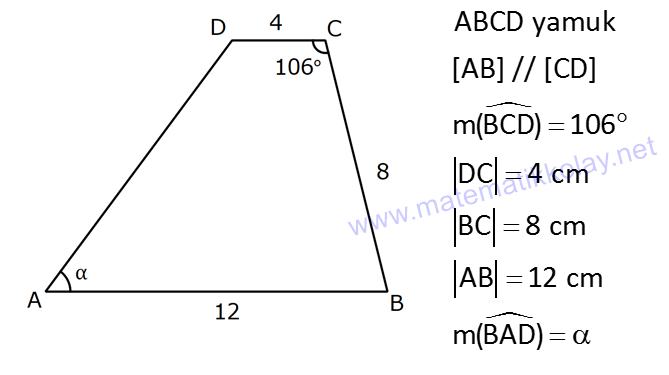
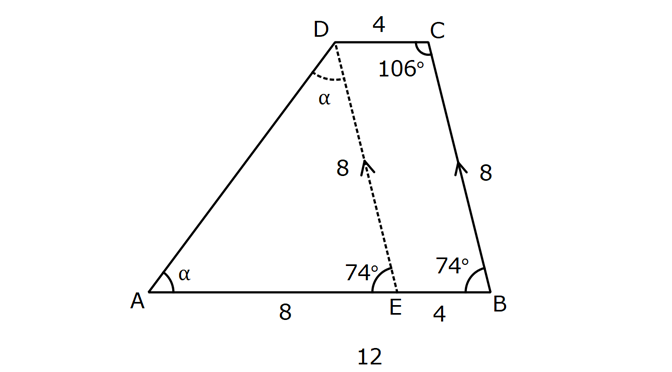
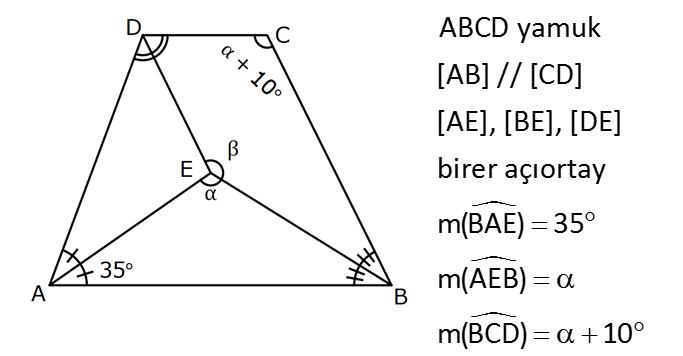
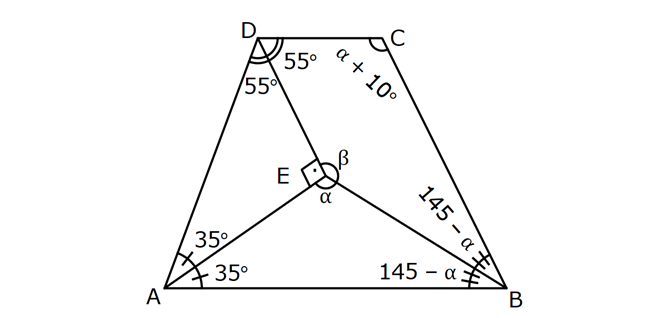
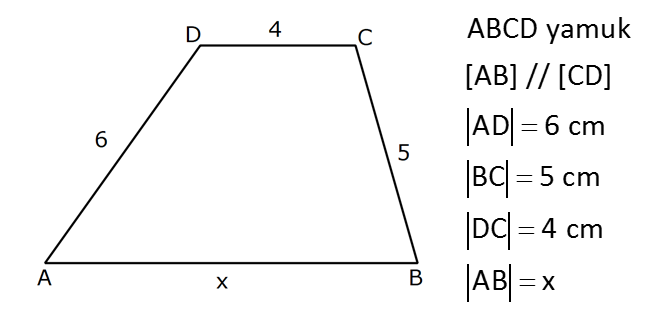
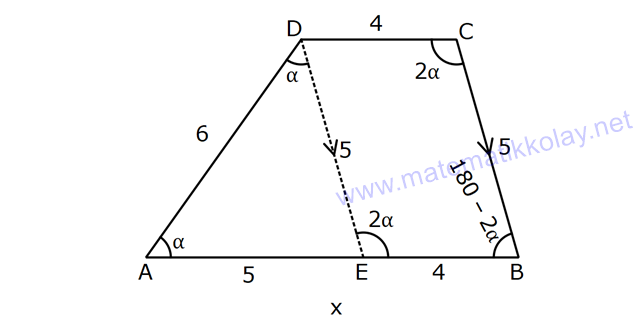
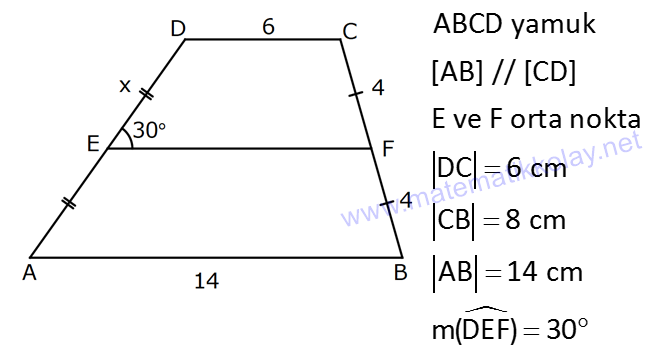
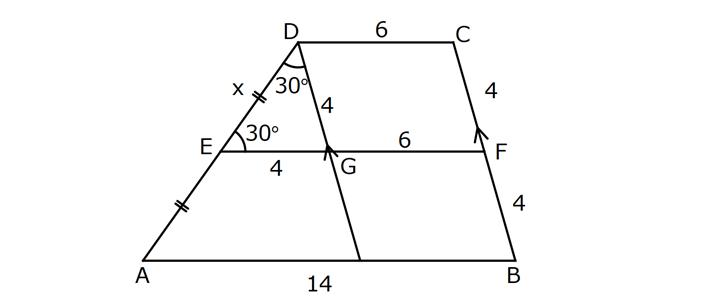
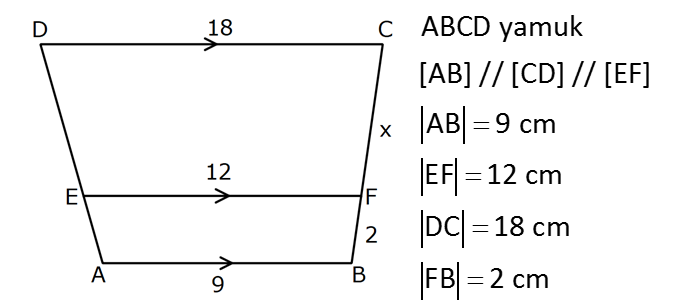
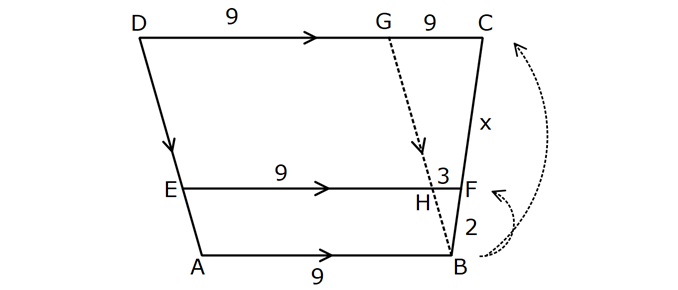
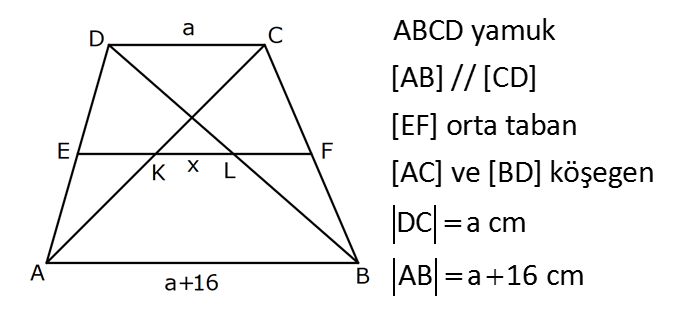
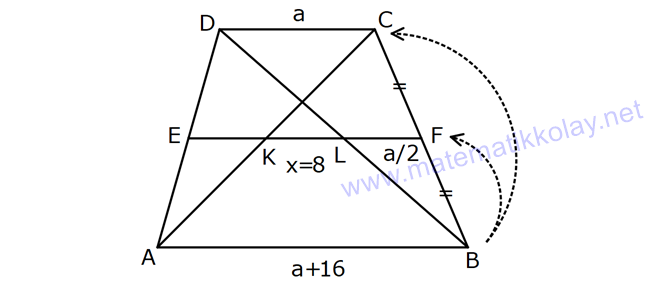
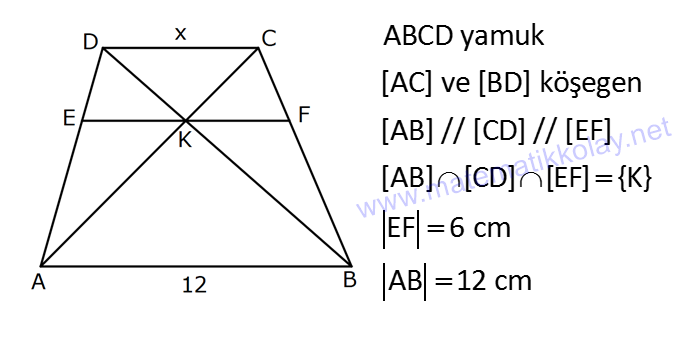
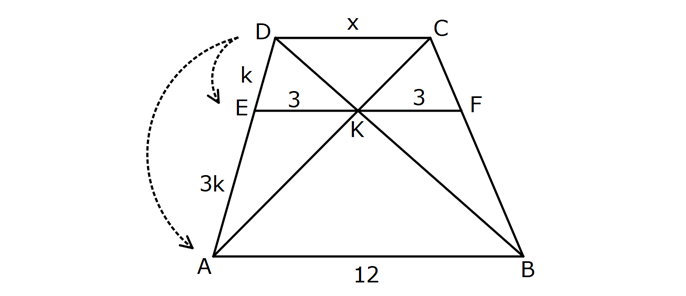
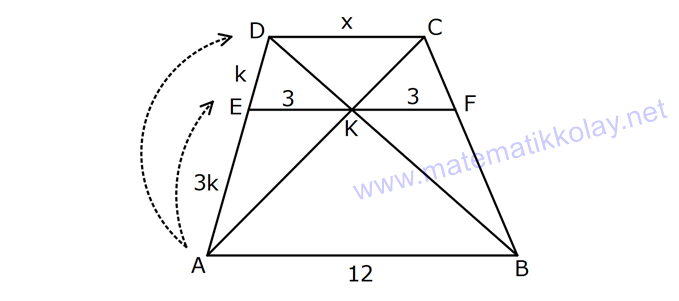
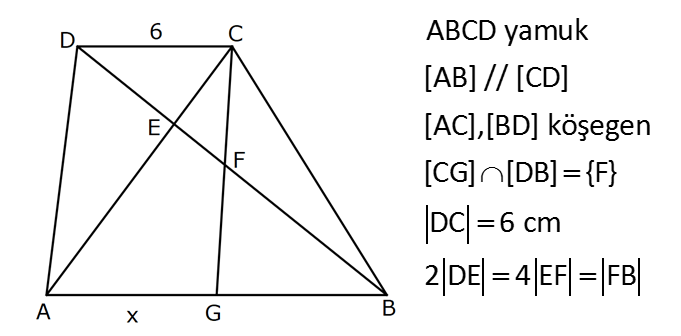
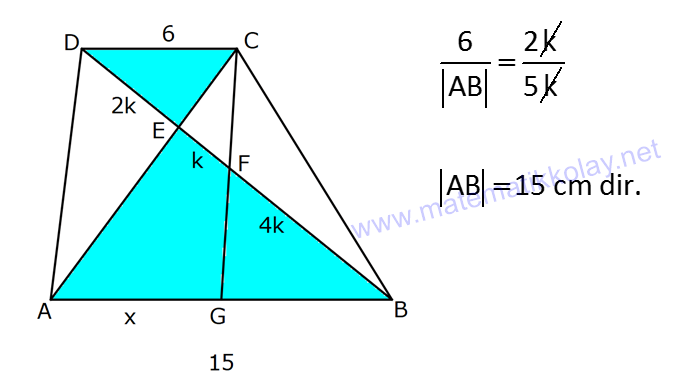
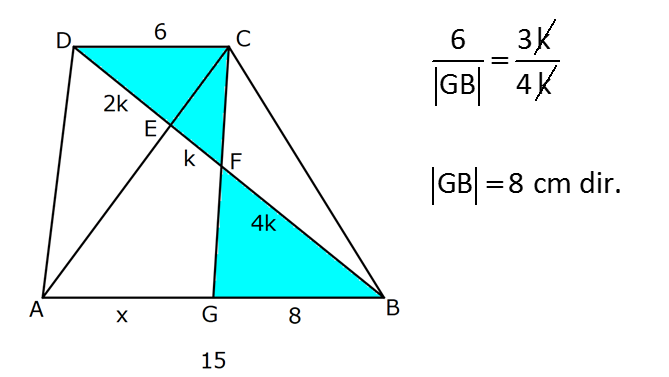
YAMUKTA AÇI – UZUNLUK www.matematikkolay.net 1) ABCD yamuk [AB] // [CD] m(ACB) 100 m(ABC) m(ADC) 3 AD DC Yukarıda verilenlere göre, kaç derecedir ? A) 20 B) 25 C) 35 D) 40 E) 50 ÇÖZÜM: Karşılıklı iki kenarı paralel olan dörtgenlere denir. ( [AB] // [CD] ) Paralel olan kenarlar, alt ve üst taban olarak isimlendirilir. Paralel olmayan kenarlara ise yan kenarlar denir. Bir yan ke Not : yamuk narın, tabanlarla oluşturduğu açıların toplamı 180 dir. (A+C=180 , B+D=180 ) Buna göre, m(ACD) 100 180 olmalıdır. m(ACD) 80 olur. ADC üçgeni ikizkenar üçgen olduğundan, 80 80 3 180 olmalı dır. 160 180 20 buluruz. Cevap : A 2) ABCD yamuk [AB] // [CD] [DF] [AE] m(EAB) 25 m(FDE) Yukarıda verilenlere göre, kaç derecedir ? A) 45 B) 50 C) 60 D) 65 E) 70 ÇÖZÜM: [AB] // [DC] olduğundan, m(DEA) 25 dir (İç ters açı) DFE üçgeninin iç açıları toplamından 25 90 180 65 buluruz. Cevap : D 3) ABCD yamuk [AB] // [CD] m(BCD) 106 DC 4 cm BC 8 cm AB 12 cm m(BAD) Yukarıda verilenlere göre, kaç derecedir ? A) 48 B) 53 C) 55 D) 58 E) 62 ÇÖZÜM: www.matematikkolay.net m(ABC) 180 106 74 dir. [BC] ye paralel olarak [DE] yi çizelim. EB 4 cm, DE 8 cm olur. AE 12 4 8 cm kalır. O halde, AED üçgeni ikizkenar bir üçgen olur. [DE] // [CB] olduğundan m(AED) 74 dir (Yöndeş Açı ). AED üçgeninin iç açıları toplamından 74 180 2 106 53 buluruz. Cevap: B 4) ABCD yamuk [AB] // [CD] [AE], [BE], [DE] birer açıortay m(BAE) 35 m(AEB) m(BCD) 10 Yukarıda verilenlere göre, m(DEB) kaç derecedir? A) 120 B) 130 C) 135 D) 140 E) 150 ÇÖZÜM: m(BAD) 35 35 70 dir. m(ADC) 180 70 110 olur. [DE] açıortayından dolayı m(EDC) 55 olur. EAB üçgeninin iç açıları toplamından, m(EBA) 35 180 m(EBA) 145 dır. [BE] açıortayından dolayı m(EBC) 145 dır . BCDE dörtgeninin iç açıları toplamından, 55 10 145 360 210 360 150 dir. Cevap : E 5) ABCD yamuk [AB] // [CD] AD 6 cm BC 5 cm DC 4 cm AB x m(BCD) 2.m(BAD) olduğuna göre, x kaç cm dir? A) 8 B) 9 C) 10 D) 11 E) 12 ÇÖZÜM: www.matematikkolay.net [BC] ye paralel olarak [DE] yi çizelim. DE 5 cm ve EB 4 cm olur. m(DAB) dersek, m(BCD) 2 olur. [AB] // [DC] olduğundan, m(ABC) 180 2 dır. [ED] // [BC] olduğundan, m(BEC) 2 dır. ADE üçgeninin iki iç aç ısının toplamı, diğer köşedeki dış açıya eşit olmalıdır. Yani m(ADE) 2 m(ADE) dır. O halde, ADE üçgeni ikizkenar bir üçgendir. AE 5 cm olur. x 5 4 9 cm buluruz. Cevap : B 6) ABCD yamuk [AB] // [CD] E ve F orta nokta DC 6 cm CB 8 cm AB 14 cm m(DEF) 30 Yukarıda verilenlere göre, ED x kaç cm dir ? A) 4 B) 4 2 C) 4 3 D) 8 E) 8 2 ÇÖZÜM: [EF] orta tabandır. 6 14 20 EF 10 cm dir. 2 2 D’den [BC] ye paralel çizelim. DG 4 cm, GF 6 cm olur. EG 4 cm kalır. O halde, DEG üçgeni bir 30 – 30 -120 üçgenidir. x 4 3 cm buluruz. Cevap : C Bir yam Not : ukta yan kenarların orta noktasını birleştiren doğru parçasına denir. Orta taban, alt ve üst tabana paraleldir ve uzunluğu alt ve üst taban uzunluklarının ortalamasıdır. orta taban 7) ABCD yamuk [AB] // [CD] // [EF] AB 9 cm EF 12 cm DC 18 cm FB 2 cm Yukarıda verilenlere göre, CF x kaç cm dir ? A) 3 B) 4 C) 5 D) 6 E) 8 ÇÖZÜM: www.matematikkolay.net [AD] ye paralel olarak [BG] yi çizelim. EH 9 cm olur. HF 3 cm kalır. BG 9 cm olur. GC 9 cm kalır. BHF üçgeni ile BGC üçgeni arasında benzerlik uygulayabiliriz. 3 9 3 2 2 x 6 x 4 cm buluruz. 2 x Cevap : B 8) ABCD yamuk [AB] // [CD] [EF] orta taban [AC] ve [BD] köşegen DC a cm AB a 16 cm Yukarıda verilenlere göre, KL x kaç cm dir ? A) 3 B) 4 C) 5 D) 6 E) 8 ÇÖZÜM: [LF], BDC üçgeninin orta tabanıdır. a LF cm olur. Ayrıca 2 [KF], ABC üçgeninin orta tabanıdır. a 16 a KF 8 cm olur. 2 2 O halde, x 8 cm kalır. Cevap : E Orta tabanda Not : köşegenlerin arasında kalan uzunluk üst ve alt taban arasındaki farkın yarısıdır. AB DC KL dir. 2 9) ABCD yamuk [AC] ve [BD] köşegen [AB] // [CD] // [EF] [AB] [CD] [EF] {K} EF 6 cm AB 12 cm Yukarıda verilenlere göre, DC x kaç cm dir ? A) 4 B) 5 C) 6 D) 7 E) 8 ÇÖZÜM: EK KF 3 cm dir. [EK] // [AB] olduğu için, DE 3 DA 12 4 DE k olsun, DA 4k olur. EA 3k kalır. www.matematikkolay.net 4 [EK] // [DC] olduğu için, 3k 3 x=4 cm buluruz. 4k x Paraleller arasındaki uzunluğu formül yardı- mıyla bulabiliriz. 1 1 1 dir. EK DC AB 1 1 1 3 x 12 4 1 1 3 12 12 x 2.Yol: 12 4 1 x 4 cm buluruz. x Cevap: A 10) ABCD yamuk [AB] // [CD] [AC],[BD] köşegen [CG] [DB] {F} DC 6 cm 2 DE 4 EF FB Yukarıda verilenlere göre, AG x kaç cm dir ? A) 4 B) 5 C) 6 D) 7 E) 8 ÇÖZÜM: 2k k 4k 2 DE 4 EF FB şeklinde yazalım. [AB] // [DC] olduğu için, Kelebek benzerliklerini yaparız. 6 2 k AB 5 k AB 15 cm dir. 6 3k GB 4 k GB 8 cm dir. O halde, x 15 8 7 cm dir. Cevap: D
