Bu bölümde Yamuğun Alanı ile ilgili 20 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
1.SORU
 |  |  |  |  |
Çözüm için Tıklayınız.
2.SORU
| | | | | |
Çözüm için Tıklayınız.
3.SORU
| | | | | |
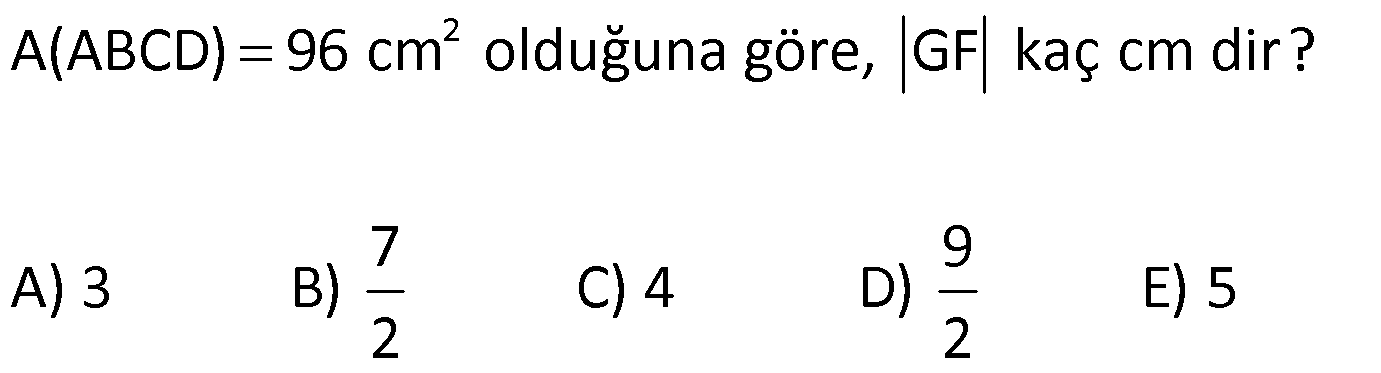
Çözüm için Tıklayınız.
4.SORU
| | | | | |
Çözüm için Tıklayınız.
5.SORU
| | | | | |
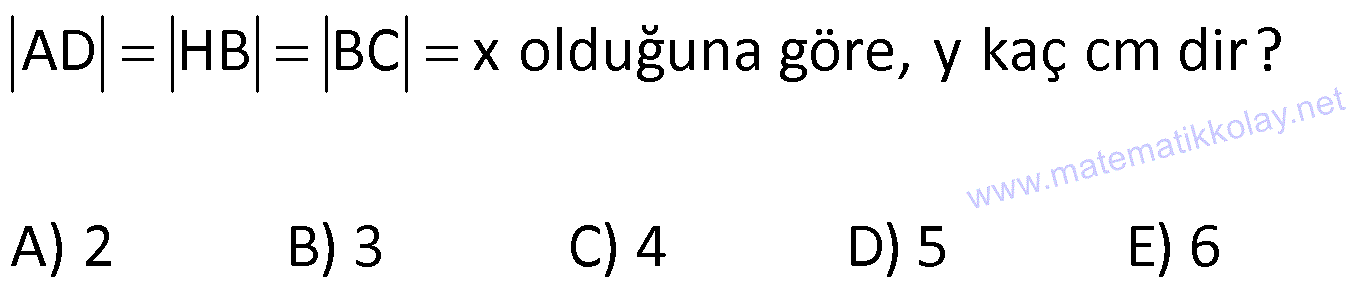
Çözüm için Tıklayınız.
6.SORU
| | | | | |
Çözüm için Tıklayınız.
7.SORU
| | | | | |
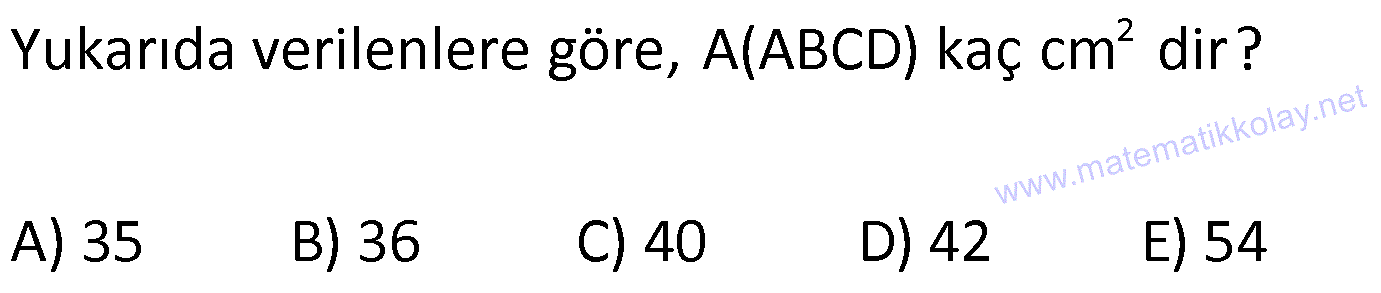
Çözüm için Tıklayınız.
8.SORU
| | | | | |
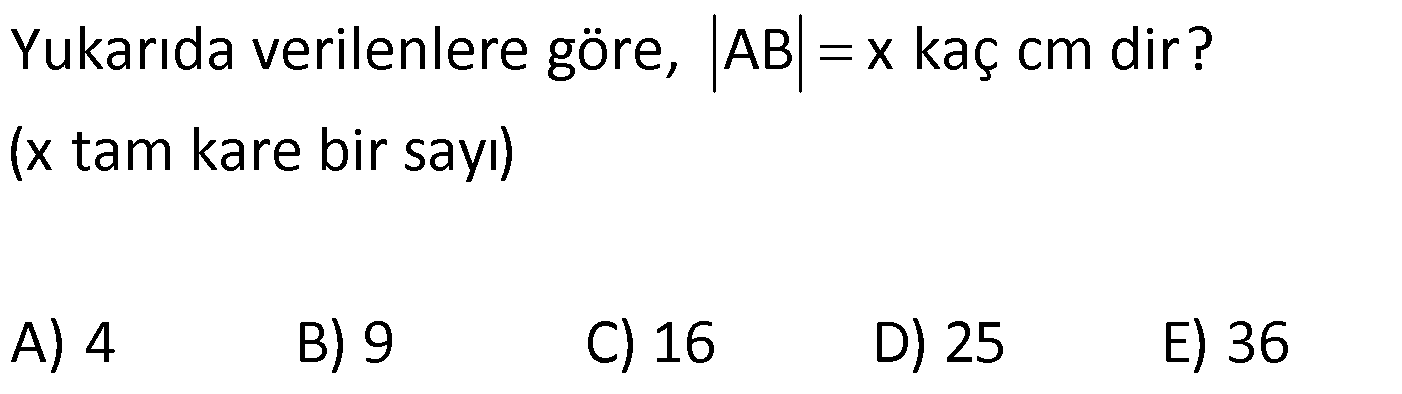
Çözüm için Tıklayınız.
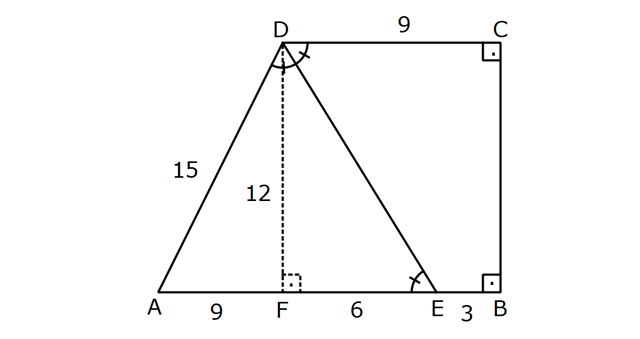
9.SORU
| | | | | |
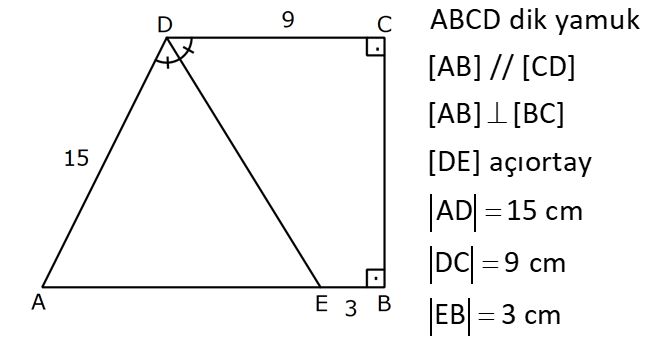
Çözüm için Tıklayınız.
10.SORU
| | | | | |
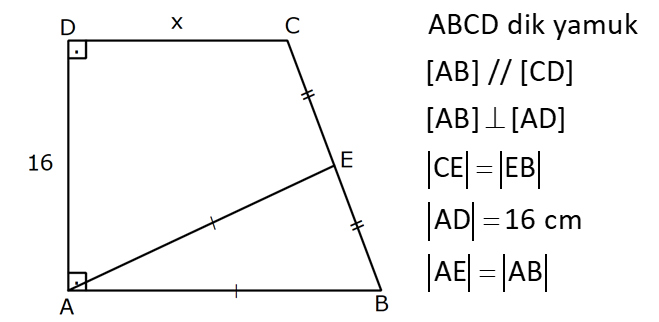
Çözüm için Tıklayınız.
Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
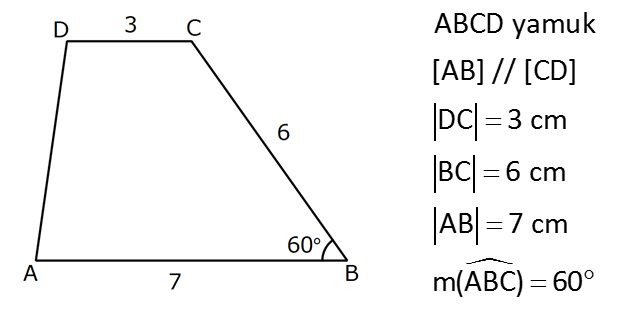
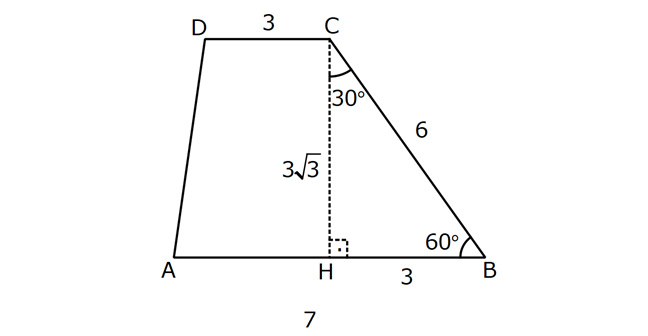
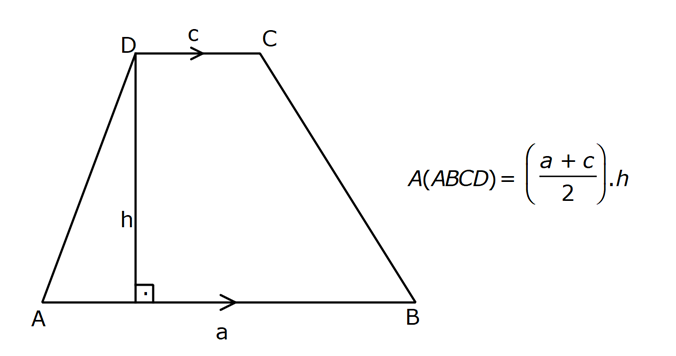
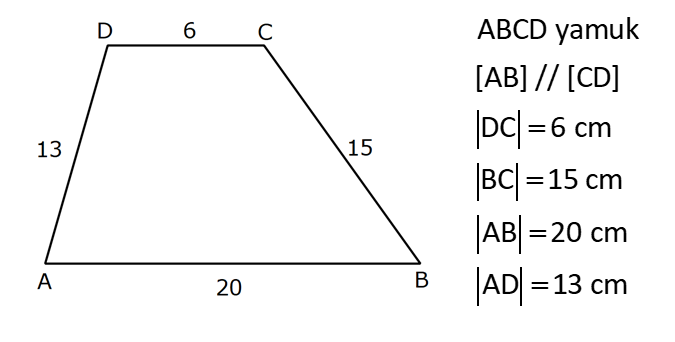
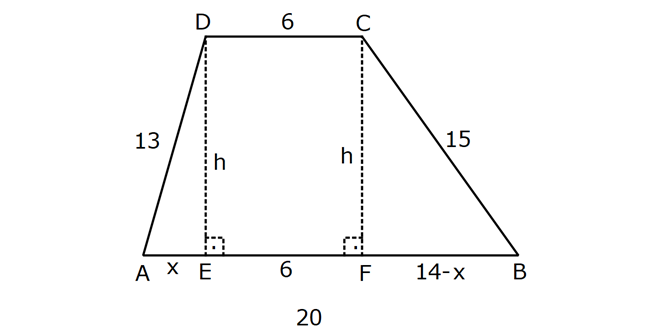
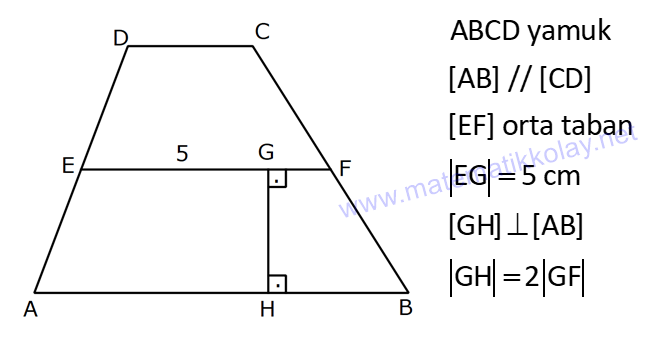
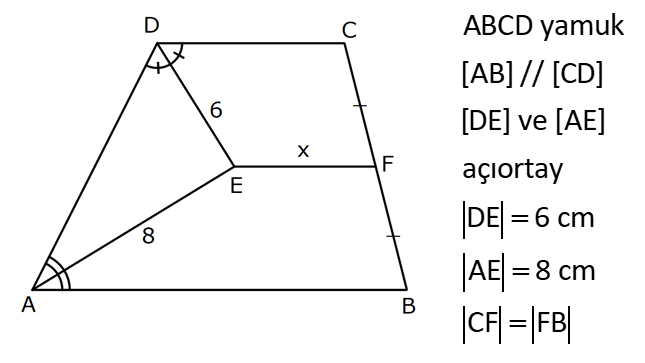
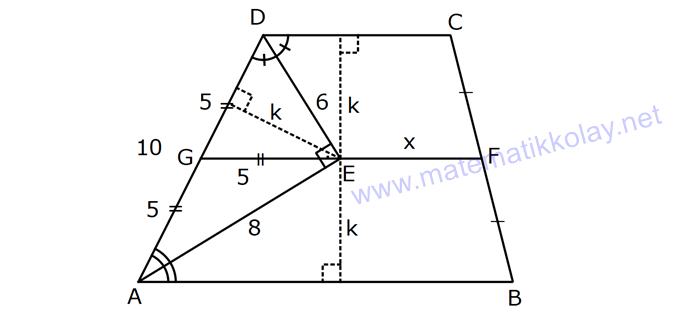
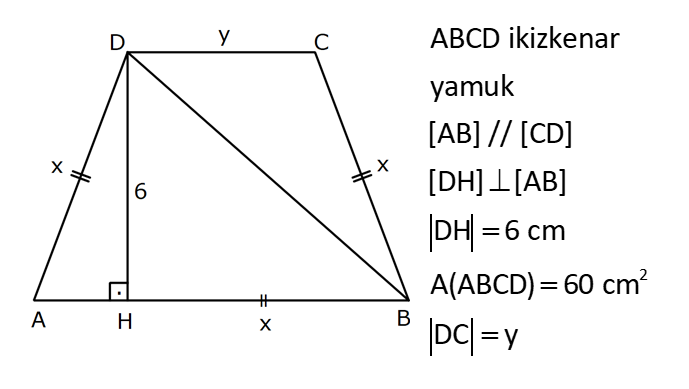
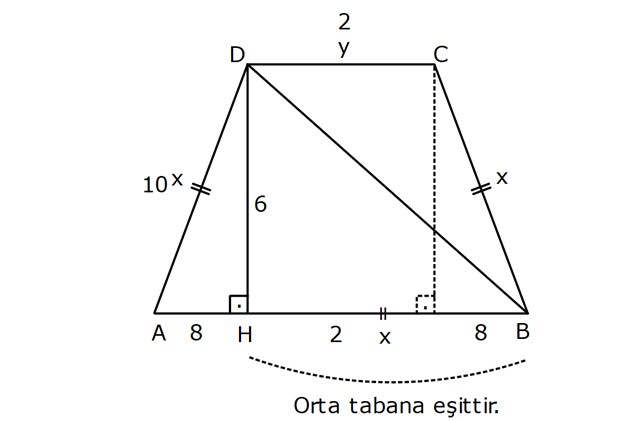
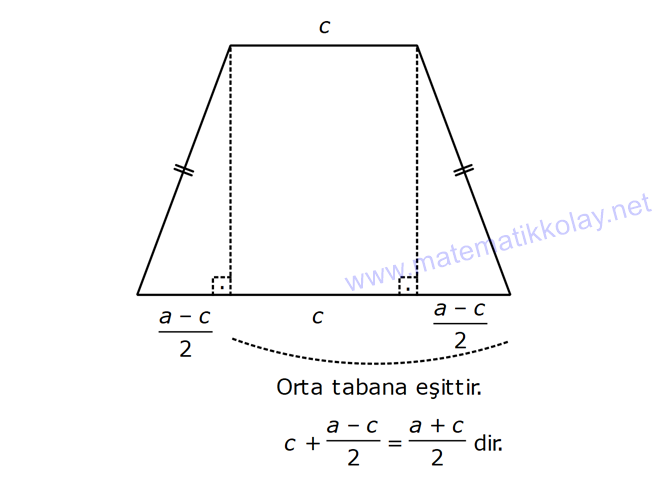
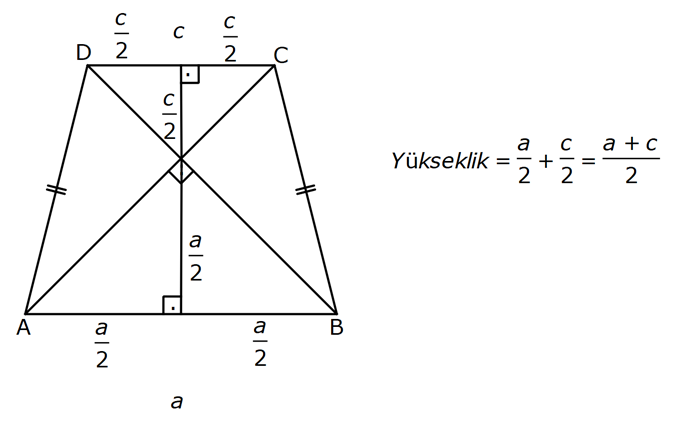
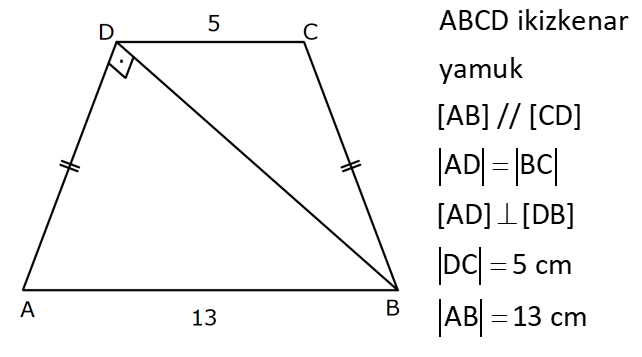
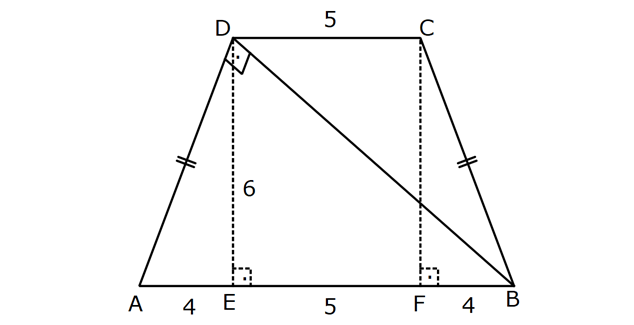
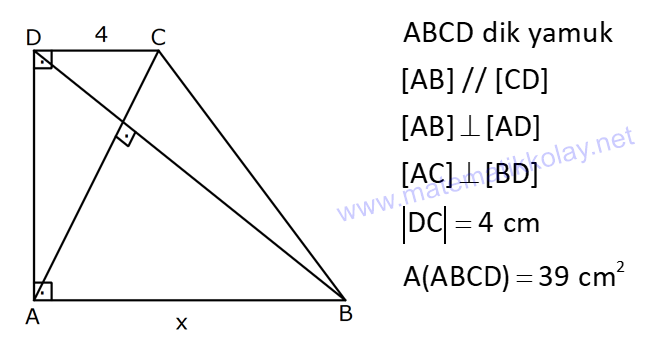
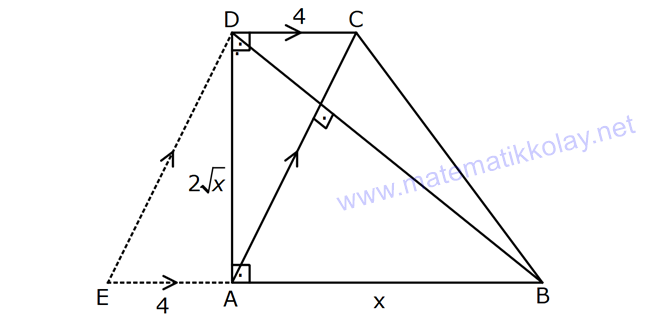
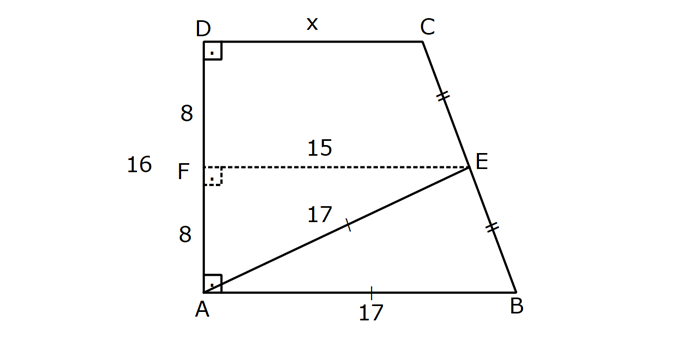
YAMUĞUN ALANI www.matematikkolay.net 1) ABCD yamuk [AB] // [CD] DC 3 cm BC 6 cm AB 7 cm m(ABC) 60 2 Yukarıda verilenlere göre, A(ABCD) kaç cm dir? A) 12 3 B) 15 C) 15 3 D) 18 E) 18 3 ÇÖZÜM: 2 C den dikme indirirsek, 30 – 60 – 90 üçgeni oluşur. CB 6 cm ise, HB 3 cm, CH 3 3 cm olur. Buna göre, 3 7 A(ABCD) 3 3 5 3 3 15 3 cm dir. 2 Cevap : C Alt Taban Üst Taban Yamuğun Alanı Yükseklik 2 Not : 2) ABCD yamuk [AB] // [CD] DC 6 cm BC 15 cm AB 20 cm AD 13 cm 2 Yukarıda verilenlere göre, A(ABCD) kaç cm dir? A) 144 B) 156 C) 160 D) 176 E) 180 ÇÖZÜM: 2 2 2 2 2 2 D ve C’den dikme indirelim. EF 6 cm olur. AE x cm olsun. FB 20 x 6 14 x cm olur. AED üçgeninde pisagordan h 13 x dir. CFB üçgeninde pisagordan h 15 (14 x) dir. Bu ikisini birbirine eşitleyelim. 2 2 2 2 2 2 2 13 x 15 (14 x) 169 x 225 (196 28x x ) 169 x 2 225 196 28x x 2 2 2 2 2 169 29 28x 140 28x x 5 cm dir. h 13 5 h 144 h 12 cm dir. 6 20 A(ABCD) 12 13.12 156 cm buluruz. 2 Cevap : B 3) www.matematikkolay.net ABCD yamuk [AB] // [CD] [EF] orta taban EG 5 cm [GH] [AB] GH 2 GF 2 A(ABCD) 96 cm olduğuna göre, GF kaç cm dir ? 7 9 A) 3 B) C) 4 D) E) 5 2 2 ÇÖZÜM: Orta taban GF x dersek, GH 2x olur. [EF] orta taban olduğundan, yamuğun yüksekliği h 4x olur. DC AB A(ABCD) h 2 96 24 (5 x). 4 2 2 8.( 3) x 24 5x x 0 x 5x 24 0 (x 8)(x 3) x 3 cm buluruz. Cevap : A Bir yamuğun alanı (Orta Taban).(Yükseklik) formülü ile de bulunabilir. Not : 4) ABCD yamuk [AB] / / [CD] [DE] ve [AE] açıortay DE 6 cm AE 8 cm CF FB 2 A(ABCD) 144 cm olduğuna göre, EF x kaç cm dir? A) 6 B) 8 C) 9 D) 10 E) 12 ÇÖZÜM: [AE] ve [DE] açıortayları orta taban üzerinde dik kesi- şirler. AED üçgeni bir 6 – 8 -10 üçgenidir. AD 10 cm olur. Muhteşem üçlüden dolayı GE 5 cm olur. AED üçgeninin yüksekliğini bulalım. 6.Ağu 4 2 10 5 .k 2 24 k dır. 5 Açıortaydan kollara inilen dikmeler birbirine eşit olacağı için, yamuğun yüksekliği 2k dır. A(ABCD) GF .2k 144 6 3 GF 2 24 5 GF 3 GF 15 cm dir. 5 x 15 5 10 cm buluruz. Cevap : D www.matematikkolay.net 5) 2 ABCD ikizkenar yamuk [AB] // [CD] [DH] [AB] DH 6 cm A(ABCD) 60 cm DC y AD HB BC x olduğuna göre, y kaç cm dir? A) 2 B) 3 C) 4 D) 5 E) 6 ÇÖZÜM: 10 İkizkenar yamuk olduğu için, HB uzunluğu orta tabana eşittir. A(ABCD) 6.x 60 6x x 10 cm dir. O halde, ADH üçgeni bir 6 – 8 -10 üçgenidir. AH 8 cm olur. y x 8 2 cm buluruz. Cevap : A Not : 6) 2 Köşegenleri dik kesişen bir ikizkenar yamuğun alanı 45 cm dir. Buna göre, yamuğun orta tabanı kaç cm dir? A) 3 B) 3 3 C) 3 5 D) 6 E) 9 ÇÖZÜM: 2 2 Köşegenleri dik kesişen ikizkenar bir yamuğun yüksekliği orta tabana eşit olacağı için, yamuğun alanı orta tabanın karesine eşit olur. a c Alan 2 Buna göre, a c 45 2 a c 45 3 5 cm dir (Or 2 Not : ta Taban). Cevap: C 7) www.matematikkolay.net ABCD ikizkenar yamuk [AB] // [CD] AD BC [AD] [DB] DC 5 cm AB 13 cm 2 Yukarıda verilenlere göre, A(ABCD) kaç cm dir? A) 35 B) 36 C) 40 D) 42 E) 54 ÇÖZÜM: 2 2 D ve C den dikme indirelim. 13 5 EF 5 cm olur. AE FB 4 cm olur. 2 ADB üçgeninde öklit uygularsak, AE 4.9 AE 6 cm olur. 5 13 A(ABCD) 6 9.6 54 cm dir. Cevap : E 2 8) 2 ABCD dik yamuk [AB] // [CD] [AB] [AD] [AC] [BD] DC 4 cm A(ABCD) 39 cm Yukarıda verilenlere göre, AB x kaç cm dir ? (x tam kare bir sayı) A) 4 B) 9 C) 16 D) 25 E) 36 ÇÖZÜM: 2 [AC] ye paralel olarak [ED] yi çizelim. [DC] ye paralel olarak da [EA] yı çizelim. EA 4 cm olur. EDB üçgeninde öklit yaparsak, AD 4.x AD 2 x cm olur. x 4 A(ABCD) 2 2 9 3 13 x 39 (x 4). x 13.3 (x 4). x x 9 cm olmalıdır. Cevap : B 9) ABCD dik yamuk [AB] // [CD] [AB] [BC] [DE] açıortay AD 15 cm DC 9 cm EB 3 cm 2 Yukarıda verilenlere göre, A(ABCD) kaç cm dir? A) 130 B) 145 C) 162 D) 180 E) 208 ÇÖZÜM: www.matematikkolay.net m(DEA) m(EDC) eşittir (iç ters açı). O halde ADE üçgeni bir ikizkenar üçgendir. AE 15 cm olur. D’den bir dikme indirelim. FE 6 cm olur. AF 15 6 9 cm kalır. AFD üçgeni bir 9 -12 -15 üçgenid ir. DF 12 cm olur. Buna göre, 18 9 27 A(ABCD) 12 2 2 12 6 2 162 cm dir. Cevap : C 10) ABCD dik yamuk [AB] // [CD] [AB] [AD] CE EB AD 16 cm AE AB 2 A(ABCD) 240 cm olduğuna göre, DC x kaç cm dir? A) 11 B) 13 C) 14 D) 15 E) 16 ÇÖZÜM: F noktası [AD] nin orta noktası olsun. AF FE 8 cm olur. A(ABCD) FE . AD 240 FE .16 FE 15 cm dir. AFE üçgeni 8 15 17 üçgenidir. AE AB 17 cm olur. [FE] orta taban olduğu için, x 17 15 30 x 17 x 13 cm bul 2 uruz. Cevap : B
