Soru Sor sayfası kullanılarak Üslü Denklem ve Eşitsizlikler konusu altında Üssün aralığını bulmak ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
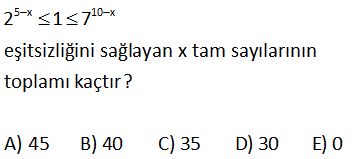

2.SORU


3.SORU
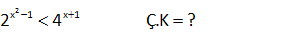

4.SORU
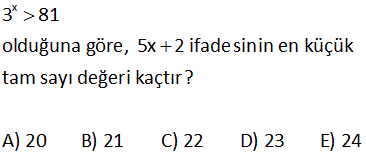

5.SORU

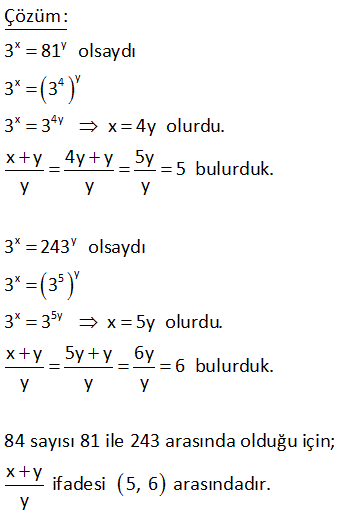
Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Abone olarak daha fazla sayıda soru sorabilirsiniz. Abone olmak için Tıklayın.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Not: Bu sitede yayınlanan çözümler, tamamen bu site için hazırlanmıştır. İzinsiz olarak yayınlanıp, çoğaltılması yasaktır.
5 x 10 x 2 1 7 eşitsizliğini sağlayan x tam sayılarının toplamı kaçtır? A) 45 B) 40 C) 35 D) 30 E) 0 5 x 10 x 5 x 5 x 0 10 x 0 10 x Çözüm: 2 1 7 Eşitsizği iki parça halinde çözelim; 2 1 2 2 5 x 0 5 x dir. 1 7 7 7 0 10 x x 10 dur. Buradan; 5 x 10 dur. Bu aralarıktaki x değerlerinin toplamı; 5+6 7 8 9 10 45 buluruz. 13 x 7 163 olduğuna göre, x için aşağıdakilerden hangisi doğrudur? A) 2 x 3 B) 3 x 4 C) 4 x 5 D) 5 x 6 E) 6 x 7 2 3 Çözüm: 7 49 7 343 163 sayısı da bu iki sayının arasındadır. Buna göre x, 2 ile 3 arasında olmalıdır. Cevap: 2 x 3 20 2 x 1 x 1 2 4 Ç.K ? 2 2 x 1 x 1 x 1 2x 2 2 2 Çözüm: 2 4 2 2 x 1 2x 2 x 2x 3 0 (x 3)(x 1) 0 x 1 ile 3 arasında olmalıdır. Ç.K ( 1,3) 32 x 3 81 olduğuna göre, 5x 2 ifadesinin en küçük tam sayı değeri kaçtır? A) 20 B) 21 C) 22 D) 23 E) 24 x x 4 Çözüm: 3 81 3 3 x 4 tür. Burada x 5 yazmak hata olur. Çünkü x’in tam sayı olduğu belirtilmemiş. x 4 ifadesinde her tarafı 5 ile çarpalım. 5x 20 her tarafa 2 ekleyelim. 5x 2 22 olur . 5x 2 ifadesinin en küçük tam sayı değeri 23 tür.77 x y x ve y sıfırdan farklı reel sayılardır. 3 84 x y olduğuna göre, oranı aşağıdaki aralık – y lardan hangisinde bulunur? A) 1, 2 B) 2, 3 C) 3, 4 D) 4, 5 E) 5, 6 x y x 4 y x 4y x y x 5 y x 5y Çözüm: 3 81 olsaydı 3 3 3 3 x 4y olurdu. x y 4y y 5y 5 bulurduk. y y y 3 243 olsaydı 3 3 3 3 x 5y olurdu. x y 5y y 6y 6 bulurduk. y y y 84 sayısı 81 ile 243 arasında olduğu için; x y ifad yesi 5, 6 arasındadır. 87

