Soru Sor sayfası kullanılarak Üslü Denklem ve Eşitsizlikler konusu altında 1’e eşit durumlar ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
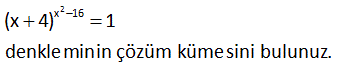

2.SORU


3.SORU
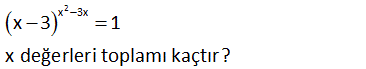

4.SORU
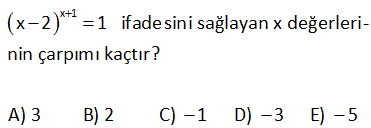

Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Abone olarak daha fazla sayıda soru sorabilirsiniz. Abone olmak için Tıklayın.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Not: Bu sitede yayınlanan çözümler, tamamen bu site için hazırlanmıştır. İzinsiz olarak yayınlanıp, çoğaltılması yasaktır.
2 x 16 (x 4) 1 denkleminin çözüm kümesini bulunuz. 2 x 16 2 Çözüm: (x 4) 1 3 farklı durumda 1’e eşit olur. 1.durum: Üs 0 dır. (Taban 0) x 16 0 (x 4)(x 4) 0 x 4 tür. (x 4 olamaz. Tabanı 0 yapar.) 2.durum: Taba 2 n 1 dir. x 4 1 x 3 tür. 3.durum: Taban 1 ve (Üs çift olmalı) x 4 1 x 5 x 5 için, üs ( 5) 16 25 16 9 (Çift değil) Buna göre Ç.K { 3, 4} buluruz. 26 x 4 x 3 1 denklemini sağlayan farklı x doğal sayılarının toplamı kaçtır? x 4 n 2n 0 Çözüm: x 3 1 3 durum vardır. I.durum:1 1 dir. II.durum: ( 1) 1 dir. III.durum: a 1 dir.(a 0) I.durum: x 3 1 x 1 3 4 tür. II.durum: x 3 1 x 1 3 2 Şimdi bulduğumuz değeri x 4 ifadesinde x yerine yazmal ıyız. Eğer x değeri burayı çift yapamazsa koşul sağlanmaz. x 4 2 4 6 sayısı çifttir. O halde x 2 olur. III.durum: x 4 0 x 4 bu değer doğalsayı olmadığından alamayız. x değerlerinin toplamı 4 2 6 buluruz.58 2 x 3x x 3 1 x değerleri toplamı kaçtır? 2 x 3x a a 2 2 Çözüm: x 3 1 1.durum: 1 1 dir x 3 1 x 4 olabilir. 2.durum: a çift sayı ise 1 1 dir x 3 1 x 2 dir. x 2 için üs ne olur,bakalım x 3x 2 3 2 4 6 2 çift sayıdır. Sağladı. x 2 ol 0 2 abilir. 3.durum: a 0 değilse; a 1 dir. x 3x 0 x x 3 0 x 0 veya x 3 tür. x 0 olduğunda taban x 3 0 3 3 tür. x 3 olduğunda taban 3 3 0 dır. Alamayız. x 0 olabilir. O halde; x değerleri toplamı 4 2 0 6 buluruz. 86 x 1 x 2 1 ifadesini sağlayan x değerleri – nin çarpımı kaçtır? A) 3 B) 2 C) 1 D) 3 E) 5 x 1 n 2n Çözüm: x 2 1 I.1 1 dir. 1’in tüm kuvvetleri 1 dir. x 2 1 x 3 tür. II. 1 1 dir. 1’in çift kuvvetleri 1 dir. x 2 1 x 1 dir. Şimdi x 1 değeri üstünü çift yapıyor mu ona bakmalıyız. x 1 1 1 2 çift. O ha 0 lde x 1 değerini de alırız. 0’dan farklı bütün sayıların III. a 1 0. kuvveti 1 dir. x 1 0 x 1 dir. x 2 1 2 3 0’dan farklı O halde x 1 değeri de sağlar. 3.1. 1 3 bulunur.

