Üçgende Açıortay

1.Sayfa için Tıklayınız.

11.SORU (FEN LİSESİ)

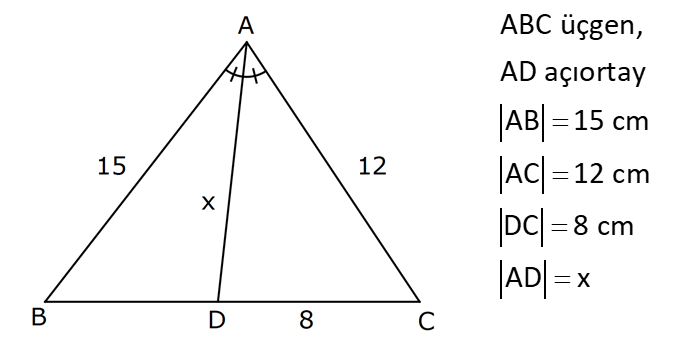
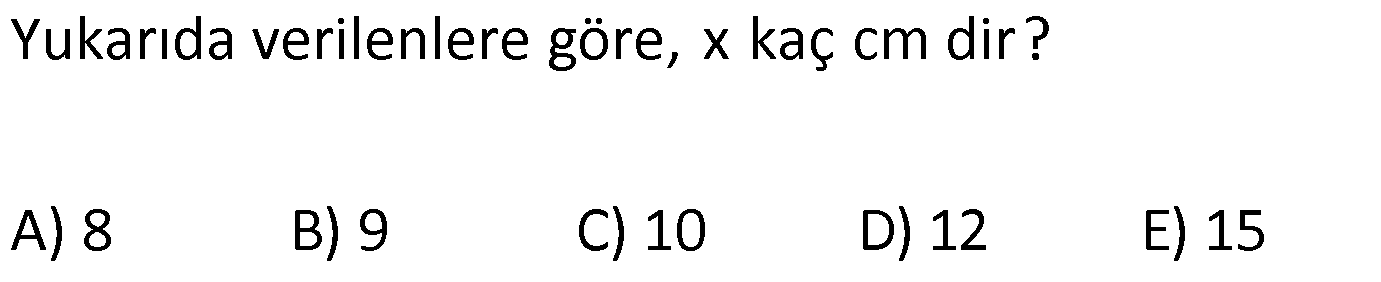
Çözüm için Tıklayınız.

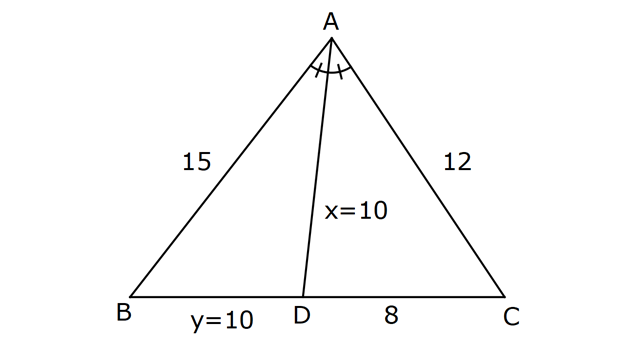
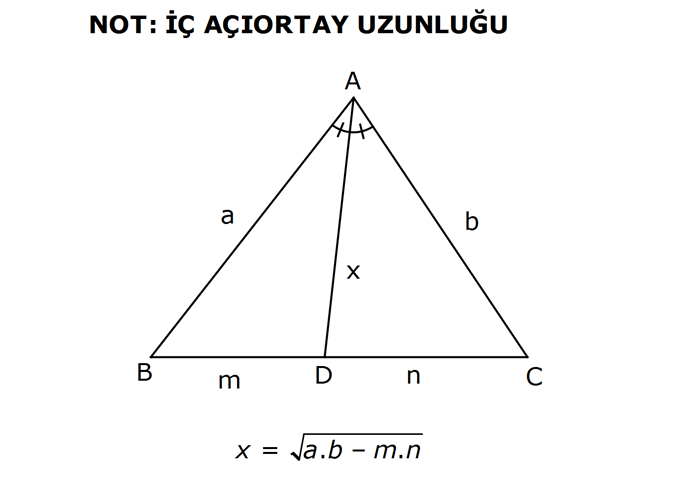
12.SORU (FEN LİSESİ)


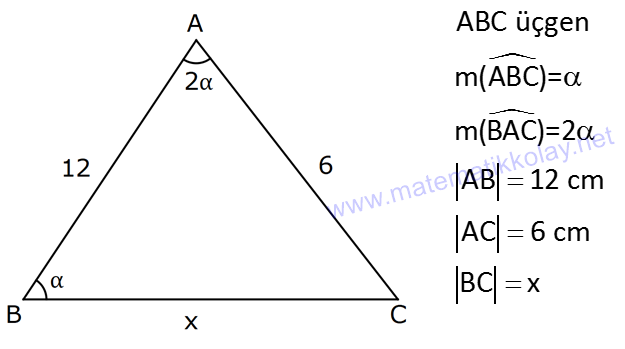
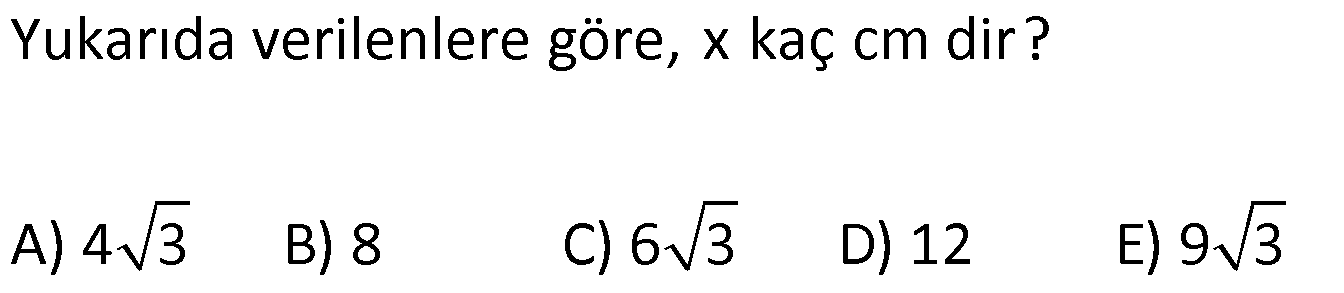
Çözüm için Tıklayınız.

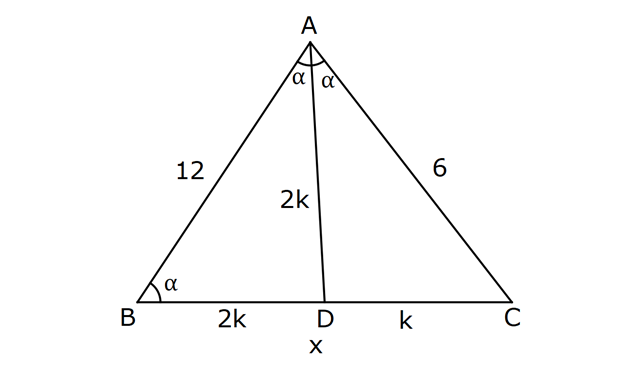
13.SORU

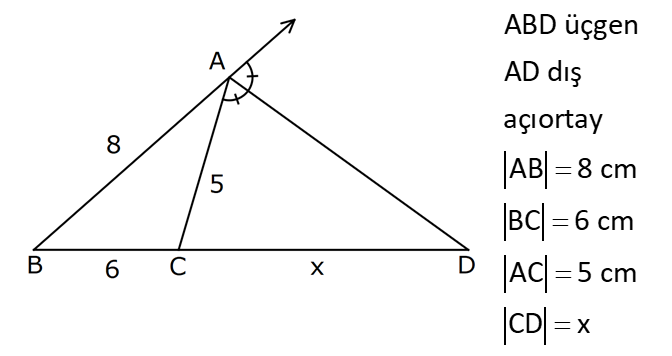
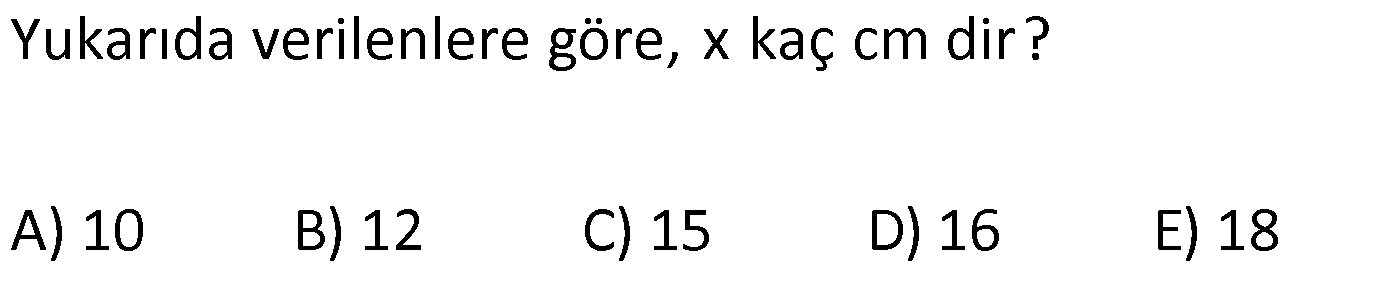
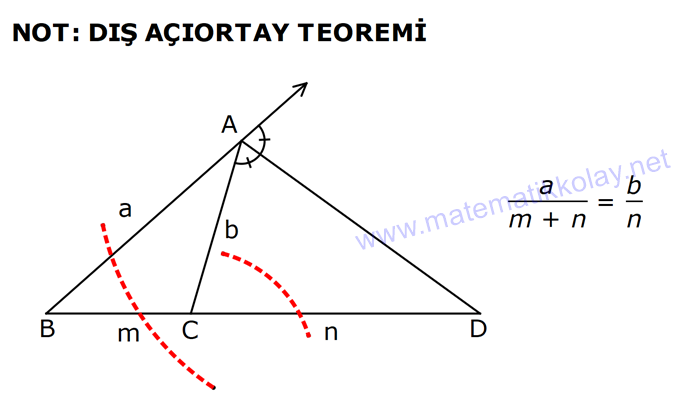
Çözüm için Tıklayınız.

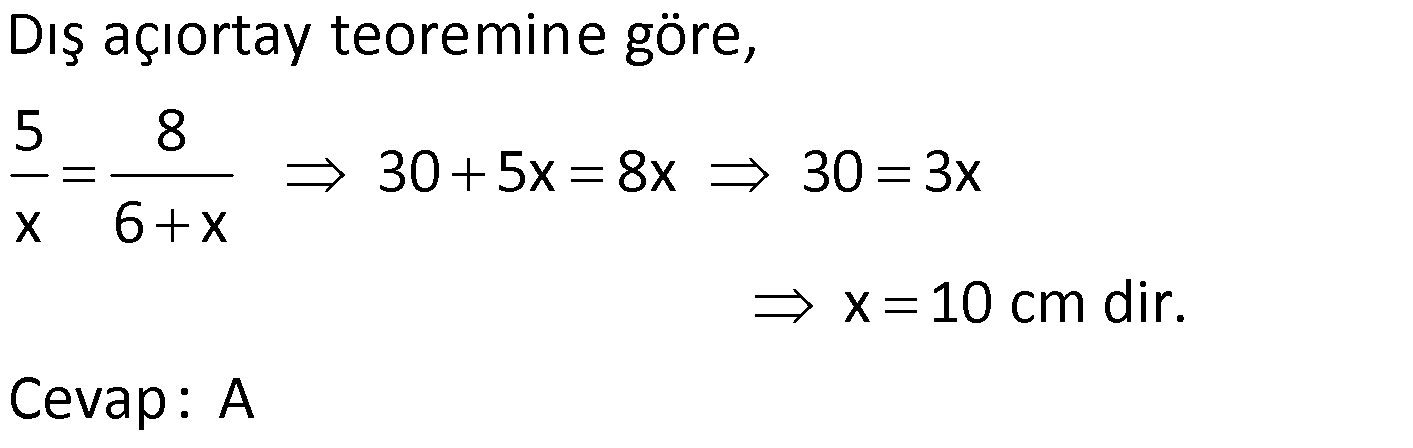
14.SORU

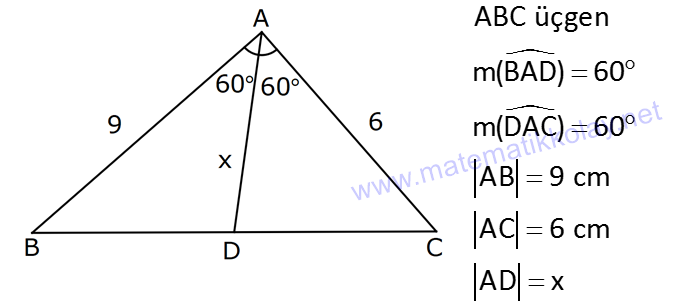
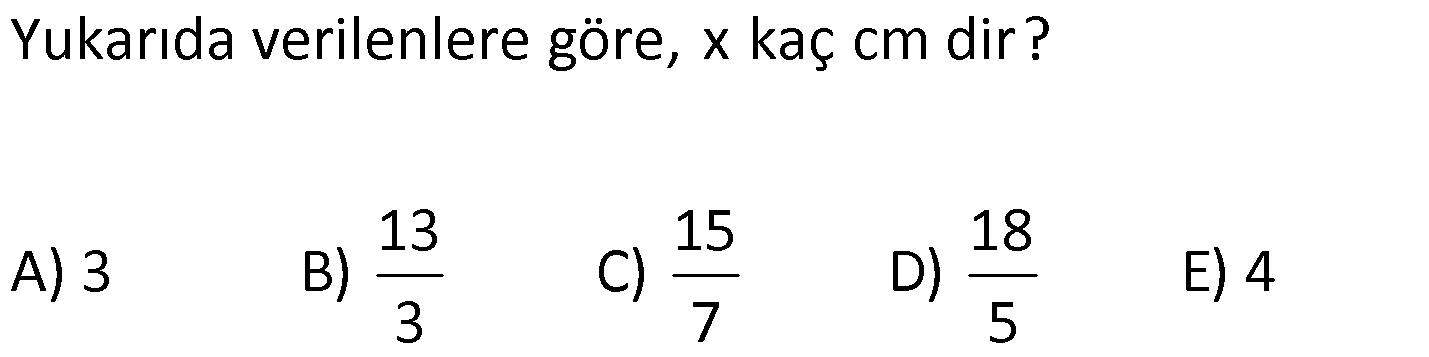
Çözüm için Tıklayınız.

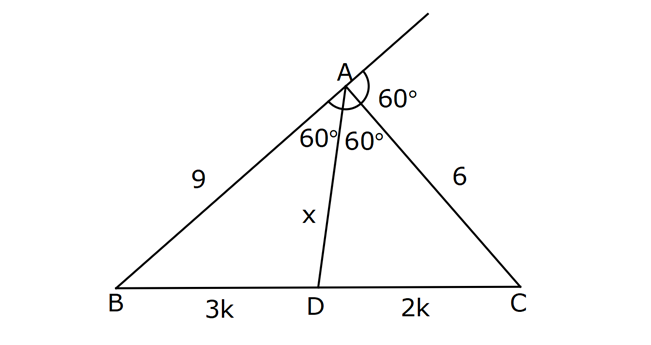
15.SORU

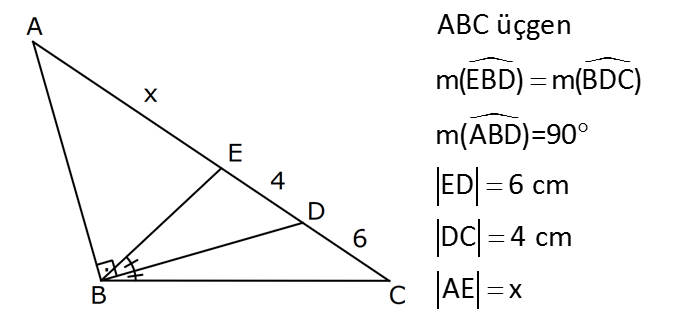
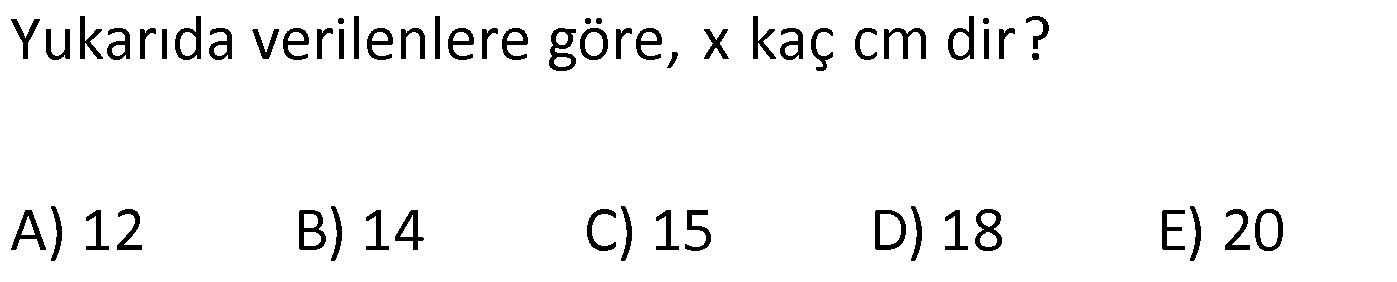
Çözüm için Tıklayınız.

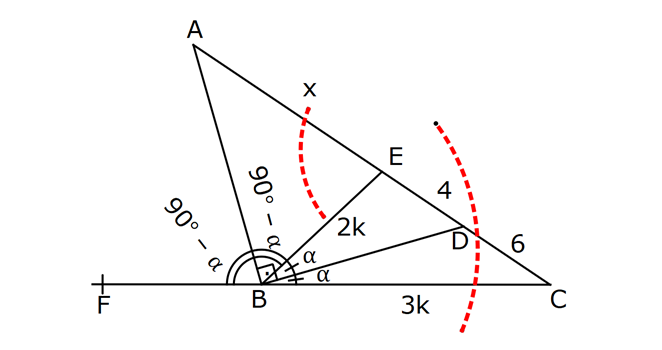
16.SORU

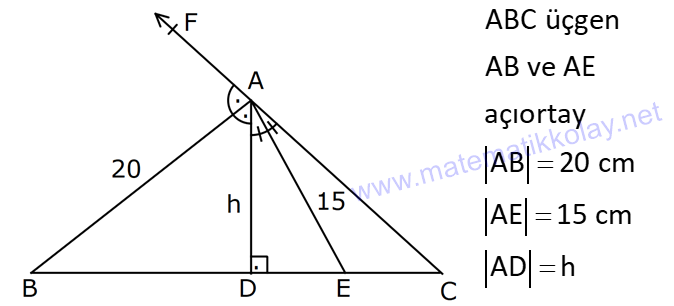
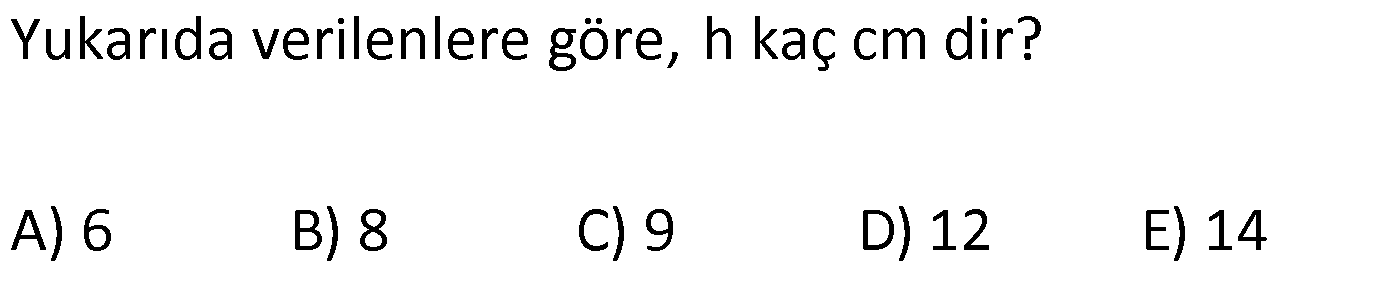
Çözüm için Tıklayınız.

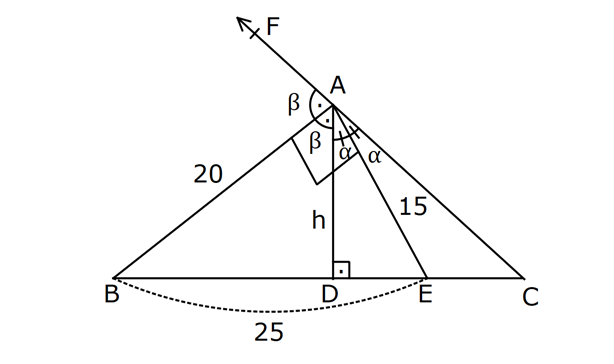
17.SORU (FEN LİSESİ)

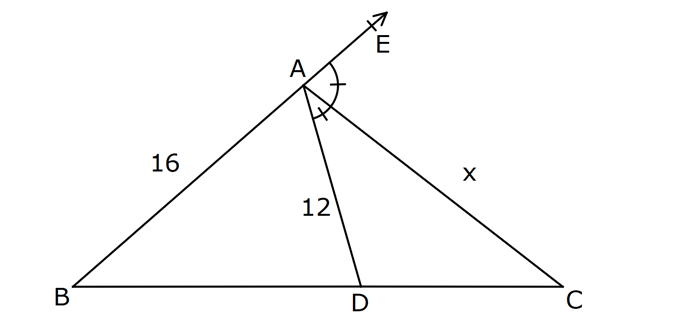
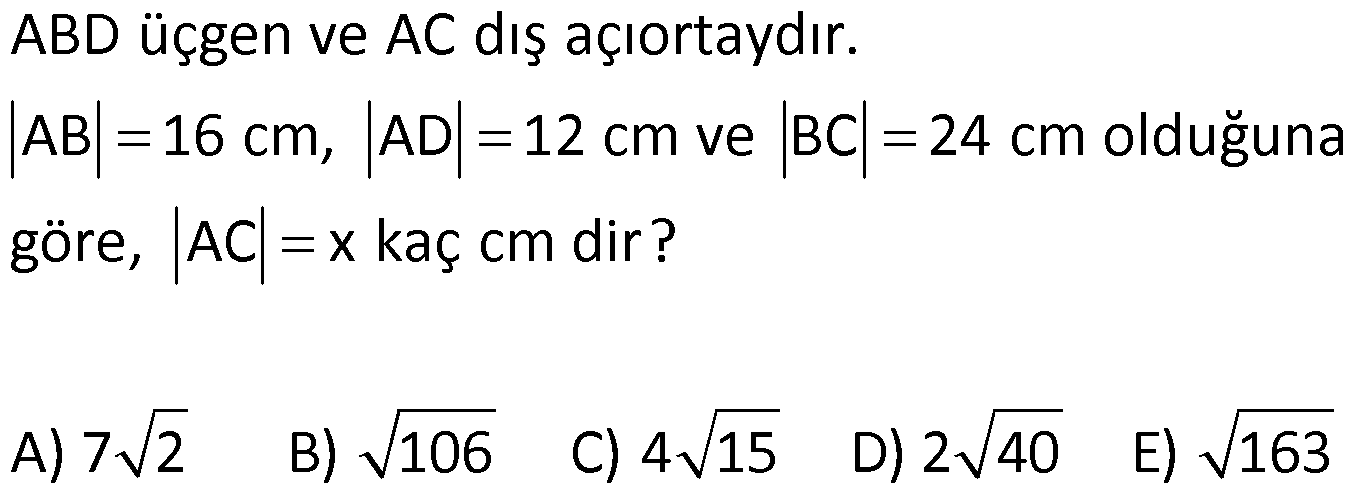
Çözüm için Tıklayınız.

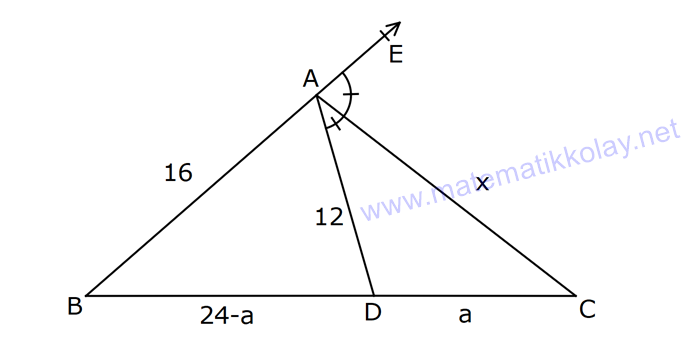
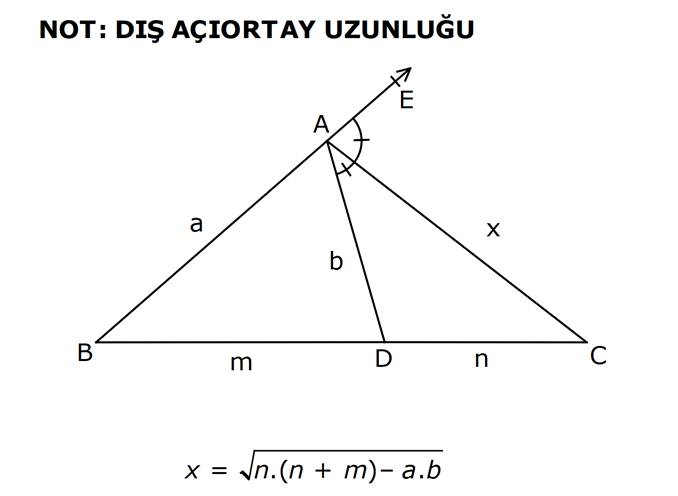
18.SORU (FEN LİSESİ)

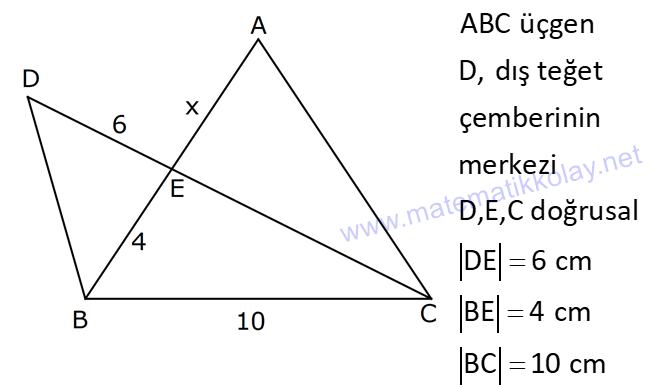
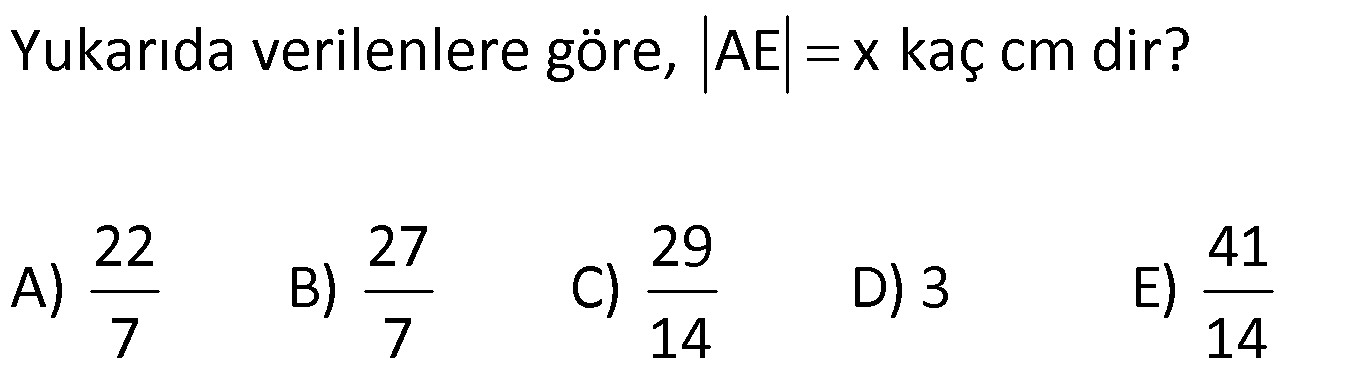
Çözüm için Tıklayınız.

Sorular Bitti. Konu Anlatımı veya Daha Fazla soru için Tıklayabilirsiniz.
Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.) 11) (FEN LİSESİ) ABC üçgen, AD açıortay AB 15 cm AC 12 cm DC 8 cm AD x Yukarıda verilenlere göre, x kaç cm dir? A) 8 B) 9 C) 10 D) 12 E) 15 ÇÖZÜM: www.matematikkolay.net AD açıortayına göre, 15 5 12 BD 3 8 2 BD 5.2 10 cm dir. İç açıortayın uzunluğunu formül ile bulalım. x 15.12 10.8 180 80 100 10 cm dir. Cevap : C 12) (FEN LİSESİ) ABC üçgen m(ABC)= m(BAC)=2 AB 12 cm AC 6 cm BC x Yukarıda verilenlere göre, x kaç cm dir? A) 4 3 B) 8 C) 6 3 D) 12 E) 9 3 ÇÖZÜM: AD açıortayını çizelim. ABD ikizkenar üçgen olur. AD açıortayına göre, 12 2 6 BD 2 2 2 2 2 BD 2k, DC k diyebiliriz. DC ABD ikizkenar üçgen olduğundan, AD 2k dır. Açıortay formülünden, 2k 12.6 2k.k 2k 72 2k 4k 72 2k 6k 72 k 12 k 2 3 tür. x 3k 3.2 3 6 3 cm buluruz. Cevap : C 13) ABD üçgen AD dış açıortay AB 8 cm BC 6 cm AC 5 cm CD x Yukarıda verilenlere göre, x kaç cm dir? A) 10 B) 12 C) 15 D) 16 E) 18 ÇÖZÜM: www.matematikkolay.net Dış açıortay teoremine göre, 5 8 30 5x 8x 30 3x x 6 x x 10 cm dir. Cevap: A 14) ABC üçgen m(BAD) 60 m(DAC) 60 AB 9 cm AC 6 cm AD x Yukarıda verilenlere göre, x kaç cm dir? 13 15 18 A) 3 B) C) D) E) 4 3 7 5 ÇÖZÜM: AD iç açıortayına göre, 9 3 6 BD 2 BD 3k, DC 2k diyebiliriz. DC A noktasındaki dış açı 60 olduğundan, AC doğrusu da, ABD üçgeni için bir dış açıortaydır. 9 5 k x 2 k 18 x cm dir. Cevap : D 5 15) ABC üçgen m(EBD) m(BDC) m(ABD)=90 ED 6 cm DC 4 cm AE x Yukarıda verilenlere göre, x kaç cm dir? A) 12 B) 14 C) 15 D) 18 E) 20 ÇÖZÜM: BD doğrusu, BEC üçgeni için bir iç açıortaydır. BC 6 3 BE 4 2 BE 2k, BC 3k dır. m(DBC) olsun. m(EBD) olur. m(ABE) 90 olur. m(ABF) 90 olur. (Doğru Açı 180 dir.) BA doğrusu, BEC üçgeni için bir dış açıortaydır. 3 k 2 k 10 x 3x 20 2x x 20 cm dir. x Cevap : E 16) www.matematikkolay.net ABC üçgen AB ve AE açıortay AB 20 cm AE 15 cm AD h Yukarıda verilenlere göre, h kaç cm dir? A) 6 B) 8 C) 9 D) 12 E) 14 ÇÖZÜM: Açıortay açılarına ve diyelim. 2 2 180 90 olur. m(BAE) 90 dir. O halde, ABE üçgeni bir 15-20 -25 üçgenidir. (3k – 4k – 5k) ABE üçgeninin alanını hem dik kenarlardan, hem de yükseklik ve tabandan bulabiliriz. İkisini birbi￾rine eşitleyelim. 20 4 . 15 3 2 25 5 .h 2 h 4.3 12 cm dir. Cevap: D 17) (FEN LİSESİ) ABD üçgen ve AC dış açıortaydır. AB 16 cm, AD 12 cm ve BC 24 cm olduğuna göre, AC x kaç cm dir? A) 7 2 B) 106 C) 4 15 D) 2 40 E) 163 ÇÖZÜM: AC dış açıortayına göre, 12 3 16 a 4 24 6 a 3.6 18 cm dir. BD 24 18 6 cm dir. Dış açıortay uzunluk formülüne göre, x 18.24 16.12 432 192 240 4 15 cm dir. Cevap : C www.matematikkolay.net 18) FEN LİSESİ ABC üçgen D, dış teğet çemberinin merkezi D,E,C doğrusal DE 6 cm BE 4 cm BC 10 cm Yukarıda verilenlere göre, AE x kaç cm dir? 22 27 29 41 A) B) C) D) 3 E) 7 7 14 14 ÇÖZÜM: Bir üçgende iki dış açıortay ve bir iç açıortay bir noktada kesişir. Bu nokta, dış teğet çemberinin merkezidir. Bu nedenle AD ve BD dış açıortay, ED ise bir iç açıor – taydır. BD dış açıortayına göre, 10 5 4 6 y 2 6 3 6 y 15 y 9 cm dir. EC iç açıortayına göre, AC 10 AE 5 4 2 AC 5k, AE 2k diyebiliriz. İç açıortayın uzunluk formülünden, 9 5k.10 2k.4 9 50k 8k 9 42k 81 27 42 14 27 k k tür. 14 x 2k 2 27 14 7 27 cm dir. Cevap : B 7
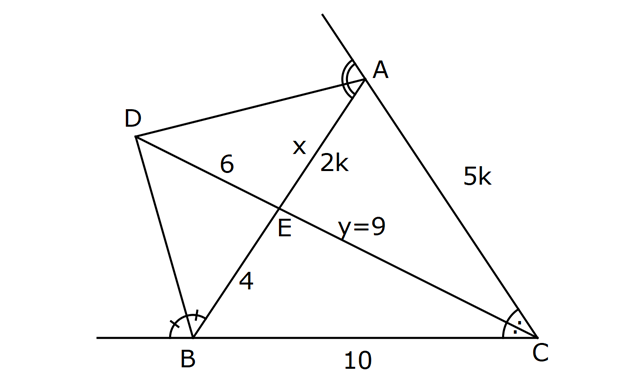
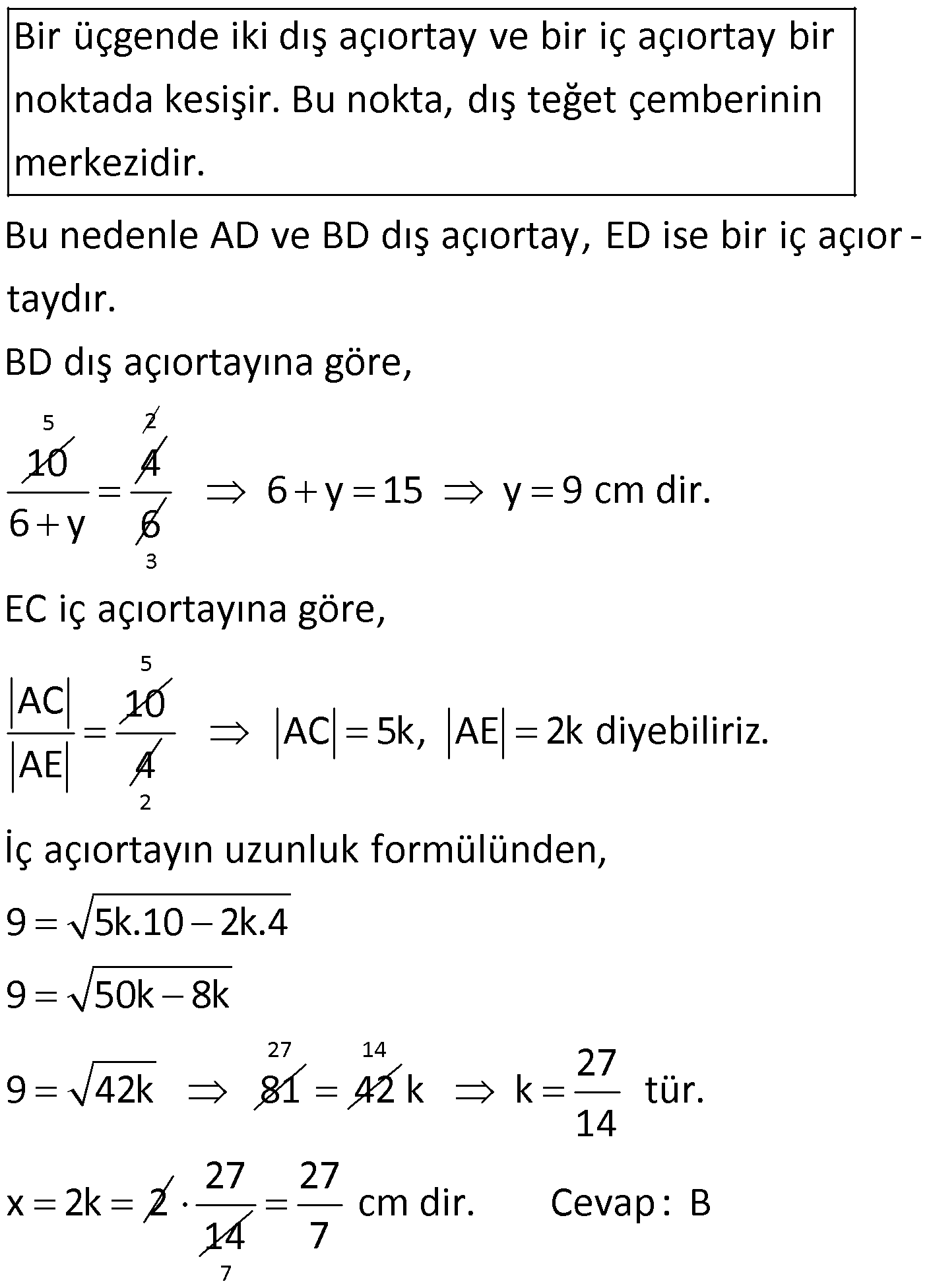
Sayfalar: 1 2

“Üçgende Açıortay” üzerine 3 yorum

    • Uyarınız için teşekkürler. Soru yerine yanlışlıkla çözümü gelmiş. Şimdi düzeltildi.

Yorum yapın