 Bu bölümde Üçgende Açıortay ile ilgili 18 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
Bu bölümde Üçgende Açıortay ile ilgili 18 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
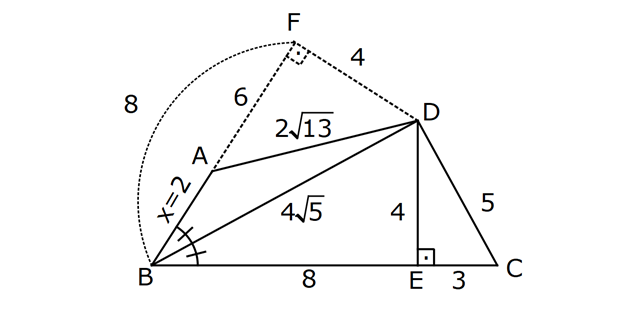
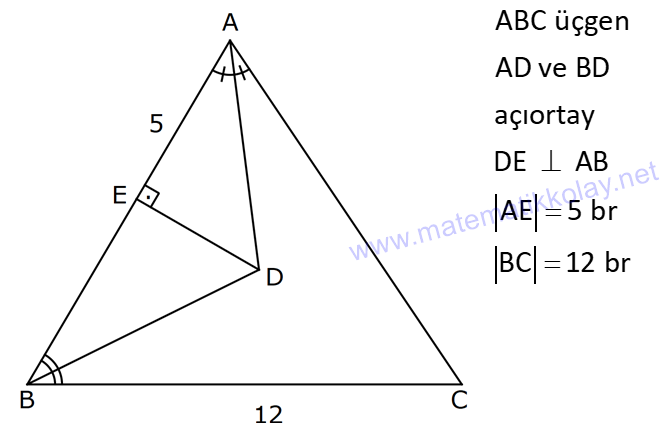
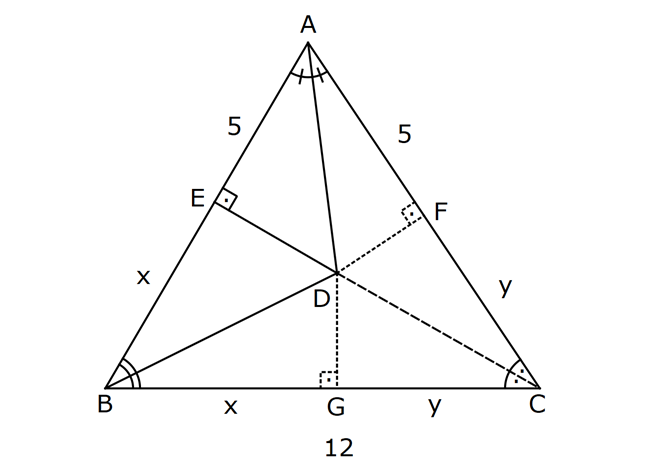
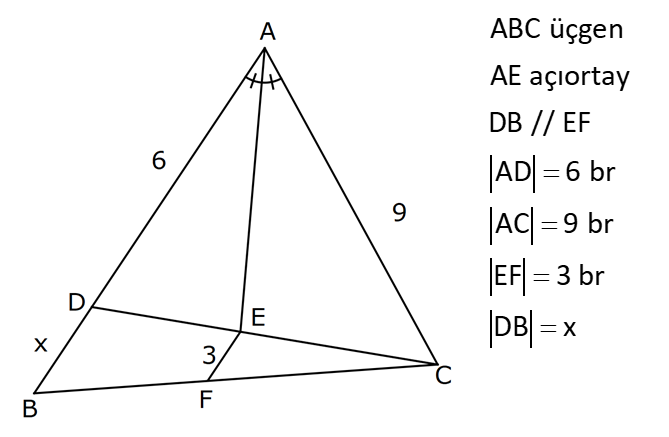
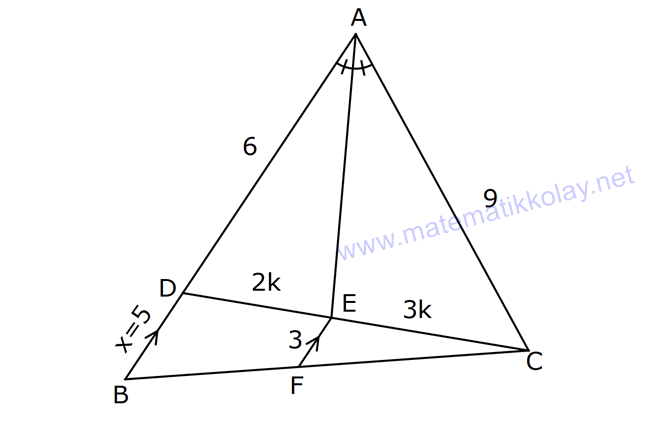
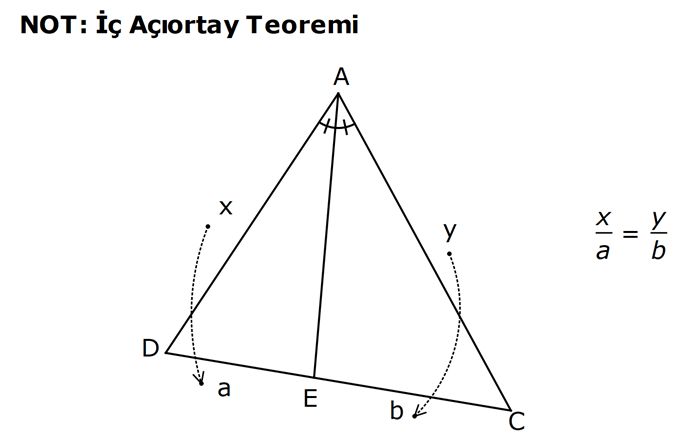
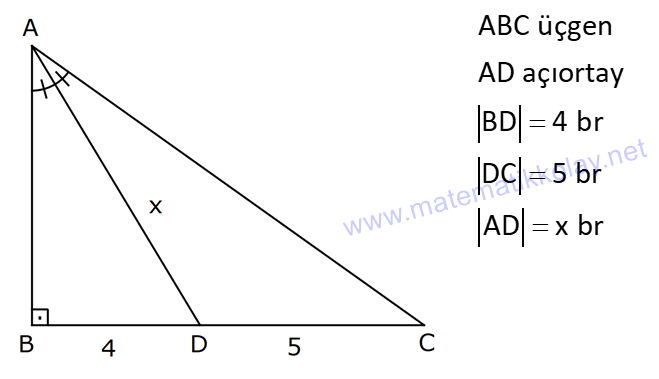
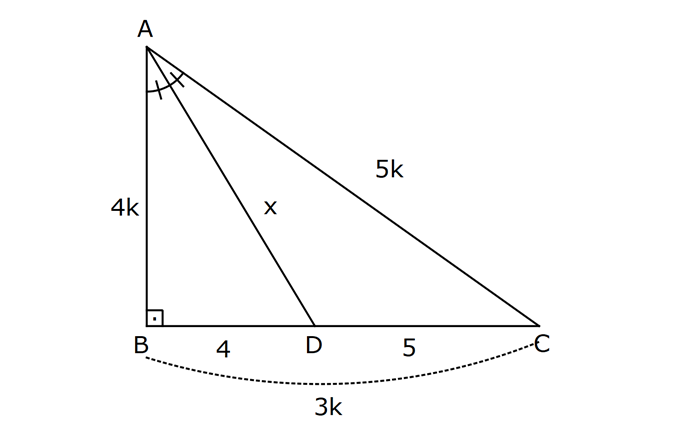
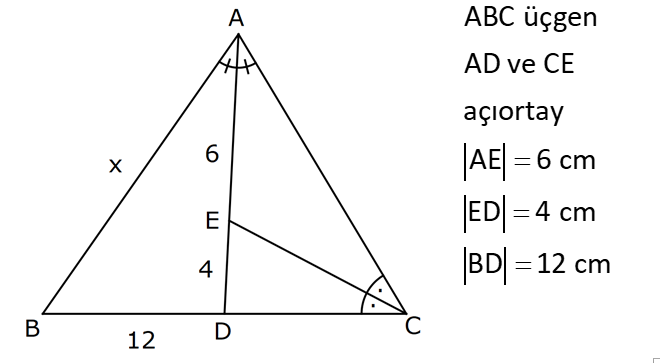
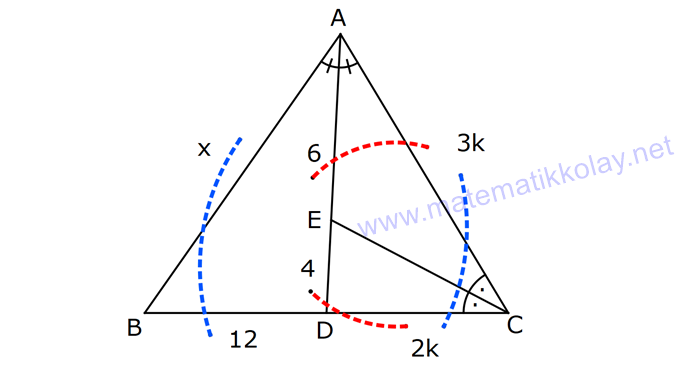
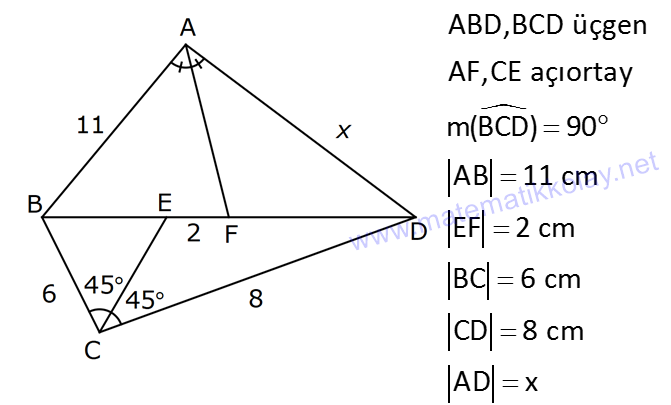
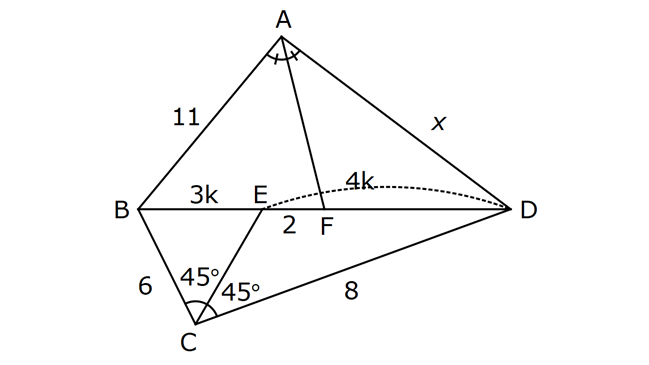
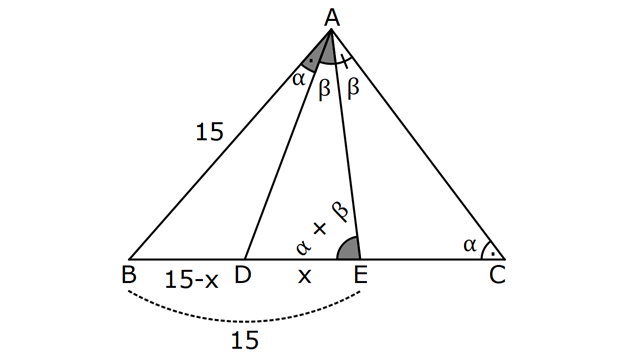
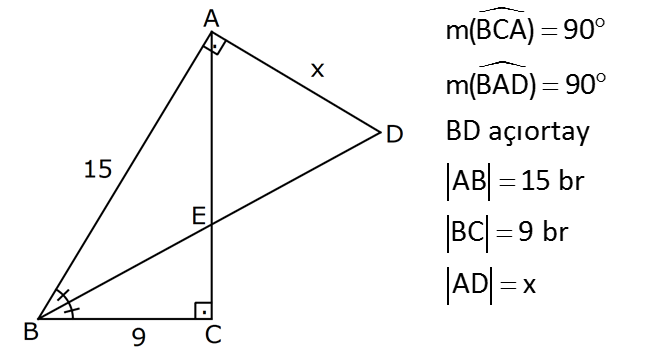
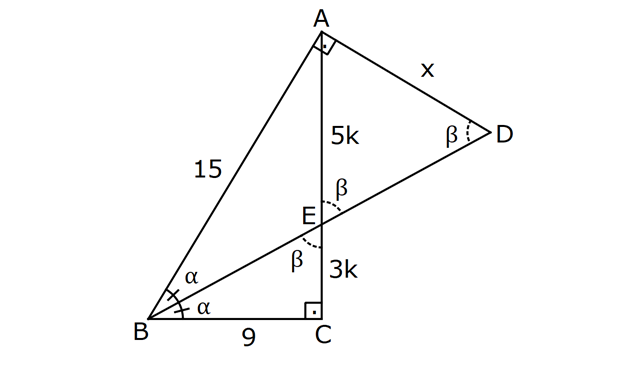
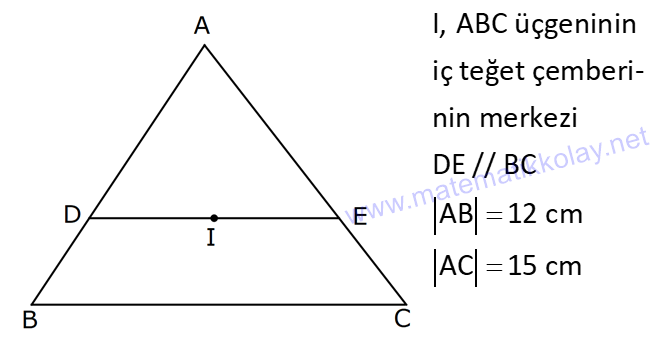
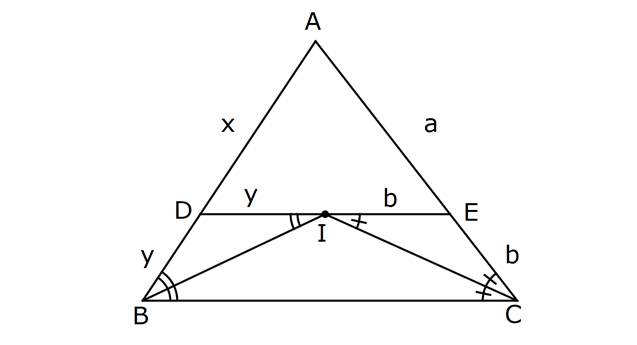
ÜÇGENDE AÇIORTAY www.matematikkolay.net 1) BD açıortay DE BC EC 3 cm DC 5 cm BD 4 5 cm AD 2 13 cm AB x cm Yukarıda verilenlere göre x kaç cm dir? A) 1 B) 2 C) 4 D) 6 E) 8 ÇÖZÜM: 2 2 2 2 2 DEC üçgeni bir 3- 4 – 5 üçgenidir. DE 4 cm BDE üçgeninde pisagor yapalım. 4 5 4 BE 80 16 BE BE 64 BE 8 cm dir. Açıortay üzerinden bir noktadan kollara inilen dikmelerin uzunlukları birbirin 2 2 2 2 2 e eşittir. FD 4 cm dir. Bu dikmelerin kollarda ayırdığı uzunluklar da birbirine eşittir. BF 8 cm dir. AFD üçgeninde pisagor yapalım. 2 13 4 AF 52 16 AF AF 36 AF 6 cm dir. Buna göre, x 8 6 2 cm dir. Cevap : B 2) ABC üçgen AD ve BD açıortay DE AB AE 5 br BC 12 br Yukarıda verilenlere göre, ABC üçgeninin çevresi kaç br dir? A) 24 B) 26 C) 28 D) 32 E) 34 ÇÖZÜM: Bir üçgende açıortaylar bir noktada kesişir. Bu sebeple DC doğrusu da açıortay olur. Açıortayın kollarda ayırdığı uzunluklar birbirine eşittir. Bu sebeple AF 5 br dir. (AD açıortayının kolu) BE x derse 12 k BG x olur. (BD açıortayının kolu) FC y dersek GC y olur. (DC açıortayının kolu) x y 12 olduğuna göre, Ç(ABC) 2(5 x y) 2.17 34 br dir. Cevap : E www.matematikkolay.net 3) ABC üçgen AE açıortay DB // EF AD 6 br AC 9 br EF 3 br DB x Yukarıda verilenlere göre, x kaç br dir? A) 2 B) 3 C) 4 D) 5 E) 6 ÇÖZÜM: İç açıortay teoremine göre, 6 2 9 DE 3 dir. DE 2k, EC 3k diyebiliriz. EC Temel benzerlik teoremine göre, ECF üçgeni ile DCB üçgeni arasında benzerlik kurabiliriz. 3 3k x 5 br dir. Cevap : D x 5k 4) ABC üçgen AD açıortay BD 4 br DC 5 br AD x br Yukarıda verilenlere göre, x kaç br dir? A) 4 B) 4 5 C) 4 10 D) 8 E) 8 2 ÇÖZÜM: www.matematikkolay.net 2 2 ABC üçgeninde iç açıortay teoremine göre, AB AC tir. AB 4k, AC 5k diyebiliriz. 4 5 ABC üçgeni bir 3k – 4k – 5k üçgenidir. 3k (4 5) 3k 9 k 3 tür. AB 4.3 12 br dir. ABD üçgeninde pisagor yaparsak, x 12 4 2 144 16 160 x 160 4 10 br dir. Cevap: C 5) ABC üçgen AD ve CE açıortay AE 6 cm ED 3 cm BD 12 cm Yukarıda verilenlere göre, x kaç cm dir? A) 24 B) 20 C) 18 D) 16 E) 12 ÇÖZÜM: CE açıortayını kullanalım. AC 6 2 DC 3 AC 2k, DC k diyebiliriz. Sonra AD açıortayını kullanalım. x 2k 12 k x 24 cm dir. Cevap : A 6) ABD,BCD üçgen AF,CE açıortay m(BCD) 90 AB 11 cm EF 2 cm BC 6 cm CD 8 cm AD x Yukarıda verilenlere göre, x kaç cm dir? A) 4,5 B) 5 C) 6,5 D) 8 E) 9,5 ÇÖZÜM: www.matematikkolay.net BCD üçgeni de bir 6 – 8 -10 üçgenidir. BD 10 CE açıortayına göre, BE 3k, ED 4k diyebiliriz. 10 3k 4k 10 7k 10 k dir. 7 10 30 BE 3 dir. 7 7 30 30 14 44 BF 2 dir. 7 7 7 10 40 14 26 FD 4 2 dir. 7 7 7 BF açıortayı na göre, 11 44 7 x 26 7 11 44 4 2 x 26 13 2x 13 x 6,5 cm Cevap : C 7) ABC üçgen AF DC BD 4 cm BF 8 cm FC 6 cm AD x DE EC Yukarıda verilenlere göre x kaç cm dir? A) 6 B) 8 C) 10 D) 12 E) 14 ÇÖZÜM: ADC üçgeninde [AE] doğru parçası hem yükseklik hem de kenarortay olduğundan, aynı zamanda açıortaydır ve bu üçgen bir ikizkenar üçgendir. AC x olur. AF açıortayını kullanarak, x 4 8 4 x 6 3 3x 12 4x 12 x tir. Cevap : D 8) m(BAD) m(BCA) m(DAE) m(EAC) AB 15 cm 3 DE 2 BD DE x cm Yukarıda verilenlere göre, x kaç cm dir? A) 6 B) 8 C) 9 D) 12 E) 14 ÇÖZÜM: Açıortay açılarına ve dersek, ABE üçgeninin iki iç açısı olur. Yani ikizkenar bir üçgen olur. BE 15 cm dir. BD 15 x olur. 3 DE 2 BD ise 3x 2 15 x 3x 30 2x 5x 30 x 6 cm dir. Cevap : A 9) m(BCA) 90 m(BAD) 90 BD açıortay AB 15 br BC 9 br AD x www.matematikkolay.net Yukarıda verilenlere göre, x kaç br dir? A) 6 B) 7,5 C) 9 D) 10 E) 12 ÇÖZÜM: BE açıortayına göre, 9 3 15 EC 5 EC 3k, AE 5k diyebiliriz. AE ABC üçgeni ise bir 9 -12 -15 üçgenidir. 3 3k 5k 12 8k 12 k dir. 2 3 15 AE 5k 5 7,5 br dir. 2 2 Açıortay açılarına diyelim. m(BEC) olsun. 90 olur. BAD üçgeninin iç açıları toplamına göre, m(ADB) olmalıdır. İki iç açısı da olduğu için AED üçgeni ikizkenar üçgendir. x AE 7,5 br dir. Cevap : B 10) I, ABC üçgeninin iç teğet çemberinin merkezi DE // BC AB 12 cm AC 15 cm Yukarıda verilenlere göre, ADE üçgeninin çevresi kaç br dir? A) 15 B) 19 C) 22 D) 24 E) 27 ÇÖZÜM: İç teğet çemberinin merkezi, iç açıortayların kesişim noktasıdır. Bu sebeple BI ve CI birer açıortaydır. DE // BC olduğu için, şekildeki gibi ikizkenar üçgenler oluşur (İç ters açıların eşitliği). Buna gör 15 12 e, Ç(ADE) x y a b 27 br dir. Cevap : E
 Bu bölümde Üçgende Açıortay ile ilgili 18 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
Bu bölümde Üçgende Açıortay ile ilgili 18 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar… 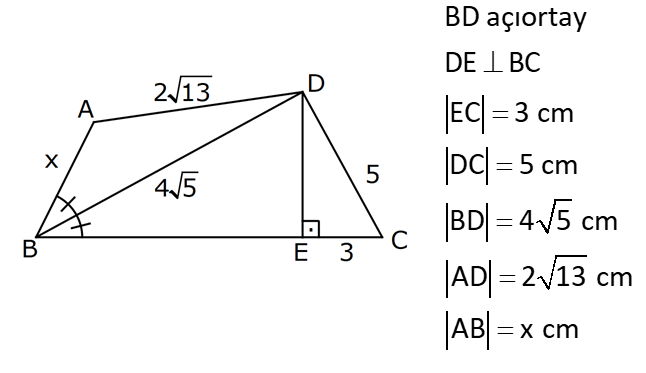
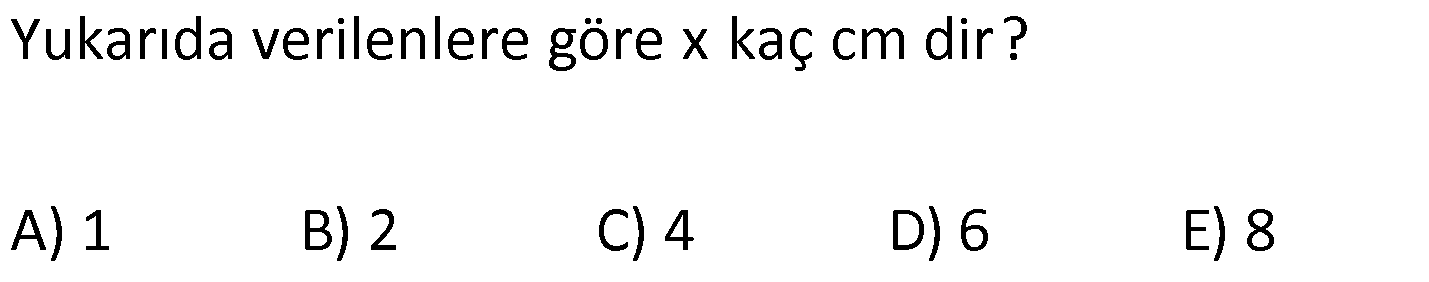

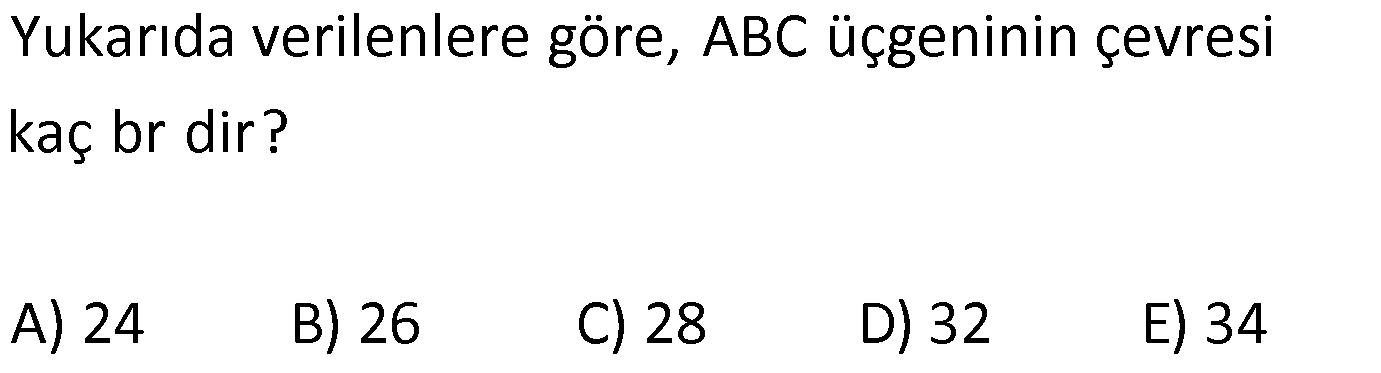

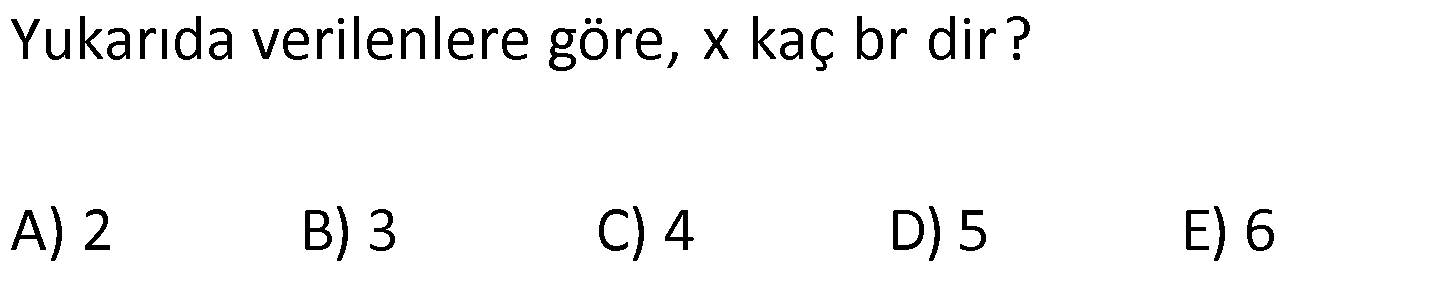

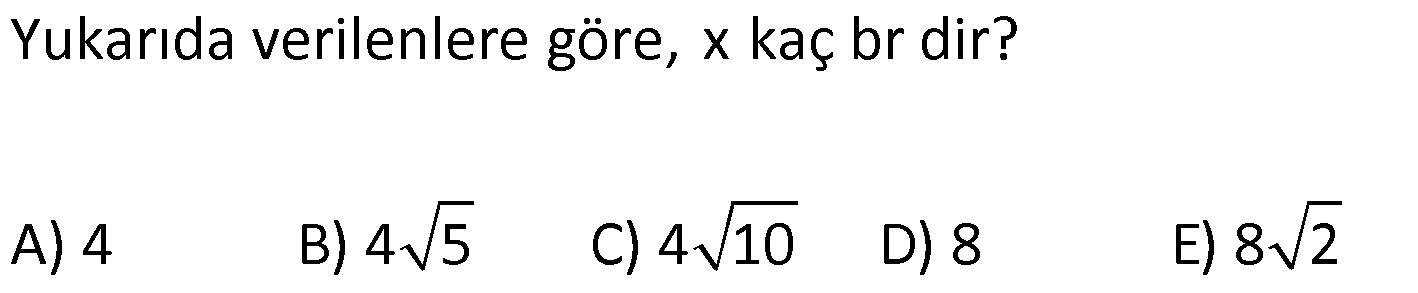

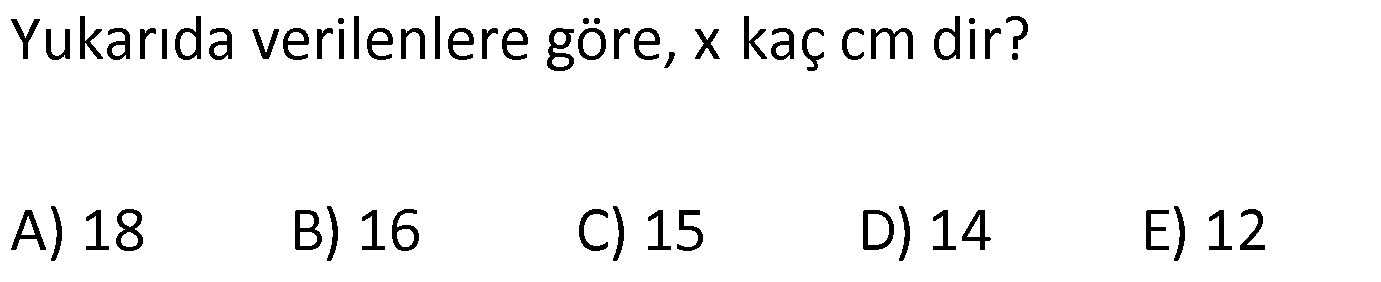


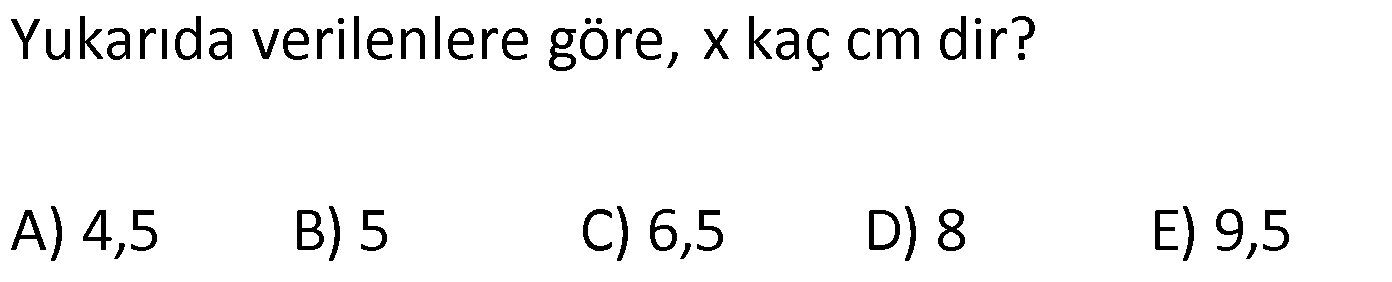
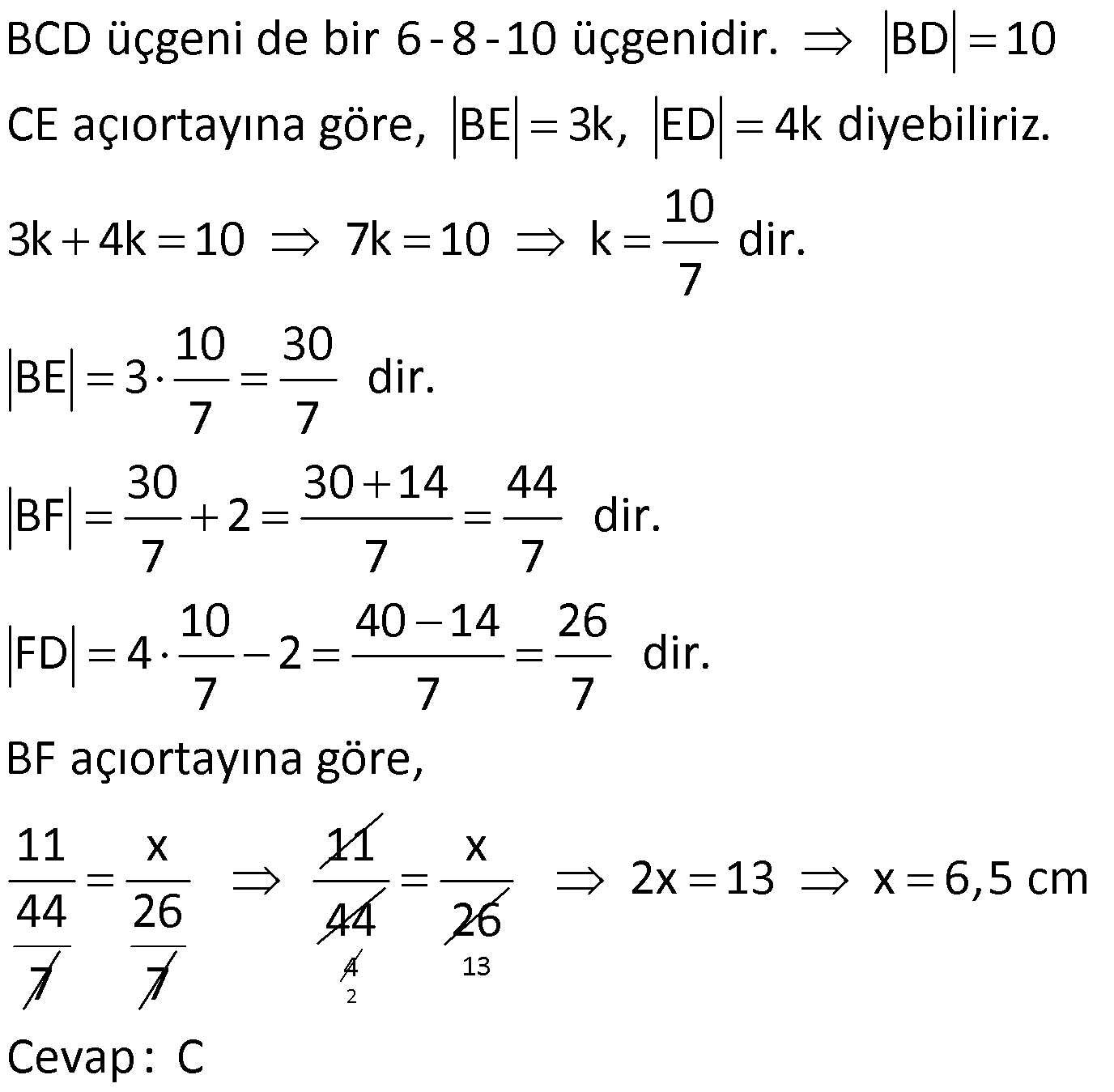
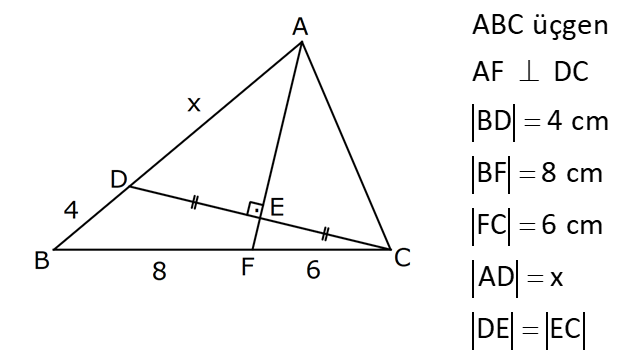
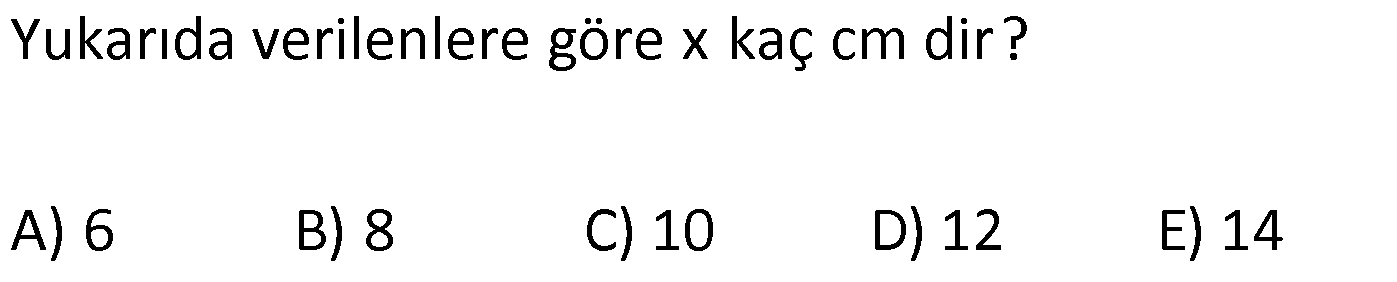
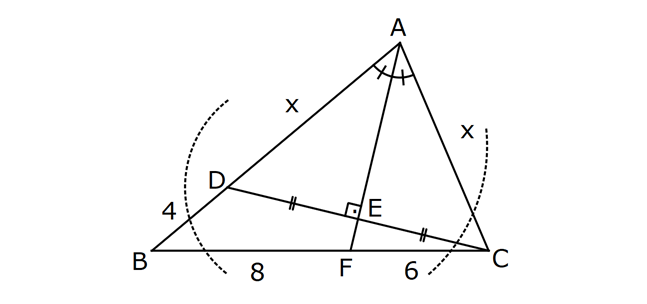


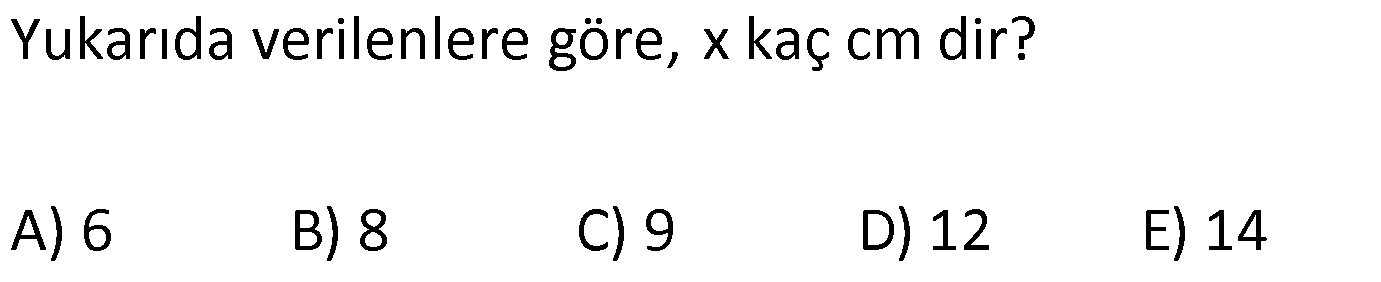


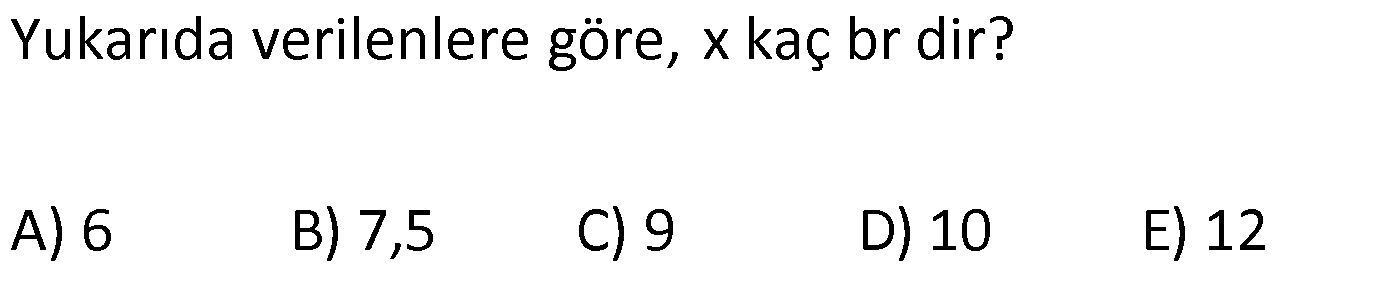

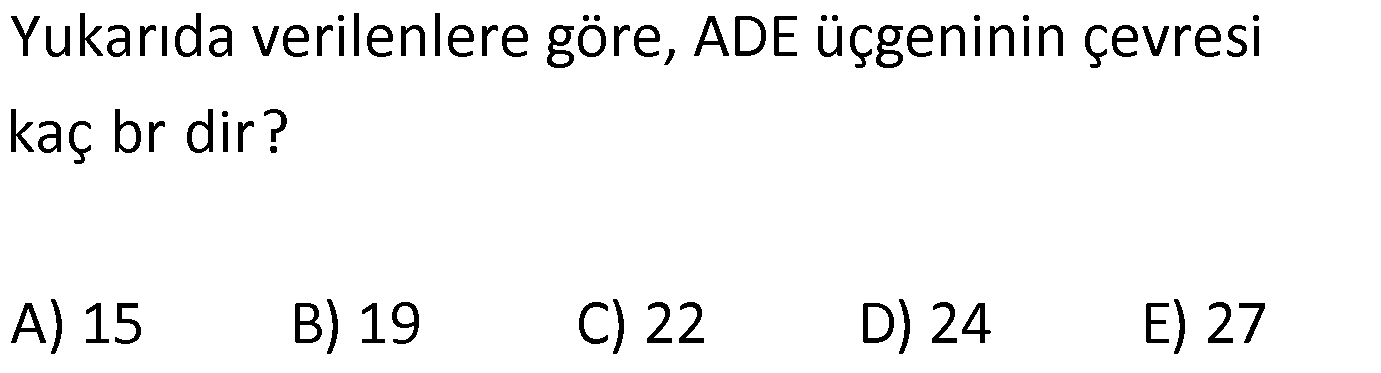



5. soru yok
Uyarınız için teşekkürler. Soru yerine yanlışlıkla çözümü gelmiş. Şimdi düzeltildi.
efsanesin başkan onnumara sorular :)))