11.SORU
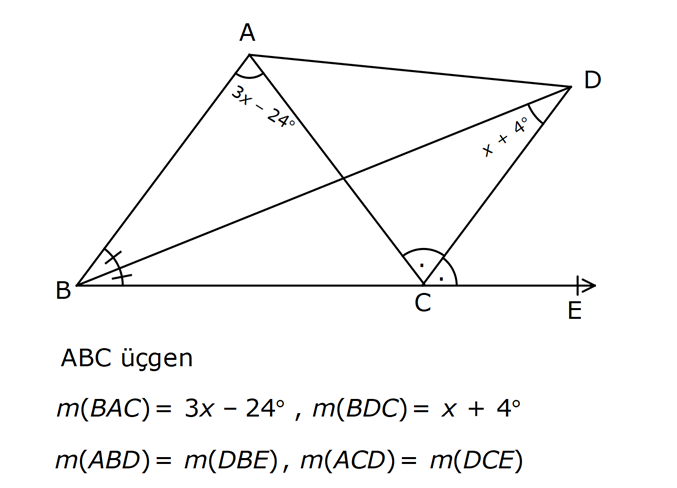
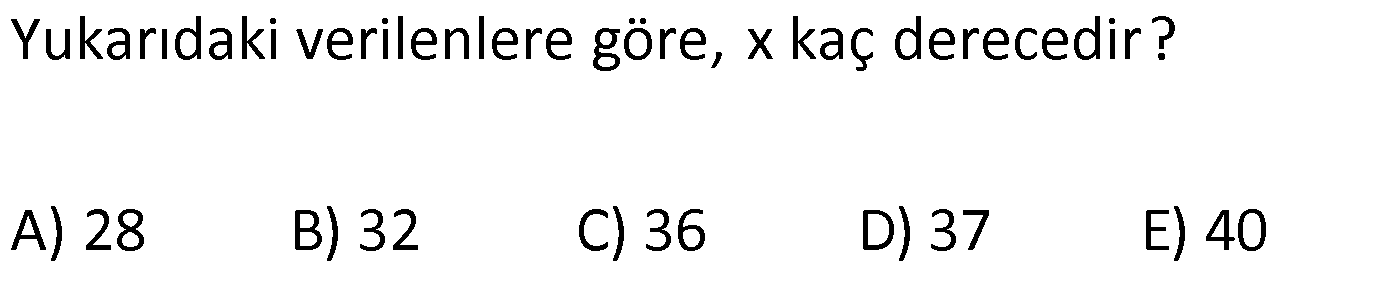
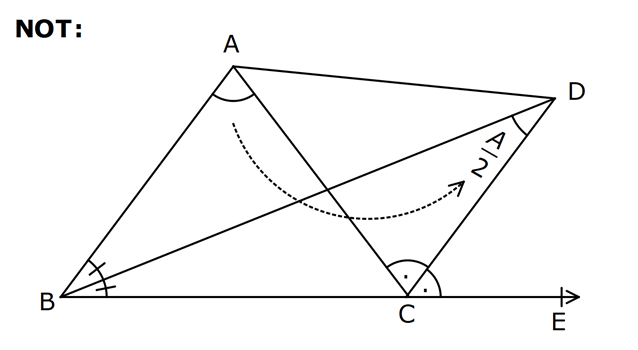
| | | | | |
Çözüm için Tıklayınız.

12.SORU
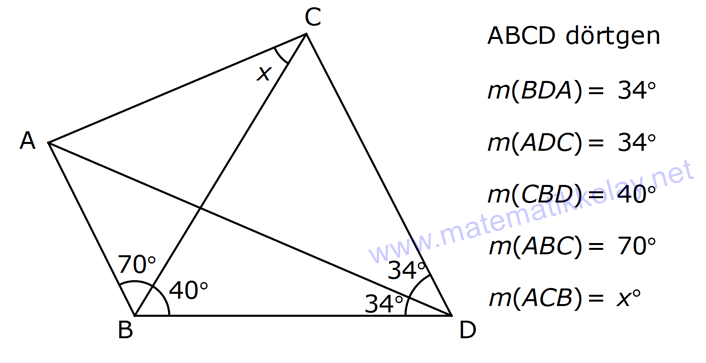
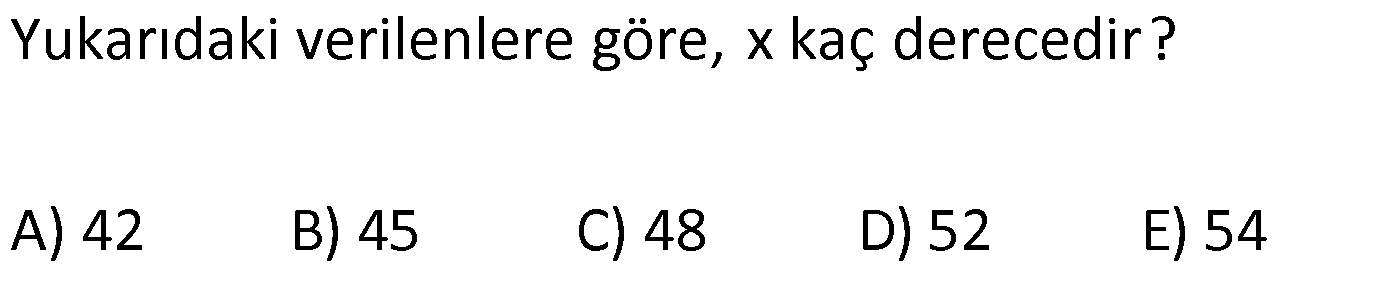
| | | | | |
Çözüm için Tıklayınız.
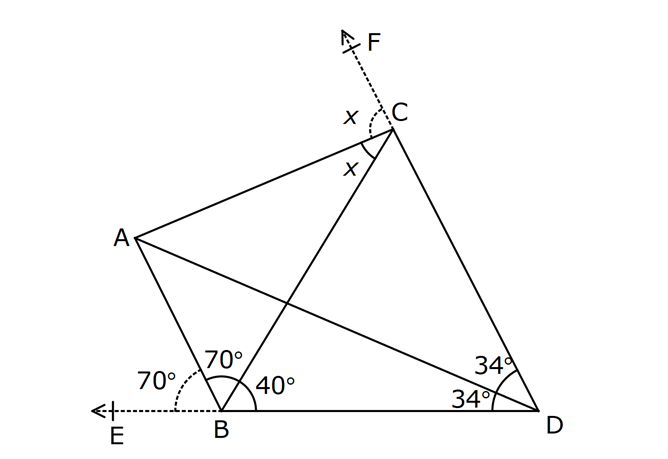

13.SORU
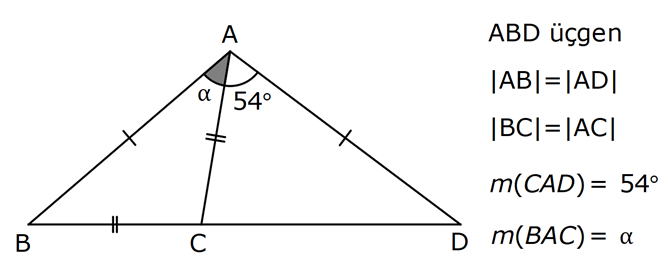
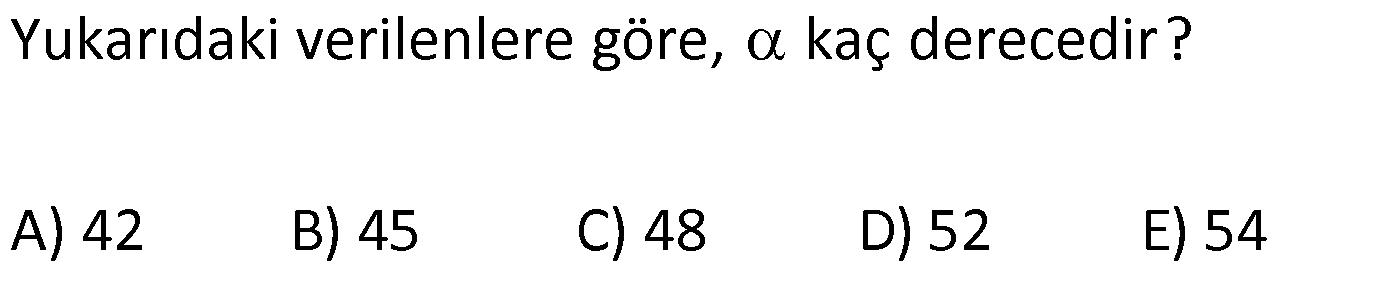
 | | | | |
Çözüm için Tıklayınız.
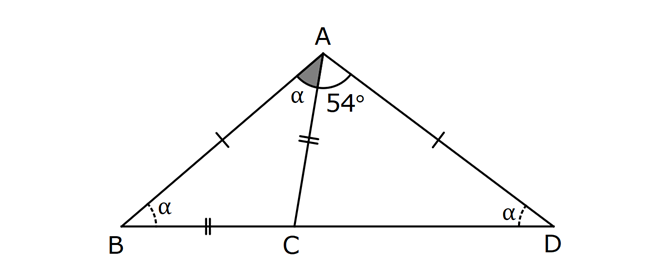

14.SORU
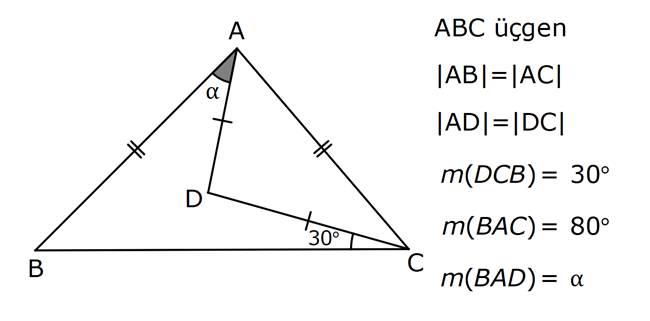
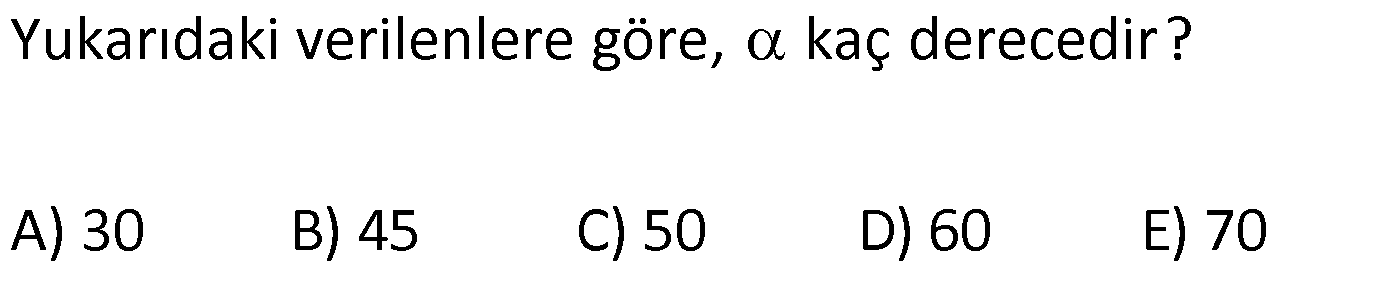
| | | | | |
Çözüm için Tıklayınız.
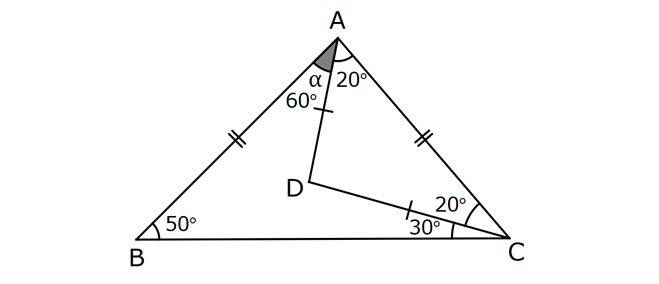

15.SORU
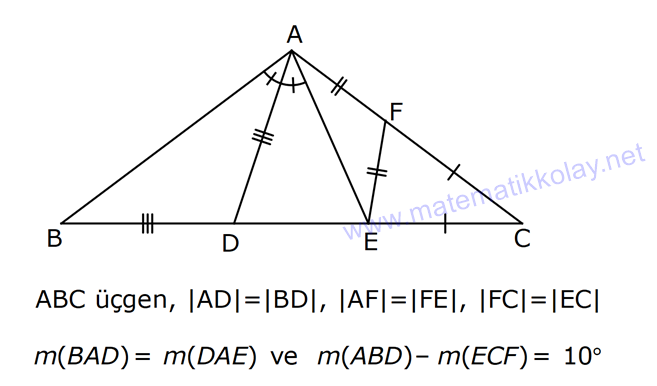
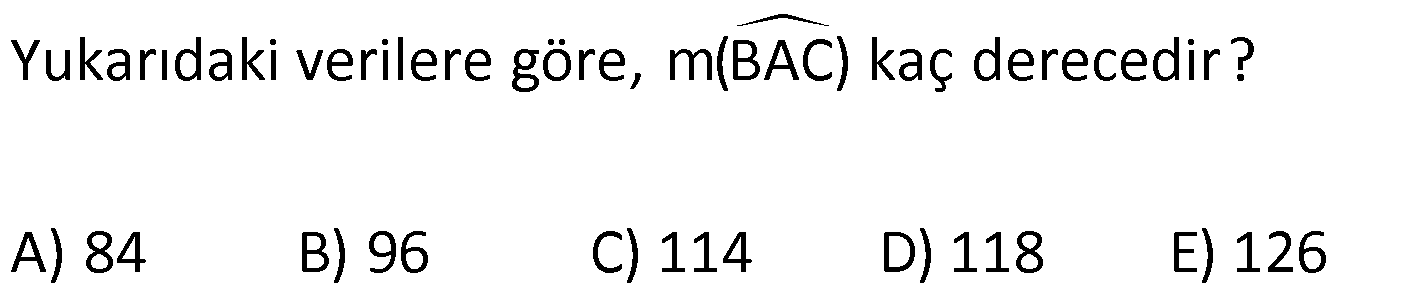
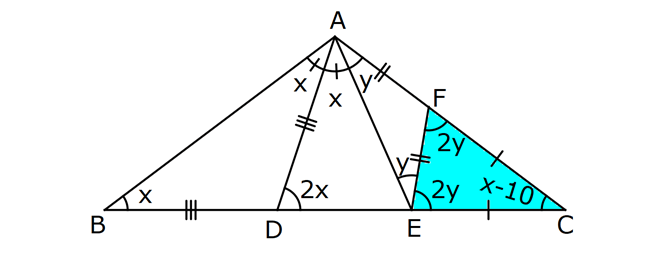
| | | | | |
Çözüm için Tıklayınız.

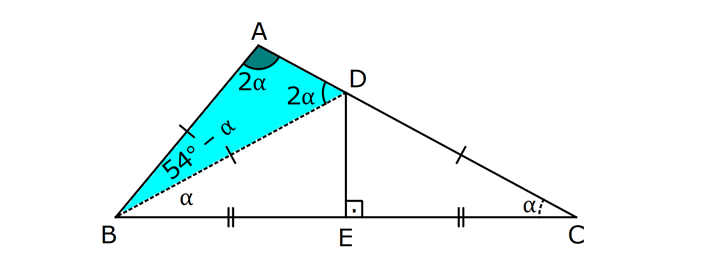
16.SORU
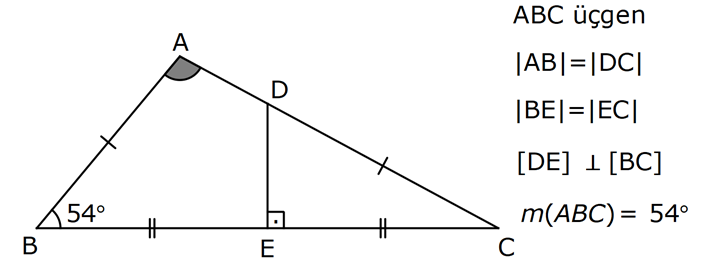
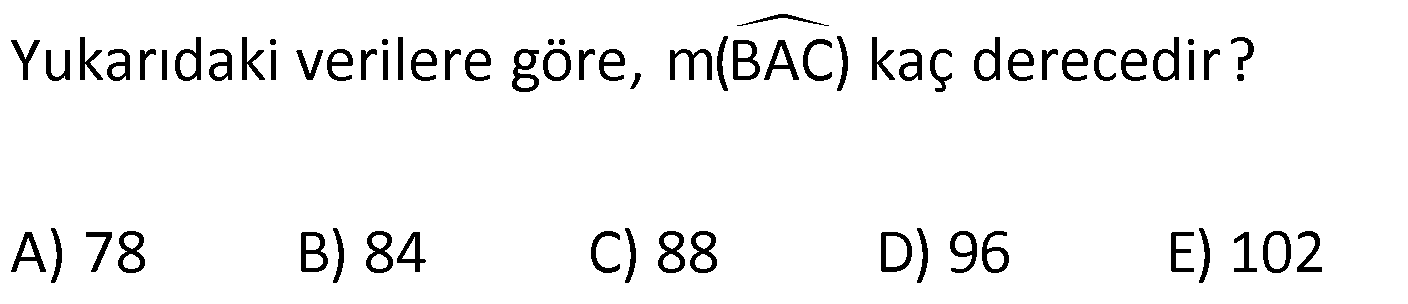
| | | | | |
Çözüm için Tıklayınız.

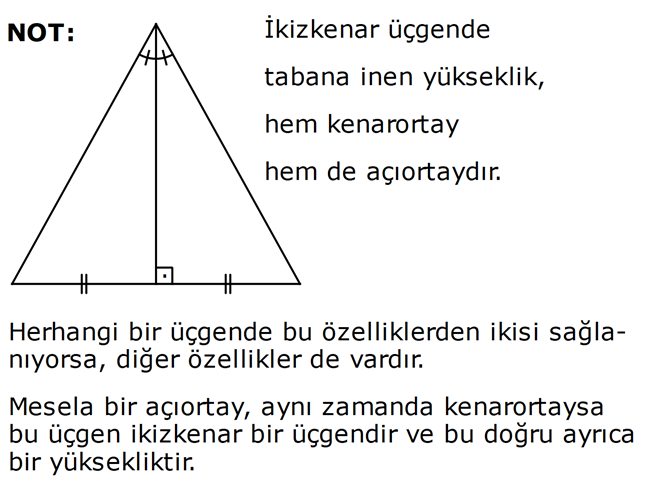
17.SORU
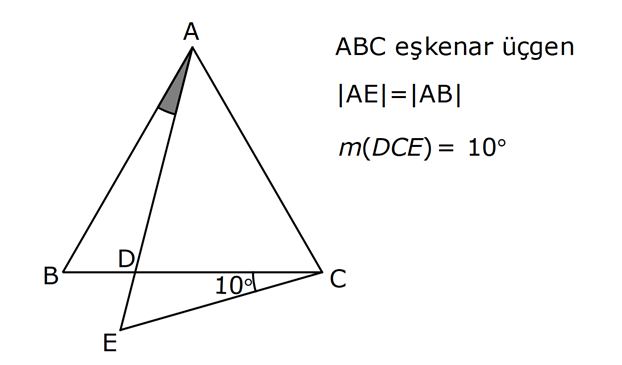
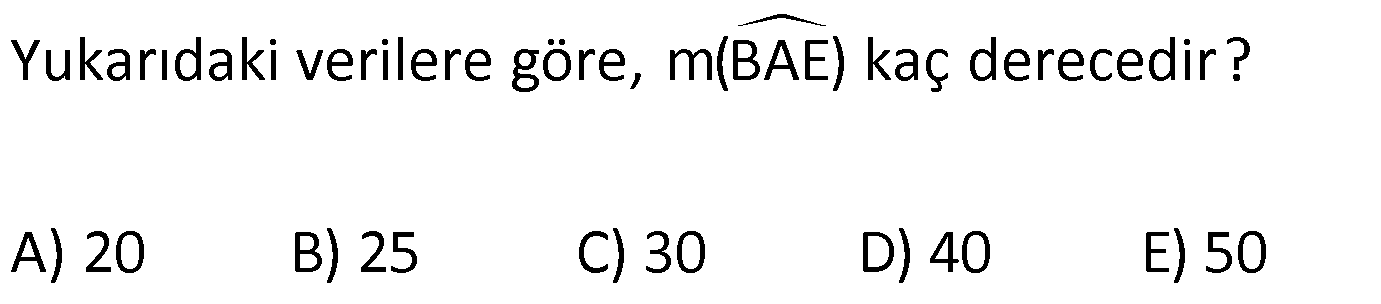
 | | | | |
Çözüm için Tıklayınız.
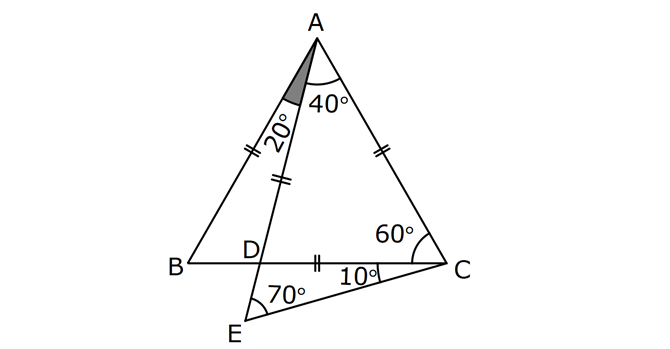

18.SORU
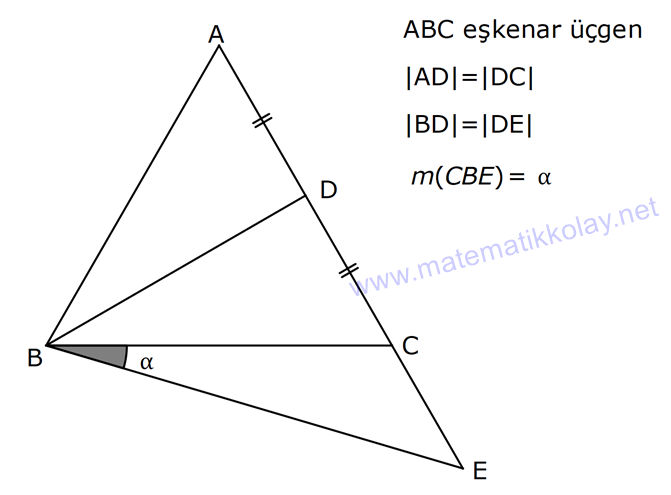
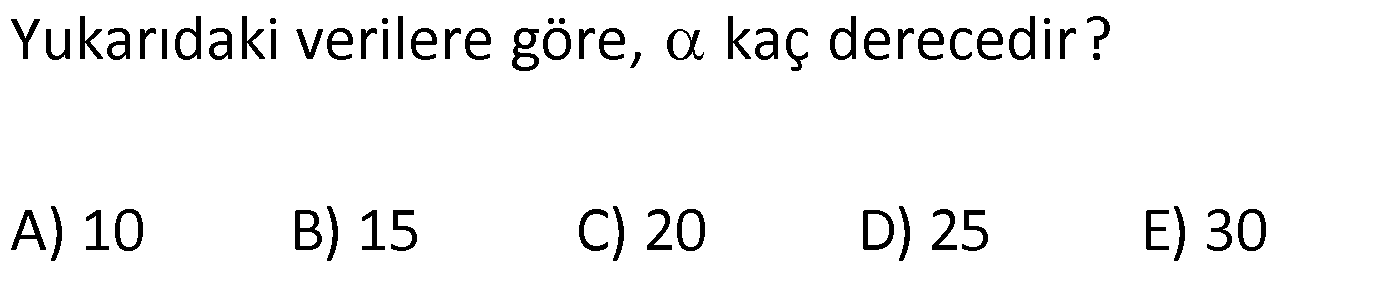
| | | | | |
Çözüm için Tıklayınız.
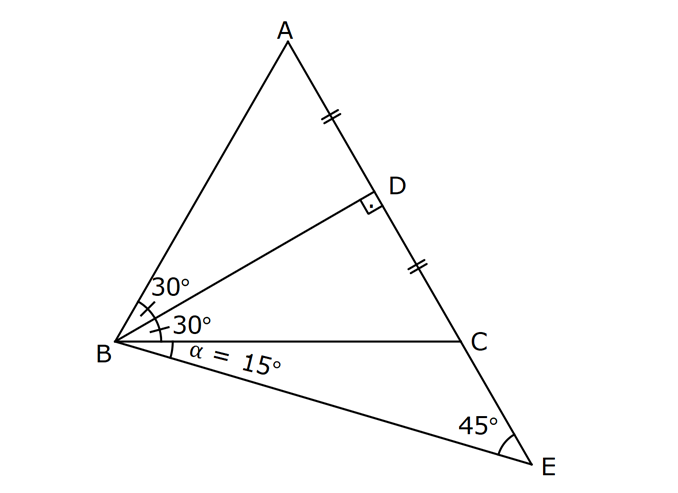

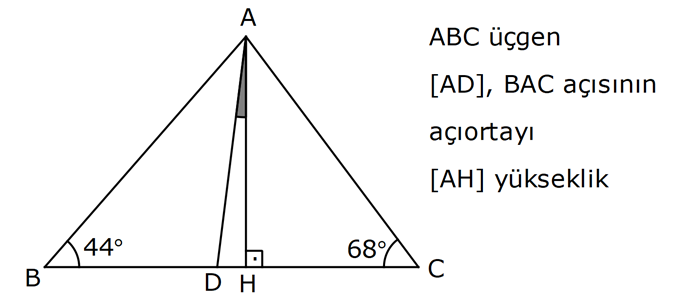
19.SORU
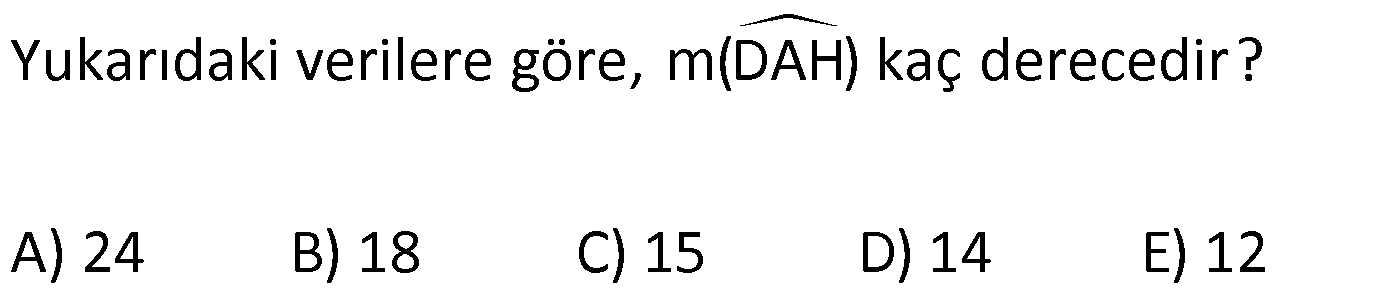
| | | | | |
Çözüm için Tıklayınız.

Sayfalar: 1 2


gayet güzel
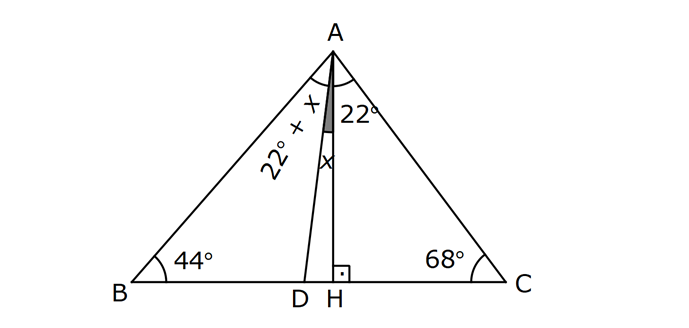
meraba, bu 90-2x-30bölü2
neden x+15 oldu x-15 olmasıgerekmez mi
– işareti içeriye dağıtıldığı için x+15 olur.
Neresi güzel ya
Vallaha Haklısn
Çok güzel sorular çok beğendim 👍
asena güzel değşlse yapama bence gayet güzel
Offffff çok zordu beynim dondu
Hayır ya hiç güzel değil bu ne
Tşkkklr sağoln işimi gördü proje odevimdi yptm
teşekkür ederim bence yeterince güzel elinize emeğinize sağlık projeme yardımcı oldunuz
sorular aşırı basit
Çok güzel
bence gayet güzel açıklanmış sorular ve yeni öğrenmeye başlayanlar için çok iyi
Eyw teşekkür ederim çok iyi sorularınız vardı 🙂
Bunkar 9. Sinif doğrumu
9.sınıf evet.
Aynı zamanda TYT ye hazırlık.
bana biraz basit geldi. ama güzel sorular ve kısa çözümler içeren sorular da var