11.SORU

| | | | | |
Çözüm için Tıklayınız.

12.SORU

 | | | | |
Çözüm için Tıklayınız.

13.SORU
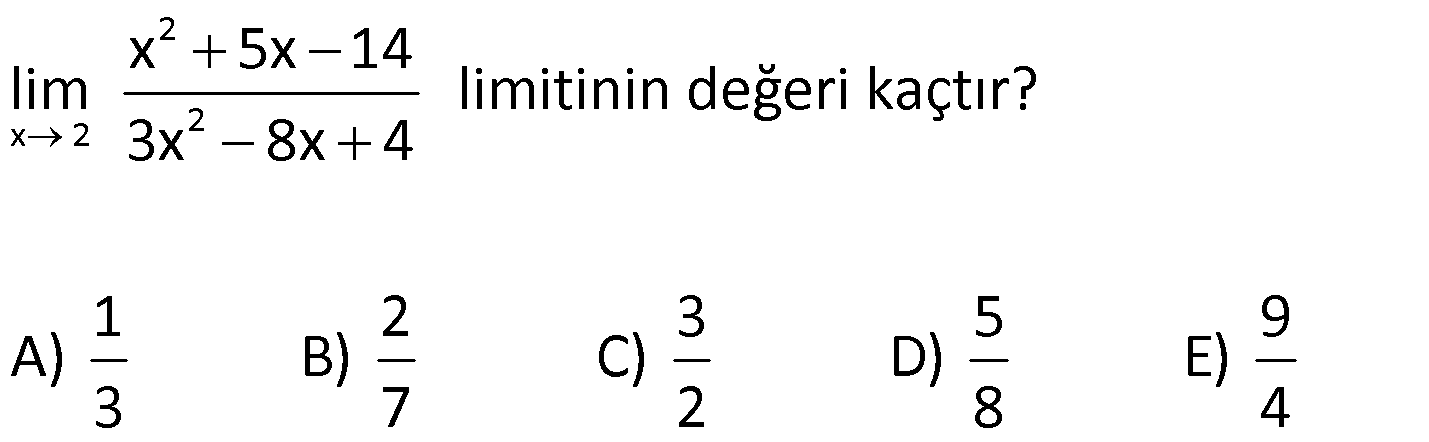
| | | | | |
Çözüm için Tıklayınız.

14.SORU

| | | | | |
Çözüm için Tıklayınız.
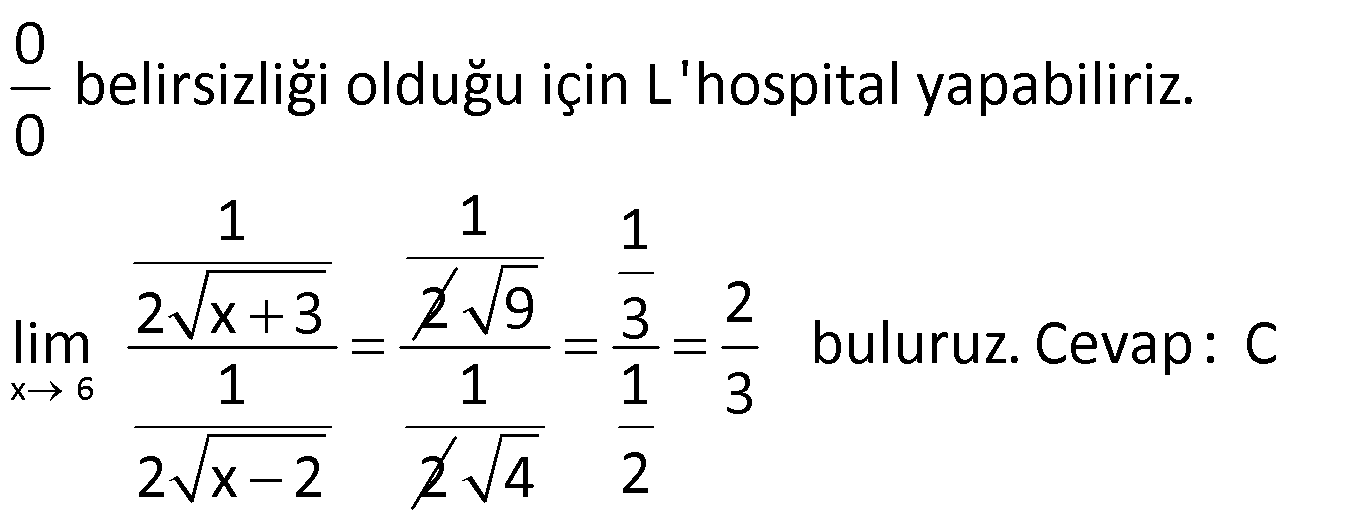
15.SORU

 | | | | |
Çözüm için Tıklayınız.

16.SORU

| | | | | |
Çözüm için Tıklayınız.
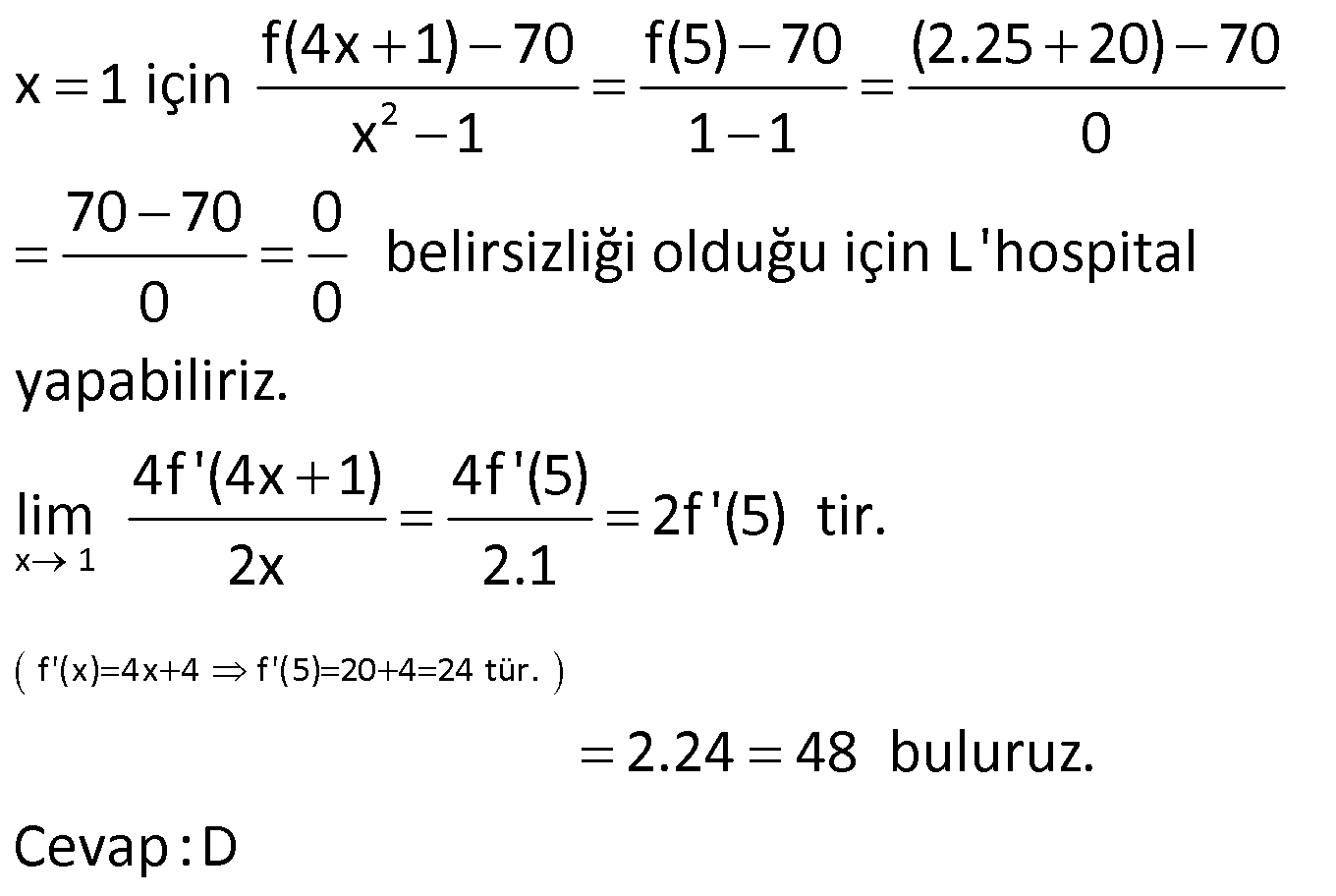
17.SORU
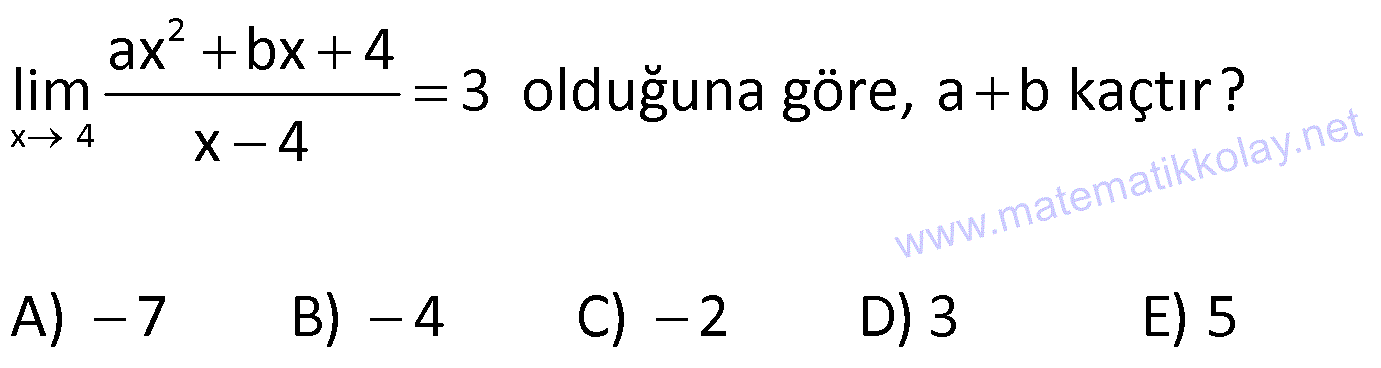
| | | | | |
Çözüm için Tıklayınız.

Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
11) 2 a bir reel sayı olmak üzere, f(x) 3x ax 3 fonksiyonu tüm reel sayılarda türevli ise, a’nın alabileceği en büyük değer için f'(a) kaçtır? A) 22 B) 26 C) 30 D) 36 E) 42 ÇÖZÜM: 2 2 2 Mutlak değerin birinci dereceden bir kökü olmazsa reel sayılarda türevli olur. Yani, çift katlı kökü olabilir ya da hiç kökü olmayabilir. O halde, 0 olmalıdır. a 4.3.3 0 a 36 0 a 36 6 a 6 aralığında 2 olmalıdır. a’nın en büyük değeri 6 dır. Mutlak değerin içi negatif olamadığı için direkt dışarı çıkar. (Başkatsayısı pozitif) f(x) 3x 6x 3 f'(x) 6x 6 olur. f'(6) 36 6 42 buluruz. Cevap : E www.matematikkolay.net 12) 2 Gerçel sayılarda tanımlı olan, ax x 2 x 2 f(x) bx x 2 x 2 fonksiyonu tüm reel sayılarda türevli ise, a b kaçtır? A) 3 B) 2 C) 1 D) 0 E) 1 ÇÖZÜM: f(x) fonksiyonu x 2 de sürekli olmalıdır. f(2 ) 2a 0 2a dır. f(2 ) 4b 0 4b dir. 2a 4b olmalı a 2b dir. Soldan ve sağdan türevler de birbirine eşit olmalıdır. x 2 için f'(x) (ax ( x 2))’ a 1 dir. x 2 2 2b idi. 1 için f'(x) (bx (x 2))’ 2bx 1 dir. f'(2 ) 4b 1 olur. a 1 4b 1 olmalıdır. a 4b 2 2b 2 b 1 dir. a 2b 2 olur. a b ( 2) ( 1) 3 buluruz. Cevap: A 13) 2 2 x 2 x 5x 14 lim limitinin değeri kaçtır? 3x 8x 4 1 2 3 5 9 A) B) C) D) E) 3 7 2 8 4 ÇÖZÜM: 0 Limit alırken belirsizliği ile karşılaşıyorsak, 0 Pay ve paydanın ayrı ayrı türevini alıp limit hesaplayabiliriz. (Bölümün türevi değil.) olarak geçen bu kural, müfredatta yer al Not : L’hospital kuralı 2 2 mıyor. Ancak bilinmesinde büyük yarar vardır. x 5x 14 4 10 14 0 x 2 için = belirsizliği 3x 8x 4 12 16 4 0 L’hospital yapalım. 2x 5 Pay ve paydanın türevini alırsak olur. 6x 8 4 5 9 x 2 yazalım. buluruz 12 8 4 2 2 x 2 x 2 . Çarpanlarına ayırarak x 5x 14 (x 7) (x 2) lim lim 3x 8x 4 II.Yol: (3x 2) (x 2) 9 9 tür. 6 2 4 Cevap: E 14) x 6 x 3 3 lim limitinin değeri kaçtır? x 2 2 3 1 2 3 4 A) B) C) D) E) 2 3 3 2 3 ÇÖZÜM: x 6 0 belirsizliği olduğu için L’hospital yapabiliriz. 0 1 1 2 x 3 2 lim 1 2 x 2 9 1 2 1 3 2 buluruz. Cevap: C 1 3 4 2 15) 3 h 4 f(x) x 2 fonksiyonu veriliyor. f(h) f(4) lim limitinin değeri kaçtır? 2x 8 A) 24 B) 32 C) 48 D) 50 E) 66 ÇÖZÜM: www.matematikkolay.net 2 h 4 4 Türevin tanımından burasının f'(4) olduğunu biliyoruz. h 4 1 f(h) f(4) 1 1 1 lim f'(4) 3x 3.16 24 tür. 2 x 4 2 2 2 0 belirsizliği olduğu için L’hospital yapabiliriz. 0 f'(h) f’ lim 2 II. Yol: L’hospital (4) 48 24 tür. Cevap: A 2 2 16) 2 2 x 1 f(x) 2x 4x fonksiyonu veriliyor. f(4x 1) 70 lim limitinin değeri kaçtır? x 1 A) 25 B) 32 C) 40 D) 48 E) 50 ÇÖZÜM: 2 x 1 f'(x) 4x 4 f'(5) 20 4 24 tür. f(4x 1) 70 f(5) 70 (2.25 20) 70 x 1 için x 1 1 1 0 70 70 0 belirsizliği olduğu için L’hospital 0 0 yapabiliriz. 4f'(4x 1) 4f'(5) lim 2f'(5) tir. 2x 2.1 2.24 48 buluruz. Cevap 😀 17) 2 x 4 ax bx 4 lim 3 olduğuna göre, a b kaçtır? x 4 A) 7 B) 4 C) 2 D) 3 E) 5 ÇÖZÜM: x 4 x 4 için payda 0 dır. 0 Bu ifadenin bir limiti varsa, belirsizliği gerçekleş – 0 miştir. Pay 0 olmalıdır. 16a 4b 4 0 16a 4b 4 4a b 1 dir. 0 belirsizliği olduğu için L’hospital uygulayabiliriz. 0 2 lim 1 ax b 3 8a b 3 tür. 1 8a b 3 _ 4a b 1 taraf tarafa çıkarırsak, 4a 4 a 1 dir. 8a b 3 8 b 3 b 5 tir. Buna göre, a b 1 ( 5) 4 buluruz. Cevap : B

