11.SORU
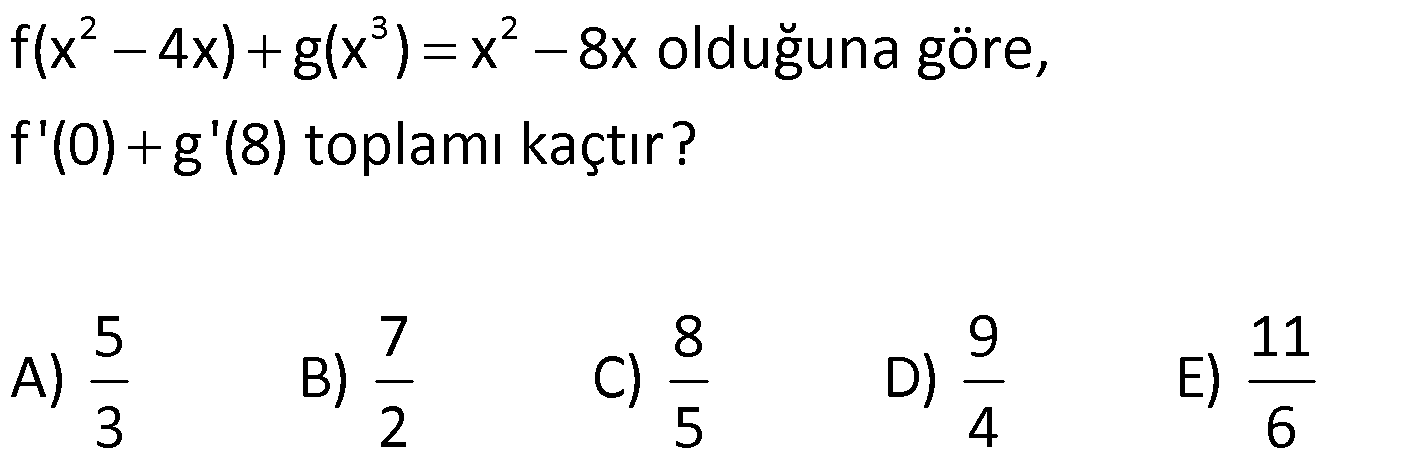
 | | | | |
Çözüm için Tıklayınız.

12.SORU

| | | | | |
Çözüm için Tıklayınız.
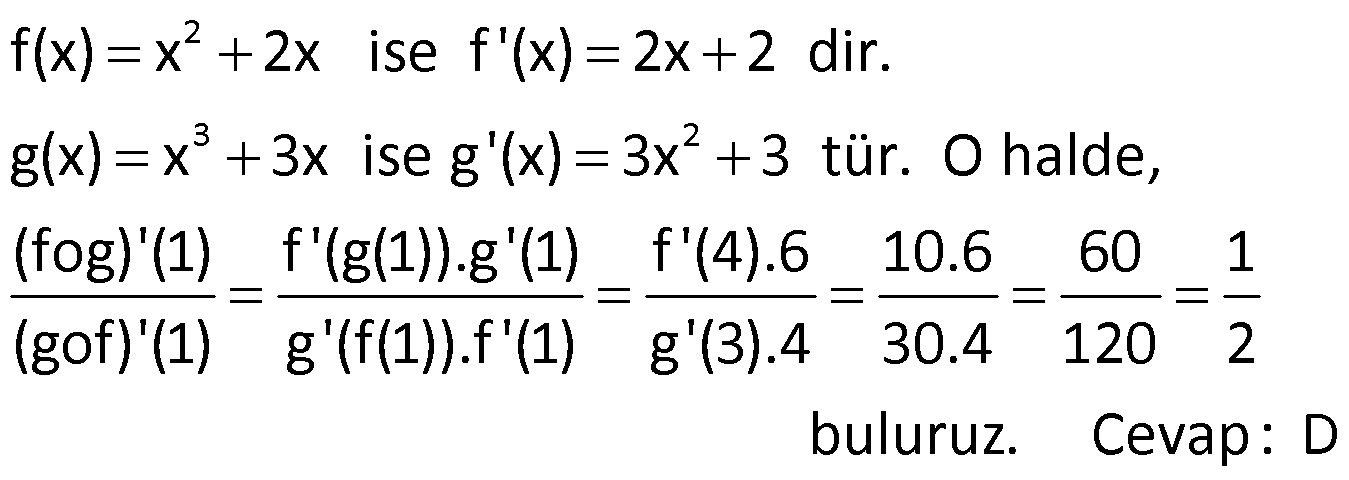
13.SORU
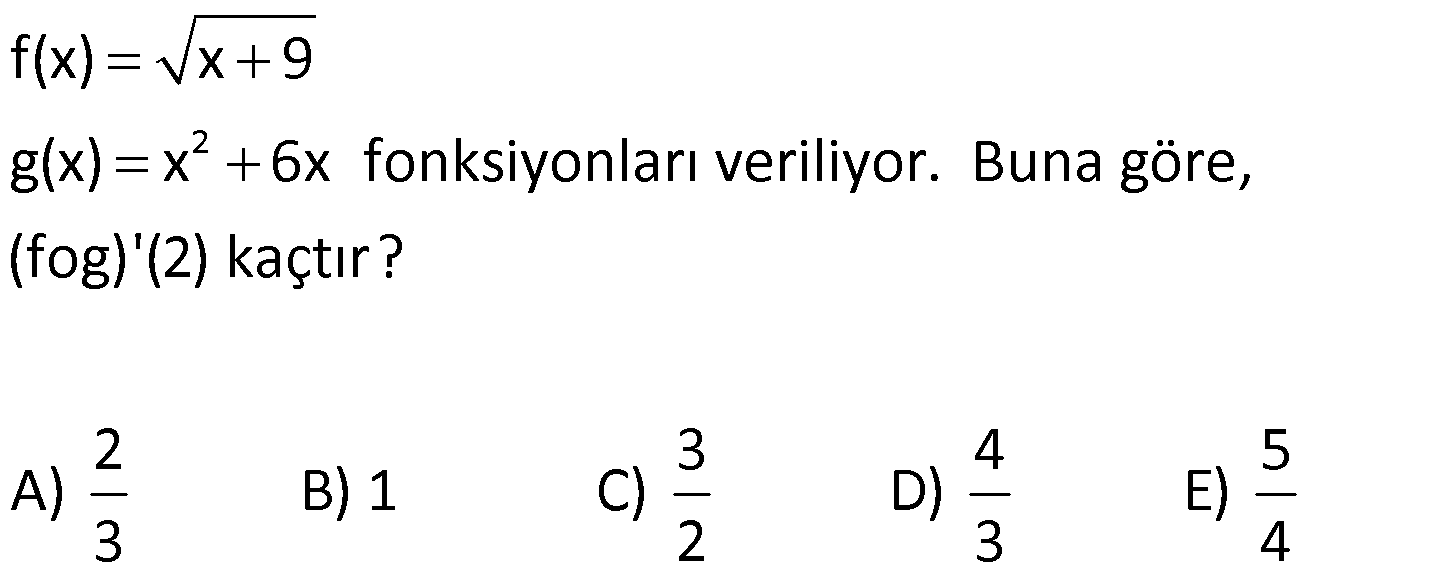
| | | | | |
Çözüm için Tıklayınız.

14.SORU

| | | | | |
Çözüm için Tıklayınız.

15.SORU

| | | | | |
Çözüm için Tıklayınız.
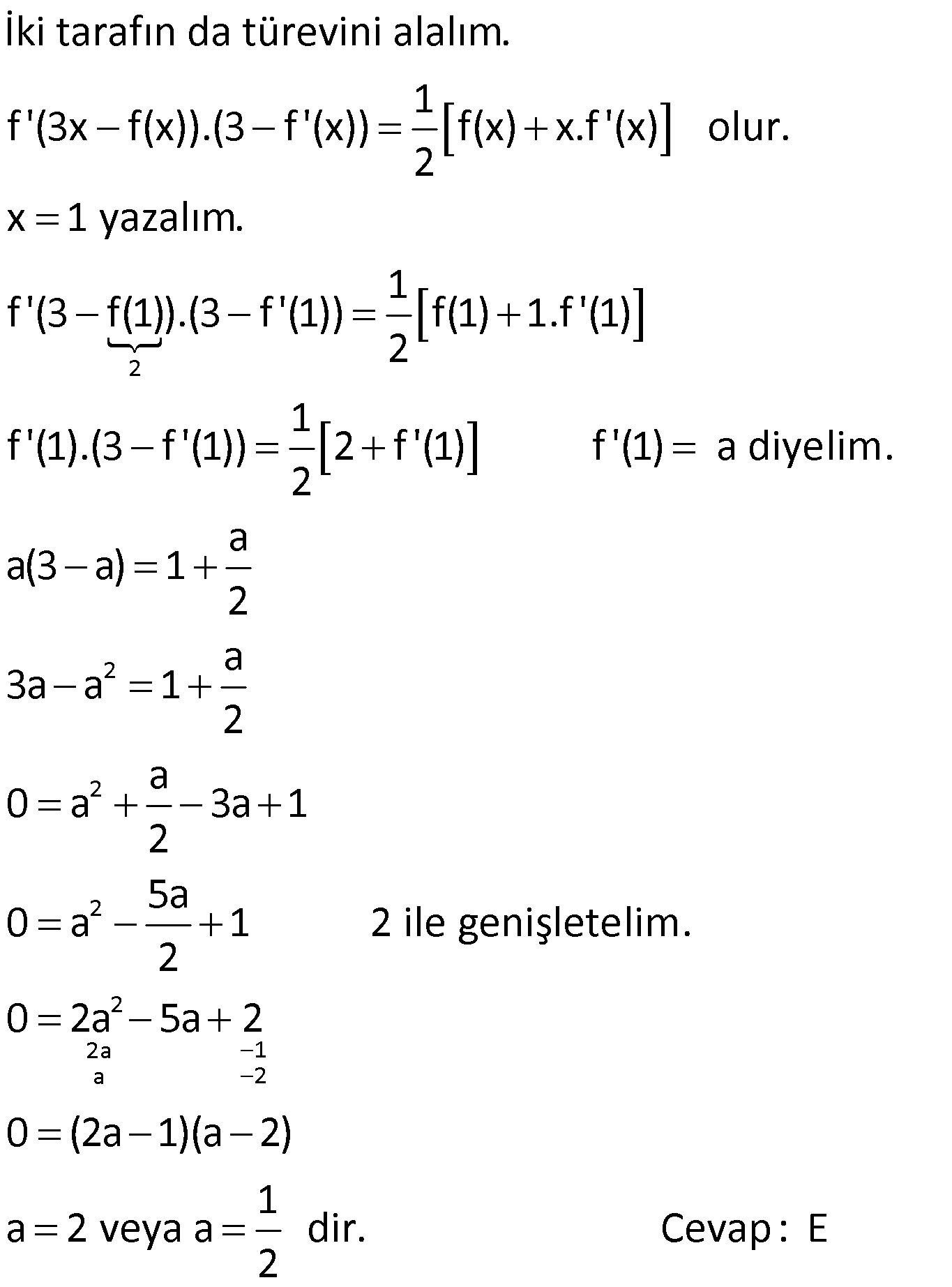
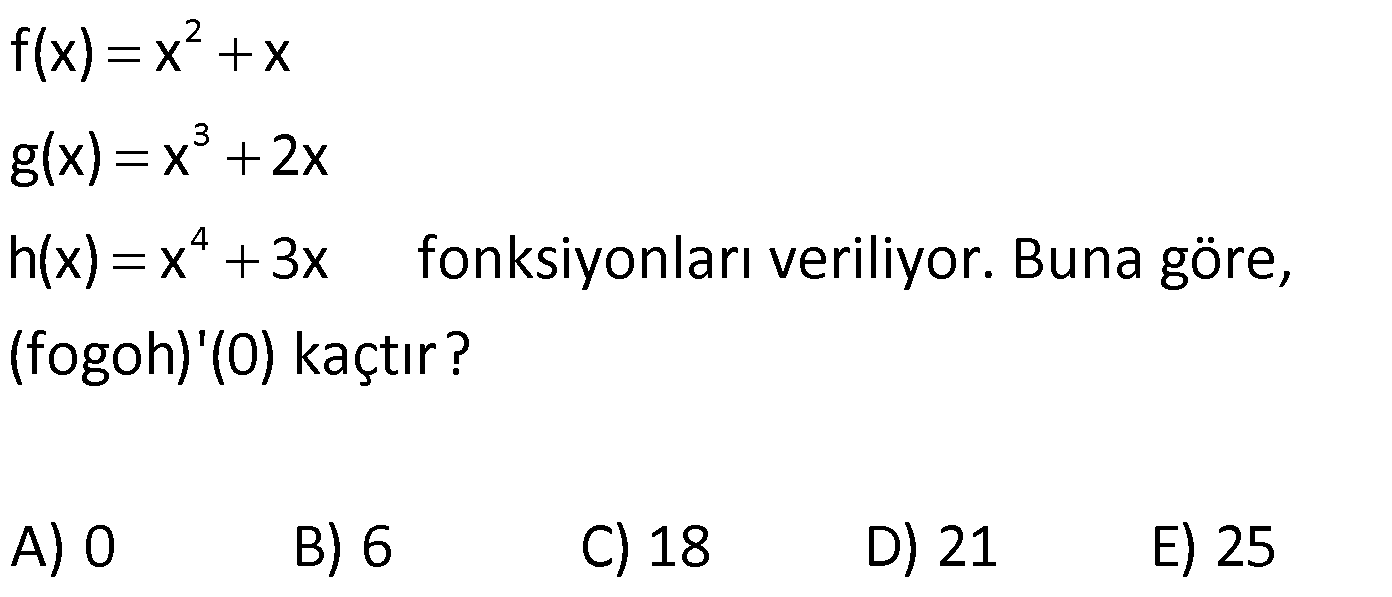
16.SORU
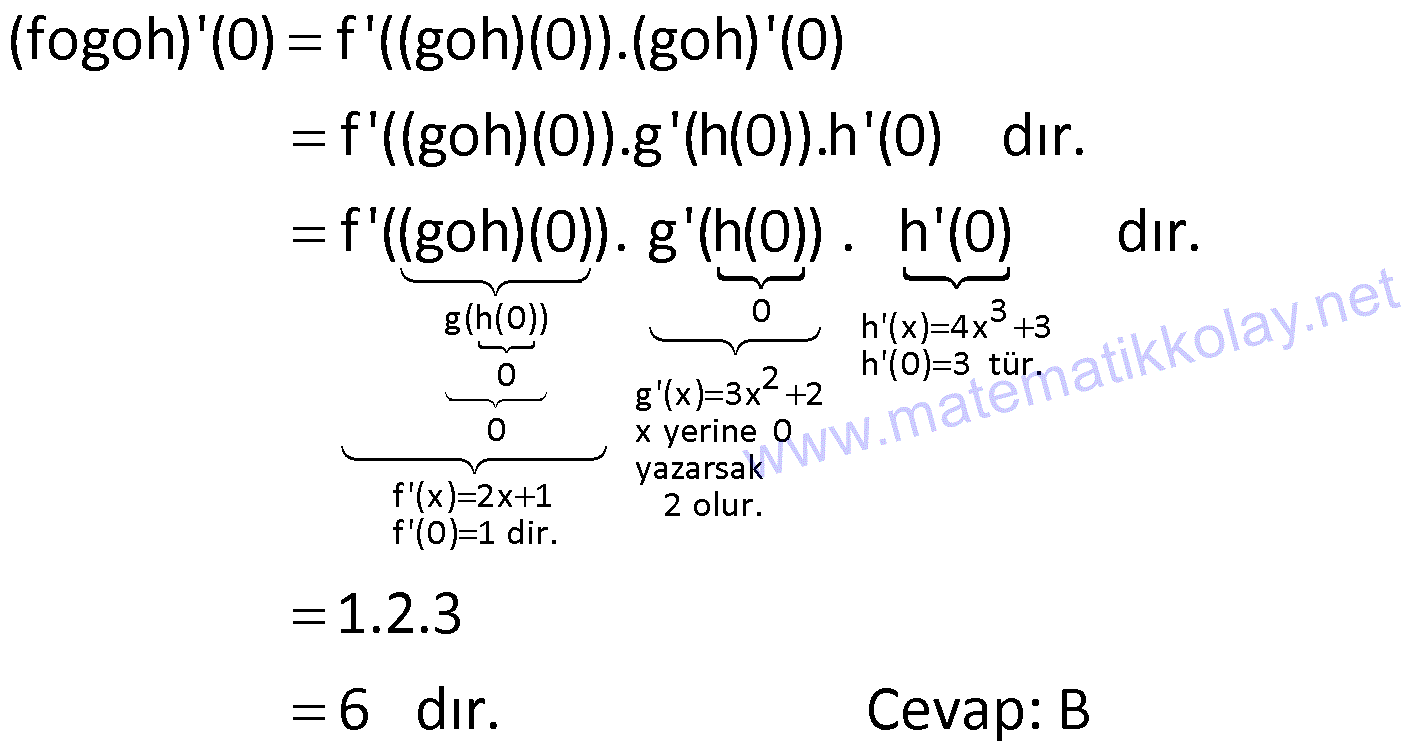
| | | | | |
Çözüm için Tıklayınız.
17.SORU
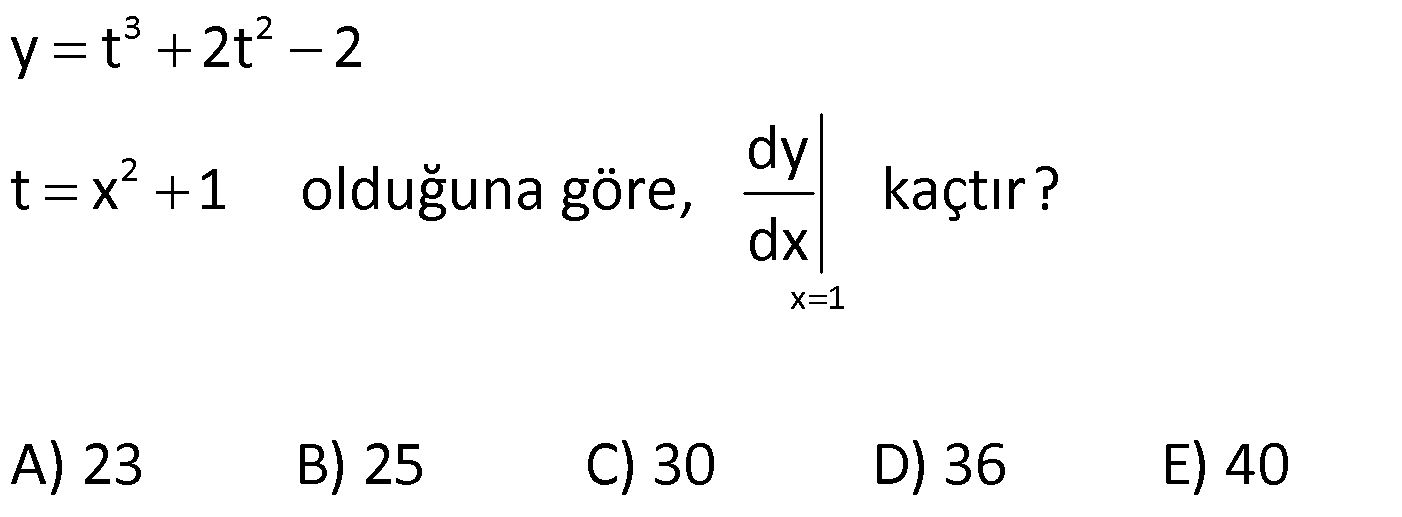
| | | | | |
Çözüm için Tıklayınız.

18.SORU
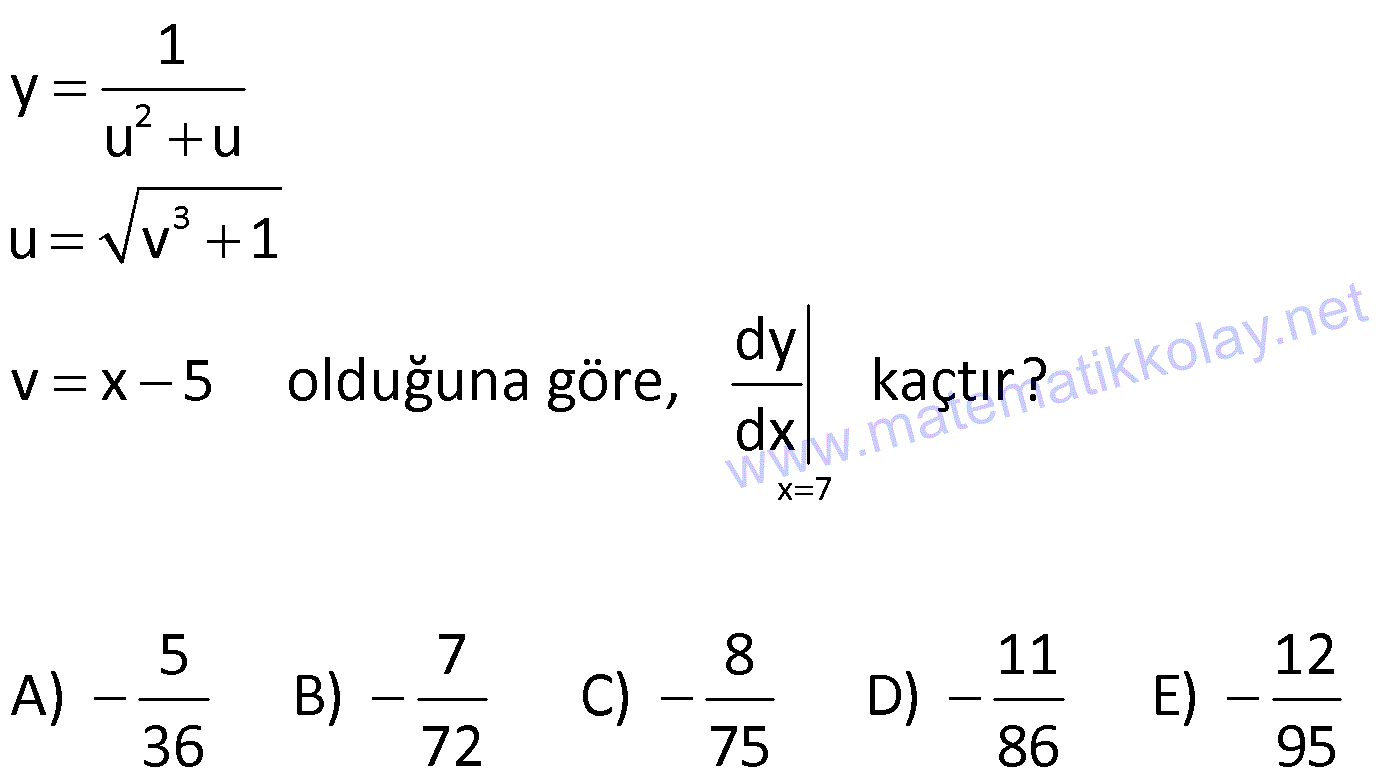
| | | | | |
Çözüm için Tıklayınız.
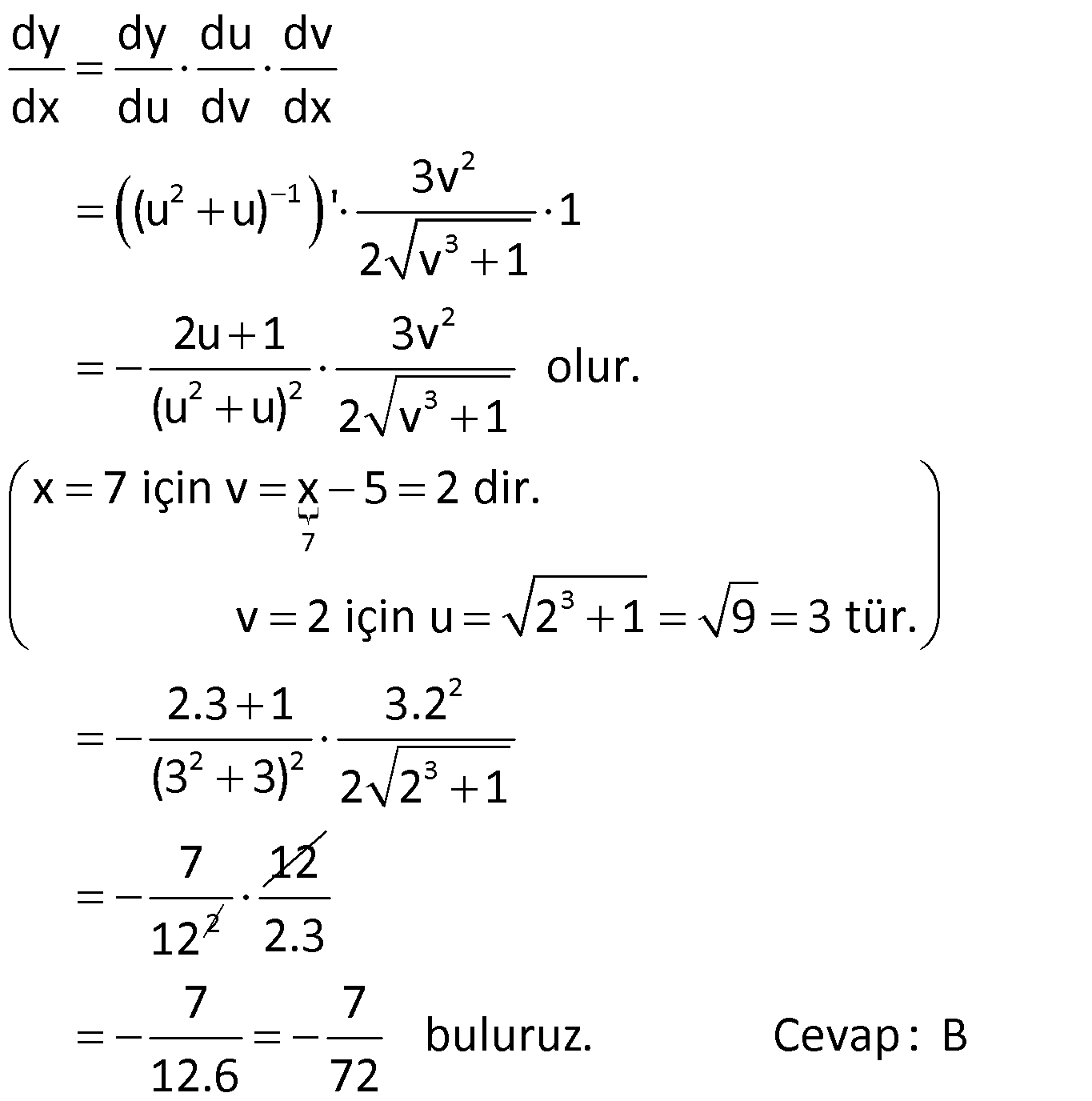
19.SORU
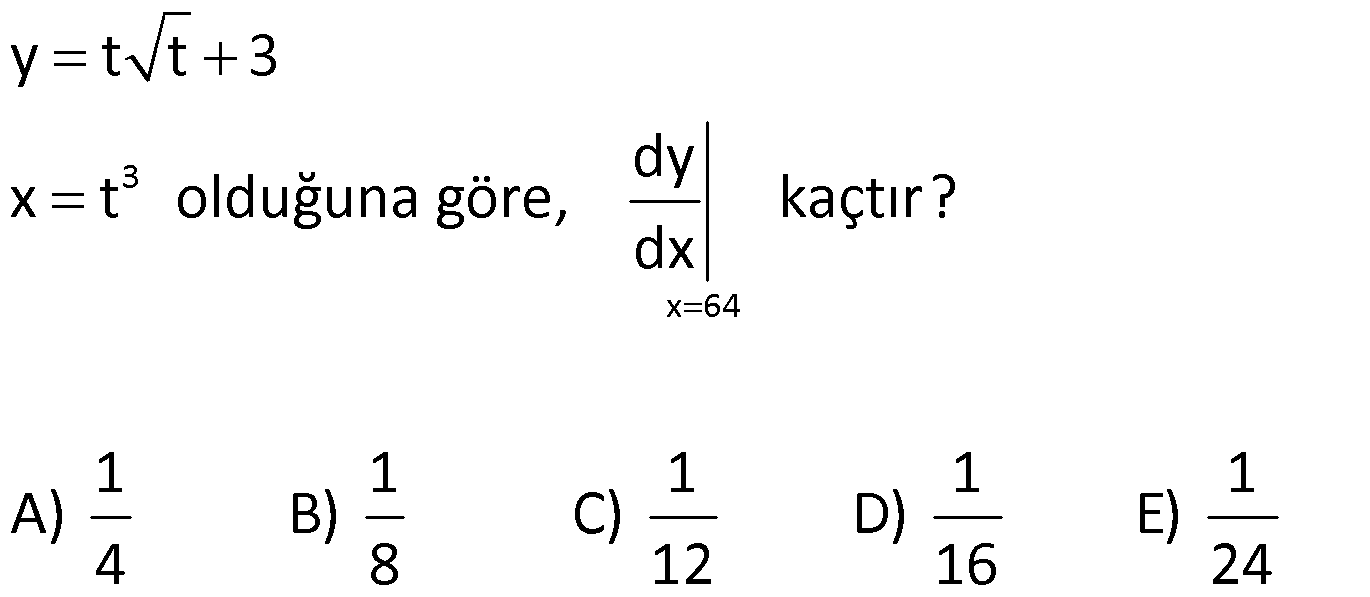
| | | | | |
Çözüm için Tıklayınız.

20.SORU
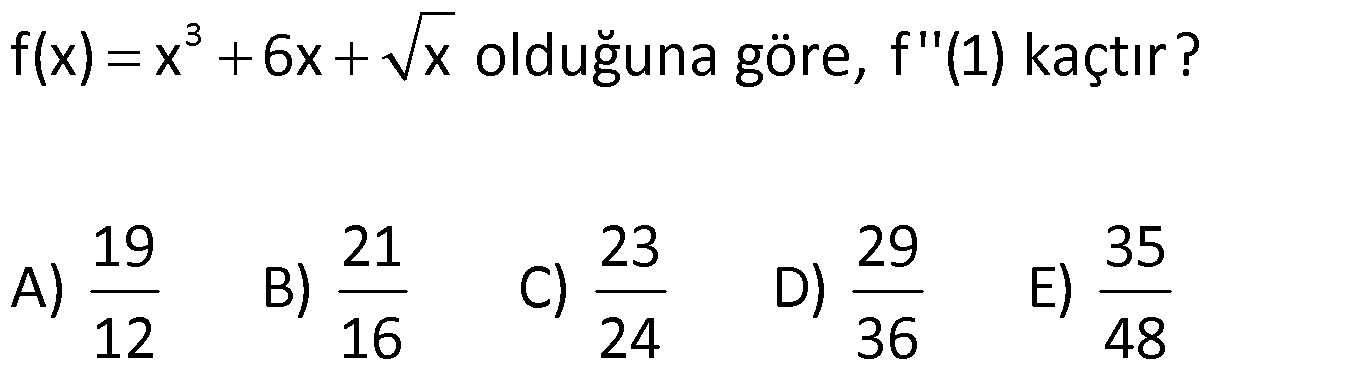
| | | | | |
Çözüm için Tıklayınız.

Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
11) www.matematikkolay.net 2 3 2 f(x 4x) g(x ) x 8x olduğuna göre, f'(0) g'(8) toplamı kaçtır? 5 7 8 9 11 A) B) C) D) E) 3 2 5 4 6 ÇÖZÜM: 2 3 2 2 3 2 2 f(x 4x) g(x ) x 8x türev alalım. f'(x 4x).(2x 4) g'(x ).3x 2x 8 olur. x 0 yazalım. f'(0).( 4) g'(0).0 0 8 f'(0).( 4) 8 f'(0) 2 dir. Türev eşitliğini tekrar yazalım. f'(x 4x).(2x 4 3 2 0 ) g'(x ).3x 2x 8 Bu sefer x 2 yazalım. f'(4 8).(4 4) g'(8).3.4 4 8 g'(8).12 4 1 g'(8) tür. Buna göre, 3 1 5 f'(0) g'(8) 2 tür. Cevap : A 3 3 12) 2 3 f(x) x 2x g(x) x 3x fonksiyonları veriliyor. Buna göre, (fog)'(1) oranı kaçtır? (gof)'(1) 5 3 1 1 2 A) B) C) D) E) 2 4 3 2 3 ÇÖZÜM: 2 3 2 f(x) x 2x ise f'(x) 2x 2 dir. g(x) x 3x ise g'(x) 3x 3 tür. O halde, (fog)'(1) f'(g(1)).g'(1) f'(4).6 10.6 60 1 (gof)'(1) g'(f(1)).f'(1) g'(3).4 30.4 120 2 buluruz. Cevap: D 13) 2 f(x) x 9 g(x) x 6x fonksiyonları veriliyor. Buna göre, (fog)'(2) kaçtır? 2 3 4 5 A) B) 1 C) D) E) 3 2 3 4 ÇÖZÜM: 2 2 2 Bileşke fonksiyonu elde etmek daha kolaysa, ilk önce bileşke fonksiyonu elde edip, sonra türev alabiliriz. (fog)(x) f(g(x)) f(x 6x) x 6x 9 (x 3) x 3 tür. (x 2 için, içer 2 isi pozitiftir. Bu sebeple, direkt x 3 yazabildik.) x 3 ün de türevi 1 dir. Dolayısıyla (fog)'(2) 1 olur. Cevap : B 1 f(x) x 9 ise f'(x) dur. 2 x 9 g(x) x 6x ise g'(x) 2x 6 dır. O h II.Yol: alde, (fog)'(2) f'(g(2)).g'(2) f’ 4 12 (2.2 6) 1 1 10 10 1 dir. 2 16 9 2.5 14) 2 1 1 2 f 1 fonksiyonu veriliyor. Buna göre, x x x f'(4) kaçtır? A) 3 B) 5 C) 8 D) 9 E) 11 ÇÖZÜM: www.matematikkolay.net 2 2 2 2 u olsun. u 1 dir. Fonksiyonun kendisini elde etmek daha kolay. İki tarafın türevini alarak başlamayalım. 1 2 1 1 in karesi 1 dir. Yani, x x x 1 1 2 f 1 fonksiyonu f(u) u 1 x x x olarak 2 2 3 2 yazabiliriz. f(x) x 1 ise f'(x) 2x tir. f'(4) 8 olur. İki tarafın da türevini alalım. 1 1 2 2 f’ 1 olur. x x x x f’ nin içini 4 yapan II.Yol: 1 x değeri tür. 3 1 2 2 f’ 4 1 1 1 9 27 9 f'(4).9 54 18 f'(4).9 72 f'(4) 8 dir. Cevap : C 15) x.f(x) f(3x f(x)) eşitliği veriliyor. 2 f(1) 2 ise f'(1) kaç olabilir? 1 3 5 A) B) 1 C) D) E) 2 3 2 3 ÇÖZÜM: 2 2 İki tarafın da türevini alalım. 1 f'(3x f(x)).(3 f'(x)) f(x) x.f'(x) olur. 2 x 1 yazalım. 1 f'(3 f(1)).(3 f'(1)) f(1) 1.f'(1) 2 1 f'(1).(3 f'(1)) 2 f'(1) f'(1) a diyelim. 2 a a(3 a) 1 2 3a a 1 2 2 2 2 a 1 a 2 a 2 a 0 a 3a 1 2 5a 0 a 1 2 ile genişletelim. 2 0 2a 5a 2 0 (2a 1)(a 2) 1 a 2 veya a dir. Cevap : E 2 16) 2 3 4 f(x) x x g(x) x 2x h(x) x 3x fonksiyonları veriliyor. Buna göre, (fogoh)'(0) kaçtır? A) 0 B) 6 C) 18 D) 21 E) 25 ÇÖZÜM: g(h(0)) 0 0 2 g'(x) 3x 2 0 x yerine 0 y f'(x) 2x 1 f'(0) 1 dir. (fogoh)'(0) f'((goh)(0)).(goh)'(0) f'((goh)(0)).g'(h(0)).h'(0) dır. f'((goh)(0)). g'(h(0)) 3 h'(x) 4x 3 h'(0) 3 tür. azarsak 2 olur. . h'(0) dır. 1.2.3 6 dır. Cevap: B www.matematikkolay.net 17) 3 2 2 x 1 y t 2t 2 dy t x 1 olduğuna göre, kaçtır? dx A) 23 B) 25 C) 30 D) 36 E) 40 ÇÖZÜM: y f(u), u g(t) ve t h(x) olsun. dy dy du dt olarak bulabiliriz. dx du dt dx Buna göre, y nin x’e göre türevini bulmak için, zincirleme türev alabiliriz. dy d Not : Türevde Zincir Kuralı 2 2 1 2 dy dt x dt dx (3t 4t).(2x) tir. x 1 için t x 1 2 olur. x 1 ve t 2 değerlerini yazalım. (3.2 4.2).(2.1) (12 8).2 20.2 40 buluruz. Cevap:E 18) 2 3 x 7 1 y u u u v 1 dy v x 5 olduğuna göre, kaçtır? dx 5 7 8 11 12 A) B) C) D) E) 36 72 75 86 95 ÇÖZÜM: 2 2 1 3 2 2 2 3 7 3 2 2 2 3 dy dy du dv dx du dv dx 3v (u u) ‘ 1 2 v 1 2u 1 3v olur. (u u) 2 v 1 x 7 için v x 5 2 dir. v 2 için u 2 1 9 3 tür. 2.3 1 3.2 (3 3) 2 2 1 7 2 12 12 2.Mar 7 7 buluruz. Cevap : B 12.6 72 19) 3 x 64 y t t 3 dy x t olduğuna göre, kaçtır? dx 1 1 1 1 1 A) B) C) D) E) 4 8 12 16 24 ÇÖZÜM: www.matematikkolay.net 3 2 3 2 y ve x , t ye göre tanımlanmış. Bunun için dy dy dt yapabiliriz. dx dx dt t 3 ‘ 3 t t 3 ‘ t ‘ 3t 1 2 t 2 3 2 2 3 4 1 t 1 olur. t 2t 2t t x 64 olması için t 64 t 4 olmalıdır. 1 1 1 1 t 4 yazalım. dır. 2t t 2.4 4 2.4.2 16 Cevap: D y ve x arasındak II. Yol : 3 3 i bağlantıyı direkt yazabiliriz. x t ifadesinin karekökü t t t dir. y ise t t ye 3 eklenerek elde edilmiş. O halde, y x 3 yazabiliriz. 1 1 1 1 y’ tir. x 64 için olur. 2 x 2 64 2.8 16 20) 3 f(x) x 6x x olduğuna göre, f”(1) kaçtır? 19 21 23 29 35 A) B) C) D) E) 12 16 24 36 48 ÇÖZÜM: 2 2 Bir fonksiyonun türevinin bir daha türevini alırsak ikinci mertebeden türevini almış oluruz. d (f(x)) Bu durum y”, f”(x) veya olarak gösterilir. dx Buna göre, f(x) in 2 ke Not : İkinci Mertebeden Türev 1 3 2 1 2 2 3 2 3 re türevini alacağız. f(x) x 6x x 1 f'(x) 3x 6 x 2 1 1 f”(x) 6x 0 x dir. 2 2 1 6x olur. 4 x 1 1 23 x 1 yazarsak 6 6 tür. 4 1 4 4 Cevap: C

