Bu bölümde Toplam Sembolü ve Fibonacci ile ilgili 8 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
1.SORU
 |  |  |  |  |
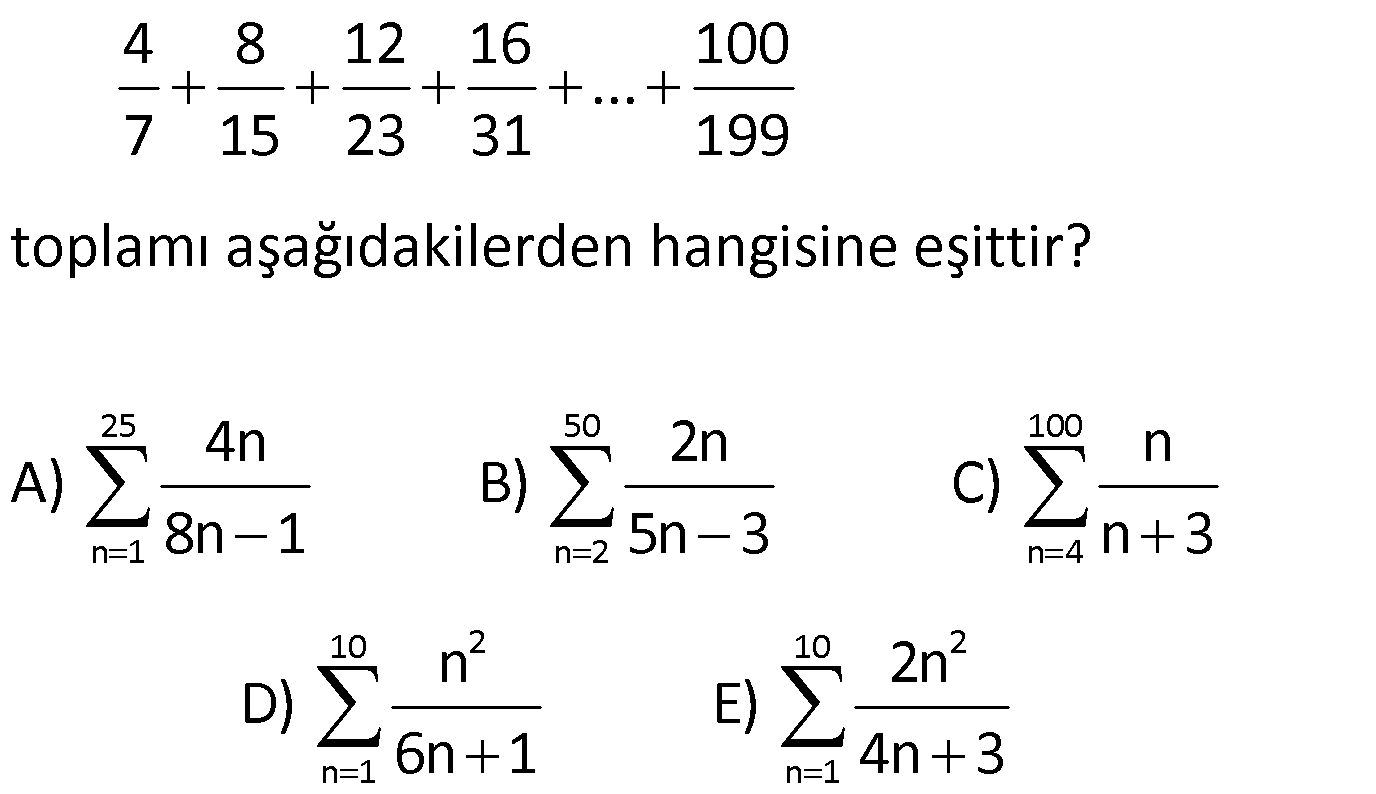
Çözüm için Tıklayınız.
2.SORU
| | | | | |
Çözüm için Tıklayınız.
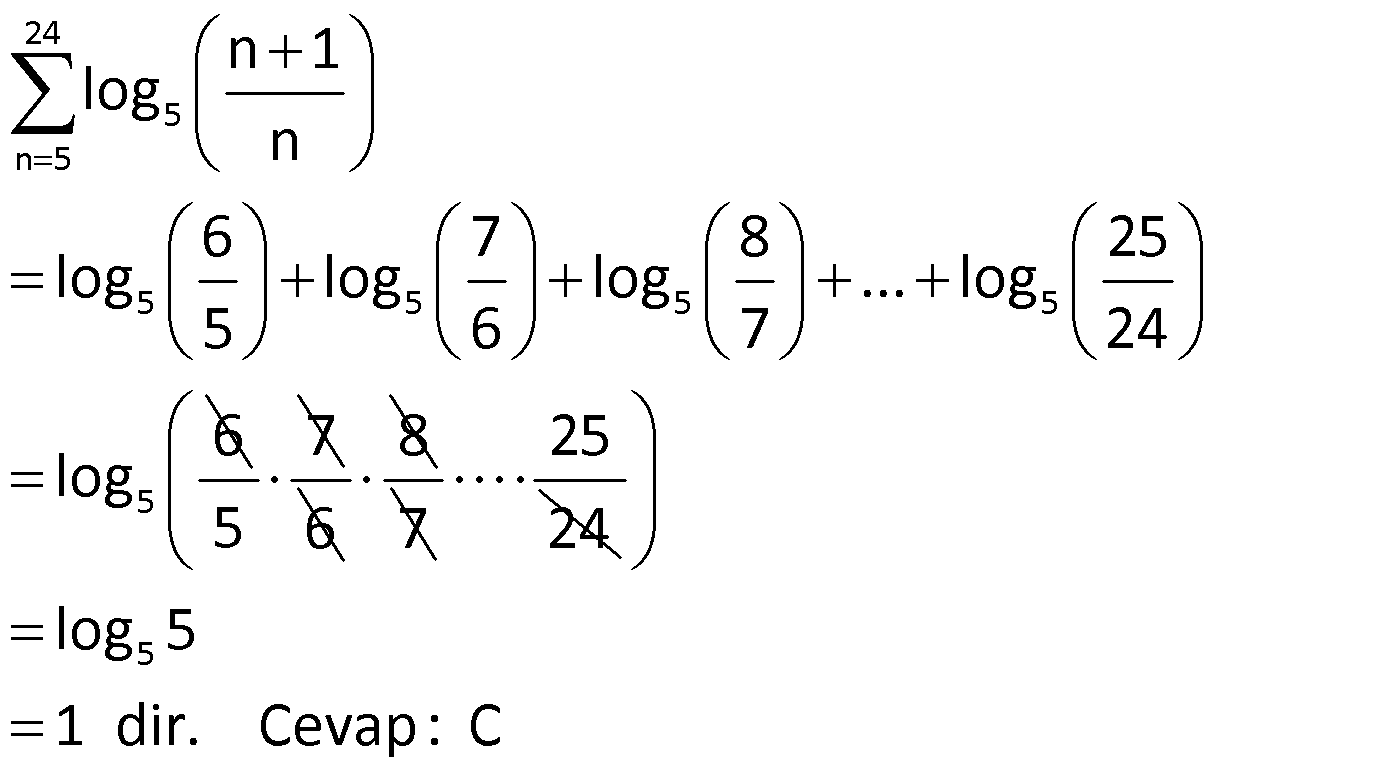
3.SORU
| | | | | |
Çözüm için Tıklayınız.
4.SORU
| | | | | |
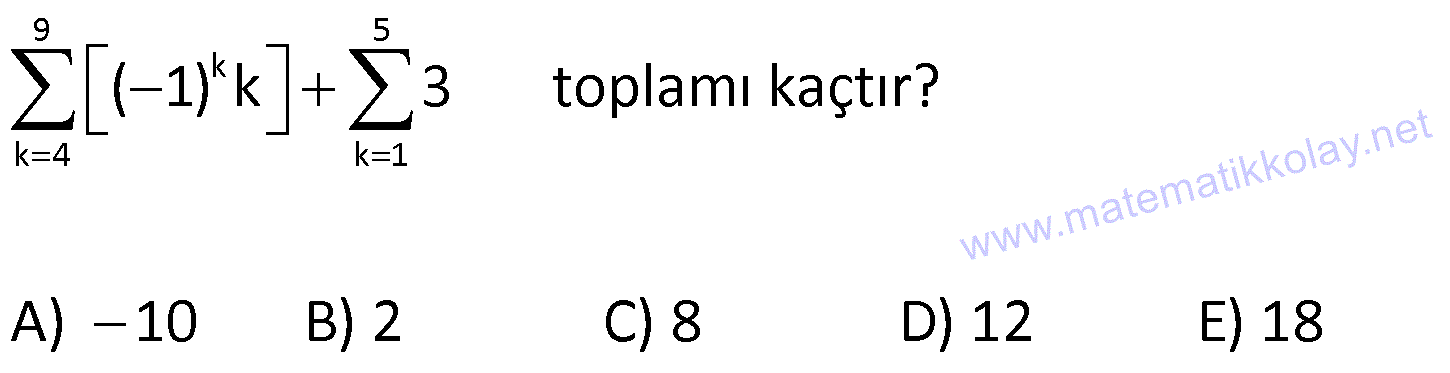
Çözüm için Tıklayınız.
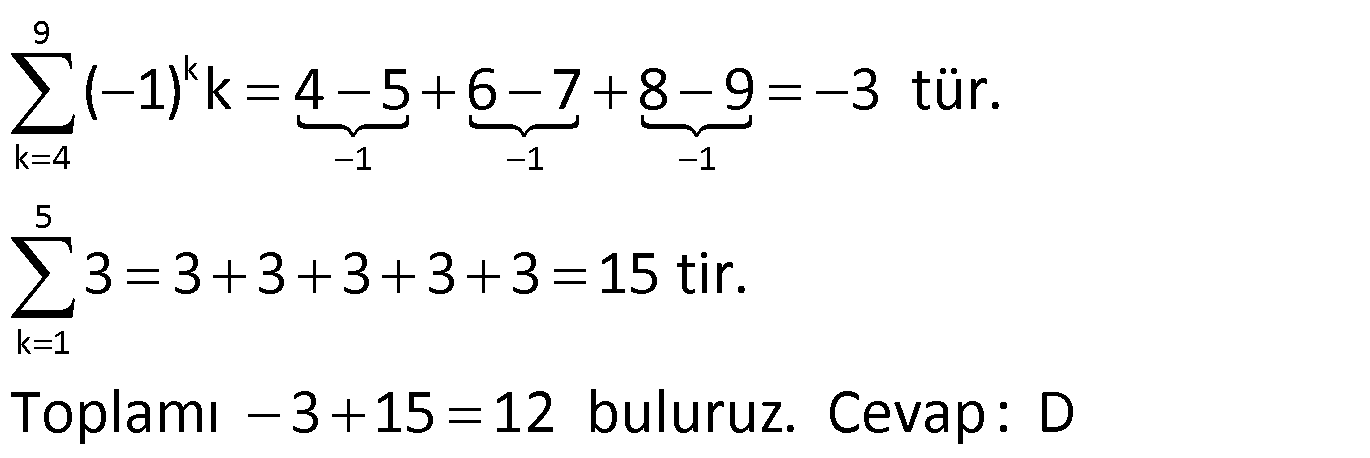
5.SORU
| | | | | |
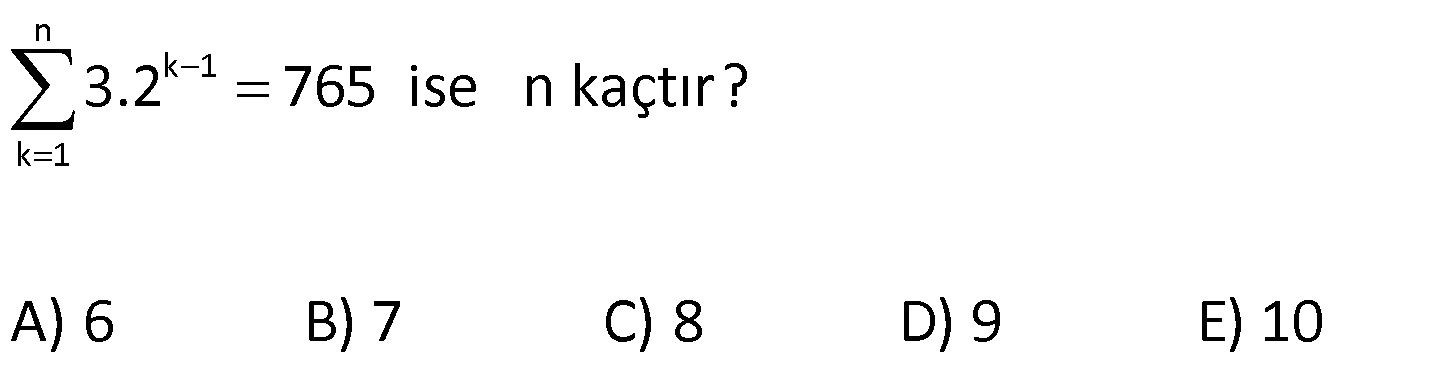
Çözüm için Tıklayınız.
6.SORU
| | | | | |
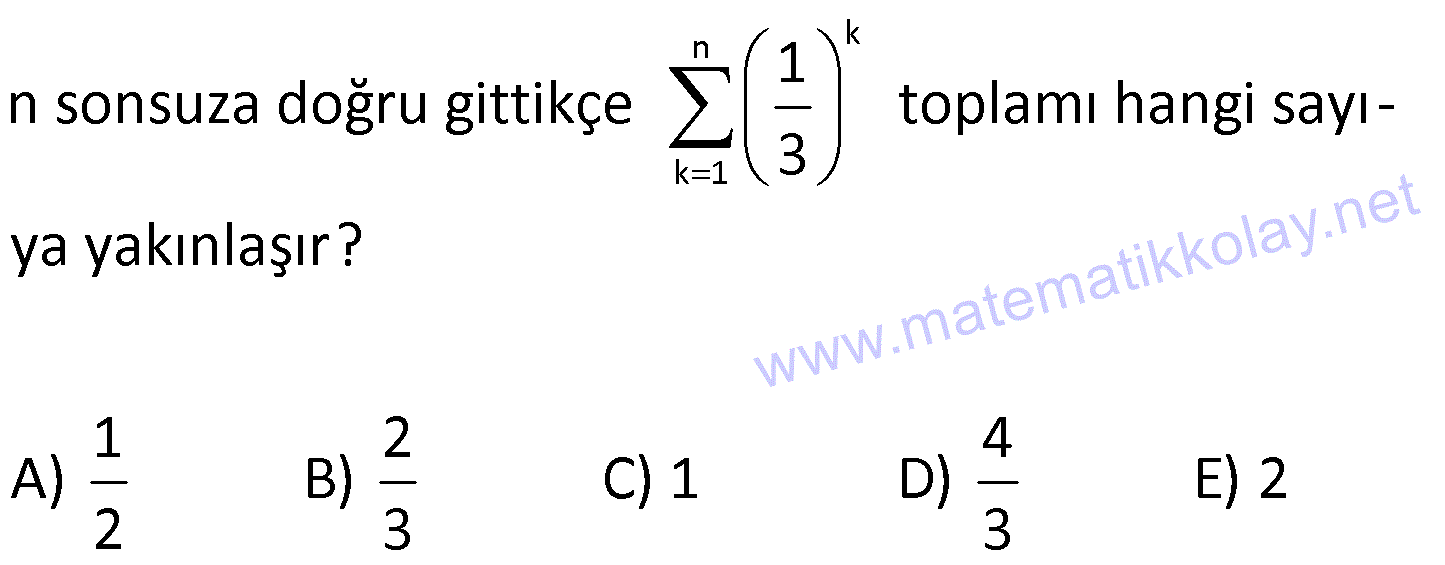
Çözüm için Tıklayınız.
7.SORU
| | | | | |
Çözüm için Tıklayınız.
8.SORU
| | | | | |
Çözüm için Tıklayınız.
Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
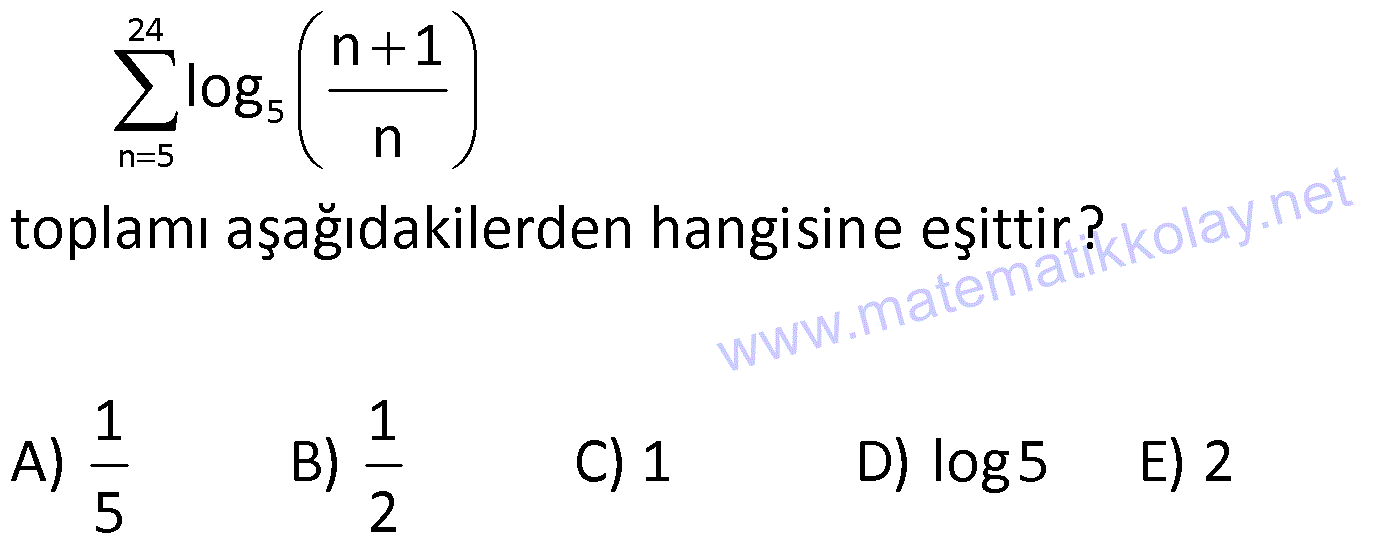
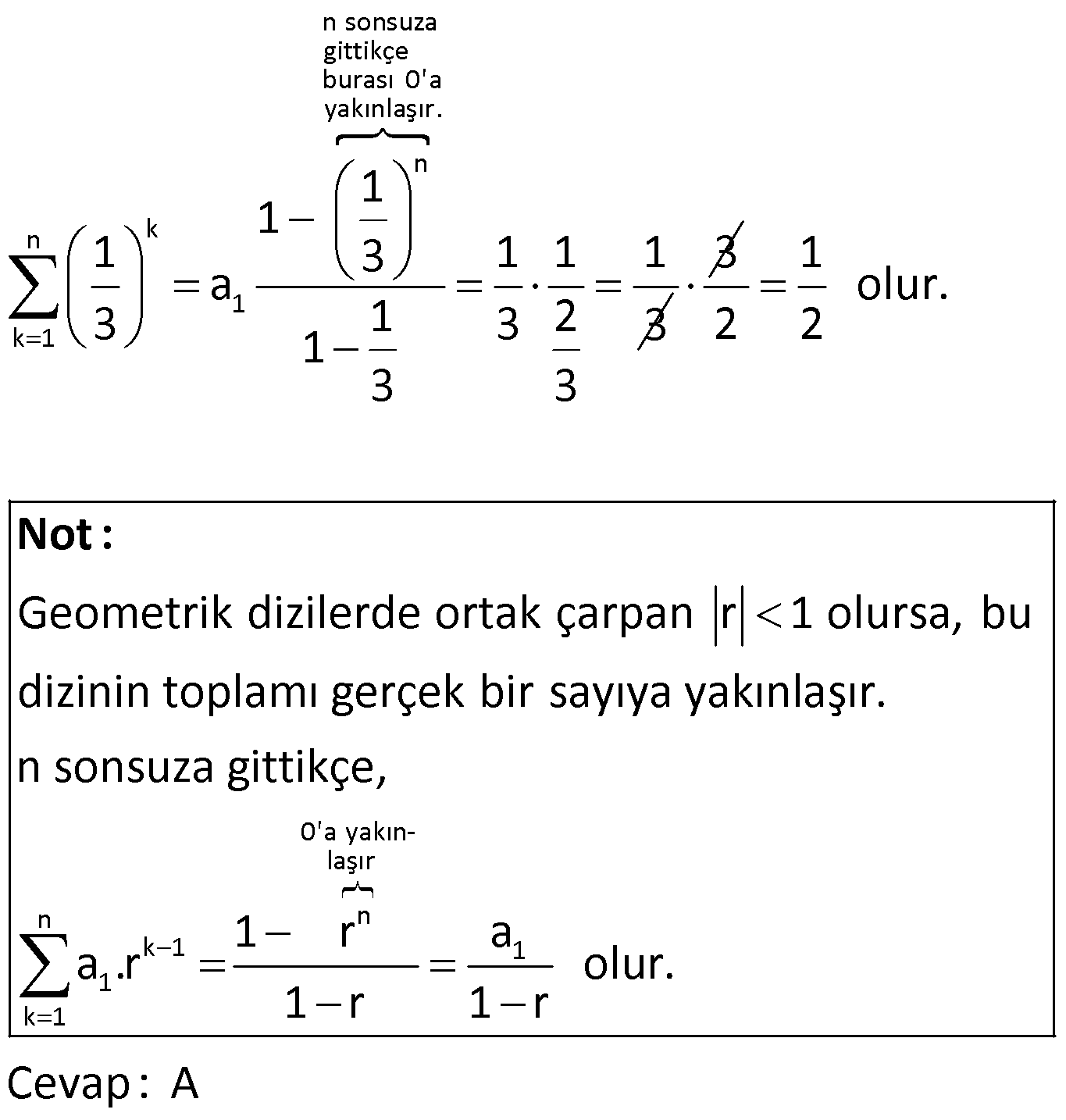
TOPLAM SEMBOLÜ VE FIBONACCI www.matematikkolay.net 1) 25 50 100 n 1 n 2 n 4 10 10 2 2 n 1 n 1 4 8 12 16 100 … 7 15 23 31 199 toplamı aşağıdakilerden hangisine eşittir? 4n 2n n A) B) C) 8n 1 5n 3 n 3 n 2n D) E) 6n 1 4n 3 ÇÖZÜM: Üst Sınır indis Alt sınır n 1 2 3 n k k 1 Dizinin kuralı n k k k 1 5 k 1 a a a … a toplamını a olarak ifade edebiliriz. Alt k 1 den n’e kadar a terimlerinin a toplamıdır. Mesela 2k 2 4 6 8 10 dur. Sorudaki kesirlerin pay kısmı 4, 8, 12, 16 şeklinde ilerliyor. Yani hep 4’ün katı şeklinde ilerliyor. 4n Payda ise 7, 15, 23, 31, … şeklinde ilerliyor. 8’in katlarından 1 eksik şeklinde O halde bu rayı da 8n 1 olarak ifade edebiliriz. n 1 den başlarsak, son terim 4n 100 n 25 olur. 4n n 1 den 25’e kadar terimlerinin toplamı 8n 1 olarak ifade ede 25 n 1 biliriz. Yani 4n dir. Cevap : A 8n 1 2) 24 5 n 5 n 1 log n toplamı aşağıdakilerden hangisine eşittir ? 1 1 A) B) C) 1 D) log 5 E) 2 5 2 ÇÖZÜM: 24 5 n 5 5 5 5 5 5 n 1 log n 6 7 8 25 log log log … log 5 6 7 24 6 log 7 5 6 8 7 25 24 5 log 5 1 dir. Cevap : C 3) 10 n 1 1 (n 1)! n! toplamı aşağıdakilerden hangisine eşittir ? 11! A) 2.5! B) C) 11! 2 D) 10! E) 11! 2 ÇÖZÜM: 10 n 1 1 (n 1)! n! 1 2! 1! 3! 2! 4! 3! … 11! 10! 1 11! 1! 11! olur. Cevap: E 4) 9 5 k k 4 k 1 ( 1) k 3 toplamı kaçtır? A) 10 B) 2 C) 8 D) 12 E) 18 ÇÖZÜM: 9 k k 4 1 1 1 5 k 1 ( 1) k 4 5 6 7 8 9 3 tür. 3 3 3 3 3 3 15 tir. Toplamı 3 15 12 buluruz. Cevap: D www.matematikkolay.net 5) n k 1 k 1 3.2 765 ise n kaçtır? A) 6 B) 7 C) 8 D) 9 E) 10 ÇÖZÜM: k 1 n 1 3.2 dizisi bir geometrik dizidir. İlk terimi 3 tür. (k 1 için) Ortak çarpanı 2 dir. 1’den n’e kadar n terim vardır. Buna göre, 1 r a formülü ile toplamlarını hesaplayabiliriz. 1 r 3 n 1 2 765 1 2 255 n n 1 2 255 256 2 n 8 dir. Cevap : C 6) k n k 1 1 n sonsuza doğru gittikçe toplamı hangi sayı – 3 ya yakınlaşır? 1 2 4 A) B) C) 1 D) E) 2 2 3 3 ÇÖZÜM: n sonsuza gittikçe burası 0’a yakınlaşır. n k n 1 k 1 1 1 1 1 1 1 3 a 3 3 1 2 3 1 3 3 3 0’a yakın- laşır n n k 1 1 1 k 1 1 olur. 2 2 Geometrik dizilerde ortak çarpan r 1 olursa, bu dizinin toplamı gerçek bir sayıya yakınlaşır. n sonsuza gittikçe, 1 r a a .r olur. 1 r 1 r Cevap : A Not : 7) Fibonacci dizisindeki en küçük 5.asal sayı kaçtır? A) 5 B) 13 C) 37 D) 89 E) 119 ÇÖZÜM: n n İlk iki terimi 1 olup; daha sonraki her terimin, kendinden önceki iki terimin toplamı şeklinde olan diziye Fibonacci dizisi denir. F 1,1,2,3,5,8,… şeklindedir. Parçalı fonksiyon olarak yazarsak, F n 1 n 2 1.asal 2.asal 3.asal 4.asal 5.asal 1 n 1,n 2 F F n 2 Buna göre, Fibonacci dizisini açarak yazalım. 1,1, 2 , 3 , 5 ,8, 13 ,21,34,55, 89 5.asal sayısı 89 dur. Cevap : D 8) x, y, z, t sayıları sırasıyla Fibonacci dizisinin ardışık terimleridir. x y z t 521 x t 288 olduğuna göre, x kaçtır? A) 55 B) 89 C) 144 D) 283 E) 377 ÇÖZÜM: a x a 2x a x 2a 3x a 2x 2a 3x a x x’den önceki terim a olsun. y a x tir. z x y a 2x tir. t y z 2a 3x tir. x t 288 2a 4x 288 tir. x y z t 521 4a 7x 521 dir. 4a 7x 521 2 / 2a 4x 288 4a 7x 521 4a 8x 576 x 55 x 55 tir. Cevap: A
