11.SORU

| | | | | |
Çözüm için Tıklayınız.

12.SORU

 | | | | |
Çözüm için Tıklayınız.
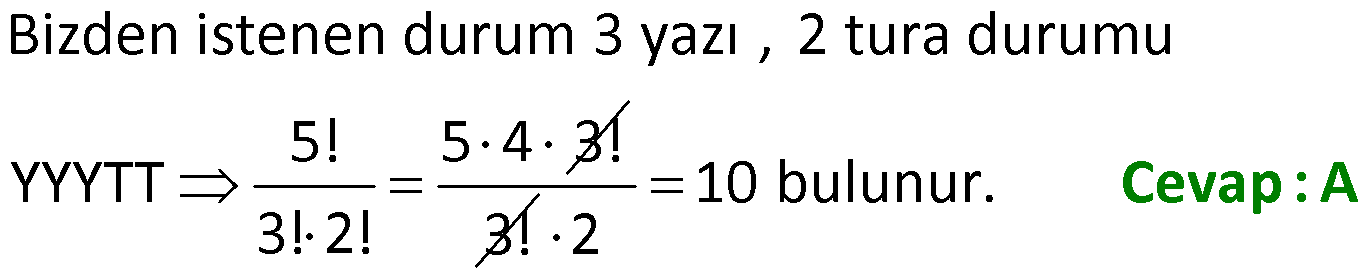
13.SORU

| | | | | |
Çözüm için Tıklayınız.

14.SORU

| | | | | |
Çözüm için Tıklayınız.

15.SORU

| | | | | |
Çözüm için Tıklayınız.

16.SORU

| | | | | |
Çözüm için Tıklayınız.

17.SORU

 | | | | |
Çözüm için Tıklayınız.

18.SORU
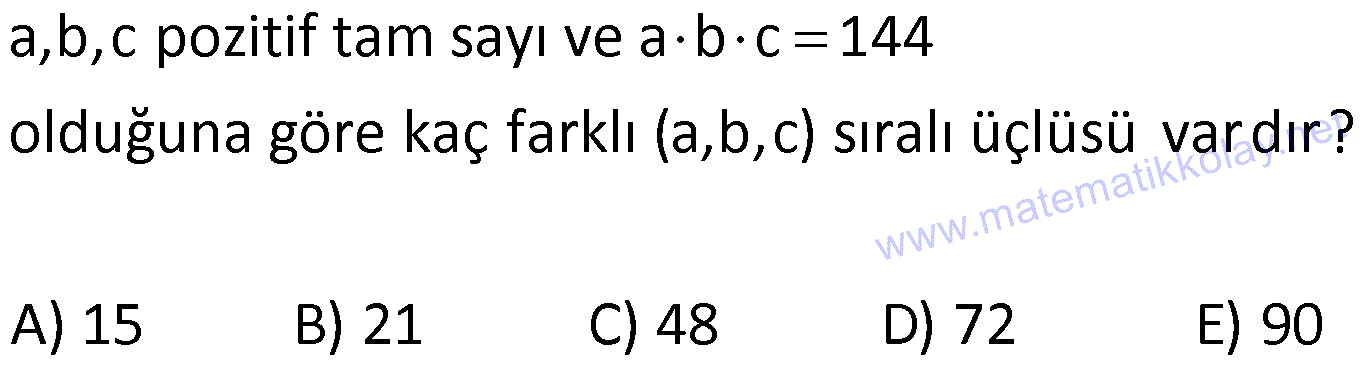
| | | | | |
Çözüm için Tıklayınız.

Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
11) Bir otobüs terminalinde bulunun yiyecek ve içecek otomatında 4 tane gofret, 3 tane su, 2 tane kraker kalmıştır. Her ürün çeşidi bulunduğu bantta tek sıra halinde durmaktadır ve öndeki ürün düşmeden arkadaki ürün düşmemektedir.Bu 9 ürün bittiğinde kaç farklı sıralamada alınmış olur? A) 1400 B) 1260 C) 960 D) 630 E) 288 ÇÖZÜM: Burda dikkat edeceğimiz şey aynı ürünler kendi aralarında yer değiştiremeyecek. 9! 9 8 GGGGSSSKK 4! 3! 2! 4 7 6 5 4! 4! 6 2 1260 bulunur. Cevap : B 12) 5 madeni para rastgele atılıyor. 3’ünün yazı, 2’sinin tura geldiği kaç durum vardır? A) 10 B) 20 C) 24 D) 30 E) 60 ÇÖZÜM: Bizden istenen durum 3 yazı , 2 tura durumu 5! 5 4 3! YYYTT 3! 2! 3! 10 bulunur. 2 Cevap : A 13) 5 madeni para rastgele atılıyor. Kaç durumda yazı sayısı tura sayısından daha azdır? A) 8 B) 12 C) 16 D) 20 E) 24 ÇÖZÜM: 5 parada yazı sayısı turadan az olsun isteniyor. 3 durum vardır. 5! YYTTT 10 dur. 2! 3! 5! YTTTT 5 tir. 4! 5! TTTTT 1 dir. 5! Toplam 10 5 1 16 bulunur. 5 para için 2 2 2 I .Durum: II.Durum: III.Durum: II.Yol: 5 2 2 2 32 durum vardır. Bunların yarısında tura sayısı yazı sayısından fazladır, yarısında yazı sayısı tura sayısından fazladır. 32 16 bulunur. 2 Cevap : C 14) Bir lunaparkta her oyuncakta kullanılabilecek özdeş 5 jeton 5 çocuğa kaç farklı şekilde dağıtılabilir? A) 60 B) 63 C) 120 D) 126 E) 140 ÇÖZÜM: TEKRARLI PERMÜTASYON Özdeş nesnelerin dağıtımında ayraç yöntemi kullanı lır. Jetonları O harfiyle gösterelim.Yöntemi kavramak için şöyle bir mantık kullanabiliriz.Biz bu jetonları 5 çocuğa pay edeceğiz.Bir bütünü 5 parçaya ayırmak için 4 kesim yapılır. Bu yüzden 4 tane ayraç (ayırıcı) kullanıcağız. Mesela her çocuğa 1 er jeton verilme durumunun gösterimi O / O / O / O / O şeklindedir. Buna göre 5 jeton ve 4 a yracı sıralayalım. 9! 9 8 5! 4! 7 6 2 5! 5! 24 3 126 bulunur. Cevap : D 15) Bir ekmek fırınında her müşteri en az 2 ekmek almaktadır. 15 tane ekmek 4 müşteriye kaç farklı şekilde satılmış olabilir? A) 70 B) 105 C) 120 D) 180 E) 210 ÇÖZÜM: Her müşteri en az iki ekmek alacağı için önce 2 şer ekmek dağıtalım. 15 4 2 7 ekmek kalır. Şimdi 7 ekmeği 4 müşteriye dağıtalım. Ekmekler özdeş kabul edilir. Ayraç yöntemi kullanıcağız. 4 kişi için 4 1 3 ayraç kullanırız. O O O O O O O / / / 10! 10 9 8 7! 7! 3! 7! 10 72 6 12 6 120 bulunur. Cevap : C 16) Rakamları toplamı 6 olan en çok 4 basamaklı kaç farklı sayı yazılabilir? A) 56 B) 84 C) 140 D) 168 E) 210 En çok dört basamaklı dediği için biz a,b,c,d şeklinde 4 rakam düşünelim. Oluşturacağımız abcd sayılarında a 0 olursa sayı 3 basamaklı, a b 0 olursa sayı 2 basamaklı ve son olarak a b c 0 olursa sayı 1 basamaklı olur. 6 tane 1 i ayraç yöntemiyle a,b,c ve d rakamlarına dağıtalım. 4 değişken için 4 1 3 ayraç kullanılır. 111111 / / / 9! 9 8 7 6! 6! 3! 6! 72 6 12 7 6 84 bulunur. Cevap : B 17) Rakamları toplamı 6 olan 4 basamaklı kaç farklı sayı yazılabilir? A) 56 B) 84 C) 140 D) 168 E) 210 ÇÖZÜM: abcd şeklinde 4 basamaklı sayılar oluşturacağız. a b c d 6 olduğu için 6 tane 1 i ayraç yöntemi ile a,b,c ve d ye dağıtacağız. Sayının 4 basamaklı olduğunu garanti etmek için a ya başta bir tane 1 i vere lim.5 tane 1 kaldı. 5 tane 1 i 4 harfe 3 ayraç ile dağıtırız. 8! 8 7 6 11111 / / / 5! 3! 5! 5! 6 56 bulunur. Cevap : A 18) a,b,c pozitif tam sayı ve a b c 144 olduğuna göre kaç farklı (a,b,c) sıralı üçlüsü vardır? A) 15 B) 21 C) 48 D) 72 E) 90 ÇÖZÜM: TEKRARLI PERMÜTASYON 2 4 2 a b c 144 a b c (12) 2 3 Şimdi a,b ve c ye bu sayıları dağıtalım. 4 tane 2 yi a,b ve c ye 2 ayraç ile dağıtırız. 6! 6 5 4! 2222 / / 4! 2! 4! 15 tir. 2 2 tane 3 ü a,b ve c ye 2 ayraç ile dağıtırız. 4! 24 33 / / 6 dır. 2! 2! 4 (a, b, c) lerin sayısı 15 6 90 bulunur. Cevap : E



Merhaba, 4. soruda sadece ortada sıralanan kalemleri tekrarlı permütasyon olarak değerlendirdiniz ve başa ve sona konulan kalemlerin 4 – 2 kalemden biri olma ihtimalini göz önüne almadınız. Böyle yapsaydınız sonuç nasıl olurdu?
Özdeş oldukları için bunu diyemeyiz. Başa konulacak mavi kalem için, hangi maviyi seçtiğimizin bir önemi yok. Sadece ortada sıralanacak mavi kalemlerden birisinin eksilmesini sağlar. Aynı şey sona konulan kırmızı kalem için de geçerli.
2. soruda sadece 1 tı yeterli değil mi? ıtrtıl sayılmaz mı mesela
Olmaz. Her t den sonra ı gelmesi isteniyor.