Sayma

1.Sayfa için Tıklayınız.

11.SORU

Çözüm için Tıklayınız.

12.SORU


Çözüm için Tıklayınız.

13.SORU

Çözüm için Tıklayınız.

14.SORU

Çözüm için Tıklayınız.

15.SORU

Çözüm için Tıklayınız.

16.SORU

Çözüm için Tıklayınız.

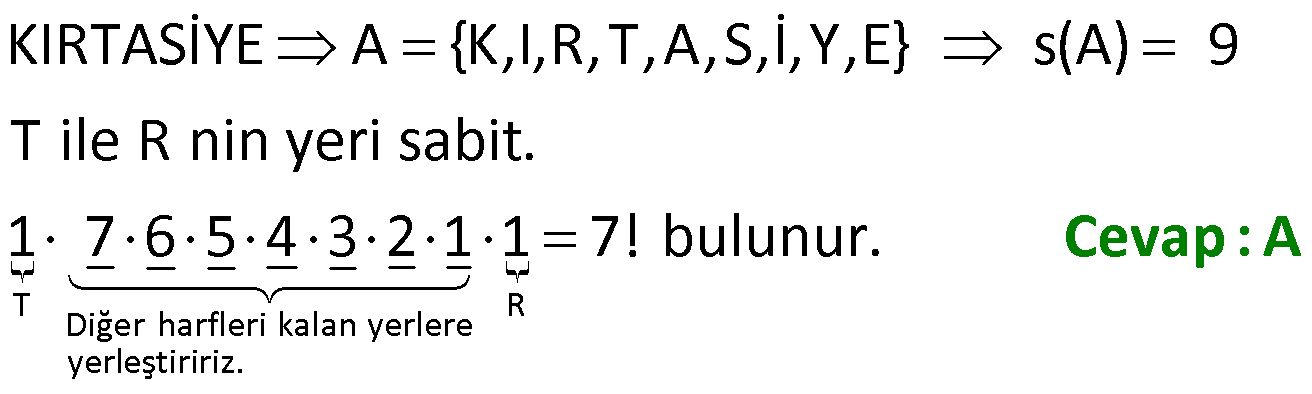
17.SORU

Çözüm için Tıklayınız.

18.SORU

Çözüm için Tıklayınız.

19.SORU

Çözüm için Tıklayınız.

20.SORU

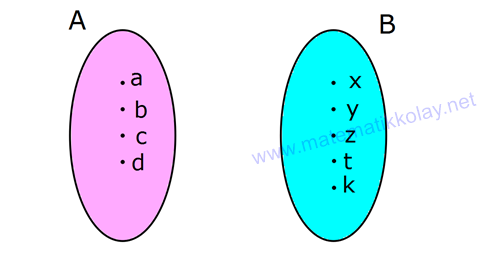
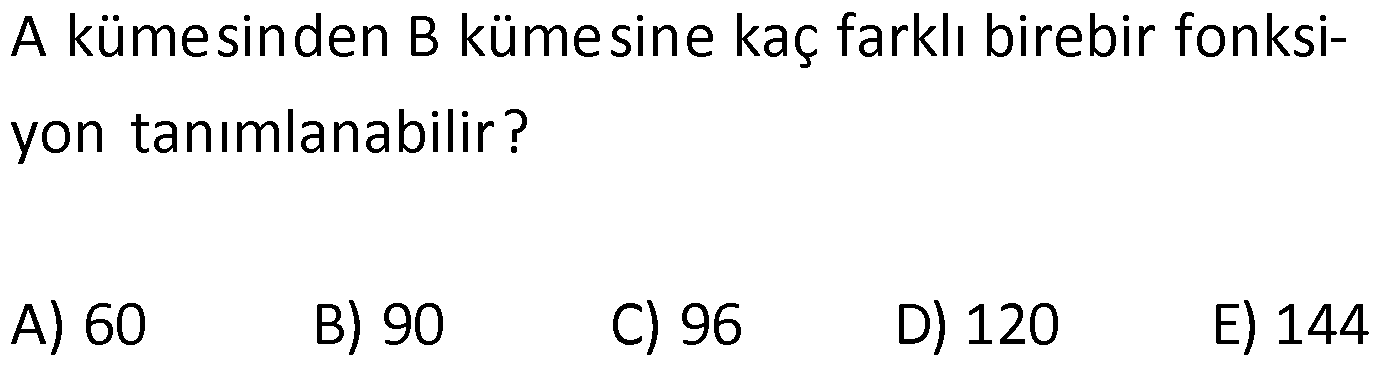
Çözüm için Tıklayınız.

21.SORU

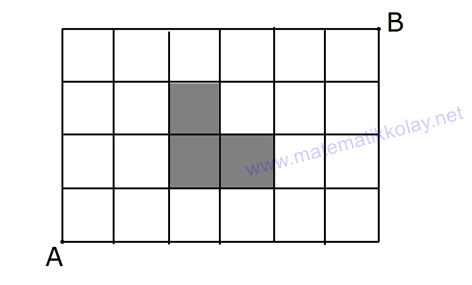
Çözüm için Tıklayınız.

Bu Test Bitti. Diğer Çözümlü Testler için Tıklayabilirsiniz.
Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.) 11) A {0,1,2,3,4,5,6} kümesinin elemanları ile rakamları farklı 300 ile 600 arasında 5 ile bölünebilen kaç farklı sayı yazılabilir? A) 25 B) 30 C) 32 D) 40 E) 42 ÇÖZÜM: 5 olsun Yalnızca Geriye 0 gele kalan 5 rakamdan biri gelebilir. Bir sayının 5 ile bölünmesi için birler basamağı ya 0 ya da 5 olmalı. Bu soruda yüzler basamağına 5 gelme durumunu ayrı incelemeliyiz. 1 5 1 0 ve 5 3 veya 4 ten biri bir. gelebiir. gelebilir. Geriye kalan 5 rakamdan biri gelebilir. 2 5 2 5 20 25 bulunur. Cevap : A 12) Sayma www.matematikkolay.net A {1,2,3,4,5} kümesinin elemanları ile yazılabilecek rakamları farklı 3 basamaklı sayılar küçükten büyüğe sıralanırsa 421 sayısı kaçıncı sayı olur? A) 39 B) 40 C) 41 D) 42 E) 43 ÇÖZÜM: 1,2,3 ten biri Geriye gelebilir. Geriye kalan kalan 4 rakamdan 3 rakamdan biri gelebilir. biri gelebilir. Önce 400 den küçük kaç sayı yazabiliriz, onu bulalım. 3 4 3 36 sayı Şimdi 41 le başlayanlara bakalı 4 1 geriye kalan 3 rakamdan biri gelebilir. m. 1 1 3 3 sayı yazılabilir. 39 sayıyı geride bıraktık. 421 sayısı onlar basamağı 2 olan en küçük sayıdır. Dolayısıyla bir sonraki sayı 421 dir. 39 1 40. sayı olur. Cevap : B 13) A {1,2,3,4,5} kümesinin elemanları ile yazılabilecek 3 basamaklı çift sayıların toplamı kaçtır? A) 15000 B) 15500 C) 16500 D) 16650 E) 17500 ÇÖZÜM: tüm tüm 2 veya rakamlar rakamlar 4 ten biri gelebilir. gelebilir. gelebilir.. Önce tüm sayıların kaç tane olduğunu bulalım. 5 5 2 50 sayı yazılır. 50 sayının yarısının 1 ler basamağı 2 yarısının da 4 tür 10’ar Yüzler Onlar 5 farklı rakamın toplamı kez . Diğer basamaklara ise her rakam 10’ar defa gelir. Yüzler ve onlar basamağına eş sayıda gelirler.İkisinin basamak değeri toplamı 110 dur. 10 110 (1 2 3 4 5) 25’er Birler kez 25 . 1 .(2 4) 1100 15 25 6 16500 150 16650 bulunur. Cevap : D 14) 4 farklı oyuncak 5 çocuğa her çocuğa en çok bir oyuncak verilmek üzere kaç farklı şekilde dağıtılabilir? A) 720 B) 625 C) 360 D) 125 E) 120 ÇÖZÜM: I. oyuncak III. oyuncak II. oyuncak IV. oyunc için 5 seçenek için 3 seçenek için 4 seçenek var var var Her oyuncağı sırayla dağıtalım.Bir çocuğa birden fazla oyuncak veremeyeceğimize dikkat edelim. 5 4 3 2 ak için 2 seçenek var 120 bulunur. Cevap : E 15) 20 19 18 17 20 soruluk bir testte her sorunun 5 seçeneği vardır. Ard arda gelen herhangi 3 sorunun cevabı aynı olma￾mak şartıyla kaç değişik cevap anahtarı hazırlanabilir? A) 3 B) 5 3 C) 20 3 D) 60 2 E) 120 17 2 ÇÖZÜM: 18 tane 3 ilk soru 3 soru için 2. soru için Bundan sonra için 5 de 3 seçenek var 4 seçenek var her soru için seçenek var 3 seçenek var Her soru için seçeneklerimizi sıralayalım. 5 4 3 3 3 … 3 2 18 0 3 bulunur. Cevap : C 16) KIRTASİYE kelimesinin harfleriyle yazılabilecek anlamlı ya da anlamsız kelimelerin kaç tanesi T ile başlayıp R ile biter? A) 7! B) 7!.2 C) 8! D) 8!.2 E) 9! ÇÖZÜM: T R Diğer harfleri kalan yerlere yerleştiririz. KIRTASİYE A {K,I,R,T,A,S,İ,Y,E} s(A) 9 T ile R nin yeri sabit. 1 7 6 5 4 3 2 1 1 7! bulunur. Cevap : A Sayma www.matematikkolay.net 17) KASİYER kelimesinin harfleriyle yazılabilecek anlamlı ya da anlamsız kelimelerdan kaç tanesinde herhangi iki sesli harf yan yana gelmez? A) 7! B) 4! 3! C) 20 5! D) 2 6! E) 6! ÇÖZÜM: 4 farklı yere 4! şekilde yerleşirler. KASİYER A {K,S,Y,R,A,E,İ} İlk olarak sessiz harfleri yerleştirelim. 4 3 2 1 4! Şimdi 3 sesli harfi yerleştirebileceğimiz kaç yer var ona bakalım. Sessiz sesli harflerin sessizlerin 6 sıralaması sıralaması Sessiz Sessiz Sessiz Sesli harfleri yerleştirebileceğimiz 5 yer var.Sırayla her sesli harfi yerleştirirsek 5 4 3 4! 2 2 3 5 4! 2 6! bulunur. Cevap : D 18) KALEM kelimesinin harfleriyle yazılabilecek anlamlı ya da anlamsız kelimeler soldan sağa alfabetik olarak sıralandığında sondan 74. kelime aşağıdakilerden hangisidir? A) LMKEA B) LKMEA C) EMLAK D) EMLKA E) ELMKA ÇÖZÜM: KALEM kelimesinin harflerini alfabetik sıralarsak; A, E, K, L, M olur. Kelimede 5 harf olduğundan 5! 120 kelime yazılır. 120 24 Her harfle başlayan 24 kelime yazılır. 5 Sondan 74.kelimeyi bulmaya çalışa lım. 24 3 72 olur. M, L, K ile yazılan kelimeler biter. 74. kelime E ile başlayan sondan 2. kelime olur. 73 kelime EMLKA 74.kelime EMLAK olur. Cevap : C 19) 4 farklı boya ile şekildeki gibi 9 birim kare boyana￾caktır. Aynı renk boyalar kenarları ya da köşeleri ortak olan karelere gelmeyecek şekilde kaç türlü boyama yapılır? A) 72 B) 144 C) 288 D) 360 E) 480 ÇÖZÜM: 1 satır 1.satır 1. satır 1. sütun 2. sütun 3. sütun 2 sat İlk satırı yerleştirerek başlayalım. 4 3 3 36 İkinci satıra direk 2 renk ihtimaliyle başlarız. Üstündeki ve çaprazındaki kareden farklı renk olmalı. 2 ır 2 satır 2. satır 1. sütun 2. sütun 3. sütun 1 1 2 Üçüncü satır 2. satır gibi olur. 2 Hepsini çarpalım. 36 2 2 144 bulunur. Cevap : B 20) Sayma www.matematikkolay.net A kümesinden B kümesine kaç farklı birebir fonksi￾yon tanımlanabilir? A) 60 B) 90 C) 96 D) 120 E) 144 ÇÖZÜM: Fonksiyonun temel kuralı gereği tanım kümesinde boşta eleman kalmamalı, her birinin tek bir karşılığı olmalı. Birebir olması için ise farklı elemanların görün￾tüleri farklı olmalı. a yı eşleyerek başlay a için c için b için d için alım ve azaltarak ilerleyelim. 5 4 3 2 120 bulunur. Cevap : D 21) Şekildeki A noktasında bulunan bir karınca sadece çizgiler üzerinden ilerleyecek ve ortadaki engelin çizgilerinden kesinlikle geçmeyecektir.Buna göre A da B ye en kısa yoldan kaç farklı şekilde gidebilir? A) 10 B) 15 C) 20 D) 24 E) 32 ÇÖZÜM: A noktasından harekete başlayacak. Buraya 1 yaza￾lım. Bundan sonra gideceği her köşeye, o köşenin ya solundan gelebilir ya da altından gelebilir. Bu kurala göre şekildeki gibi toplayarak ilerlersek 10 farklı şekilde B noktasına gidebileceğini buluruz. Cevap : A  
Sayfalar: 1 2

“Sayma” üzerine 23 yorum

    • Hayır. Ard arda gelen herhangi üç sorunun cevabı aynı olmayacak denmiş. Yani bir sorunun cevabı önceki 2 soruyla aynı olamaz. Bu sebeple 3 seçenek kalır.

      • 1’i başa yazdıktan sonra, birler basamağına rakam yazıyoruz. En son, onlar basamağına rakam koyuyoruz. O yüzden 5 seçenek kalıyor.

  6. 10. soruda sanırım bir hata var nedeni şu:
    3 basmaklı ve 1 basmaklı sayıları doğru hesaplamışsınız tmmda ama 2 basamaklılarda yanlış hesaplama var soru rakamları farklı demiş siz son basamağa 1,3,5 yazmışsınız 2. basamağada sıfır hariç ve bir tane sayı 1ler basamğında kullandığı için onlar basamğına 5 yazmışsınız bu yanlış habuki bu yanlış gerçek cevap bence böyle olmalıydı;rakamları farklı dediği için 1ler basmağını ayrı incelememiz lazm yani 3 adet 2 bas. sonra bunları toplayacaktık

    • Çözümü tekrar inceledik ama hata göremedik.
      İki basamaklı, rakamları farklı tek sayılar yine 15 tane çıkıyor. İstersen tek tek yazalım.
      13, 15, 21, 23, 25, 31, 35, 41, 43, 45, 51, 53, 61, 63, 65

  9. Abi karantinadayim k3ndim çalışmaya çalışıyorum hoca falan yok hiç birsey anlamadım bir 5ane böle soru doğru yapamadım. ağlamak :(😱

Yorum yapın