Bu bölümde Tek Çift Sayılar ile ilgili 5 adet soru bulunmaktadır. Sorularınızı çözdükten sonra “Doğru Cevap” seçeneğine tıklayarak doğru şıkkı görebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
1.SORU

| | | | | |
Çözüm için Tıklayınız.
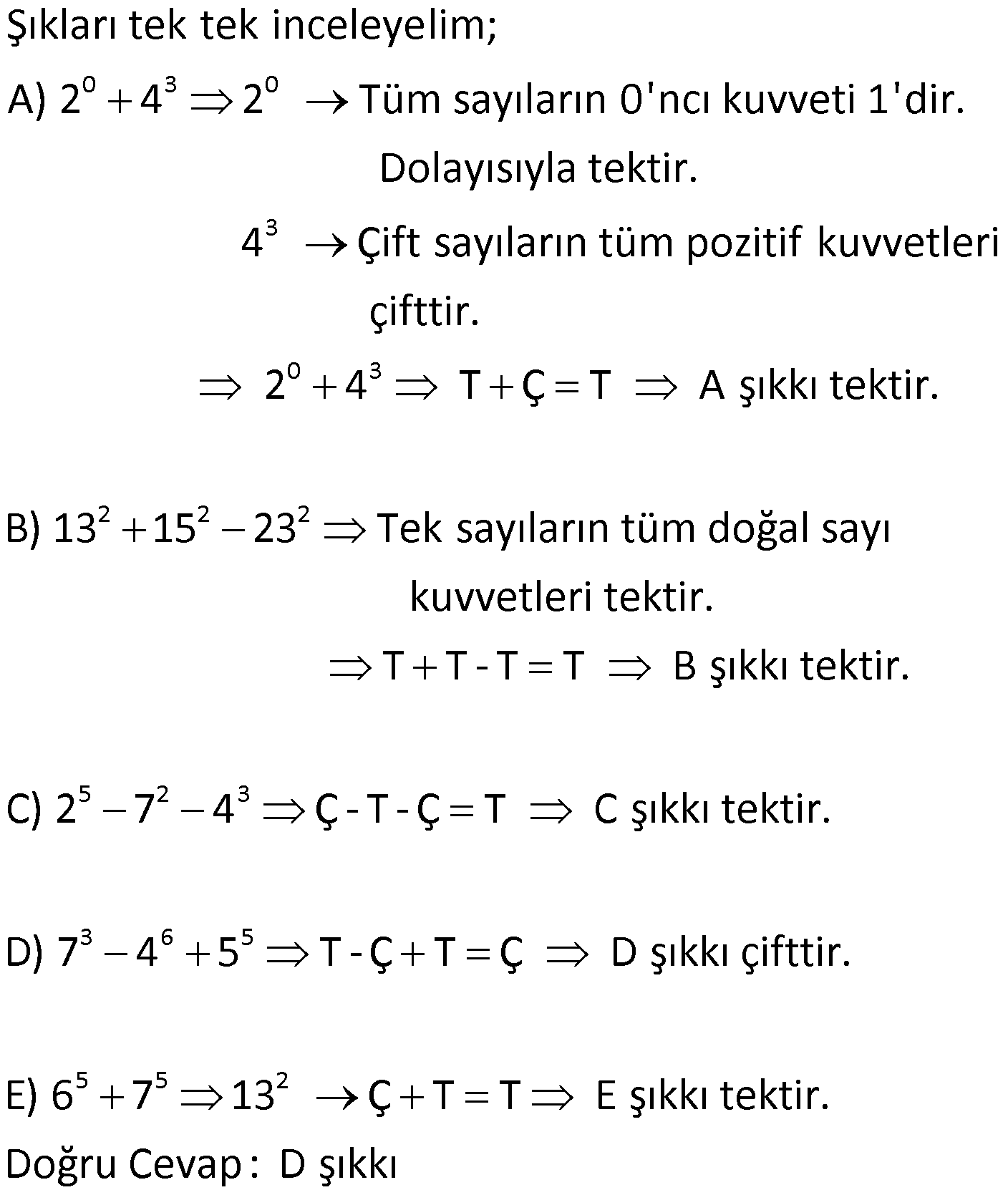
2.SORU

| | | | | |
Çözüm için Tıklayınız.

3.SORU

 | | | | |
Çözüm için Tıklayınız.

4.SORU

| | | | | |
Çözüm için Tıklayınız.

5.SORU
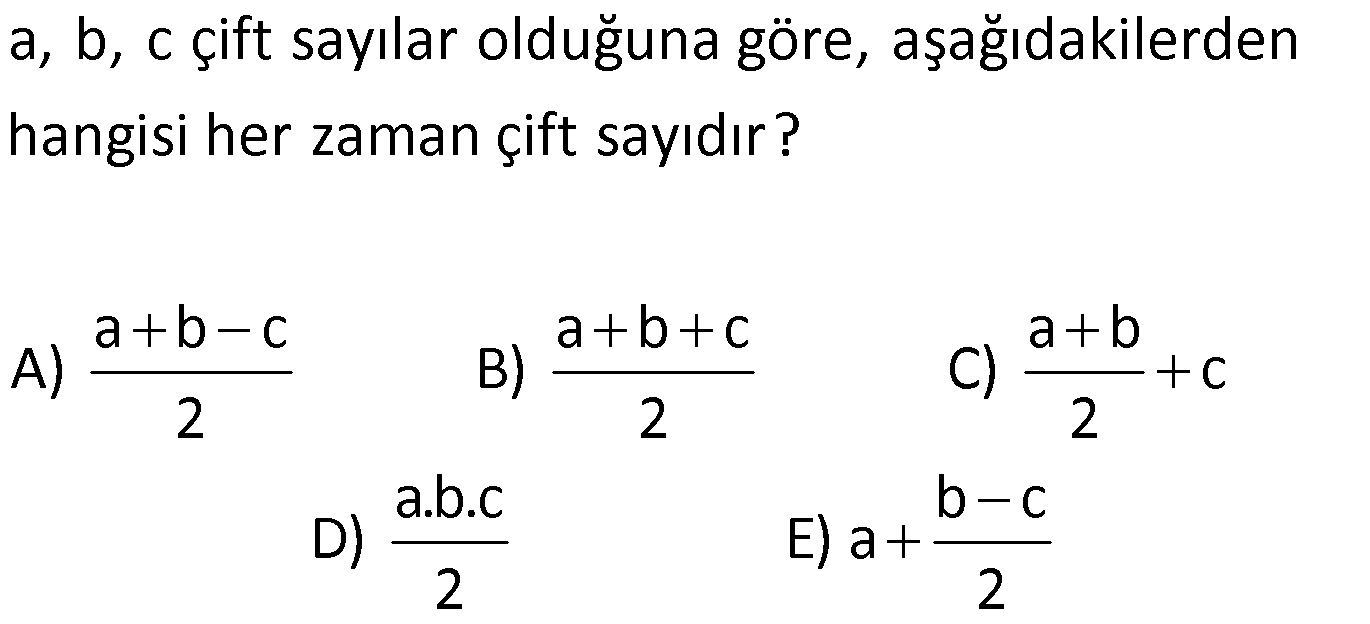
| | | | | |
Çözüm için Tıklayınız.

Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)



2. soruda a=0 olursa C seçeneği tek olur.
a=0 olursa a^2+a=0+0=0 olur. Bu da bir çift sayıdır.
Aslında rakam koymaya bile gerek yok 7a+4 çift ise toplamada çift + çift sadece çift sayı verebilir. yani
7a+4[çift] olduğu gibi 7a da çift olması gerektiği için 7[tek sayı ile hangi sayıları çarparsan çift sayı çıakr ortaya çift sayıları çarparsan yani a da o yüzden kesinlikle çift olmak zorunda.
hocalarım Selamun Aleyküm. Tek ve çift sayılarda bölünme olmuyor diye biliyorum ama 5 inci soruda yapılmış.
Aleyküm selam. O şekilde bir genelleme yapamayız. Sorunun çözümünde de bir hata gözükmüyor.
tek-çift sayıların rasyonel sayıları olmaz işlem bütünlerinin değil, yani işlemde diyor ki a,b,c çift sayı oldukları için hepsi bu sayıları toplasan da çıakrtsan da çarpsan sonuçları hep çift sayı çıkacağı için, tüm çift sayılar 2 ile tam bölünebilir.
Bölme olmuyor zatn onun çözümü a b C yerine bölmeli sorularda 2a 2b 2c koymak lazım yoksa değer verirsen çift de tek de çıkıyor şaşırtıyor.
5.soruda ABC çift sayılardır demiş tam sayılardır demesi gerekmiyormu
Teklik çiftlik kavramı tam sayılar için geçerli olduğu için ekstra belirtmesine gerek yok.
Aynen oyle olmaliydi
5. soruda a,b,c çift sayılar deniliyuor. İşlem çözümünde 0 da ele alailirsiniz. Neden a ya 2x ye 2y, c ye de 2z denilerek ilerlendi. Değer verilerek yapılama mı . Mesela a ya 0, B ye 2, C ye de 4 deriz. Soruda Pozitif tam sayı vb. bir ayrımın yapılması gerek miyor mu. Yardım 😉
2x, 2y ve 2z denilerek, olabilecek tüm durumlar ele alınmış oluyor. a, b, c sayıları 0 da olabilir, negatif çift sayılar da olabilir. Pozitif olacak diye bir şarta gerek yok. Bu sayıların çift olduğunu bildiğimiz için, herhangi bir tam sayının 2 katıdır, diye ifade edebiliriz. Buna 0 da dahil. (x=0 olursa, a=2x=2.0=0 olur.) Yani hiç bir durumu atlamamış oluyoruz.
bu sorular tyt seviyesinde mi acaba
Evet.
5.Soruda a,b,c lere 0 verince 2 ile böldüğümüzde rayonel bir sayı çıkıyor anlamadım burayı kısaca anlatır mısınız?
0/2 kesri 0 a esittir. Yani ayni zamanda bir tamsayidir. Bu yuzden cift sayi olma özelliği hala sağlanır.
5 soruda cevap (D) demişsiniz a,b,c /2 de abc üçünede 0 verirseniz cevap 0/2 diye cıkar soruda farklı sayılar dememiş yani soru hatalı
0/2 de 0’a eşittir. Dolayısıyla yine çift bir tamsayıdır.
* 0 sayısı ne negatif ne de pozitif bir sayıdır .
Orta da ‘dır.
Soru hatalı değil
5. soruda 2x 2y diye değer vermişiz de sonra da d şıkkı hariç diğerlerinde kesinlik yok demişsiniz zaten hepsini çift düşünürsek a şıkkından örnek verecek olursam x+y-z hepsini çift düşünürsek sonuç çift çıkar
x, y ve z nin çift olduğu garanti değil, A şıkkı kesinlikle çift diyemeyiz.
Son sorud hepsine 2 değer verirsek,2.2.2=6/2=3 çıkabilir. Yardımci olur musunuz?
2.2.2=8 yapar. 8/2=4 olur.