11.SORU
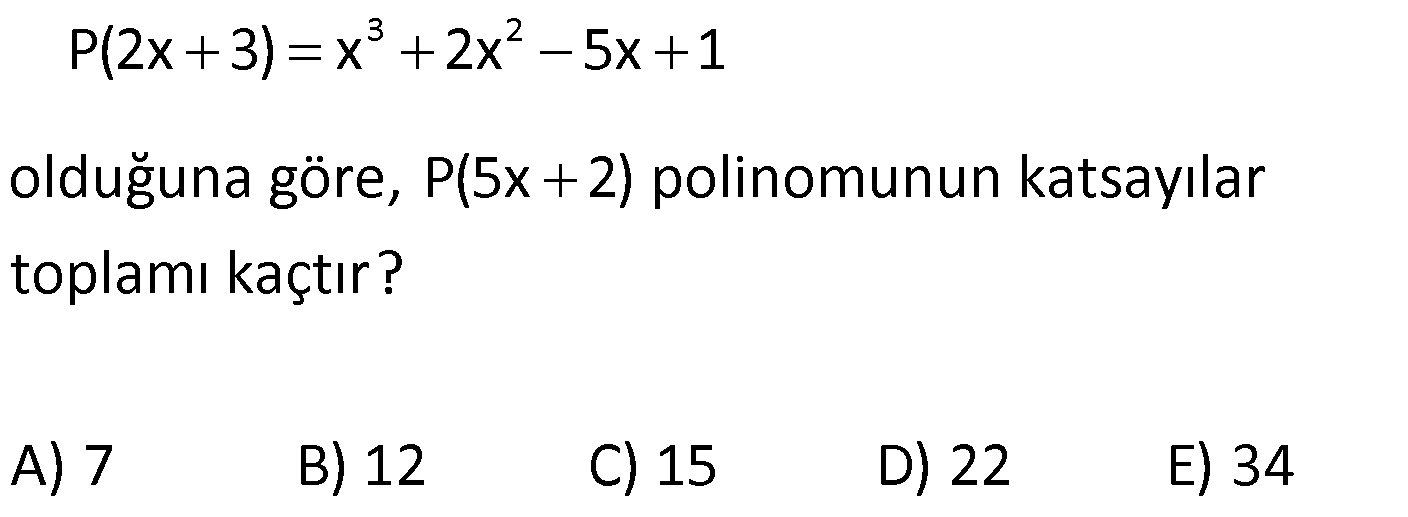
 | | | | |
Çözüm için Tıklayınız.

12.SORU

| | | | | |
Çözüm için Tıklayınız.

13.SORU
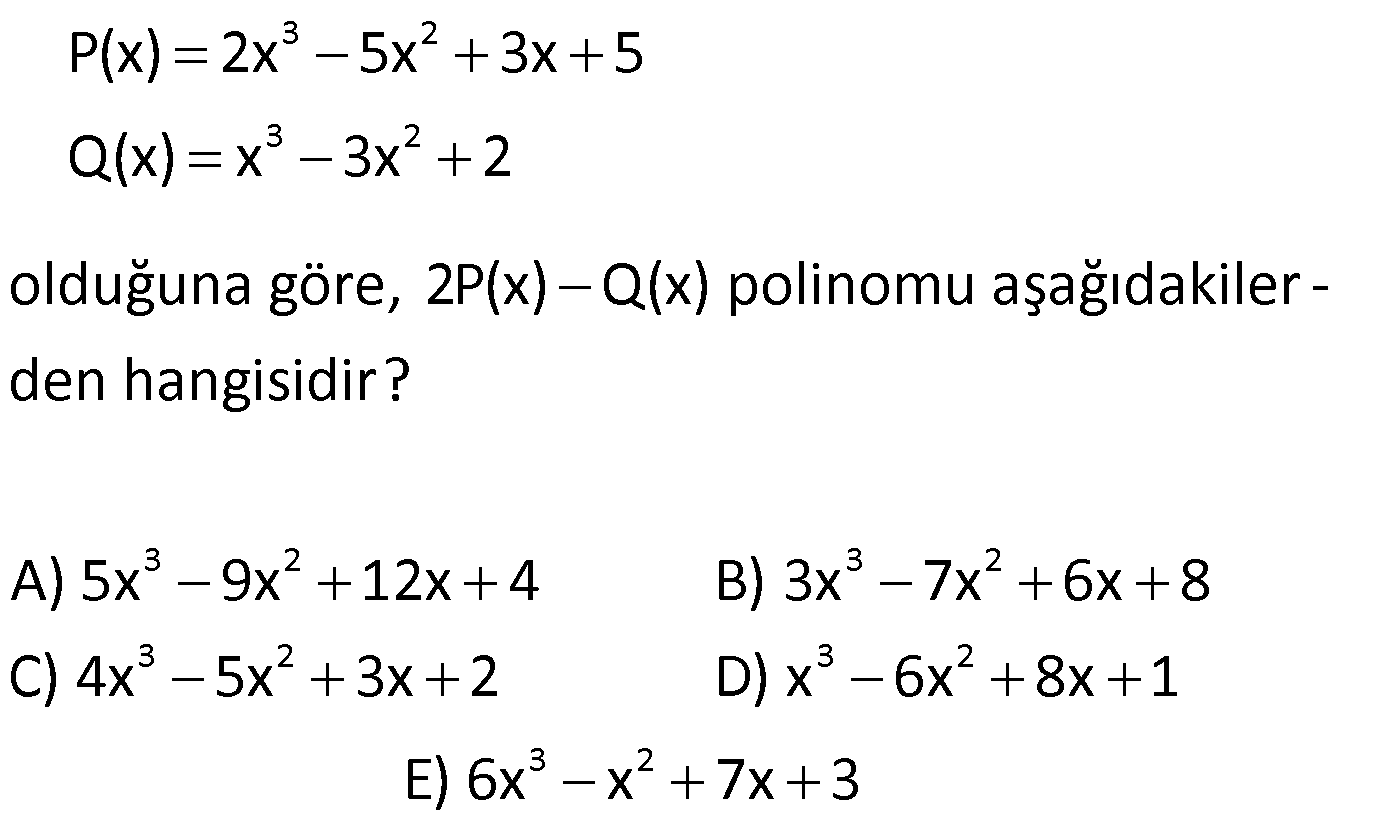
| | | | | |
Çözüm için Tıklayınız.

14.SORU
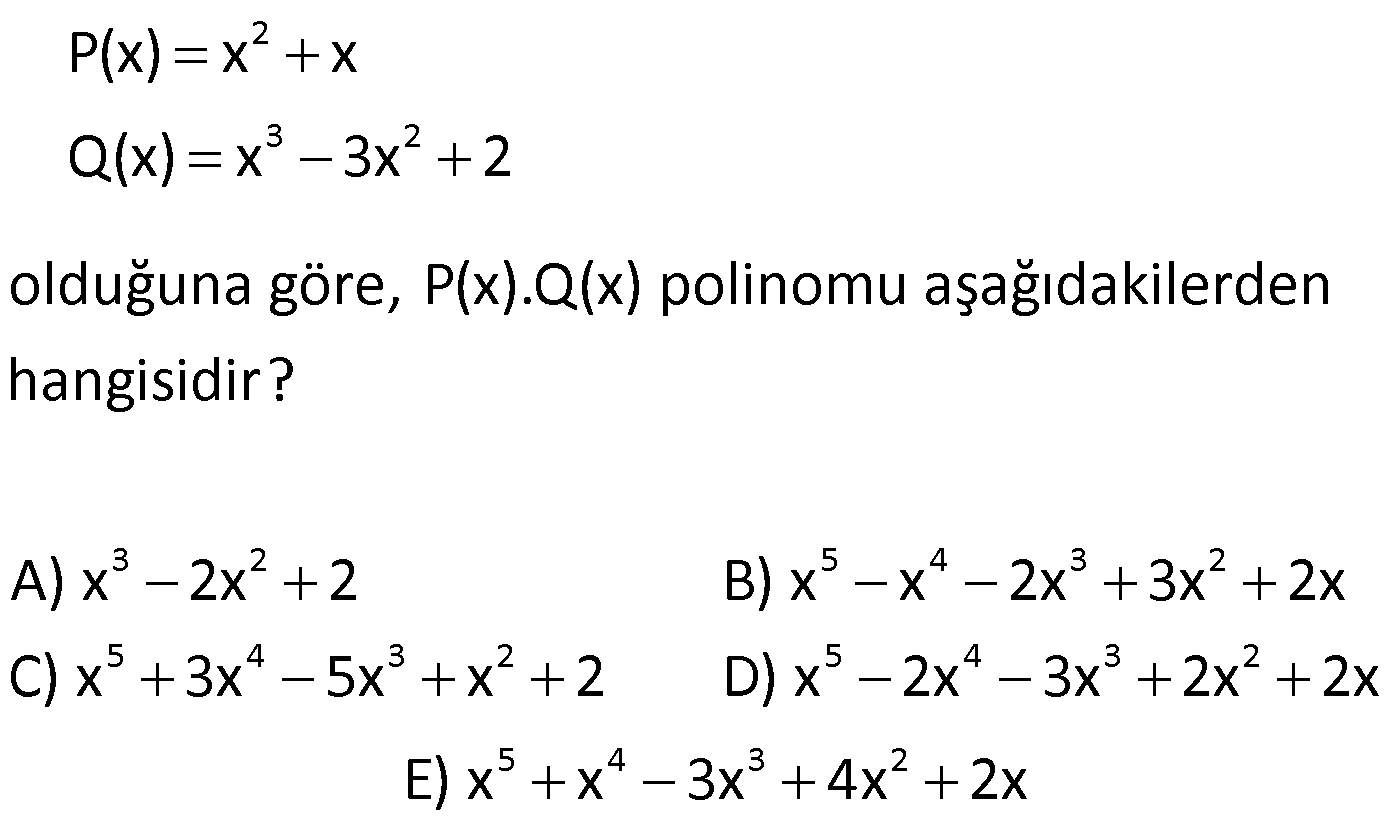
| | | | | |
Çözüm için Tıklayınız.

15.SORU
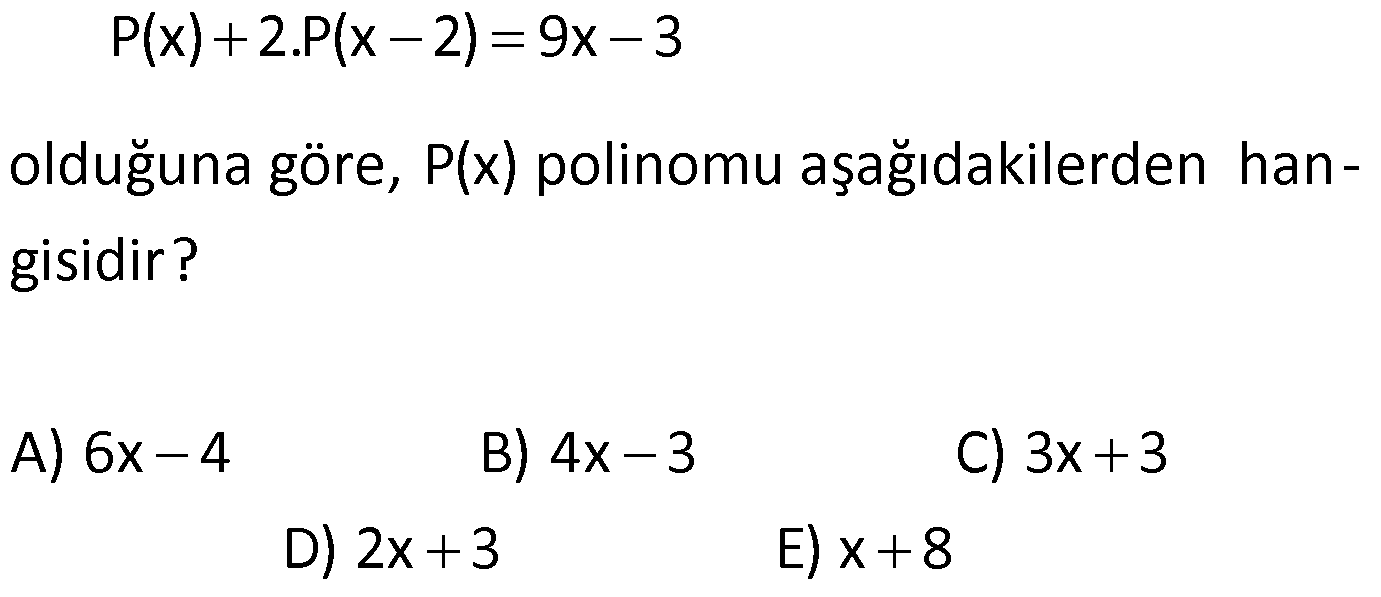
| | | | | |
Çözüm için Tıklayınız.

16.SORU
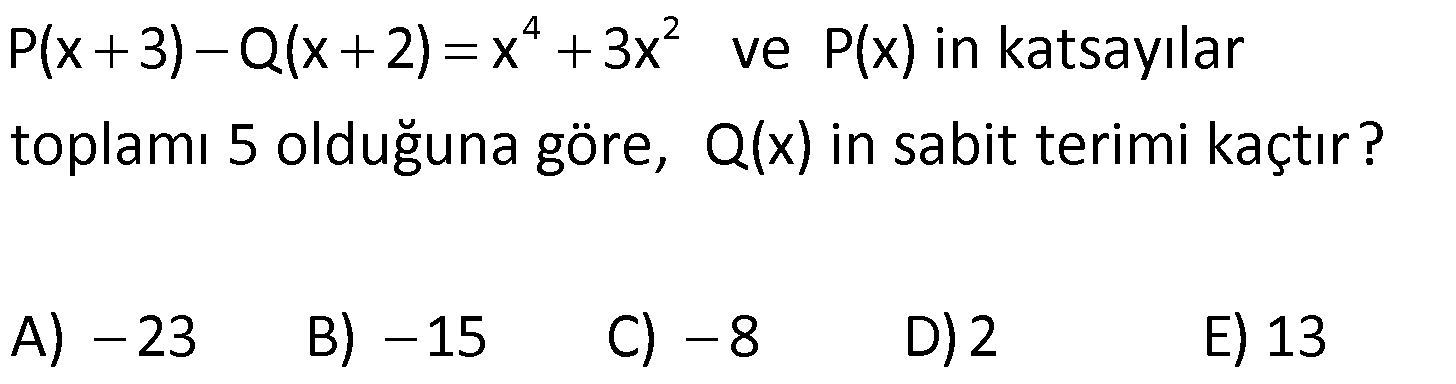
 | | | | |
Çözüm için Tıklayınız.

17.SORU
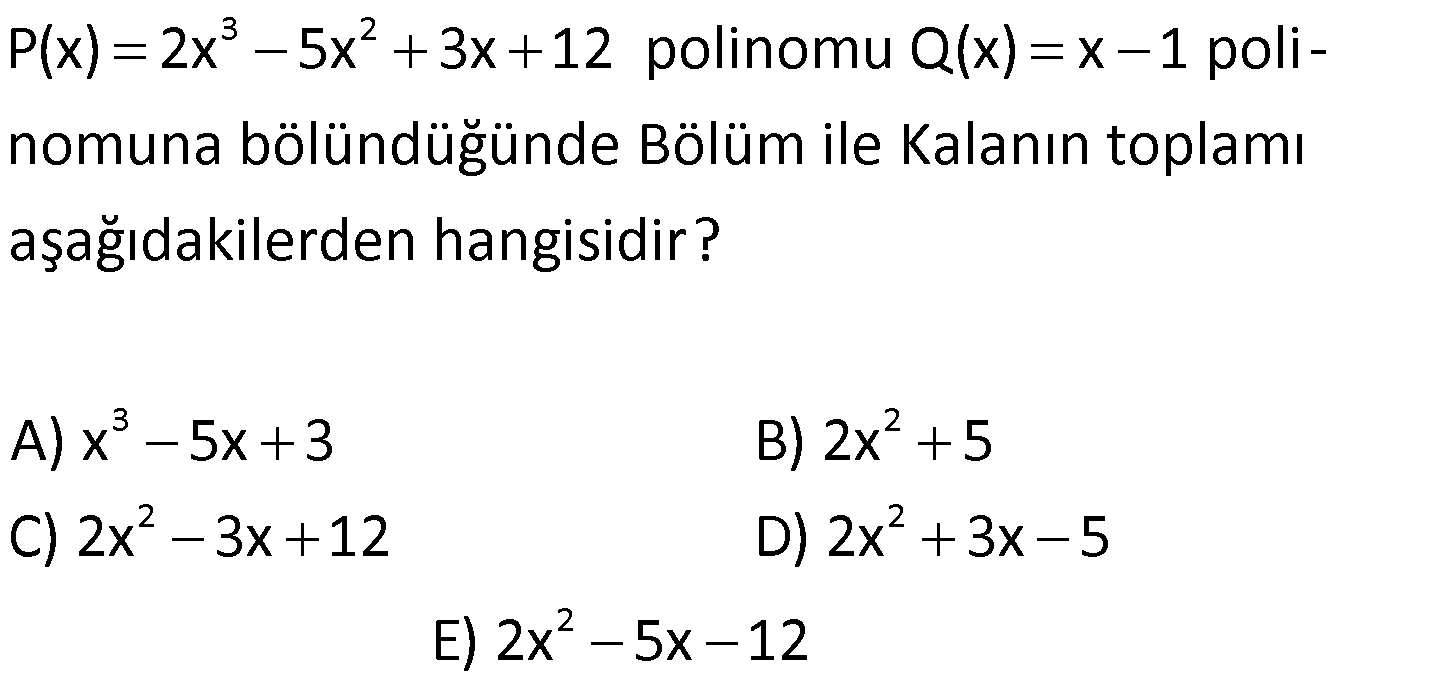
| | | | | |
Çözüm için Tıklayınız.

18.SORU

| | | | | |
Çözüm için Tıklayınız.

19.SORU

| | | | | |
Çözüm için Tıklayınız.

20.SORU
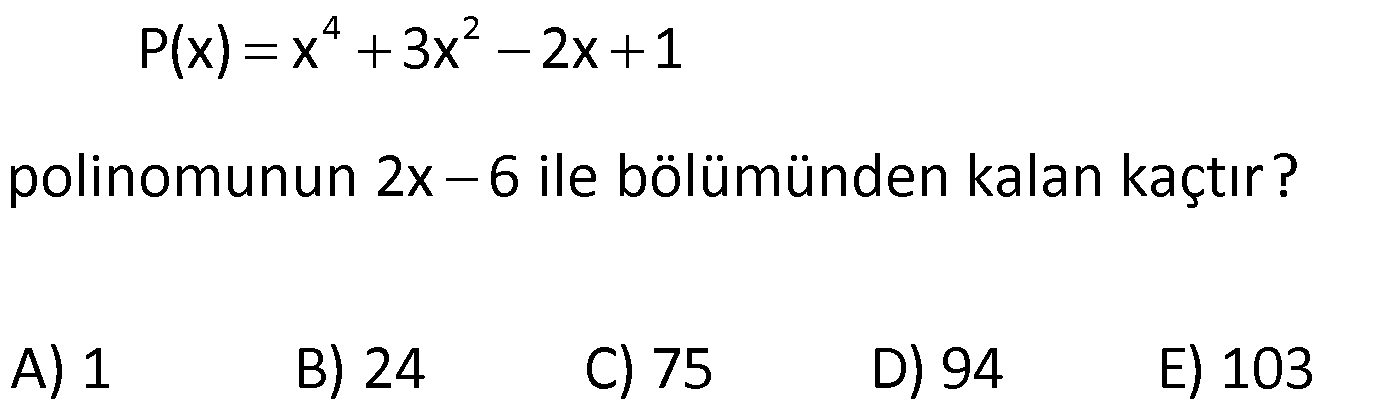
| | | | | |
Çözüm için Tıklayınız.

Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
11) 3 2 P(2x 3) x 2x 5x 1 olduğuna göre, P(5x 2) polinomunun katsayılar toplamı kaçtır? A) 7 B) 12 C) 15 D) 22 E) 34 ÇÖZÜM: 3 2 x 3 yazılarak katsayılar toplamı bulunur. P(5x 2) polinomunun katsayılar toplamı P(5.1 2) P(7) dir. P(7) yi bulmalıyız. P(2x 3) polinomunda x yerine 2 yazarsak, P(7)’yi bulabiliriz. P(2.2 3) 2 2.2 5.2 1 P(7) 8 8 10 1 P(7) 7 dir. Cevap: A 12) 4 P(x) (3x 1) olduğuna göre, P(x) polinomunun çift dereceli terimlerin katsayıları toplamının, tek dereceli terimlerin katsayıları toplamına oranı kaçtır? 23 19 17 13 11 A) B) C) D) E) 18 16 15 12 9 ÇÖZÜM: 4 4 5 4 P(x)’in çift dereceli terimlerin katsayıları toplamı: P(1) P( 1) dir. 2 P(x)’in tek dereceli terimlerin katsayıları toplamı: P(1) P( 1) dir. 2 P(1) (3 1) 2 16 dır. P( 1) ( 3 1) ( 4) 256 dır. B una göre, Çift dereceli terimlerin katsayılar toplamı: 16 256 136 dır. 2 Tek dereceli terimlerin katsayılar toplamı: 16 256 120 dir. 2 136 17 Bunların oranı: tir. 120 15 Cevap: C www.matematikkolay.net 13) 3 2 3 2 3 2 3 2 3 2 3 2 P(x) 2x 5x 3x 5 Q(x) x 3x 2 olduğuna göre, 2P(x) Q(x) polinomu aşağıdakiler – den hangisidir? A) 5x 9x 12x 4 B) 3x 7x 6x 8 C) 4x 5x 3x 2 D) x 6x 8x 1 3 2 E) 6x x 7x 3 ÇÖZÜM: 3 2 3 2 Sabit sayı ile polinom çarpılırken, sabit sayı ile her terimin katsayısı çarpılır. Buna göre, 2P(x) 2(2x 5x 3x 5) 4x 10x 6x 10 dur. Polinomlarda toplama- çıkarma yaparken aynı dere – celi terimlerin ka 3 2 3 2 3 2 tsayıları kendi içinde toplanır ya da çıkarılır. Buna göre, 2P(x) 4x 10x 6x 10 _ Q(x) x 3x 2 2P(x) Q(x) 3x 7x 6x 8 buluruz. Cevap: B 14) 2 3 2 3 2 5 4 3 2 5 4 3 2 5 4 3 2 5 4 3 P(x) x x Q(x) x 3x 2 olduğuna göre, P(x).Q(x) polinomu aşağıdakilerden hangisidir? A) x 2x 2 B) x x 2x 3x 2x C) x 3x 5x x 2 D) x 2x 3x 2x 2x E) x x 3x 4 2 x 2x ÇÖZÜM: 2 3 2 2 3 2 2 2 3 2 5 4 2 4 3 5 4 3 2 P(x)’in her terimi ile Q(x)’in her terimi ayrı ayrı çarpılır. Buna göre, (x x).(x 3x 2) x .x x .( 3x ) x .2 x.x x.( 3x ) x.2 x 3x 2x x 3x 2x x 2x 3x 2x 2x tir. Cevap: D 15) P(x) 2.P(x 2) 9x 3 olduğuna göre, P(x) polinomu aşağıdakilerden hangisidir? A) 6x 4 B) 4x 3 C) 3x 3 D) 2x 3 E) x 8 ÇÖZÜM: 9 olmalı a 3 tür. Toplamdaki ifade 1.dereceden olduğuna göre, P(x) polinomu 1.derece bir polinomdur. P(x) ax b diyebiliriz. Buna göre, ax b 2.(a(x 2) b) 9x 3 ax b 2(ax 2a b) 9x 3 ax b 2ax 4a 2b 9x 3 3a .x 3b 2 olmalı 3 4a 9x 3 3b 4a 3 3b 12 3 3b 9 b 3 tür. O halde, P(x) 3x 3 tür. Cevap: C 16) 4 2 P(x 3) Q(x 2) x 3x ve P(x) in katsayılar toplamı 5 olduğuna göre, Q(x) in sabit terimi kaçtır? A) 23 B) 15 C) 8 D)2 E) 13 ÇÖZÜM: 4 2 P(x) in katsayılar toplamı 5 ise, P(1) 5 tir. Verilen eşitlikte P(1) i kullanabilmek için x 2 yaz – malıyız. P( 2 3) Q( 2 2) ( 2) 3.( 2) P(1) Q(0) 16 12 5 Q(0) 28 Q(0) 23 Q(0) 23 tür. Q(x) in sabit terim i Q(0) dır. O da 23’e eşit. Cevap: A www.matematikkolay.net 17) 3 2 3 2 2 2 P(x) 2x 5x 3x 12 polinomu Q(x) x 1 poli – nomuna bölündüğünde Bölüm ile Kalanın toplamı aşağıdakilerden hangisidir? A) x 5x 3 B) 2x 5 C) 2x 3x 12 D) 2x 3x 5 2 E) 2x 5x 12 ÇÖZÜM: 3 3 2 3 2 Bölme işlemini yapalım. P(x) 2x 5x 3x 12 polinomu Q(x) x 1 poli – nomuna bölündüğünde Bölüm ile Kalanın toplamı aşağıdakilerden hangisidir? 2x 5x 3x 12 x 1 _ 2x 2x 3 2 2 2 2x içinde kaç tane x var 2x 2 3x nin içinde kaç tane x var 3x 2 2 2x 3x 3x 3x 12 _ 3x 3x 12 Bölüm: 2x 3x, Kalan 2 12 Toplarsak 2x 3x 12 olur. Cevap: C 18) 5 3 P(x) ve Q(x) birer polinom olmak üzere, der[x .P (x).Q(x)] 18 ve 2.P(x) der 3 Q(x) olduğuna göre, der[P(x) Q(x)] kaçtır? A) 1 B) 2 C) 3 D) 4 E) 5 ? ? ? ? ? ? ÇÖZÜM: 3 5 3 der[P(x)] a ve der[Q(x)] b olsun. Polinomun üssü alınırsa, derecesi ile çarpılır. der[P (x)] 3a dır. Çarpılan polinomların dereceleri toplanır. der[x .P (x).Q(x)] 18 5 3a b 18 3a b 13 tür. Sabit sayı ile çarpım, polinomun derecesini değiş – tirmez. der[2.P(x)] a dır. Bölmede polinomların derecesi çıkarılır. 2.P(x) der 3 ise a b 3 tür. Q(x) 3a b 13 idi. ? ? ? ? ? ? 4 4a 16 a 4 tür. a b 3 b 1 dir. Toplama ya da çıkarmada derecesi büyük olan polinomun derecesi geçerlidir. der[P(x) Q(x)] 4 tür. Cevap: D 19) 2 3 3 P(x) ve Q(x) birer polinom olmak üzere, der[P(x 1).x )] 13 ve der Q(x ) P(x) 6 olduğuna göre, der[P(x).Q(x)] kaçtır? A) 6 B) 7 C) 8 D) 9 E) 10 ?? ?? ÇÖZÜM: 2 3 3 der[P(x)] a ve der[Q(x)] b olsun. der[P(x 1).x )] 13 ise 2a 3 13 2a 10 a 5 tir. der Q(x ) P(x) 6 ise P(x) in derecesi 5 ?? ?? 3 olduğuna göre, Q(x ) ün derecesi 6 olmalıdır. 3b 6 b 2 dir. der[P(x).Q(x)] a b 5 2 7 dir. Cevap: B 20) 4 2 P(x) x 3x 2x 1 polinomunun 2x 6 ile bölümünden kalan kaçtır? A) 1 B) 24 C) 75 D) 94 E) 103 ÇÖZÜM: 4 2 Böleni 0’a eşitleyelim. 2x 6 0 x 3 tür. x’in yerine 3 yazarak kalanı bulabiliriz. P(3) 3 3.3 2.3 1 81 27 6 1 103 tür. Cevap: E www.matematikkolay.net



13. sorunun çözümündeki çıkarma işleminde, -10x(2) (-) -3x(2) nin sonucu -7x(2) değil, -13x(2) olmalı
Hayır, çözümdeki işlem doğru. İki (-) yan yana gelince (+) ya dönüşecektir.
1. soruda 3 den büyük 4 de var 4ü niye almadınız ???
m=4 olursa 16/(m+2) ifadesi 16/6 olur. Yani doğal sayı olmayan bir ifade olur. Ama, polinomlarda x’in üssü doğal sayı olmalıydı. O yüzden alamayız.
2.sorunun çözümünde hata var.X li terimi yok etmemiz için b=-9 olmalı ki -4x ile +4x birbirini götürsün.
Uyarınınz için teşekkürler. Yazım hatası yazılmış. (b+5)x yerine (b+1)x olacaktı. Düzeltildi.
19.soruda p[x’in karesile x’in küpünü çarpmamız gerekmez mi x küpü içeri dağıtıp ona göre açmamız gerekmez mi ?
Hayır gerekmiyor. Soruda bir parantez fazla kalmış. Belki o sizi yanıltmış olabilir. Şimdi kaldırdık.
12.soruda p(-3-1)’in üssü 4 olması gerekiyor değil mi 5 yazmışsınız 😊
Uyarınız için teşekkürler. Yazım hatası düzeltildi.
Sorulariniz efsane guzel olmus bu kadar bildigimi bilmiyodum😁ellerinize emegnize saglik
teşekkürler sorular için 🙂
🙂
Bunlar 10. Sınıf için dimi
Evet.
Aynı zamanda TYT-AYT konusu
siteniz çok güzel ✨. sorular için teşekkür ederim 👍
bana 100 adet soru lazım bu konuyla ilgili nereden blabilirim ?
12. soruda cevap -15/30 olması gerekmez mi
İnceledik ama hata göremedik.
Sorular o kadar güzel ve cevaplar o kadar özenle hazırlanmışki anlatacak birine ihtiyaç almıyor emeğinize sağlık. Fakat sorular daha çok olmalı diye düşünüyorum
Sorularda şuanda hata var mı?
Yani yanlış denilen yerler soruda düzeltilmiş miydi?
Hata belirtildiği an sorular hemen inceleniyor ve düzeltiliyor. Dolayısıyla şu anda düzeltilmiş hallerini görüyorsunuz.
15. Soruda 3b-4a ifadesine -2 olmalı denmiş altına orda -3 olması gerekiyor
Uyarınız için teşekkürler. Yazım hatası düzeltildi.