11.SORU

| | | | | |
Çözüm için Tıklayınız.

12.SORU

 | | | | |
Çözüm için Tıklayınız.

13.SORU

| | | | | |
Çözüm için Tıklayınız.

14.SORU

| | | | | |
Çözüm için Tıklayınız.

15.SORU
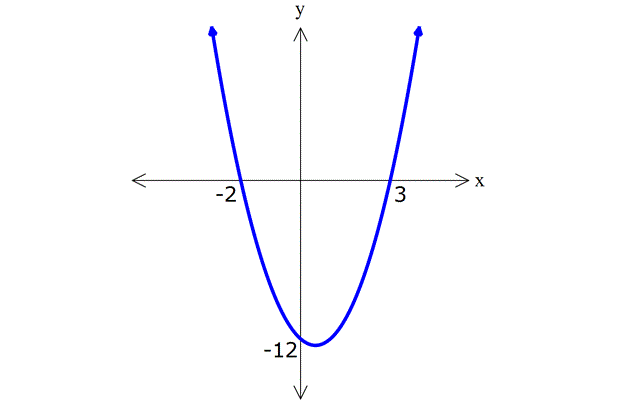

 | | | | |
Çözüm için Tıklayınız.

16.SORU
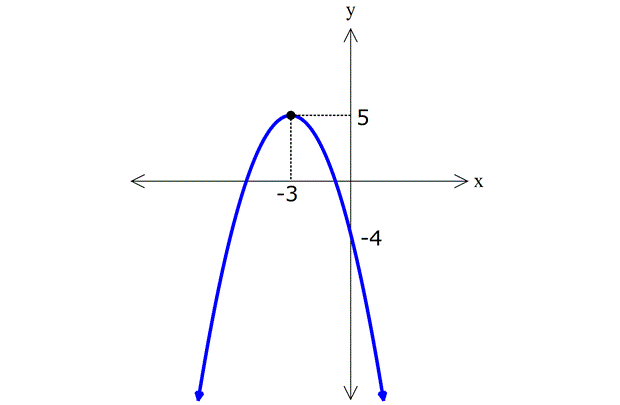

| | | | | |
Çözüm için Tıklayınız.

17.SORU

| | | | | |
Çözüm için Tıklayınız.

18.SORU
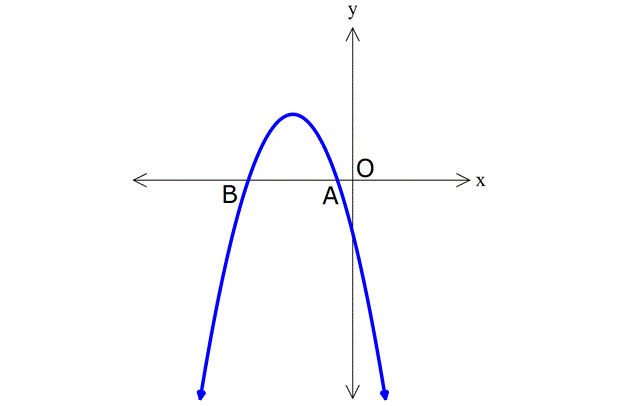

| | | | | |
Çözüm için Tıklayınız.

19.SORU
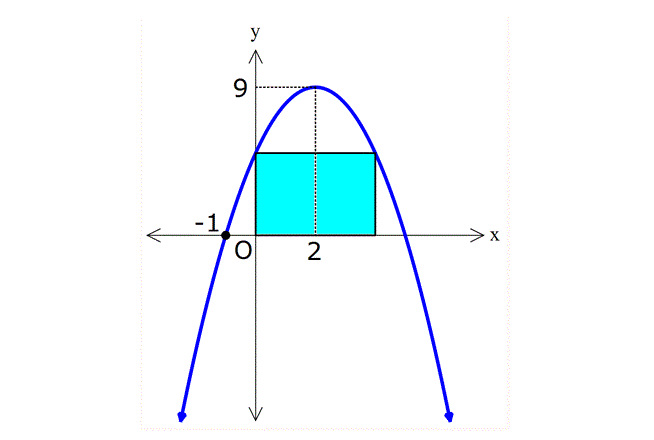

| | | | | |
Çözüm için Tıklayınız.

20.SORU

| | | | | |
Çözüm için Tıklayınız.

Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
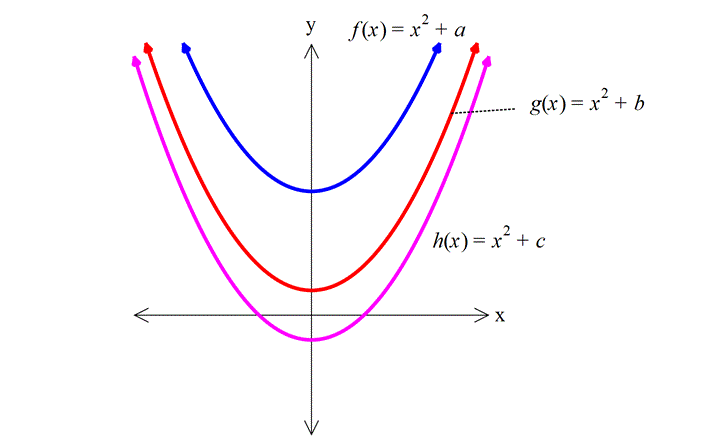
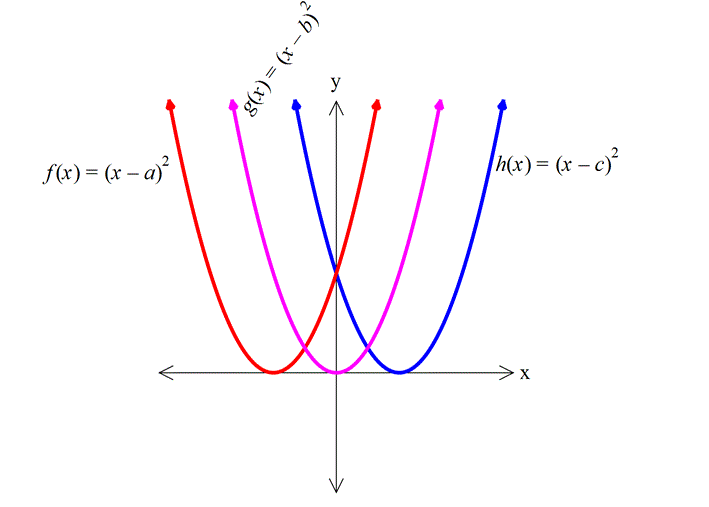
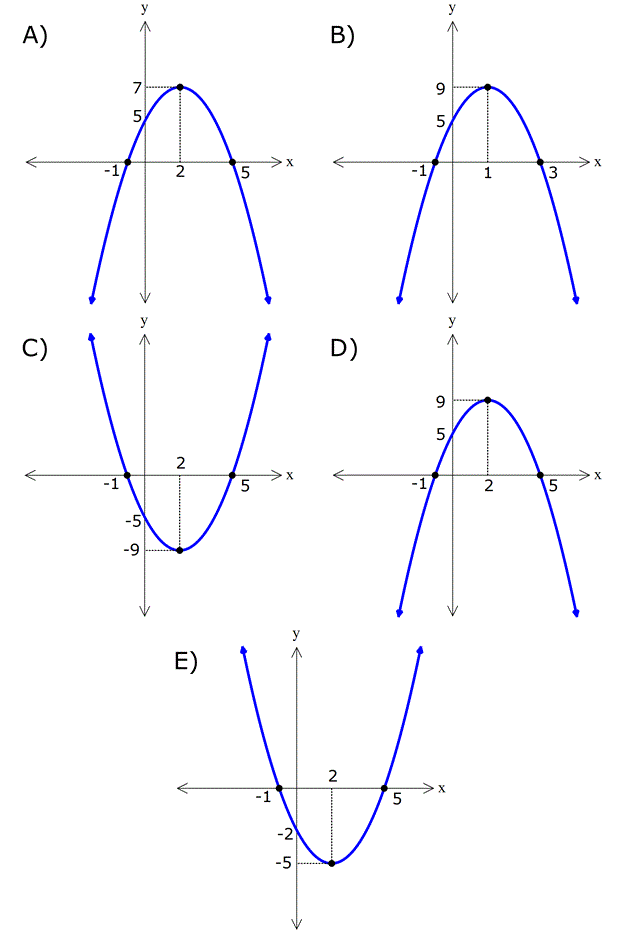
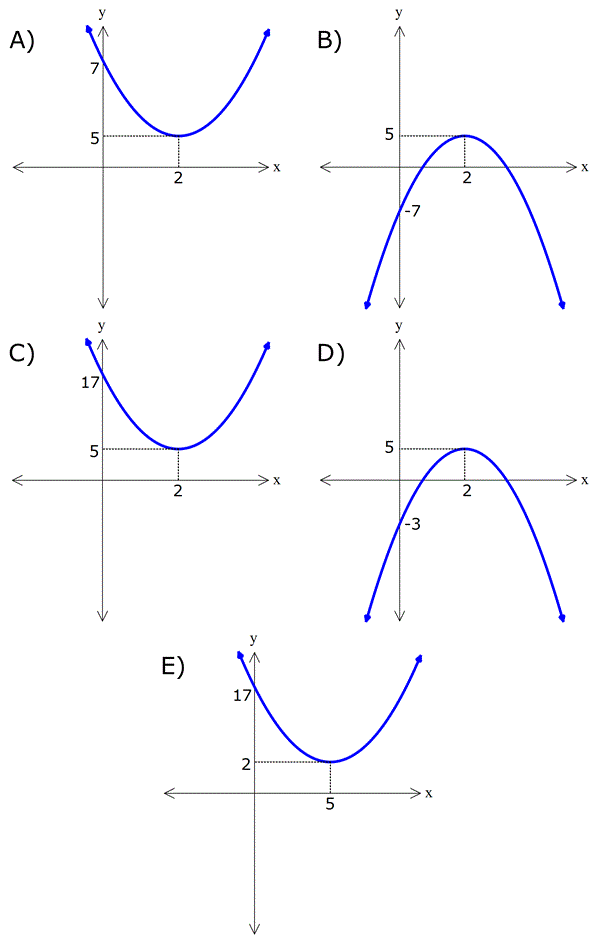
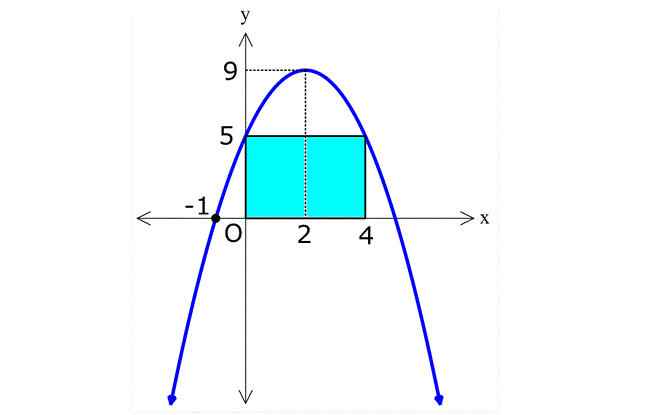
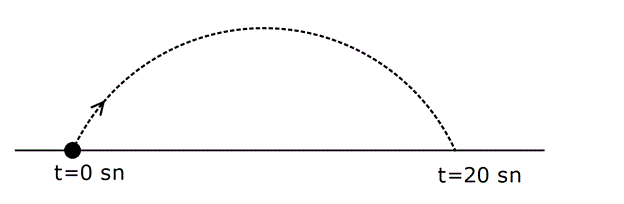
11) Yukarıdaki grafikleri verilen f, g ve h fonksiyonlarına göre, a,b ve c değerlerinin sıralaması hangi şıkta doğru gösterilmiştir? A) a b c B) c a b C) c b a D) a c b E) b a c ÇÖZÜM: 2 ax bx c parabolünde c değeri ne kadar yüksekse y eksenini o kadar daha yüksek yerden keser. Çünkü f(0) c dir. Buna göre, f, g ve h parabolleri için c b a dır, diyebiliriz. Cevap : C 12) Yukarıdaki grafikleri verilen f, g ve h fonksiyonlarına göre, a,b ve c değerlerinin sıralaması hangi şıkta doğru gösterilmiştir? A) a b c B) c a b C) c b a D) a c b E) b a c www.matematikkolay.net ÇÖZÜM: 2 a(x k) şeklindeki parabollerde k değeri arttıkça parabol sağa doğru kayar. Çünkü parabolü 0 yapan x değeri artar. Buna göre, f, g ve h parabolleri için, a b c dir, diyebiliriz. Cevap: A 13) 2 f(x) x 4x 5 fonksiyonunun grafiği aşağıdakilerden hangisidir? ÇÖZÜM: 2 2 x 5 x 1 x nin katsayısı negatif olduğundan parabolün kol – ları aşağı doğru olacaktır. C ve E şıkları elenir. x eksenini kestiği noktaları bulalım. x 4x 5 0 ( x 5)(x 1) 0 x 5 ve x 1 de keser. B şıkkı da elendi. 2 2 y eksenini kestiği noktayı bulalım. f(0) 0 4.0 5 5 tir. Şimdi tepe noktasının apsisini bulalım. b 4 r 2 dir. Ordinatını bulalım. 2a 2 f(2) 2 4.2 5 4 8 5 9 dur. A şıkkı elendi. Cevap: D 14) 2 f(x) 3(x 2) 5 fonksiyonunun grafiği aşağıdakilerden hangisidir? ÇÖZÜM: 2 2 Tepe noktası T(r, k) olan bir parabolün denklemi f(x) a(x r) k şeklindedir. Dolayısıyla f(x) 3(x 2) 5 fonksiyonunun tepe noktası (2, 5) noktasıdır. E şıkkı elenir. a 0 olduğundan kolları yukarı y 2 önlüdür. B ve D şıkları da elendi. y eksenini nerde keser, bulalım. f(0) 3(0 2) 5 12 5 17’de keser. Cevap: C www.matematikkolay.net 15) 2 2 2 2 2 Yukarıda grafiği verilen parabolün denklemi aşağı – dakilerden hangisinde doğru verilmiştir? A) y 2x 12x 12 B) y x 6x 12 C) y 3x 12x 6 D) y x 4x 8 E) y 2x 12x 12 ÇÖZÜM: Parabolün x eksenini kestiği yerler 2 ve 3 ise y a(x 2)(x 3) şeklinde bir denkleme sahiptir. x 0 için y eksenini 12 de kesiyorsa, 12 a(0 2)(0 3) 12 6a a 2 dir. O halde parabolün denklemi y 2(x 2)(x 2 2 3) 2(x x 6) 2x 2x 12 dir. Cevap: A 16) 2 2 2 2 2 Yukarıda grafiği verilen parabolün denklemi aşağı – dakilerden hangisinde doğru verilmiştir? A) y x 12x 4 B) y 2x 3x 4 C) y x 3x 4 D) y x 9x 4 E) y x 6x 4 ÇÖZÜM: 2 2 Tepe noktası T(r, k) olan bir parabolün denklemi f(x) a(x r) k şeklindedir. Dolayısıyla yukarıdaki parabolün denklemi y a(x 3) 5 şeklindedir. y eksenini kestiği yerden de a’ yı bulalım. x 0 için y 2 2 2 2 2 4 olmalıdır. 4 a(0 3) 5 4 9a 5 9 9a a 1 dir. y (x 3) 5 (x 6x 9) 5 x 6x 9 5 x 6x 4 tür. Cevap: E 17) 2 2 2 2 A(0, 5), B(1, 3) ve C(3, 11) noktalarından geçen parabolün denklemi aşağıdakilerden hangisidir? A) y x 4x 5 B) y 2x 4x 5 C) y 2x 3x 5 D) y x 6x 5 E) y 2 x 4x 5 ÇÖZÜM: 2 2 2 Parabolün denklemi y ax bx c olsun. 3 nokta ile, a,b ve c’yi bulabiliriz. A(0, 5) noktası x 0 için y 5 olmalı 5 a.0 b.0 c c 5 tir. B(1, 3) noktası x 1 için y 3 olmalı 3 a.1 b.1 2 5 a b 2 dir. C(3, 11) noktası x 3 için y 11 olmalı 11 a.3 b.3 5 11 9a 3b 5 6 9a 3b (3’e böl.) 2 3a b 2 2 dir. a b 2 _ 3a b 2 taraf tarafa çıkaralım. 2a 4 a 2 dir. a b 2 b 4 tür. Buna göre, y 2x 4x 5 tir. Cevap: B www.matematikkolay.net 18) 2 Yukarıda grafiği verilen parabolün denklemi y x 5x k dır. AB 3. OA olduğuna göre, k kaçtır? A) 1 B) 2 C) 3 D) 4 E) 5 ÇÖZÜM: AO m olsun. AB 3m olur. A noktasının koordinatı ( m, 0) B noktasının koordinatı ise ( 4m, 0) olur. İkisinin orta noktası, tepe noktasının apsisidir. m 4m 5m r dir. 2 2 b 5m 5 r olduğundan 2a 2 2 2 m 1 dir. A noktasını kullanalım. ( 1, 0) noktasıdır. Parabolün denklemini sağlayacaktır. 0 1 5 1 k 0 1 5 k 0 4 k k 4 tür. Cevap: D 19) Yukarıda grafiği verilen parabolün tepe noktası T(2, 9) olduğuna göre, taralı dikdörtgenin alanı kaç birimkaredir? A) 10 B) 15 C) 20 D) 25 E) 30 ÇÖZÜM: 2 2 2 y a(x 2) 9 şeklinde bir denkleme sahiptir. ( 1, 0) noktasını da kullanalım. 0 a( 1 2) 9 0 a.9 9 9 9a a 1 dir. y (x 2) 9 parabolü y ekse 2 2 nini nerde kesiyor, bulalım. x 0 için y 0 2 9 5 tir. O halde, dikdörtgenin bir kenarı 5 birimdir. Parabolün simetri ekseni x 2 doğrusu olduğundan, dikdörtgenin diğer kenarı 2 2 4 br olur. Alan 5.4 20 br olur. Cevap: C 20) 2 Yukarıdaki gibi bir top, eğik olarak hareket ediyor. Topun yerden yüksekliği zamana (t : saniye) bağlı t olarak h 5t olarak ifade ediliyor. 4 Buna göre, top havada kaç saniye kalır? A) 10 B) 15 C) 20 D) 25 E) 30 ÇÖZÜM: 2 2 h 0 olduğunda top yerdedir. t 0 5t 4 ile genişletelim. 4 0 t 20t 0 t( t 20) t 0 ve t 20 de h 0 dır. O halde bu hareket 20 saniye sürmektedir. Cevap: C www.matematikkolay.net


Gerçekten çok yararlı ve güzel bir site ellerinize sağlık…
berbat berbat berbat
Çok teşekkür ederim çok güzel bir sayfa olmuş
15. soruda A şıkkını yanlış yazmışsınız cevapla örtüşmüyor.
Uyarınız için teşekkürler. Yazım hatası yapılmış. Düzeltildi.
Çok güzel çok yararlı sorular hazırlamışsınız emeğinize sağlık
13. sorunun cevabı hatalı cunku parabolun kolları asagı doğru olmalı cevabın b olması gerekiyor
sorularınız güzel ve kaliteli
Eksenleri kestiği noktalara ve tepe noktasına da bakmalısın. Kolları aşağı doğru olan başka şıklar da var.
21. Sorunun cevabinda 11a yazilcagina 12 a yazilmis
a ile 2a^2+11a-3 ifadesi toplanıyor. Bu nedenle 11a olan kısım 12a ‘ya çıkıyor. Burayı kastediyorsanız, burda bir hata yok.
16. Soruda e şıkkında sabit sayının 14 olması gerekmiyor mu ?
Hayır. x e 0 vererek test edebilirsiniz. y eksenini -4 te kesmesi lazım.
Teşekkür ederim
hocam parabol testinin cevap anahtarı var mıdır? Şimdiden teşekkürler.
Maalesef, hazır liste olarak koymamışız. Çözümlerin altına bakarak kontrol edebilirsiniz.
Çok güzel hazırlamışsınız.Ellerinize sağlık hocam.
Aşırı güzel sorular temel attırmalık :))♡♡ teşekkürler.
Soru 6 nın çözümü hatalı -2’nin karesi -4 olarak yazılmış
-(2 nin karesi)=-4 tür. (-2)^2=4 ile karıştırmayınız.
Soru 13 te -4/2.-1 in cevabı -2 bulunması lazımdı ve fonksiyonda yerine yazıldığı zaman -2 nin karesi -4 değil +4 olması gerekirdi
13.soruyu kontrol ettik ama hata göremedik.
bu soruların hangi yıllar olduğunu söyleyebilir msiniz
Bu sorular çıkmış sorular değil. Telif hakkı nedeniyle çıkmış soruları kullanamıyoruz.