Parabol

Bu bölümde Parabol ile ilgili 26 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…

 

1.SORU

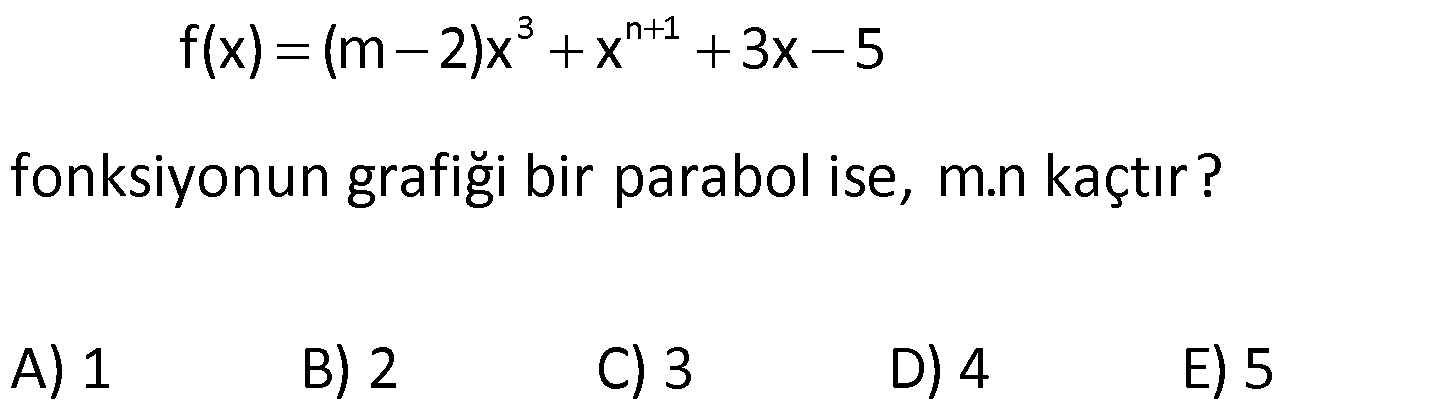
Çözüm için Tıklayınız.


2.SORU

Çözüm için Tıklayınız.

3.SORU

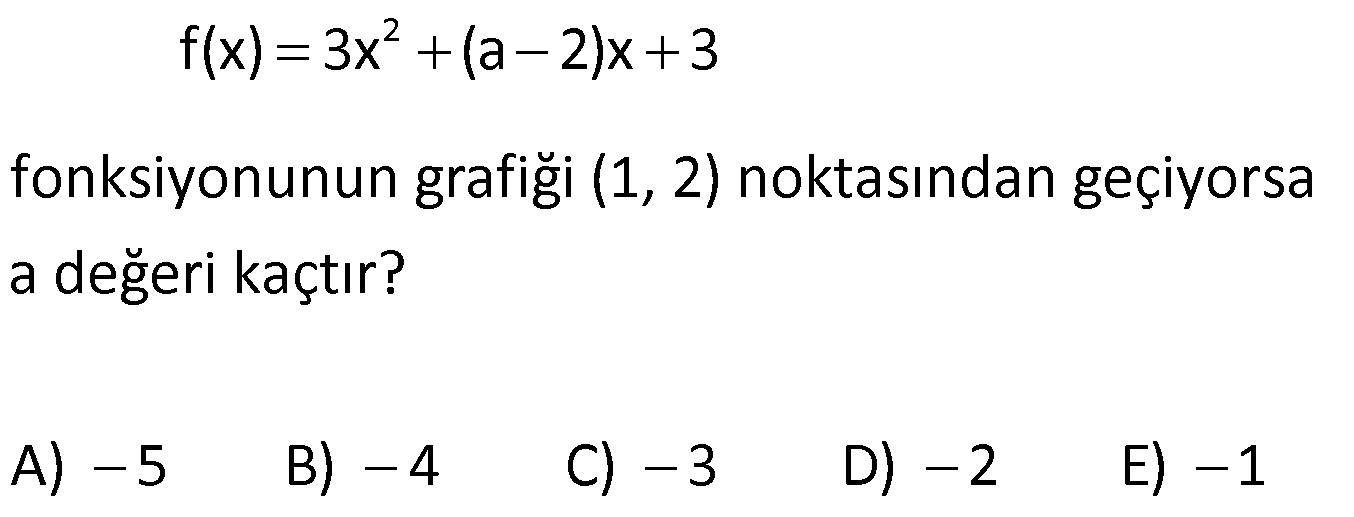
Çözüm için Tıklayınız.

4.SORU

Çözüm için Tıklayınız.

5.SORU

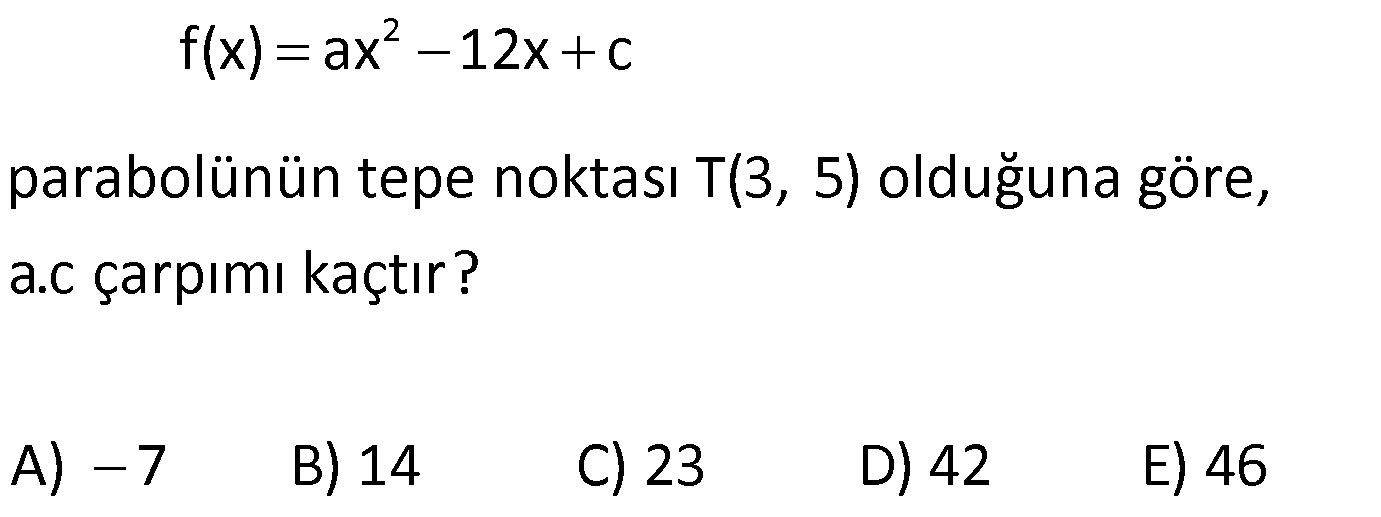
Çözüm için Tıklayınız.

6.SORU

Çözüm için Tıklayınız.

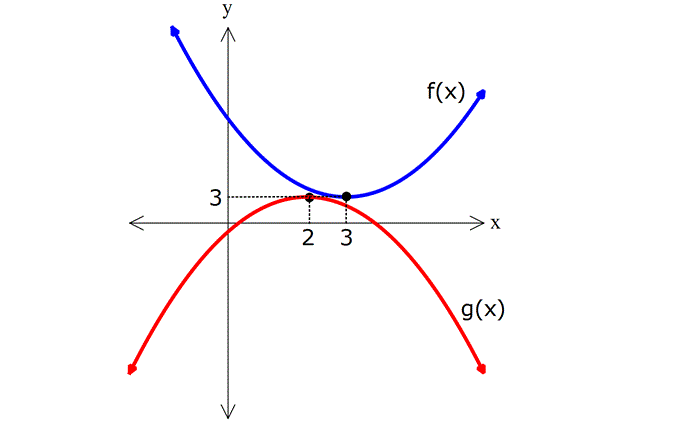
7.SORU

Çözüm için Tıklayınız.

8.SORU

Çözüm için Tıklayınız.

9.SORU

Çözüm için Tıklayınız.

10.SORU

Çözüm için Tıklayınız.

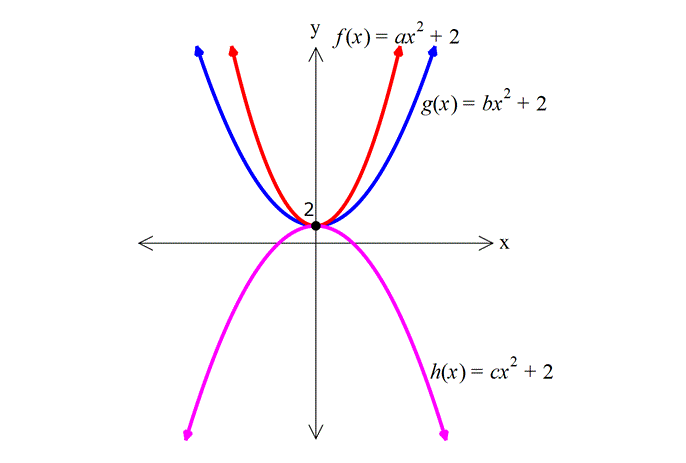
2.Sayfa için Tıklayınız.

Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.

 

Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)

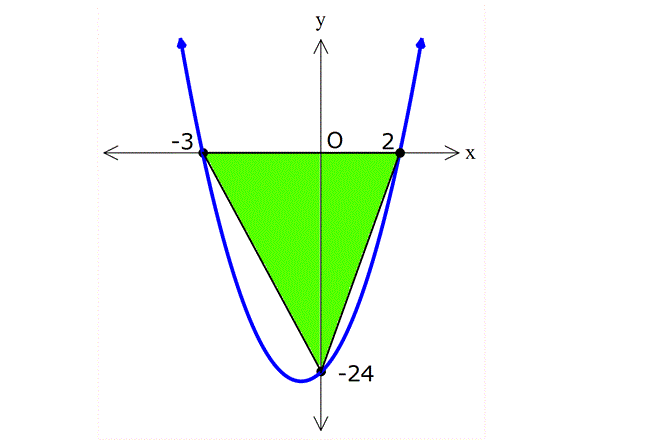
PARABOL TESTİ www.matematikkolay.net 1) 3 n 1 f(x) (m 2)x x 3x 5 fonksiyonun grafiği bir parabol ise, m.n kaçtır? A) 1 B) 2 C) 3 D) 4 E) 5 ÇÖZÜM: 3 2 Parabol olması için, ikinci dereceden bir fonksiyon olmalıdır. Dolayısıyla x lü terimin katsayısı 0 olmalıdır. m 2 0 m 2 dir. x li bir terim olması için de n 1 2 n 1 olmalıdır. m.n 2.1 2 buluruz. Ce vap: B 2) 2 f(x) (m 3)x 5x 2 parabolünün kolları yukarı doğru ise, m’nin değer aralığı aşağıdakilerden hangisidir? A) (3, ) B) (5, ) C) (3, 5) D) (0, 3) E) (0, 5)   ÇÖZÜM: 2 x li terimin katsayısı pozitif olmalıdır. Yani m 3 0 m 3 tür. O halde, m (3, ) aralığıdır. Cevap: A     3) 2 f(x) 3x (a 2)x 3 fonksiyonunun grafiği (1, 2) noktasından geçiyorsa a değeri kaçtır? A) 5 B) 4 C) 3 D) 2 E) 1 ÇÖZÜM: 2 (1, 2) noktası, grafiğin denklemini sağlamalıdır. f(1) 2 dir. 3.1 (a 2).1 3 2 3 a 2 3 2 4 a 2 a 2 dir. Cevap: D 4) 2 2 f(x) ax 4x 24 parabolünün x ekseninin kestiği noktaların apsisleri toplamı 1 olduğuna göre, parabolün eksenleri kestiği noktaları köşe kabul eden üçgenin alanı kaç br dir? A) 30 B) 45 C) 60 D) 90 E) 120 ÇÖZÜM: 2 x eksenini kestiği yerler f(x) 0 denkleminin kökleri – b dir. Kökler toplamı formülü ile bulunduğundan, a 4 1 olmalıdır. a 4 tür. a O halde, f(x) 4x 4x 24 parabolünün eksenleri kestiği nok – taları bu 2 2 02.Mar 2 lalım. 4x 4x 24 0 4 ile sadeleştirelim. x x 6 0 (x 2)(x 3) 0 x 2 ve x 3 te x eksenini keser. y eksenini kestiği nokta için x 0 yazarız. f(0) 4.0 4.0 24 24 te y eksenini keser. www.matematikkolay.net 2 Üçgenin tabanı 5 br, yüksekliği 24 br olur. May.24 Alan 60 br dir. 2 Cevap: C 5) 2 f(x) ax 12x c parabolünün tepe noktası T(3, 5) olduğuna göre, a.c çarpımı kaçtır? A) 7 B) 14 C) 23 D) 42 E) 46 ÇÖZÜM: 2 2 b Parabolün tepe noktasının apsisi formülü ile 2a bulunur. 12 3 ise a 2 dir. 2a f(x) 2x 12x c dir. Tepe noktasının ordinatı da f(3) tür. f(3) 5 ise, 2.3 12.3 c 5 18 36 c 5 18 c 5 c 23 tür. a.c 2.23 46 buluruz. Cevap: E 6) 2 2 f(x) x 6x 12 g(x) x 4x k olmak üzere, f(x)’in en küçük değeri, g(x)’in en büyük değerine eşit olduğuna göre, k kaçtır? A) 5 B) 3 C) 2 D) 1 E) 1 ÇÖZÜM: 2 b 6 f(x)’in tepe noktasının apsisi 3 tür. 2a 2.1 En küçük değeri f(3) 3 6.3 12 9 18 12 3 tür. Demek ki g(x) in en büyük değeri 3 müş. İlk önce tepe noktasının apsisini bulalım. ÇÖZÜM: 2 b 4 r 2 dir. O halde, 2a 2.( 1) g(2) 3 olmalıdır. 2 4.2 k 3 4 8 k 3 4 k 3 k 1 dir. Cevap: D (Görsel olarak bu durum, aşağıda verilmiştir.) 7) 2 f(x) x mx m 3 parabolünün simetri ekseni x 5 doğrusu olduğuna göre, parabolün y eksenini kestiği nok tanın ordinatı kaçtır? A) 8 B) 13 C) 16 D) 20 E) 23 ÇÖZÜM: 2 b Parabolün simetri ekseni x doğrusudur. 2a m Buna göre, 5 m 10 dur. O halde, 2 f(x) x 10x 13 tür. y eksenini kestiği yer f(0) 13 tür. Cevap: B 8) 2 f(x) x 3x m parabolünün tepe noktası x ekseni üzerinde ise m kaçtır? 3 3 9 9 A) 3 B) C) D) E) 2 4 4 2 www.matematikkolay.net ÇÖZÜM: 2 2 Tepe noktası x ekseni üzerinde ise, parabol x ekseni – ne teğettir. Bu durumda 0 olmalıdır. b 4ac 0 3 4.( 1).( m) 0 9 4m 0 9 m tür. Cevap: D 4  9) 2 f(x) mx 5x 3 fonksiyonu daima pozitif değerler alıyorsa, m’nin en küçük tam sayı değeri kaçtır? A) 1 B) 2 C) 3 D) 4 E) 5 ÇÖZÜM: 2 Fonksiyon daima pozitif ise, hiç bir zaman x eksenini kesmiyordur. O halde, 0 olmalıdır. b 4ac 0 25 4.m.3 0 25 12m 0 12m 25 25 12m 25 m m’nin tam sayı değeri 12    en az 3 tür. Cevap: C 10) Yukarıdaki grafikleri verilen f, g ve h fonksiyonlarına göre, a,b ve c değerlerinin sıralaması hangi şıkta doğru gösterilmiştir? A) a b c B) c a b C) c b a D) a c b E) b a c ÇÖZÜM: 2 h parabolünün kolları aşağı yönlü olduğundan c 0 dır. Dolayısıyla en küçük c dir. x nin katsayısı arttıkça kollar arası genişlik azalır. Çünkü aynı x değeri için artık fonksiyon daha büyük değerler alır . Bu sebeple b a dır. O halde, c b a dır. Cevap : C

Sayfalar: 1 2 3

“Parabol” üzerine 23 yorum

  6. 13. sorunun cevabı hatalı cunku parabolun kolları asagı doğru olmalı cevabın b olması gerekiyor

    sorularınız güzel ve kaliteli

    • Eksenleri kestiği noktalara ve tepe noktasına da bakmalısın. Kolları aşağı doğru olan başka şıklar da var.

    • a ile 2a^2+11a-3 ifadesi toplanıyor. Bu nedenle 11a olan kısım 12a ‘ya çıkıyor. Burayı kastediyorsanız, burda bir hata yok.

    • Maalesef, hazır liste olarak koymamışız. Çözümlerin altına bakarak kontrol edebilirsiniz.

  13. Soru 13 te -4/2.-1 in cevabı -2 bulunması lazımdı ve fonksiyonda yerine yazıldığı zaman -2 nin karesi -4 değil +4 olması gerekirdi

    • Bu sorular çıkmış sorular değil. Telif hakkı nedeniyle çıkmış soruları kullanamıyoruz.

Yorum yapın