Mutlak Değer (Latex Formatı)

Bu bölümde Mutlak Değer ile ilgili 22 adet soru bulunmaktadır. Sorularınızı çözdükten sonra “Doğru Cevap” seçeneğine tıklayarak doğru şıkkı görebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. Sorular Latex formatında hazırlanarak görünüm iyileştirilmiştir. İyi Çalışmalar…


SORULAR

SORU 1


|6 – 2| + |2 – 5| – |1 + 4|
işleminin sonucu kaçtır?

A) 2    B) 2     C) 5     D) 7      E) 12

Doğru Cevap Çözüm için Tıklayınız

SORU 2

x < 0 < y < z olmak üzere
|x – y| + |z – y| – |z – y|
ifadesinin eşiti aşağıdakilerden hangisidir?

A) -x+y     B) x-y      C) -x-z
D) -x-y      E) x-z

Doğru Cevap Çözüm için Tıklayınız

SORU 3

-2 < x < 4 olmak üzere,
|x – 6| + |x + 3| + |4 – x|
ifadesinin eşiti aşağıdakilerden hangisidir?

A) 2x-1   B) 1-x     C) 13-x
D) x+3   E) 2x+13

Doğru Cevap Çözüm için Tıklayınız

SORU 4

2 < x < 3 olduğuna göre,
||x – 2| + 1| + ||x + 2| – 5|
ifadesinin eşiti aşağıdakilerden hangisidir?

A) 2          B) x+2 C) 2x+10
D) 2x-4    E) 10

Doğru Cevap Çözüm için Tıklayınız

SORU 5

x < 0 olduğuna göre,

\displaystyle \frac{{x+||2x|-3x|}}{{|-2x|}}

ifadesinin eşiti aşağıdakilerden hangisidir?

A) 1    B) 2    C) 3     D) 4     E) 5

Doğru Cevap Çözüm için Tıklayınız

Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.

SORU 6

-1 < x < 2 olmak üzere

\displaystyle \sqrt{{{{x}^{2}}+2x+1}}+\sqrt{{{{x}^{2}}-4x+4}}

işleminin sonucu kaçtır?

A) 1    B) 2    C) 3    D) 4     E) 5

Doğru Cevap Çözüm için Tıklayınız

SORU 7

\displaystyle \sqrt{{x+3}}+|y-2|+{{(z-5)}^{2}}=0

olduğuna göre, x + y + z toplamı kaçtır?

A) 0     B) 1     C) 2     D) 3     E) 4

Doğru Cevap Çözüm için Tıklayınız

SORU 8

3.|x – 4| + 5 = 17
denklemini sağlayan x değerlerinin toplamı kaçtır ?

A) 5    B) 6    C) 7    D) 8    E) 10

Doğru Cevap Çözüm için Tıklayınız

SORU 9

|x – 3| + |3 – x| |2x – 6| = 24

denklemini sağlayan x değerlerinin toplamı kaçtır?

A) 6     B) 8      C) 9     D) 12      E) 15

Doğru Cevap Çözüm için Tıklayınız

SORU 10

|2x|+|-2x|+3|x|+|-7x|=64
denklemini sağlayan x değerlerinin çarpımı kaçtır?

A) -48   B) -64    C) -80    D) -88     E) -92

Doğru Cevap Çözüm için Tıklayınız

SORU 11

||2x+3|-8|=5
denklemini sağlayan x değerlerinin toplamı kaçtır?

A) 2   B) 3   C) 4   D) 5     E) 6

Doğru Cevap Çözüm için Tıklayınız

SORU 12

|4x + 9| = |2x + 13|
denklemini sağlayan x değerlerinin çarpımı kaçtır?

\displaystyle \begin{array}{*{20}{l}} {A)-\frac{{22}}{3}} & {B)-\frac{{25}}{6}} & {C)-\frac{{21}}{5}} & {D)-\frac{{17}}{3}} & {E)-\frac{{32}}{3}} \end{array}

 

Doğru Cevap Çözüm için Tıklayınız

SORU 13

2x+|3x-9|=21
denkleminin çözüm kümesi aşağıdakilerden hangisidir?

A) { -6,12}    B) { -6,8}     C) { -12,6}
D) { -10,6}    E) { -12,8}

Doğru Cevap Çözüm için Tıklayınız

SORU 14

3x-|x|=12
denkleminin çözüm kümesi aşağıdakilerden hangisidir?

A) { -6,3}    B) { -3,6}      C) {3,6}
D) {6}          E) { -3,-6}

Doğru Cevap Çözüm için Tıklayınız

SORU 15

|x – 2| = |x² – 4|
denkleminin çözüm kümesi aşağıdakilerden hangisidir?

A) { -1,2}      B) { -3,1,2}      C) {1,2,3}
D) { -3, -1}   E) { -3, -1,2}

Doğru Cevap Çözüm için Tıklayınız

SORU 16

||x – 4| + x – 4|= 0
denklemini sağlayan x doğal sayılarının toplamı kaçtır?

A) 5   B) 6   C) 7   D) 8   E) 10

Doğru Cevap Çözüm için Tıklayınız

SORU 17

|x – 4| + |x – 2| + |x + 3|
ifadesinin alabileceği en küçük değer kaçtır?

A) 7   B) 9    C) 12    D) 15    E) 18

Doğru Cevap Çözüm için Tıklayınız

SORU 18

|2x – 4| + 3 ≤ 9
eşitsizliğini sağlayan kaç farklı x tam sayı değeri vardır?

A) 7   B) 9    C) 12    D) 15    E) 18

Doğru Cevap Çözüm için Tıklayınız

SORU 19

|x + 2| + |2x + 4| > 15
eşitsizliğinin çözüm kümesi aşağıdakilerden hangisidir?

A) (-∞ , -7) (3,7)      B) (-3,3) (7, ∞)
C) (-∞ , -7) (7, ∞)    D) ( -∞, -7) (3,∞)
E) (- ∞, -3) (7,∞ )

Doğru Cevap Çözüm için Tıklayınız

SORU 20

2 ≤ |2x + 6| ≤ 8
eşitsizliğini sağlayan kaç farklı x tam sayı değeri vardır?

A) 7     B) 8     C) 12     D) 15       E) 18

Doğru Cevap Çözüm için Tıklayınız

SORU 21

|x + 3| + |x – 2| = 5
denklemini sağlayan x tam sayı değerlerinin toplamı kaçtır?

A) -5     B) -4     C) -3     D) -2      E) -1

Doğru Cevap Çözüm için Tıklayınız

SORU 22

|x + 3| < |x + 5|
Eşitsizliğinin çözüm aralığı aşağıdakilerden hangisidir?

A) ( -4, ∞)    B) ( -4,3]    C) ( -3,∞ )
D) [ -4,∞ )    E) ( -∞,4)

Doğru Cevap Çözüm için Tıklayınız
Eğer çözümler konusunda anlaşılmayan bir yer görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.

SORU ÇÖZÜMLERİ

ÇÖZÜM 22

\displaystyle |x+3|\text{ }<\text{ }|x+5|
\displaystyle |x+3|\text{ }-\text{ }|x+5|\text{ }<\text{ }0
Bu eşitsizlikte 2 kritik nokta var dır. Mutlak değerlerin içini 0 yapan x değerleri kritik
noktalardır.
1.aralık : \displaystyle {x<-5} için;
\displaystyle |x+3|-|x+5|\text{ }<\text{ }0
\displaystyle -x-3-(-x-5)\text{ }<\text{ }0
\displaystyle -x-3+x+5<0
\displaystyle 2\text{ }<\text{ }0\text{ }\Rightarrow Çözüm Kümesi: Ø

2.aralık : \displaystyle -5\le x\le -3 için;
\displaystyle |x+3|-|x+5|\text{ }<\text{ }0
\displaystyle -x-3-x-5\text{ }<\text{ }0
\displaystyle -2x-8\text{ }<\text{ }0
\displaystyle -2x\text{ }<\text{ }8
\displaystyle x\text{ }>\text{ }-4\text{ }\Rightarrow Çözüm Kümesi : \displaystyle (-4,-3]

3.aralık : \displaystyle {x>-3} için;
\displaystyle |x+3|-|x+5|\text{ }<\text{ }0
\displaystyle x+3-x-5\text{ }<\text{ }0
\displaystyle -2\text{ }<\text{ }0\text{ }\Rightarrow Çözüm Kümesi : \displaystyle (-3,\infty )

Buna göre çözüm kümesi: \displaystyle (-4,-3]\cup (-3,\infty ) aralıklarının birleşimidir. Kısacası \displaystyle (-4,\infty ) aralığıdır.

Doğru Cevap : A şıkkı

Soruyu Gör
Eğer çözümler konusunda anlaşılmayan bir yer görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
 

ÇÖZÜM 21

\displaystyle |x+3|+|x-2|\text{ }=5\text{ } eşitliğinde 2 kritik nokta
vardır. Mutlak değerlerin içini 0 yapan x değerler, kritik noktalardır.

1.aralık : x 3\displaystyle {x<-3} için;
\displaystyle |x+3|+|x-2|\text{ }=5
\displaystyle -x-3-x+2=5
\displaystyle -2x-1=5
\displaystyle -2x=6
\displaystyle x=-3\text{ }(x<-3\text{ }de\breve{g}il)

2.aralık : \displaystyle -3\le x\le 2 için;
\displaystyle |x+3|+|x-2|\text{ }=5
\displaystyle x+3-x+2=5
\displaystyle 5=5 çözüm bu aralıkta her zaman sağlanır.

3.aralık : \displaystyle {x>2} için;
\displaystyle |x+3|+|x-2|\text{ }=5
\displaystyle x+3+x-2=5
\displaystyle 2x+1=5
\displaystyle 2x=4
\displaystyle x=2\text{ }(\text{ }x>2\text{ }de\breve{g}il)

Buna göre çözüm kümesi: [ -3,2] aralığıdır.
Bu aralıktaki tam sayılar : \displaystyle -3,-2,-1,0,1,2
Toplamı: -3 tür.

Doğru Cevap : C şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 20

Mutlak değerli ifade, iki sayının arasında bir değer alıyorsa;
ya içerideki ifade bu sayıların arasındadır.
ya da eksi ile çarpılmış hali bu sayıların arasındadır. Buna göre;

\displaystyle 2\text{ }\le \text{ }|2x+6|\text{ }\le \text{ }8
\displaystyle 2\text{ }\le \text{ }2x+6\text{ }\le \text{ }8\text{ }veya\text{ }2\text{ }\le \text{ }-2x-6\text{ }\le \text{ }8
\displaystyle -4\text{ }\le \text{ }2x\text{ }\le \text{ }2\text{ }8\text{ }\le \text{ }-2x\text{ }\le \text{ }14
\displaystyle -2\text{ }\le \text{ }x\text{ }\le \text{ }1\text{ }-7\text{ }\le \text{ }-2x\text{ }\le \text{ }-4
\displaystyle x\Rightarrow -2,-1,0,1\text{ }x\Rightarrow -7,-6,-5,-4

Toplam 8 farklı x tam sayısı vardır.

Doğru Cevap : B şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 19

\displaystyle |x+2|\text{ }+\text{ }|2x+4|\text{ }>\text{ }15
\displaystyle |x+2|\text{ }+\text{ }2|x+2|\text{ }>\text{ }15
\displaystyle 3.|x+2|\text{ }>\text{ }15
\displaystyle |x+2|\text{ }>\text{ }5

Mutlak değerli ifade bir sayıdan büyük ise;
içerideki ifade, bu sayıdan büyük veya eksi ile çarpımından daha küçüktür. Buna göre;

\displaystyle |x+2|\text{ }>\text{ }5
\displaystyle x+2\text{ }>\text{ }5\text{ }veya\text{ }x+2\text{ }<\text{ }-5
\displaystyle x>3\text{ }x<-7
Çözüm Kümesi: \displaystyle (-\infty ,-7)\cup (3,\infty )

Doğru Cevap : D şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 18

\displaystyle |2x-4|+3\le 9
\displaystyle |2x-4|\le 6\text{ }

Mutlak değerli ifade bir sayıdan küçük ise;
içerideki ifade bu sayı ile onun eksi ile çarpımı arasındadır. Buna göre;

\displaystyle -6\le 2x-4\le 6
\displaystyle -6+4\le 2x\le 6+4 (Her tarafa 4 ekleyelim.)
\displaystyle -2\le 2x\le 10 (Her tarafı 2 ye bölelim.)
\displaystyle -1\le x\le 5

x’in alabileceği değerler;
-1,0,1,2,3,4,5 olup 7 tanedir.

Doğru Cevap : A şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 17

Her bir mutlak değer içini 0 yapan x değerini sırayla deneyelim.

\displaystyle |\underbrace{{x-4}}_{{0\text{ }icin\text{ }x=4}}|+|x-2|+|x+3|
\displaystyle |0|+|4-2|+|4+3|=0+2+7=9

\displaystyle |x-4|+|\underbrace{{x-2}}_{{0\text{ icin x=2}}}|+|x+3|
\displaystyle |2-4|+|0|+|2+3|=2+0+5=7

\displaystyle |x-4|+|x-2|+|\underbrace{{x+3}}_{{0\text{ icin x=}-3}}|
\displaystyle |-3-4|+|-3-2|+|0|=7+5=12

En küçük değeri 7 buluruz.

Doğru Cevap : A şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 16

x’in 4’ten büyük olup olmamasına göre 2 durum vardır.

\displaystyle \underline{{1.durum:\text{ }x\ge 4}}
\displaystyle ||x-4|+x-4|=0\text{ }\Rightarrow \text{ }|x-4+x-4|=0
\displaystyle |2x-8|=0\text{ }\Rightarrow \text{ }2x-8=0
\displaystyle 2x=8\text{ }\Rightarrow \text{ }x=4

\displaystyle \underline{{2.durum:\text{ }x<4}}
\displaystyle ||x-4|+x-4|=0\text{ }
\displaystyle |4-x+x-4|=0
\displaystyle |0|=0\text{ }\Rightarrow \text{ }x<4 için her zaman sağlanır.

Buna göre denklemi sağlayan doğal sayılar; 0,1,2,3,4
Toplamı: \displaystyle 0+1+2+3+4=10 buluruz.

Doğru Cevap : E şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 15

Denklemi düzenleyip; iki kare farkından yararlanalım.

\displaystyle |x-2|\text{ }=\text{ }|{{x}^{2}}-4|
\displaystyle |x-2|\text{ }-\text{ }|{{x}^{2}}-4|\text{ }=\text{ }0
\displaystyle |x-2|\text{ }-\text{ }|x-2|.|x+2|\text{ }=\text{ }0
\displaystyle |x-2|.\{1-|x+2|\}=0
\displaystyle x-2=0\text{ }veya\text{ }1-|x+2|=0
\displaystyle x=2\text{ }|x+2|=1
\displaystyle \text{ }x+2=1\text{ }veya\text{ }x+2=-1
\displaystyle \text{ }x=-1\text{ }veya\text{ }x=-3

Çözüm Kümesi: { -3, -1,2}

Doğru Cevap : E şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 14

Mutlak değerin içindeki değerin pozitif veya negatif olmasına göre denklem değişmektedir.

\displaystyle \underline{{1.durum:\text{ }x\ge 0\text{ }ise;}}
\displaystyle 3x-|\underbrace{x}_{+}|=12
\displaystyle 3x-x=12
\displaystyle 2x=12
\displaystyle x=6 bulunur. (x \displaystyle \ge 0 durumuna da uyuyor)

\displaystyle \underline{{2.durum:\text{ }x<0\text{ }ise;}}\text{ }
\displaystyle 3x-|\underbrace{x}_{-}|=12
\displaystyle 3x-(-x)=12
\displaystyle 4x=12
\displaystyle x=3 bulunur. (\displaystyle x<0 durumuna uymuyor, alamayız.)
Çözüm Kümesi : {6} dır.

Doğru Cevap : D şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 13

Mutlak değerin içindeki değerin pozitif veya negatif olmasına göre denklem değişmektedir.

\displaystyle \underline{{1.durum:\text{ }x\ge 3\text{ }ise;}}
\displaystyle 2x+|\underbrace{{3x-9}}_{+}|=21
\displaystyle 2x+3x-9=21
\displaystyle 5x=30
\displaystyle x=6 bulunur. (\displaystyle x\ge 3 durumuna da uyuyor)

\displaystyle \underline{{2.durum:\text{ }x<3\text{ }ise;}}\text{ }
\displaystyle 2x+|\underbrace{{3x-9}}_{-}|=21
\displaystyle 2x-3x+9=21
\displaystyle -x=12
\displaystyle x=-12 bulunur. (\displaystyle x<3 durumuna da uyuyor)

Çözüm Kümesi : \displaystyle \{-12,6\} dır.

Doğru Cevap : C şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 12

İki mutlak değerli ifade birbirine eşit ise;
ya içerideki ifadeler birbirine eşittir.
ya da ifadelerden birinin eksi ile çarpımına eşittir.
\displaystyle |4x+9|=|2x+13|
\displaystyle 4x+9=2x+13\text{ }veya\text{ }4x+9=-2x-13
\displaystyle 4x-2x=13-9\text{ }4x+2x=-13-9
\displaystyle \text{ }2x=4\text{ }6x=-22
\displaystyle \text{ }x=2\text{ }x=-\frac{{11}}{3}
\displaystyle De\breve{g}erlerin\text{ carp }\!\!\imath\!\!\text{ m }\!\!\imath\!\!\text{ : 2}\text{.(}-\frac{{11}}{3}\text{)=}-\frac{{22}}{3}\text{ buluruz}

Doğru Cevap : A şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 11

Denklemi adım adım çözmeye çalışalım.
\displaystyle ||2x+3|-8|=5
\displaystyle |2x+3|-8=5\text{ }veya\text{ }|2x+3|-8=-5
\displaystyle |\underbrace{{2x+3}}_{{13\text{ }veya\text{ }-13}}|=13\text{ }|\underbrace{{2x+3}}_{{3\text{ }veya\text{ }-3}}|=3
\displaystyle 2x+3=13\text{ }2x+3=3
\displaystyle \text{ }2x=10\text{ }2x=0
\displaystyle \text{ }x=5\text{ }veya\text{ }x=0\text{ }veya
\displaystyle 2x+3=-13\text{ }2x+3=-3
\displaystyle \text{ }2x=-16\text{ }2x=-6
\displaystyle \text{ }x=-8\text{ }x=-3\text{ }

Bulduğumuz 4 değerin toplamı:
\displaystyle 5+(-8)+0+(-3)=-6 buluruz.

Doğru Cevap : E şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 10

\displaystyle |2x|+|-2x|-3|x|+|-7x|=64
\displaystyle \text{ }2.|x|+2.|x|-3.|x|+7.|x|=64
\displaystyle \text{ }|x|.(2+2-3+7)=64
\displaystyle \text{ }|x|.8=64
\displaystyle \text{ }|x|=8

Değerler çarpımı: \displaystyle 8.(-8)=-64 buluruz.

Doğru Cevap : B şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 9

Mutlak değerli ifadeleri birbirine benzeyecek şekilde yazıp, onları ortak paranteze almaya çalışalım.
\displaystyle \text{ }|x-3|+|3-x|+|2x-6|=24
\displaystyle |x-3|+|(-1).(x-3)|+|2.(x-3)|=24
\displaystyle |x-3|+\underbrace{{|-1|}}_{1}.|x-3|+\underbrace{{|2|}}_{2}.|x-3|=24
\displaystyle |x-3|+|x-3|+2.|x-3|=24
\displaystyle \text{ }|x-3|.(1+1+2)=24
\displaystyle \text{ }|x-3|.4=24
\displaystyle \text{ }|x-3|=6
\displaystyle \text{ }x-3=6\text{ }veya\text{ }x-3=-6
\displaystyle \text{ }x=9\text{ }x=-3\text{ }

Değerler toplamı:\displaystyle 9+(-3)=6 buluruz.

Doğru Cevap : A şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 8

Mutlak değerli ifadeyi yalnız bırakacak şekilde denklemi çözmeye başlayalım.
\displaystyle 3.|x-4|+5=17
\displaystyle 3.|x-4|=12
\displaystyle |\underbrace{{x-4}}_{{4\text{ }veya\text{ }-4}}|=4 Bu durumda iki seçenek vardır.
\displaystyle x-4=4\text{ }x-4=-4
\displaystyle \text{ }x=8\text{ }x=0

Toplam: \displaystyle 8+0=8 buluruz.

Doğru Cevap : D şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 7

Derecesi çift olan köklü ifadeler, Mutlak Değerli ifadeler ile Üssü çift olan ifadeler negatif olamaz.
Soruda verilen eşitlik, 0 ‘ a eşit olduğu için her bir terim 0’a eşit olmak zorundadır.

\displaystyle \underbrace{{\sqrt{{x+3}}}}_{0}+|\underbrace{{y-2}}_{0}|+{{(\underbrace{{z-5}}_{0})}^{2}}=0
\displaystyle x+3=0\text{ }\Rightarrow \text{ }x=-3
\displaystyle y-2=0\text{ }\Rightarrow \text{ }y=2
\displaystyle z-5=0\text{ }\Rightarrow \text{ }z=5 Buna göre;
\displaystyle z-5=0\text{ }\Rightarrow \text{ }z=5 buluruz.

Doğru Cevap : E şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 6

Köklü ifadeler içerisinde yer alan ifadelerin tam kare ifadeler olduğunu görüyoruz. Buna göre;

\displaystyle \sqrt{{{{x}^{2}}+2x+1}}+\sqrt{{{{x}^{2}}-4x+4}}
\displaystyle =\sqrt{{{{{(x+1)}}^{2}}}}+\sqrt{{{{{(x-2)}}^{2}}}}

Tam kare ifadeler, köklü ifadelerin dışına mutlak değer içerisinde çıkar.
Buna göre;

\displaystyle \sqrt{{{{{(x+1)}}^{2}}}}+\sqrt{{{{{(x-2)}}^{2}}}}=|x+1|+|x-2|
\displaystyle -1<x<2 olmak üzere
\displaystyle |\underbrace{{x+1}}_{+}|+|\underbrace{{x-2}}_{-}|=x+1-(x-2)
\displaystyle \text{ }=x+1-x+2

\displaystyle \text{ }=3\text{ }buluruz.

Doğru Cevap : C şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 5

Mutlak değerli ifadeleri dışarıya çıkarmaya çalışarak çözüme gidelim.
x < 0 olduğuna göre,

\displaystyle \frac{{x+||\overbrace{{2x}}^{-}|-3x|}}{{|-2x|}}=\frac{{x+|-2x-3x|}}{{|-2x|}}
\displaystyle \frac{{x+|\overbrace{{-5x}}^{+}|}}{{|\underbrace{{-2x}}_{+}|}}=\frac{{x-5x}}{{-2x}}=\frac{{-4x}}{{-2x}}=2\text{ buluruz}\text{.}

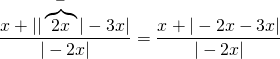
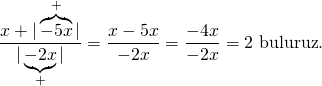
Doğru Cevap : B şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 4

İlk önce, en içerideki mutlak değerleri dışarı çıkarmaya çalışalım.

\displaystyle 2<x<3 olduğuna göre,
\displaystyle ||\underbrace{{x-2}}_{\begin{smallmatrix} pozitif \\ x\text{ }>\text{ }2 \end{smallmatrix}}|+1|+||\underbrace{{x+2}}_{\begin{smallmatrix} pozitif \\ x\text{ }>\text{ }2 \end{smallmatrix}}|-5|

\displaystyle |x-2+1|+|x+2-5|

\displaystyle =|\underbrace{{x-1}}_{\begin{smallmatrix} pozitif \\ x\text{ }>\text{ }2 \end{smallmatrix}}|+|\underbrace{{x-3}}_{\begin{smallmatrix} negatif \\ \text{ }x\text{ }<\text{ }3 \end{smallmatrix}}|

\displaystyle =x-1+3-x

\displaystyle =2\text{ }bulunur.

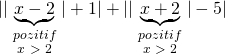
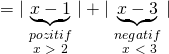
Doğru Cevap : A şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 3

Mutlak değerlerin içindeki ifadelere bakalım. Negatif olanları ile çarparak mutlak değerden çıkaralım.

\displaystyle -2<x<4 olmak üzere,
\displaystyle \text{ }\!\!|\!\!\text{ }\underbrace{{\text{x}-6}}_{{negatif}}|+|\underbrace{{x+3}}_{{pozitif}}|+|\underbrace{{4-x}}_{{pozitif}}|
\displaystyle =-(x-6)\text{ }+\text{ }(x+3)+(4-x)
\displaystyle =-x+6+x+3+4-x
\displaystyle =13-x bulunur.

Doğru Cevap : C şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 2

Mutlak değer içerisindeki değer, negatif ise ile çarparak dışarı çıkılır. Diğer durumlarda aynen dışarı çıkartılır.
\displaystyle x<0<y<z\text{ }
\displaystyle \text{ }|\underbrace{{x-y}}_{{negatif}}|+|\underbrace{{z-y}}_{{pozitif}}|-|\underbrace{{z+y}}_{{pozitif}}|
\displaystyle =-(x-y)+(z-y)-(z+y)
\displaystyle =-x+y+z-y-z-y

Doğru Cevap : D şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 1

İlk önce mutlak değerlerin içindeki işlemleri yapalım.

\displaystyle |6-2|+|2-5|-|1+4|\text{ }=\text{ }|4|+|-3|-|5|

Mutlak değerin içindeki değer, dışarıya daima pozitif olarak çıkar. Buna göre;

\displaystyle \underbrace{{|4|}}_{4}+\underbrace{{|-3|}}_{3}-\underbrace{{|5|}}_{5}=4+3-5=2 bulunur.

Doğru Cevap : B şıkkı

Soruyu Gör Sonraki Soru
Eğer çözümler konusunda anlaşılmayan bir yer görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
 

“Mutlak Değer (Latex Formatı)” üzerine 3 yorum

Yorum yapın