11.SORU
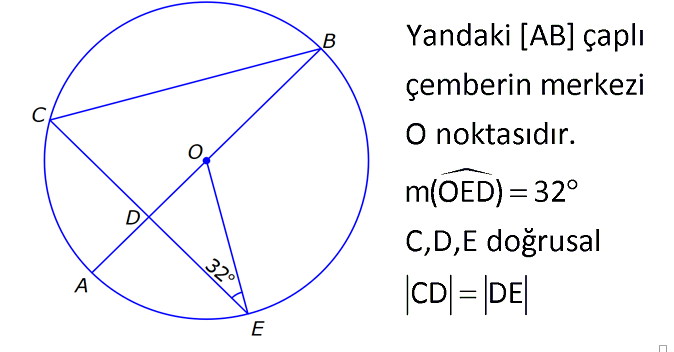
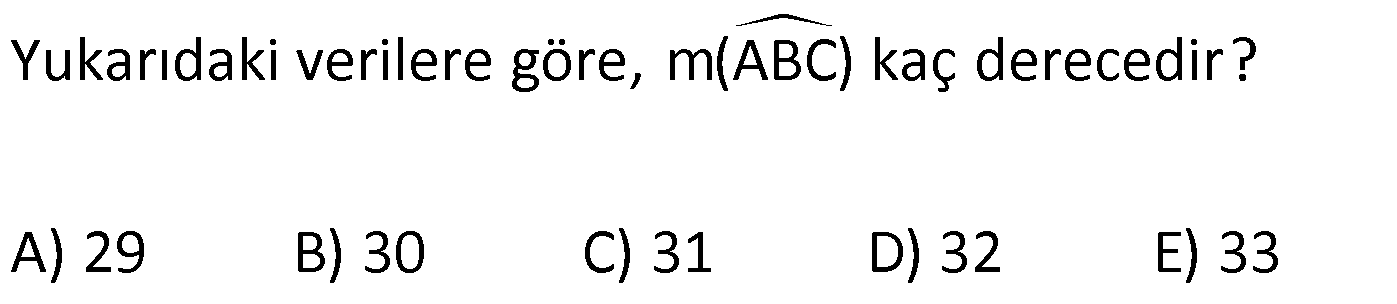
 | | | | |
Çözüm için Tıklayınız.
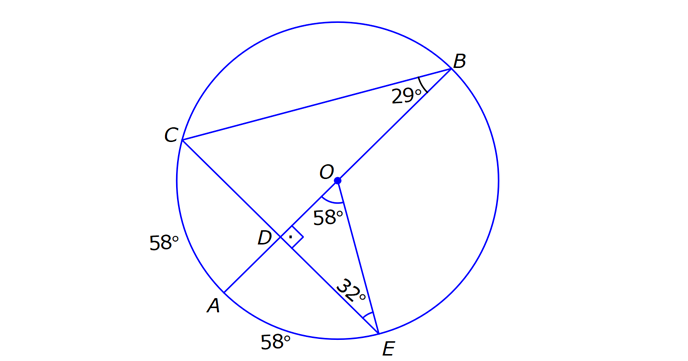

12.SORU
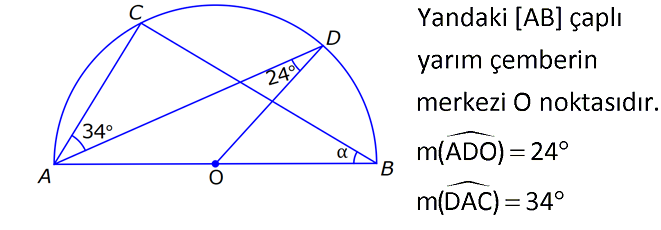
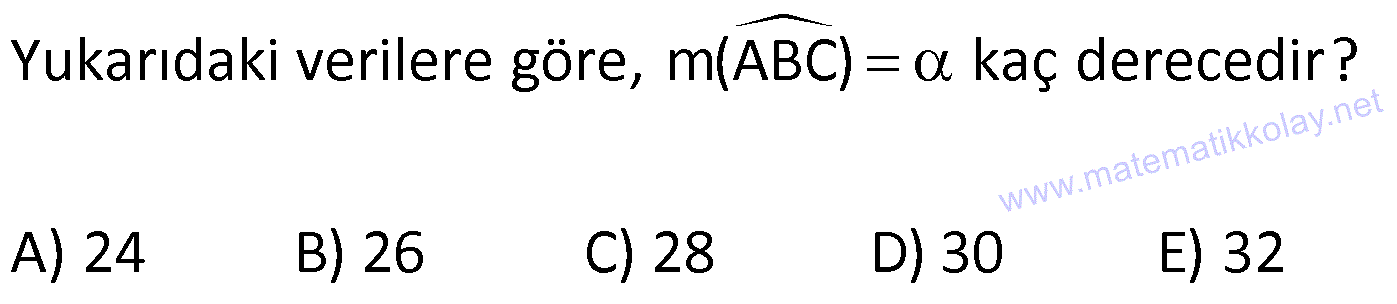
| | | | | |
Çözüm için Tıklayınız.
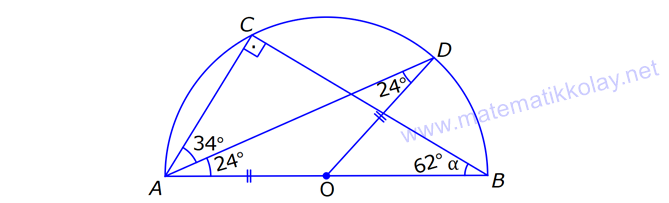

13.SORU
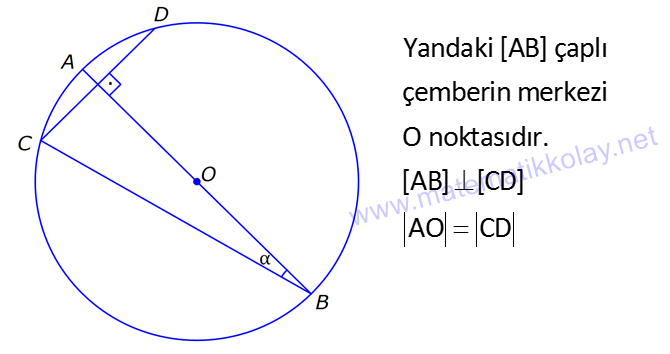
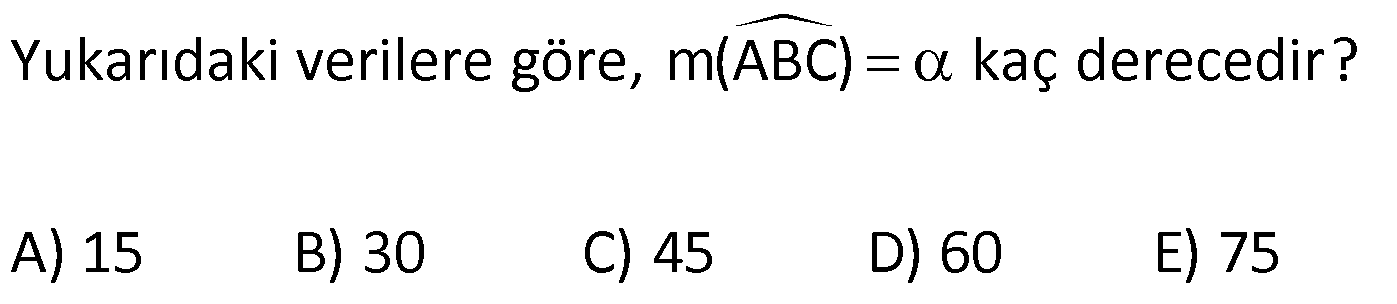
 | | | | |
Çözüm için Tıklayınız.

14.SORU
| | | | | |
Çözüm için Tıklayınız.

Sayfalar: 1 2
11.SORU

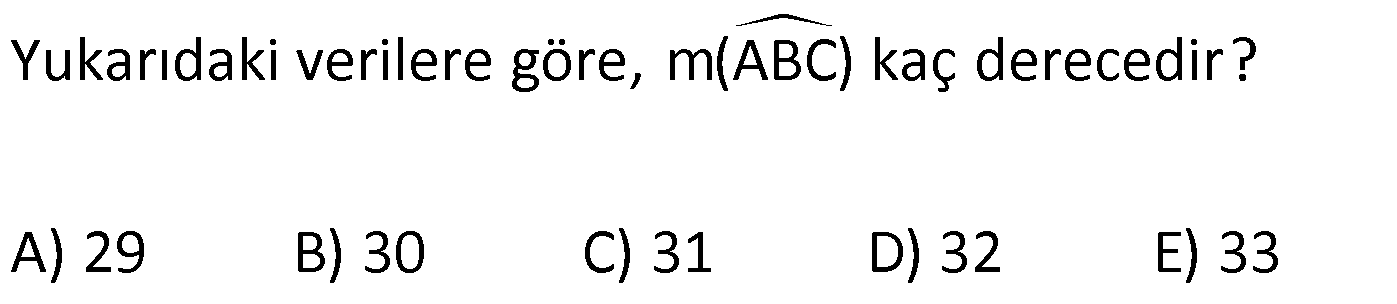
 | | | | |
Çözüm için Tıklayınız.


12.SORU

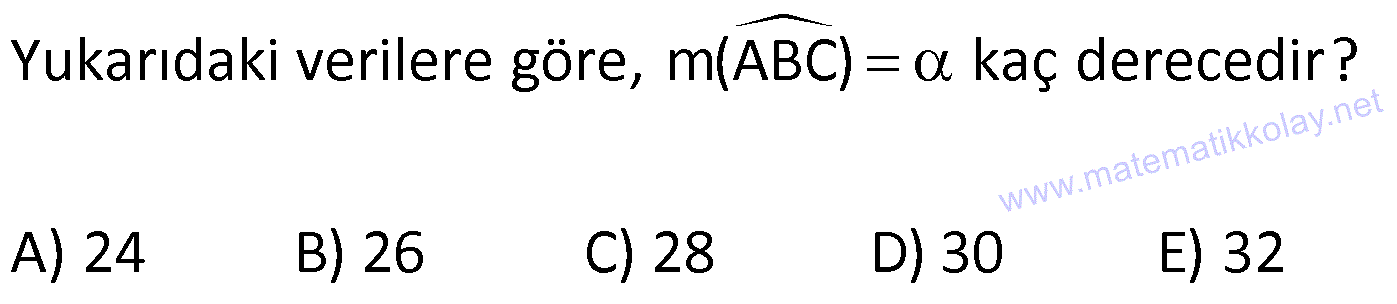
| | | | | |
Çözüm için Tıklayınız.


13.SORU

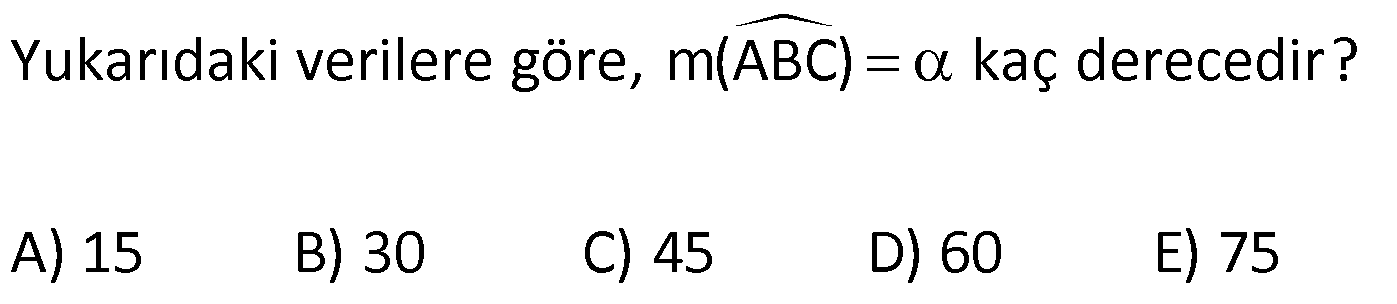
 | | | | |
Çözüm için Tıklayınız.


14.SORU

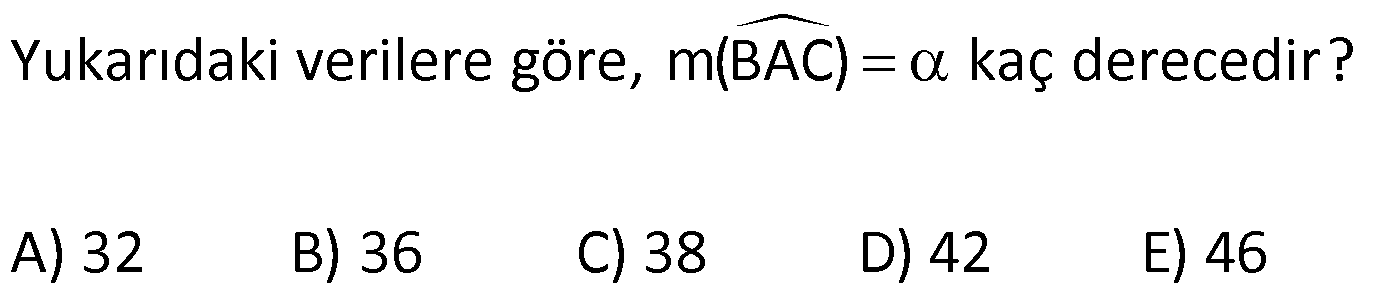
| | | | | |
Çözüm için Tıklayınız.


