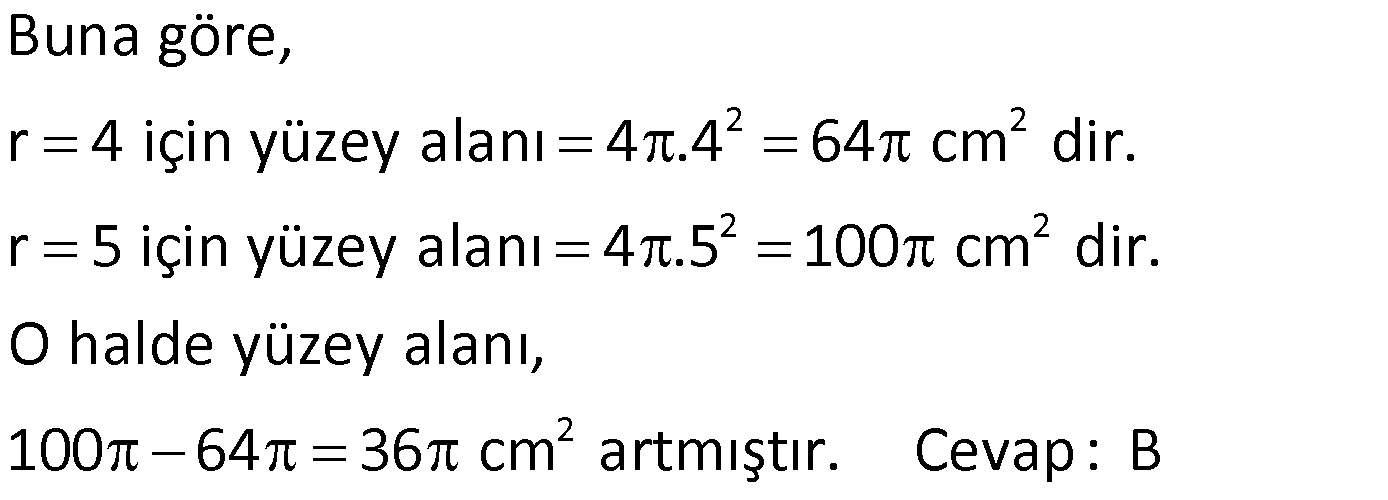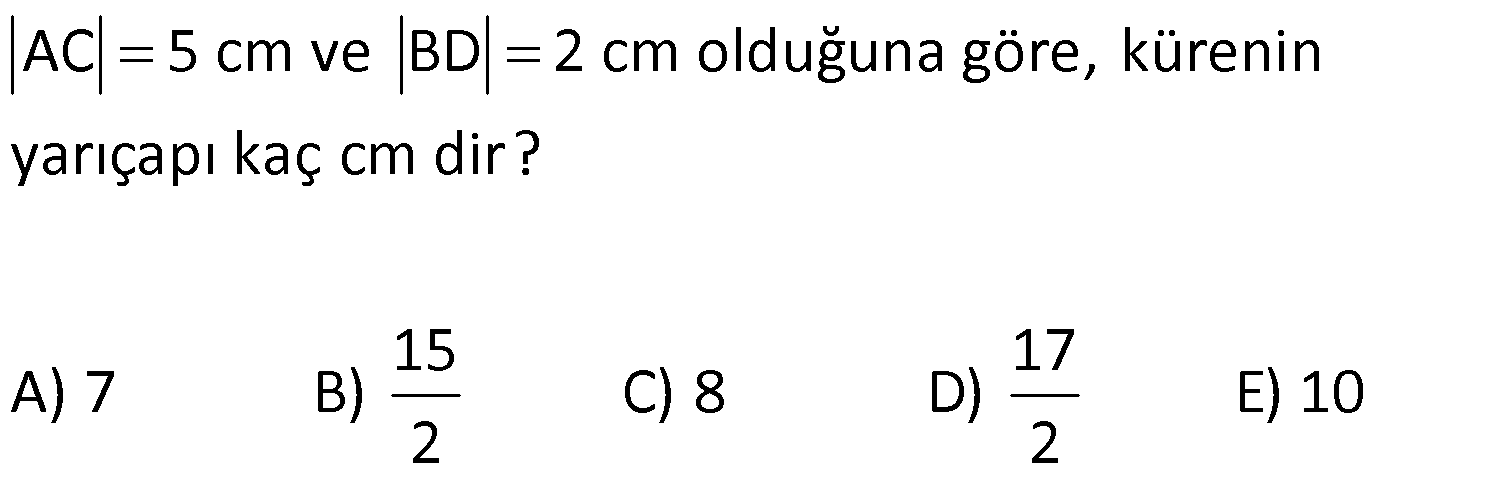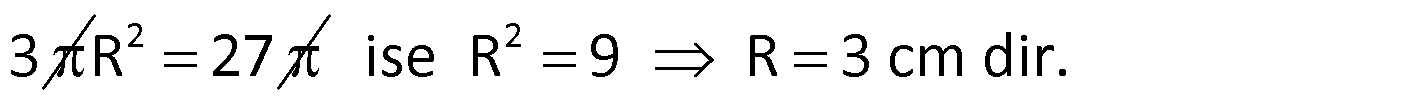Bu bölümde Küre ile ilgili 16 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
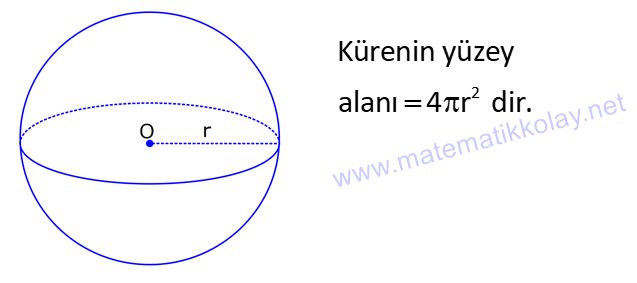
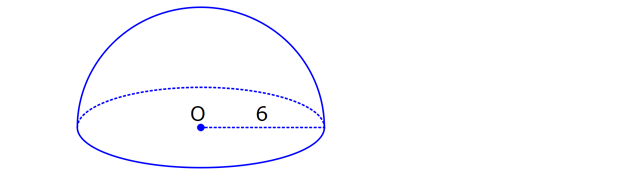
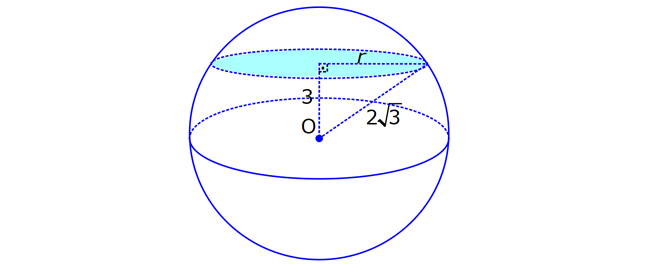
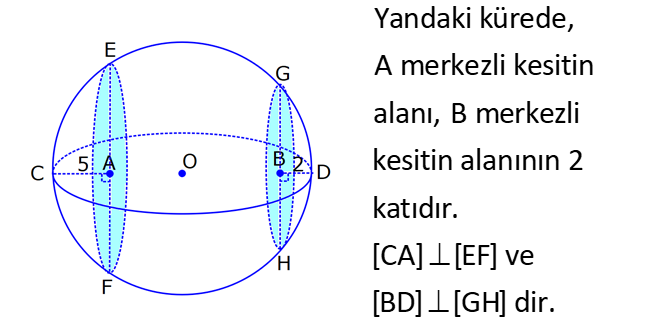
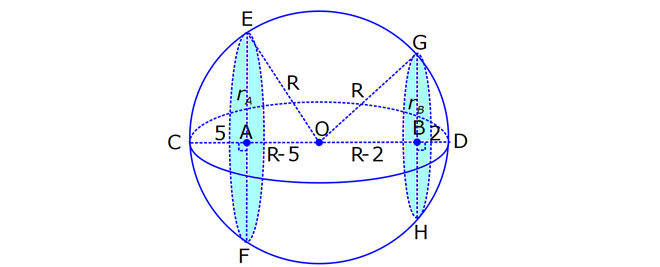
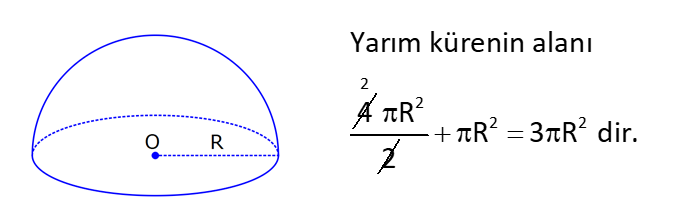
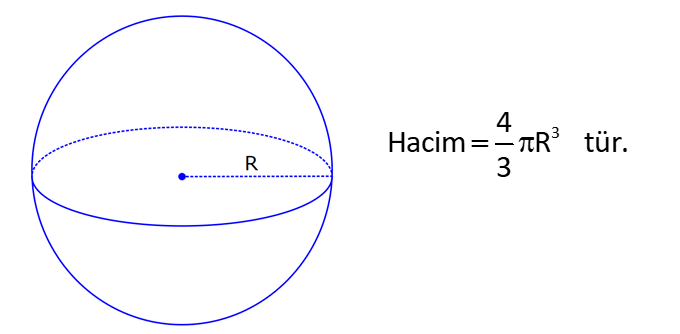
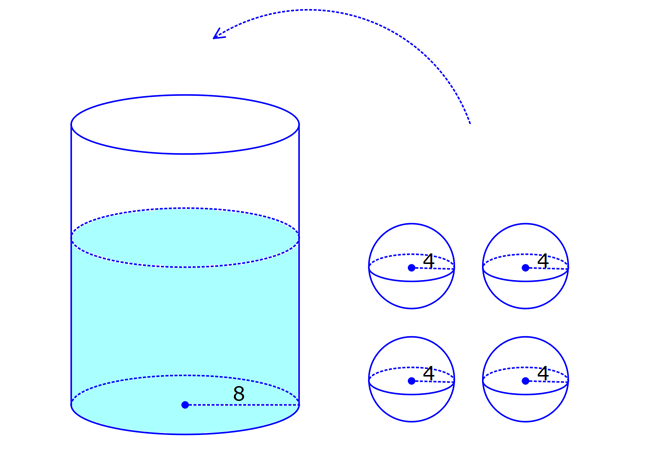
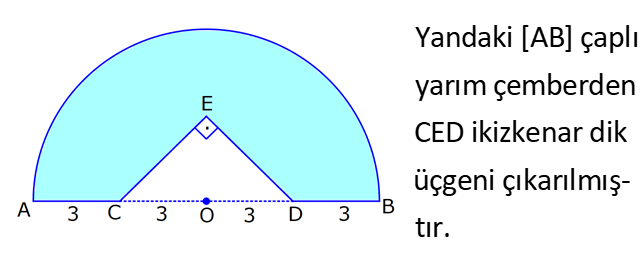
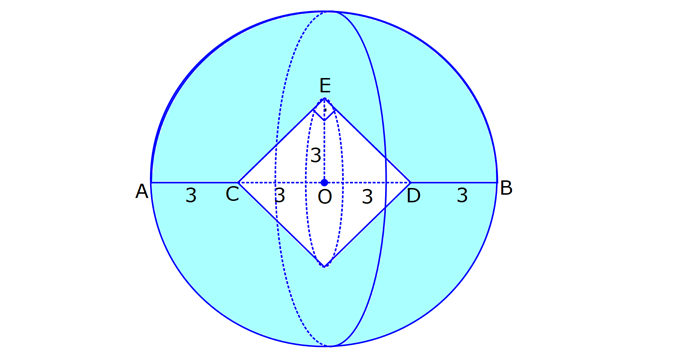
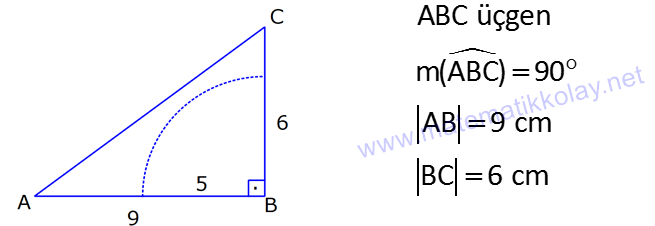
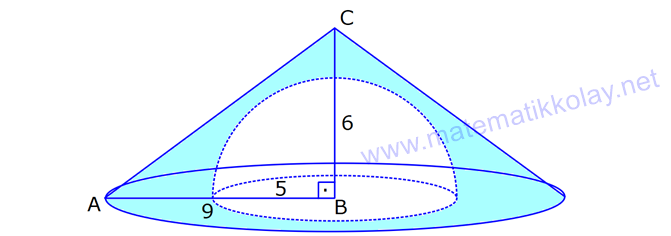
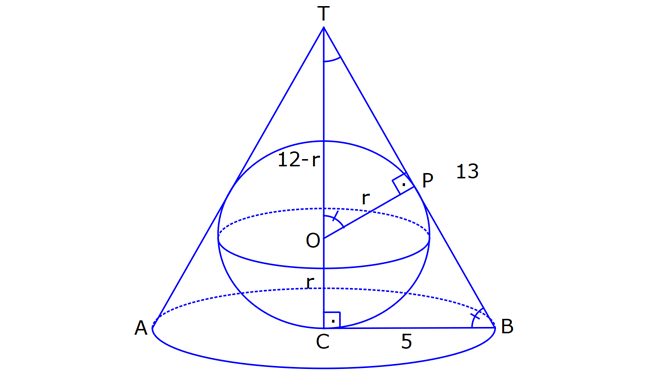
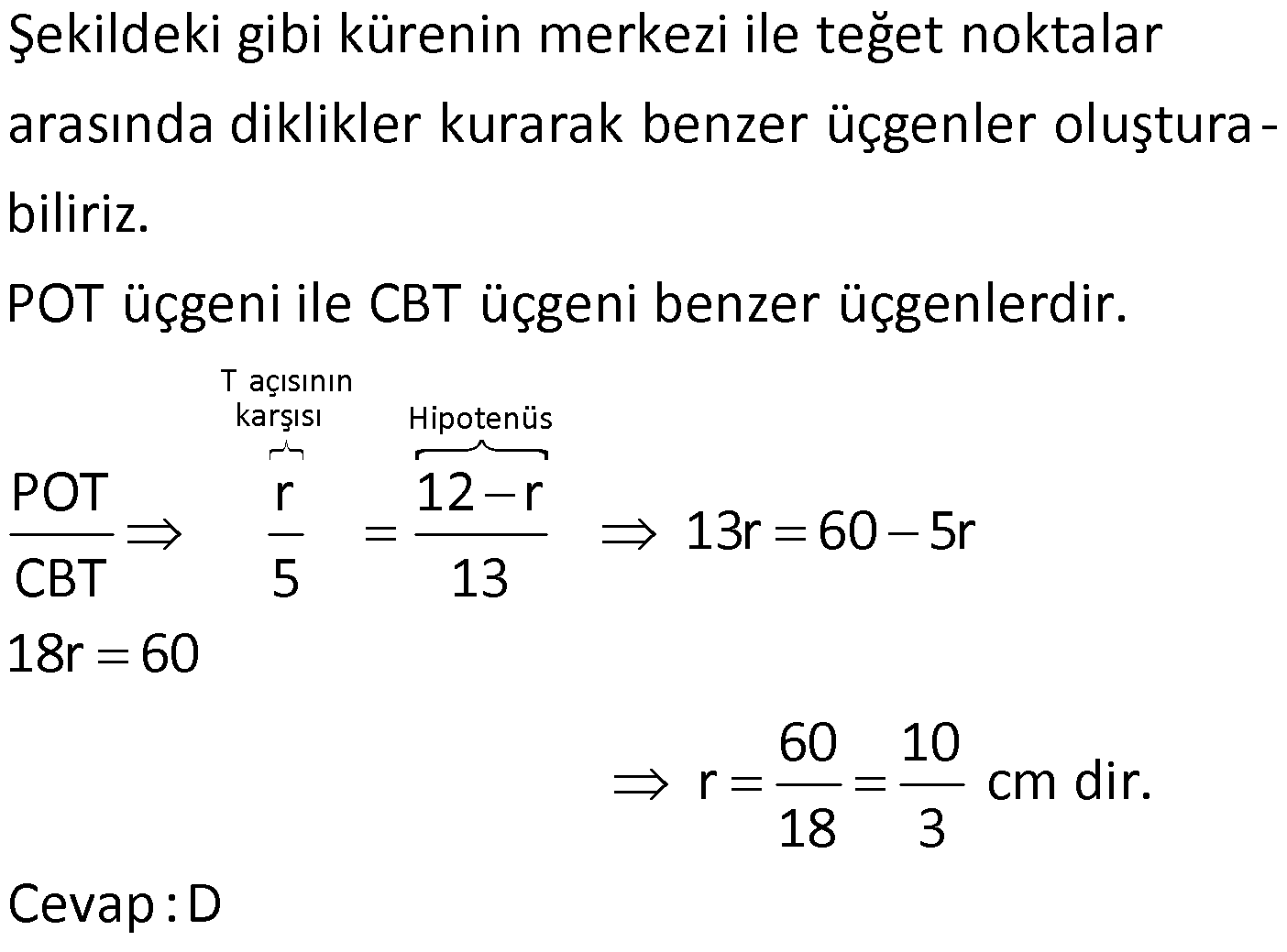
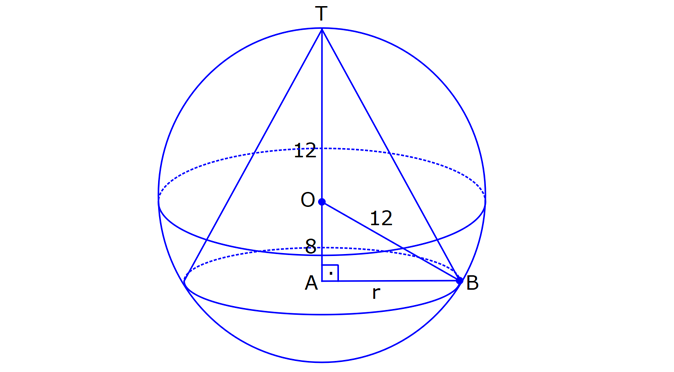
KÜRE www.matematikkolay.net 1) 2 Yarıçapı 4 cm olan kürenin yarıçapı 1 cm arttırılırsa yüzey alanı kaç cm artar? A) 10 B) 36 C) 45 D) 50 E) 61 ÇÖZÜM: 2 Kürenin yüzey alanı 4 r dir. 2 2 2 2 2 Buna göre, r 4 için yüzey alanı 4 .4 64 cm dir. r 5 için yüzey alanı 4 .5 100 cm dir. O halde yüzey alanı, 100 64 36 cm artmıştır. Cevap: B 2) 2 Yarıçapı 6 br olan bir yarım kürenin yüzey alanı kaç br dir? A) 36 B) 72 C) 108 D) 144 E) 180 ÇÖZÜM: 4 Tam kürenin alanının yarısı 2 2 .6 2 2 2 2 2 72 br dir. Tabanın alanı .6 36 br dir. O halde yüzey alanı, 72 36 108 br dir. Cevap : C 3) 2 2 Yüzey alanı 48 cm olan bir küre, merkezinden 3 cm uzaklıkta bir düzlemle kesiliyor. Oluşan arakesitin yüzey alanı kaç cm dir? 3 5 A) B) 2 C) D) 3 E) 4 2 2 ÇÖZÜM: 2 Yüzey alanı 48 cm ise, 4 2 R 48 2 R 12 R 2 3 cm dir. Merkezden 3 cm uzaklıkta bir düzlemle kesildiğinde arakesit bir daire olacaktır. 2 2 2 2 2 2 2 2 Oluşan dairenin yarıçapı r olsun. Şekildeki gibi pisagor yaparak, r yi bulabiliriz. r 3 2 3 r 9 12 r 3 r 3 cm dir. O halde dairenin alanı, r 3 3 cm dir. Cevap : D 4) Yandaki kürede, A merkezli kesitin alanı, B merkezli kesitin alanının 2 katıdır. [CA] [EF] ve [BD] [GH] dir. AC 5 cm ve BD 2 cm olduğuna göre, kürenin yarıçapı kaç cm dir? 15 17 A) 7 B) C) 8 D) E) 10 2 2 www.matematikkolay.net ÇÖZÜM: 2 2 2 A 2 2 2 A 2 2 2 A AOE üçgeninde pisagor yaparsak, r R (R 5) dir. r R (R 10R 25) r R R 2 A 2 2 2 B 2 2 2 B 2 2 2 B 10R 25 r 10R 25 tir. OBG üçgeninde pisagor yaparsak, r R (R 2) dir. r R (R 4R 4) r R R 2 B 2 A 2 B 4R 4 r 4R 4 tür. r 2 verildiğine göre, r 10R 25 2 dir. 4R 4 10R 25 8R 8 2R 25 8 2R 17 17 R cm dir. Cevap : D 2 5) 2 3 Yüzey alanı 27 cm olan bir yarım kürenin hacmi kaç cm tür? A) 18 B) 25 C) 30 D) 36 E) 45 ÇÖZÜM: Yarım kürenin alanı 4 2 2 R 2 2 2 R 3 R dir. 3 2 R 27 2 ise R 9 R 3 cm dir. 4 3 Hacim R tür. 3 3 3 Buna göre, yarım kürenin hacmi 4 3 3 36 18 cm tür. Cevap: A 2 2 6) 3 Yukarıda taban yarıçapı 8 cm olan silindirin i su 5 ile doludur. Yarıçapı 4 cm olan 4 tane demir küre içine atıldığında suyun seviyesi en üst noktaya geliyor ve su taşmıyor. Buna göre, silindirin yüksek – liği kaç cm dir? 32 40 44 A) B) 12 C) D) 15 E) 3 3 3 www.matematikkolay.net ÇÖZÜM: 4 3 3 4 5 3 2 3 4 4 Bir kürenin hacmi .4 cm tür. 3 3 4 4 4 kürenin toplam hacmi 4 cm tür. 3 3 Silindirin yüksekliği h olsun. 2h 2h Boş kısmın hacmi .8 .64 cm tür. 5 5 Bu hacim, kürelerin toplam hacmine eşit olma lıdır. 5 2h 4 .64 5 3 3 4 5 2h 4 5 2 4 3 2 2 h.3 5. 4 8 40 h cm dir. Cevap : C 3 7) Yandaki [AB] çaplı yarım çemberden CED ikizkenar dik üçgeni çıkarılmış- tır. 3 AC CO OD DB 3 cm dir. Yukarıdaki şekil [AB] kenarı etrafında 360 döndürü- lürse boyalı alanın taradığı hacim kaç cm olur? A) 210 B) 242 C) 256 D) 270 E) 288 ÇÖZÜM: 3 Üçgen çıkarılmasaydı 6 cm yarıçaplı tam küre oluşacaktı. 4 4 Bunun da hacmi 6 3 3 216 72 3 3 3 288 cm tür. Şekildeki üçgen boşluk tan dolayı yarıçapı ve yüksek – liği 3 cm olan iki tane koni boşluğu oluşur. 1 Bunların hacmi 2 3 18 cm tür. 3 O halde, boyalı bölgenin oluşturduğu hacim 288 3 18 270 cm tür. Cevap : D 8) ABC üçgen m(ABC) 90 AB 9 cm BC 6 cm 3 Yukarıdaki üçgen levhadan yarıçapı 5 cm olan B merkezli çeyrek çember çıkarılmıştır. Bu levha [BC] kenarı etrafında 360 döndürülürse, taradığı hacim kaç cm olur? 212 236 242 254 266 A) B) C) D) E) 3 3 3 3 3 ÇÖZÜM: 3 2 3 Koni Yarım Küre Koniden yarım küre çıkarılmış gibi bir görüntü oluşur. Buna göre, 4 .5 .9 .6 486 250 236 3 cm tür. 3 2 3 3 3 Cevap : B www.matematikkolay.net 9) Taban yarıçapı 5 cm ve yüksekliği 12 cm olan bir dik koninin içinde yüzeylere teğet olacak şekilde bir küre yerleştiriliyor. Buna göre, kürenin yarıçapı kaç cm dir? 5 7 8 10 A) B) C) D) E) 4 2 2 3 3 ÇÖZÜM: T açısının karşısı Hipotenüs Şekildeki gibi kürenin merkezi ile teğet noktalar arasında diklikler kurarak benzer üçgenler oluşturabiliriz. POT üçgeni ile CBT üçgeni benzer üçgenlerdir. POT r 12 r CBT 5 13 13r 60 5r 18r 60 60 10 r cm dir. 18 3 Cevap:D 10) 3 Yarıçapı 12 cm olan kürenin içine 20 cm yüksekliğinde en büyük hacimli bir dik koni yerleştiriliyor. Buna göre, koninin hacmi kaç cm tür? 800 1000 1100 1300 1600 A) B) C) D) E) 3 3 3 3 3 ÇÖZÜM: Kürenin merkezi O, koninin taban merkezi A noktası olsun. B noktası da koninin tabanının, küreye temas ettiği noktalardan biri olsun. AT 20 cm (yükseklik) olduğundan, OA 8 cm dir. OAB dik üçgeninden, koni 2 2 2 2 2 2 3 nin taban yarıçapını bulabiliriz. r 12 8 r 144 64 r 80 dir. O halde, koninin hacmi .r .h .80.20 1600 cm tür. Cevap : E 3 3 3
