Bu bölümde Kenarlarına Göre Özel Üçgenler ile ilgili 6 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
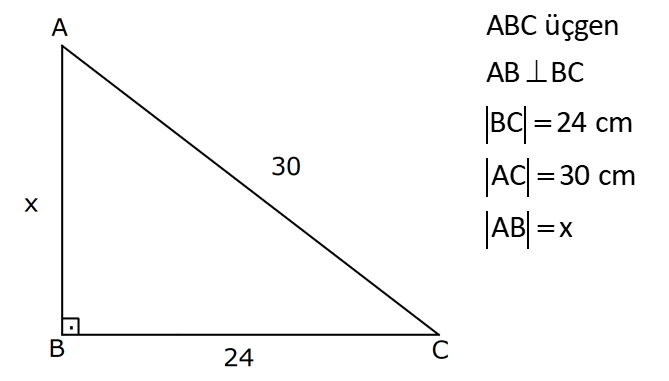
1.SORU
 |  |  |  |  |
Çözüm için Tıklayınız.
2.SORU
| | | | | |
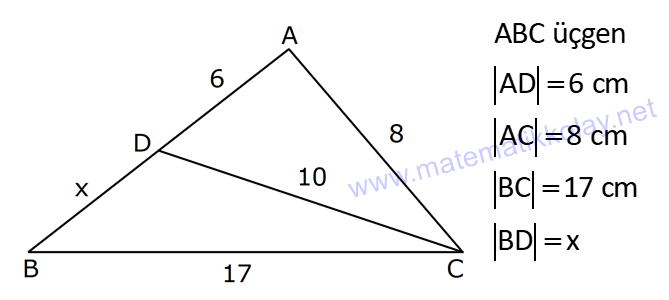
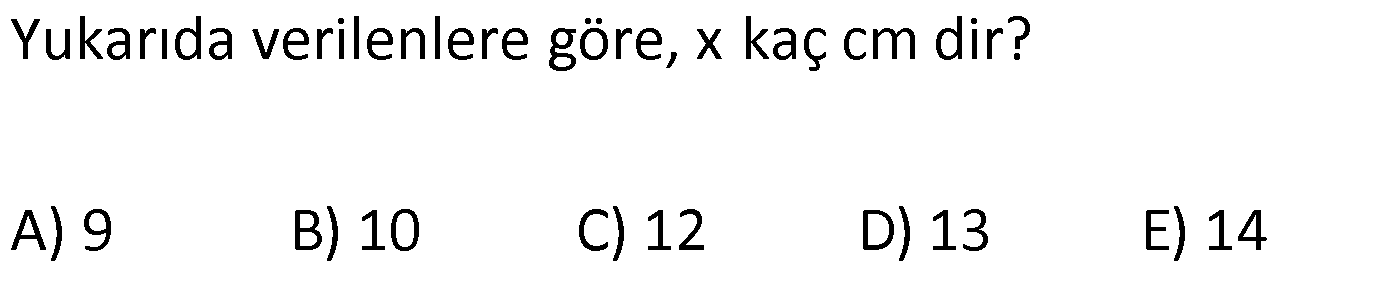
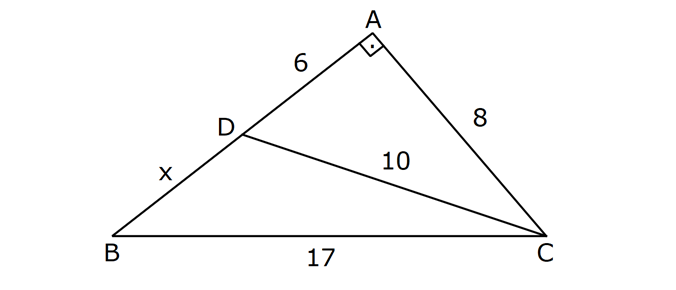
Çözüm için Tıklayınız.
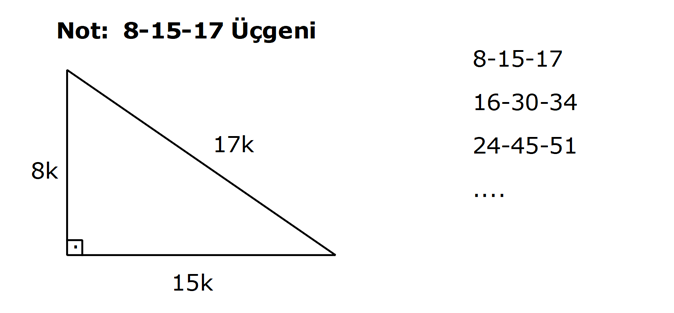
3.SORU
| | | | | |
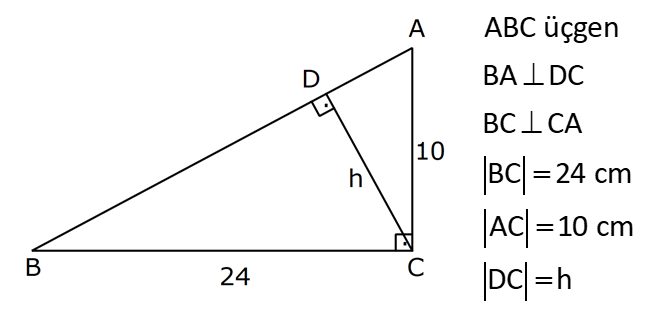
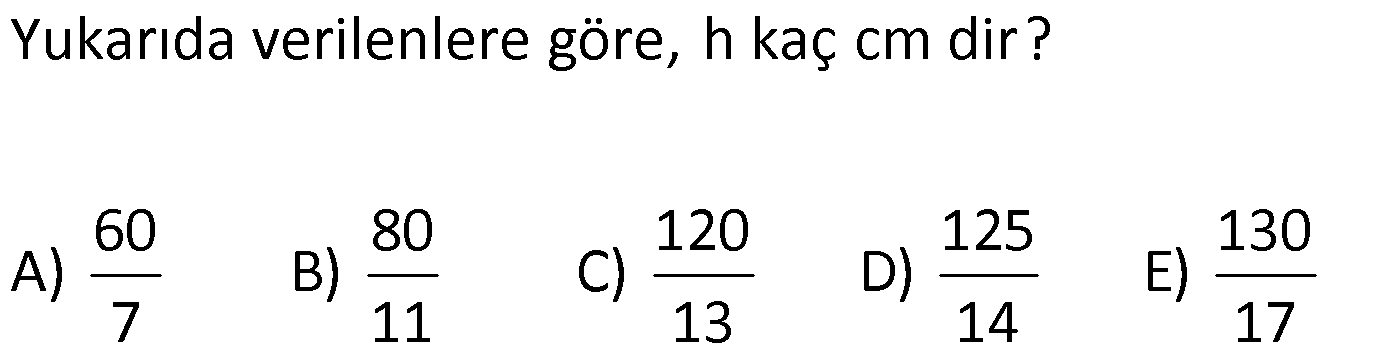
Çözüm için Tıklayınız.
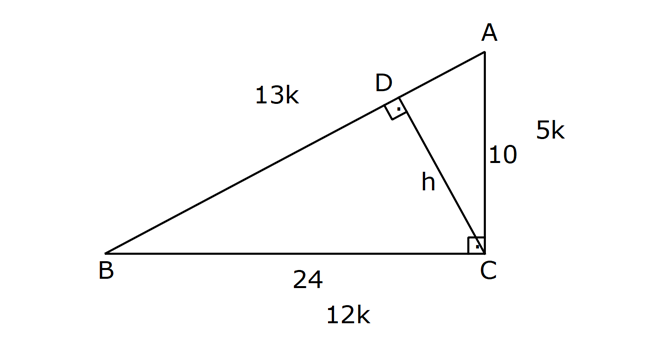
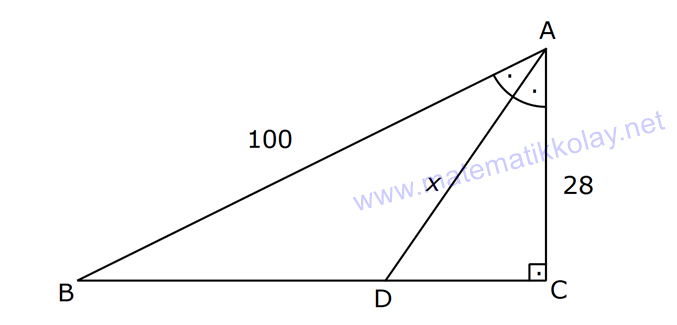
4.SORU
| | | | | |
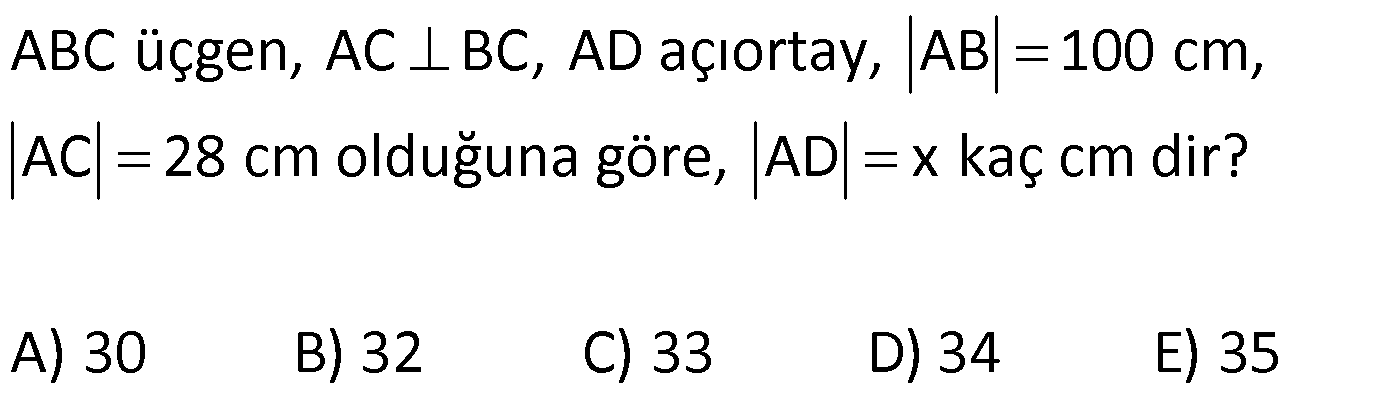
Çözüm için Tıklayınız.
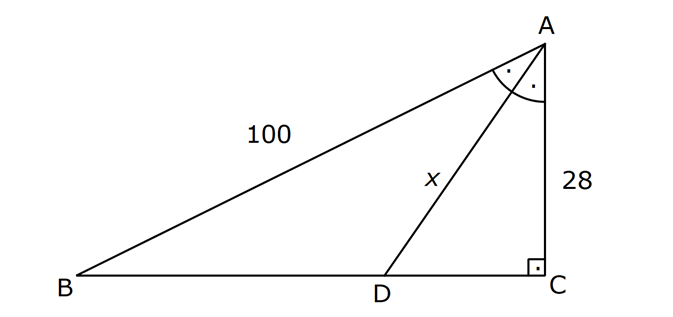
5.SORU
| | | | | |
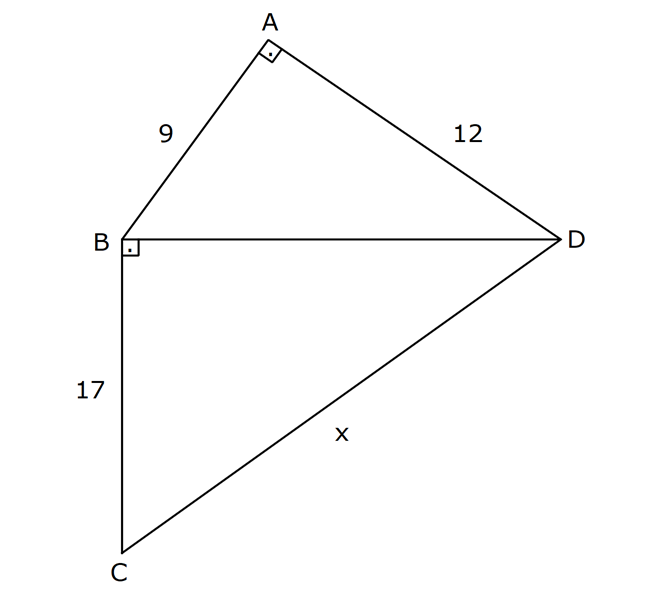
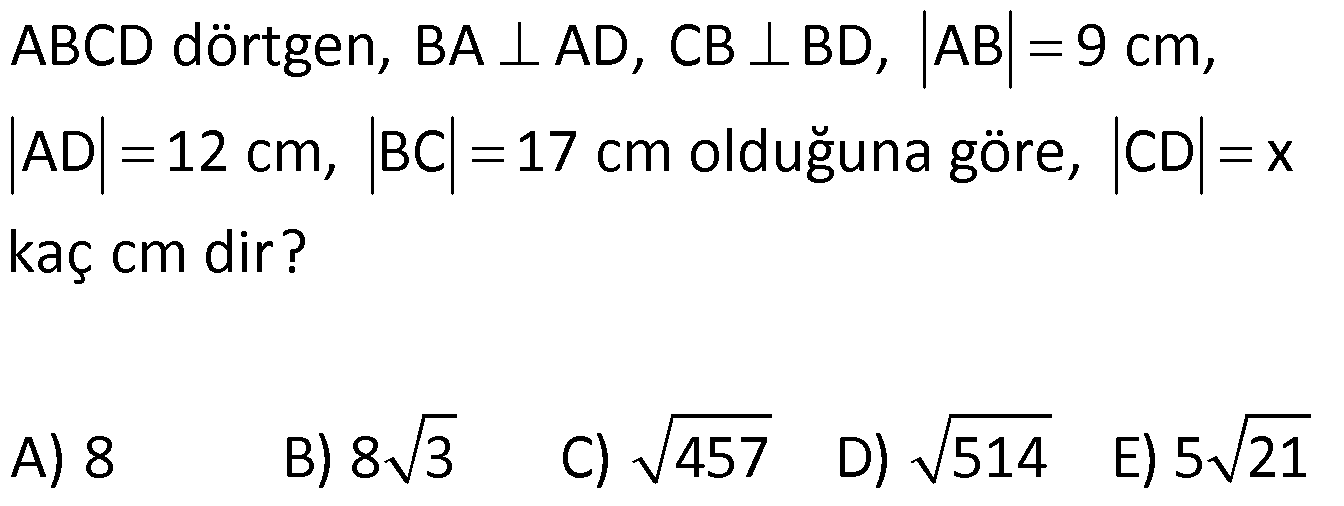
Çözüm için Tıklayınız.
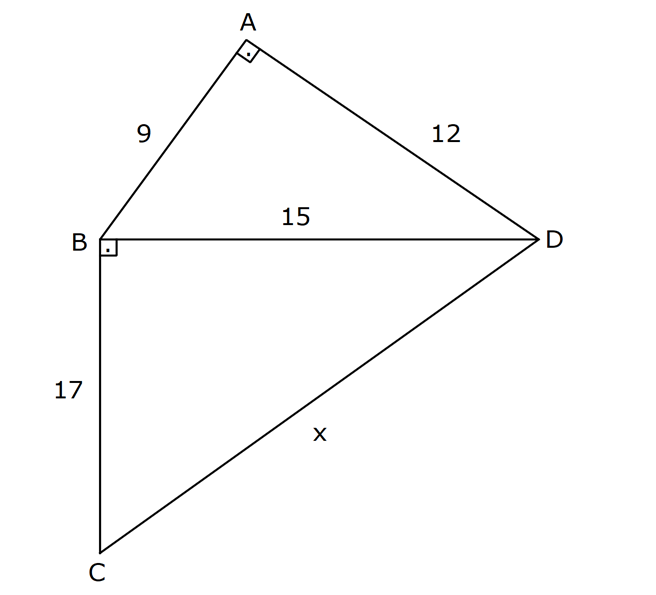
6.SORU
| | | | | |
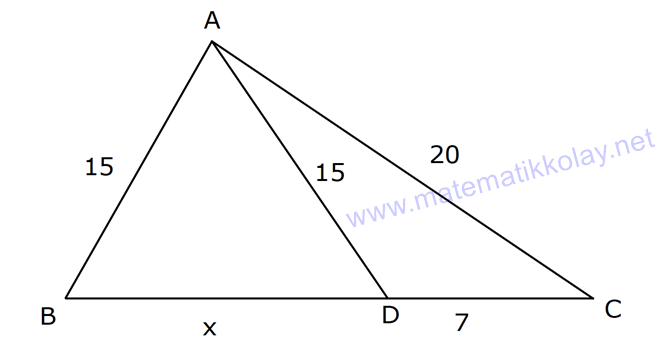
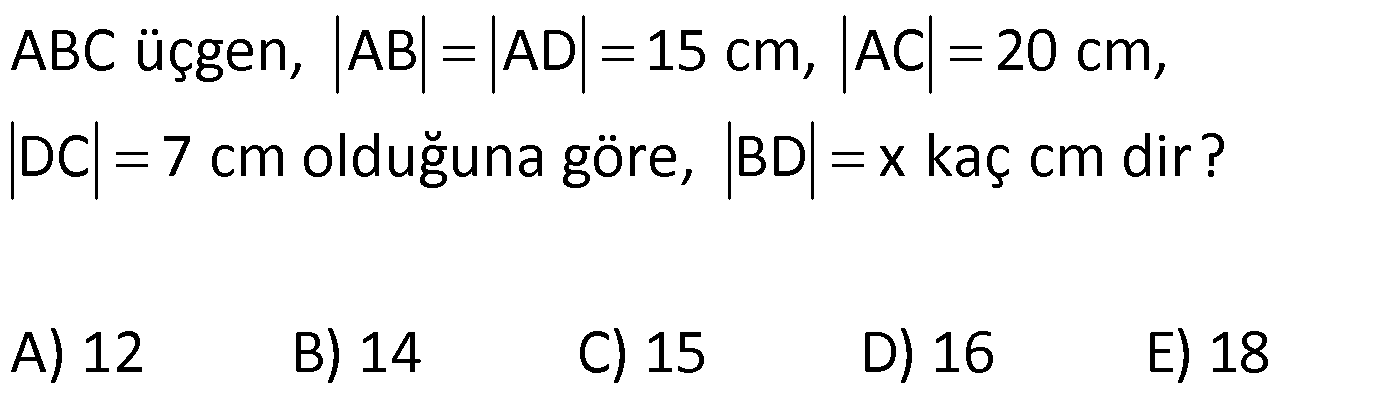
Çözüm için Tıklayınız.
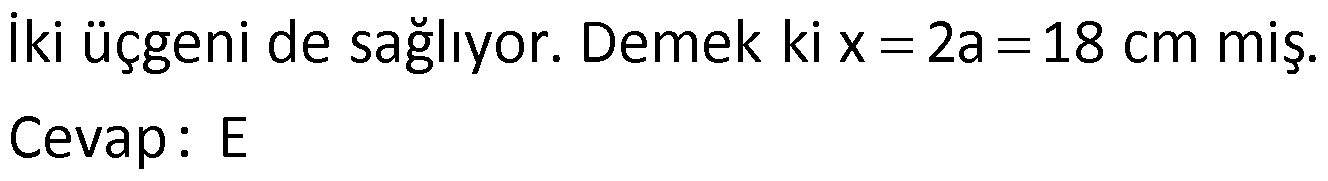
Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
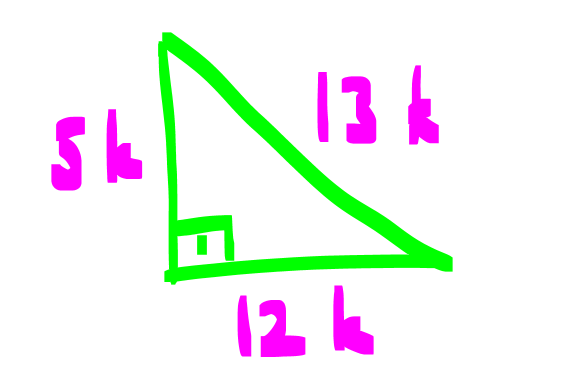
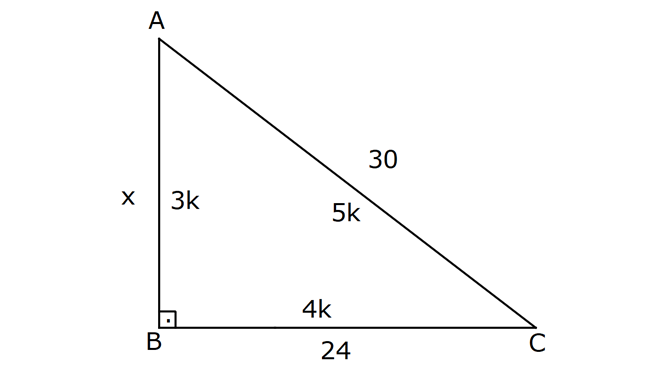
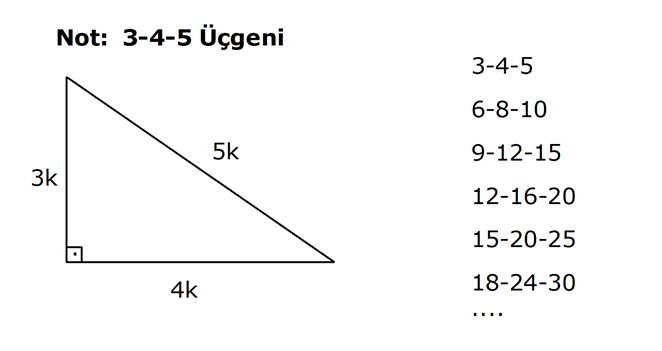
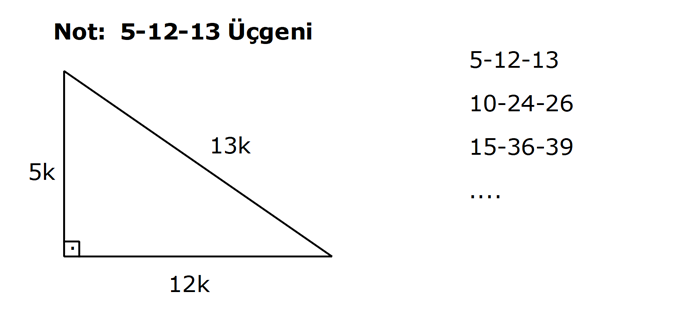
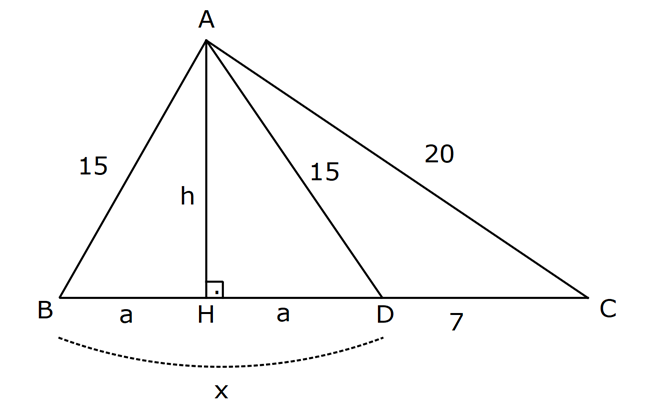
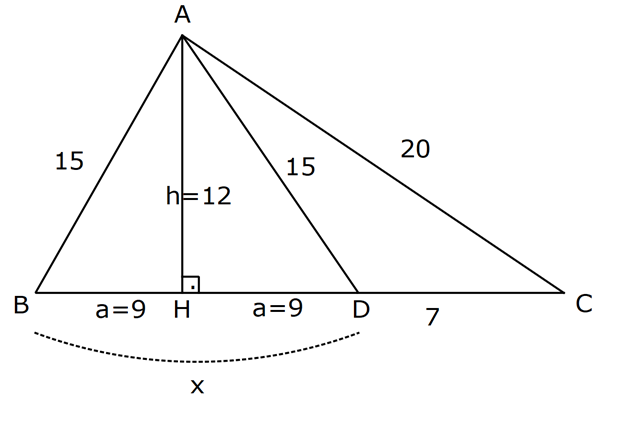
KENARLARINA GÖRE ÖZEL ÜÇGENLER www.matematikkolay.net 1) ABC üçgen AB BC BC 24 cm AC 30 cm AB x Yukarıda verilenlere göre, x kaç cm dir? A) 12 B) 15 C) 16 D) 18 E) 20 ÇÖZÜM: Pisagor yaparak x bulunabilir. Ancak, hioptenüs ve bir dik kenar arasında 5’e 4 oranında bir oran var. 3- 4 – 5 üçgeninin katlarıyla oluştuğunu düşünebiliriz. O halde, 4k 24 k 6 dır. x 3k 3.6 18 dir. Cevap: D 2) ABC üçgen AD 6 cm AC 8 cm BC 17 cm BD x Yukarıda verilenlere göre, x kaç cm dir? A) 9 B) 10 C) 12 D) 13 E) 14 ÇÖZÜM: ADC üçgeni bir 3k – 4k – 5k üçgenidir. O halde A açısı 90 dir. ABC üçgeni de bir dik üçgen oldu. Hipotenüsü 17 ve bir dik kenarı 8 cm. O halde bu bir 8 -15-17 üçgenidir. AB 15 cm olmalıdır. x 15 6 9 cm dir. Ce vap : A www.matematikkolay.net 3) ABC üçgen BA DC BC CA BC 24 cm AC 10 cm DC h Yukarıda verilenlere göre, x kaç cm dir? 60 80 120 125 130 A) B) C) D) E) 7 11 13 14 17 ÇÖZÜM: 2 ABC üçgeninin dik kenarları 5 ve 12 ile orantılıdır. O halde bu bir 5k -12k -13k üçgenidir. 5k 10 k 2 AB 13k 26 cm dir. 10. 24 A(ABC) 12 2 26 13 .h 2 120 13h 120 h cm dir. Cevap: C 13 4) ABC üçgen, AC BC, AD açıortay, AB 100 cm, AC 28 cm olduğuna göre, AD x kaç cm dir? A) 30 B) 32 C) 33 D) 34 E) 35 ÇÖZÜM: ABC üçgeninin hipotenüsü ise bir dik kenar arasında 100 25 28 7 25’e 7 şeklinde bir oran vardır. O halde bu bir 7k -24k -25k üçgenidir. k 4 tür. BC 24.4 96 cm dir. [AD] açıortayından dolayı BC uzunluğu 100 oranında bölünür. 28 100 25 28 7 3 BD BD 25a, DC 7a diyebiliriz. DC 25a 7a 96 32a 96 a 3 cm dir. DC 7a 7.3 21 cm dir. 21 ADC üçgeninin dik kenarları 3 28 4 7 3 oranındadır. 4 O halde bu bir 3k – 4k – 5k üçgenidir. k 7 dir. x 5k 35 cm buluruz. Cevap : E www.matematikkolay.net 5) ABCD dörtgen, BA AD, CB BD, AB 9 cm, AD 12 cm, BC 17 cm olduğuna göre, CD x kaç cm dir? A) 8 B) 8 3 C) 457 D) 514 E) 5 21 ÇÖZÜM: 3 2 2 ABD üçgeni bir 3k – 4k – 5k üçgenidir (k 3) BD 5k 15 cm dir. Ancak BCD üçgeni bir 8 -15-17 üçgeni değildir. Çünkü 17 olan uzunluk, hipotenüse ait değildir. Pisagor yaparak x’i hesaplayabiliriz. x 15 2 2 2 17 x 225 289 x 514 x 514 cm dir. Cevap : D 6) ABC üçgen, AB AD 15 cm, AC 20 cm, DC 7 cm olduğuna göre, BD x kaç cm dir? A) 12 B) 14 C) 15 D) 16 E) 18 ÇÖZÜM: www.matematikkolay.net 2 2 2 2 2 ABH üçgeni AHC üçgeni A’dan yükseklik indirerek, iki üçgenden de pisagor hesabı yapabiliriz. h 15 a 20 (a 7) Bu hesaptan a’yı buluruz. Ancak, ilk bakışta bildiğimiz özel üçgenleri test ederek bazen daha hızlı çözüme gidebiliriz. ABH üçgeninin hipotenüsü 15 cm. Belki 9-12-15 üçgeni olabilir. AHC üçgeninin de hipotenüsü 20 cm. Belki 12-16-20 üçgeni olabilir. Ortak uzunluk olan h’ye 12 cm diyerek, test edelim. İki üçgeni de sağlıyor. Demek ki x 2a 18 cm miş. Cevap: E
Meb te çalışan bir öğretmen olarak sizi geç keşfetmiş olmanın şaşkınlığı içindeyim. Emeğinize sağlık harika bir iş çıkarmışsınız. Alanım matematik değil ancak matematiği seven biri olarak öğrencilerime tavsiye ediyorum sizi. Nokta atışlarınız ve öğretmenlere kullanım için izin verdiğiniz için ayrıca teşekkür ederim.