Bu bölümde Kenar Orta Dikme ve Yükseklik ile ilgili 10 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
1.SORU
 |  |  |  |  |
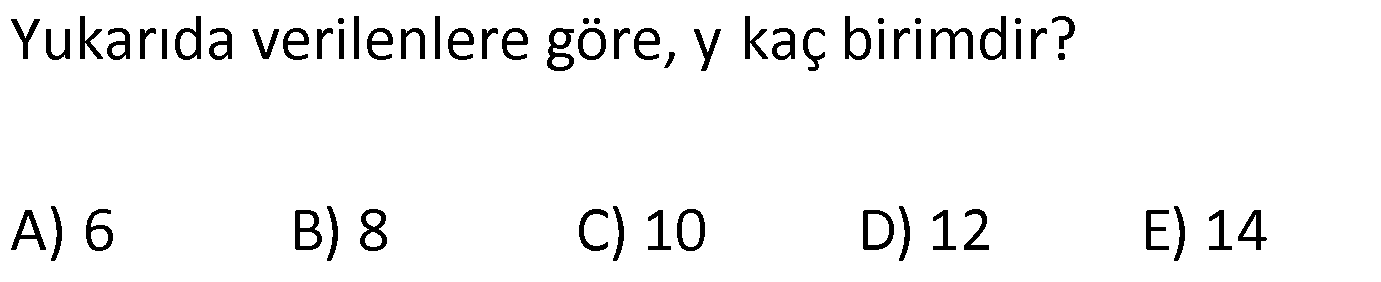
Çözüm için Tıklayınız.
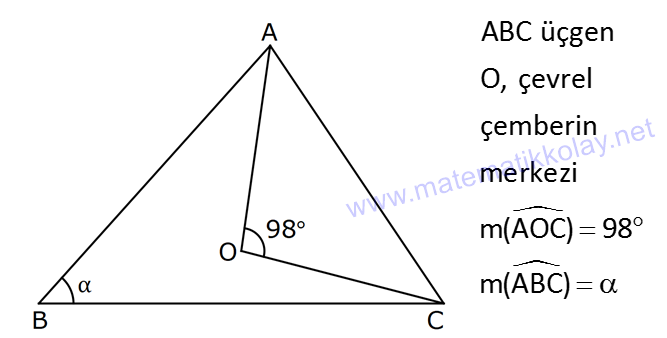
2.SORU
| | | | | |
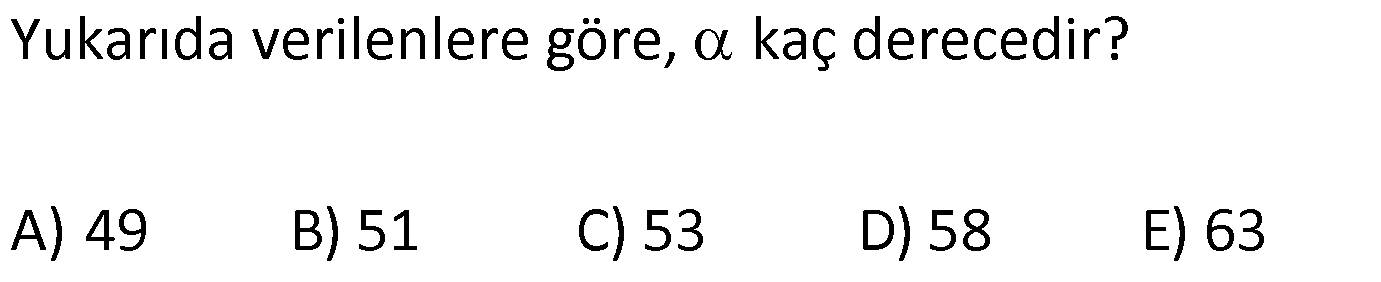
Çözüm için Tıklayınız.
3.SORU
| | | | | |
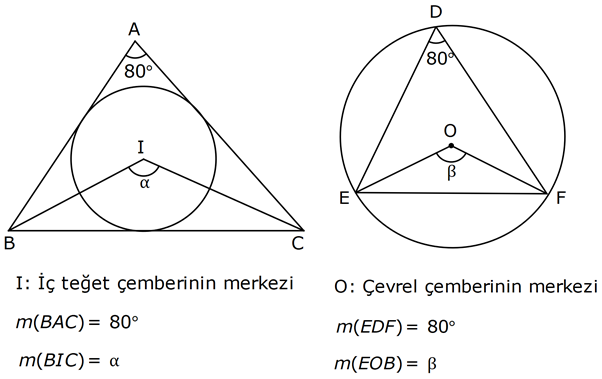
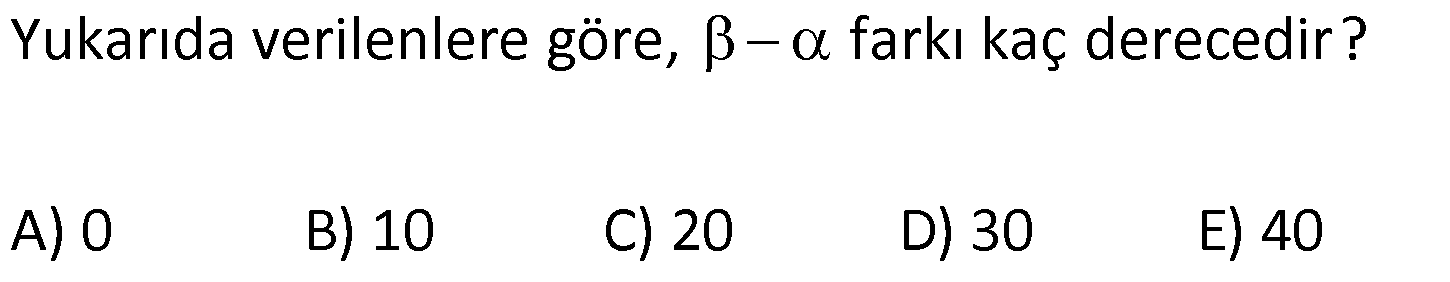
Çözüm için Tıklayınız.
4.SORU
| | | | | |
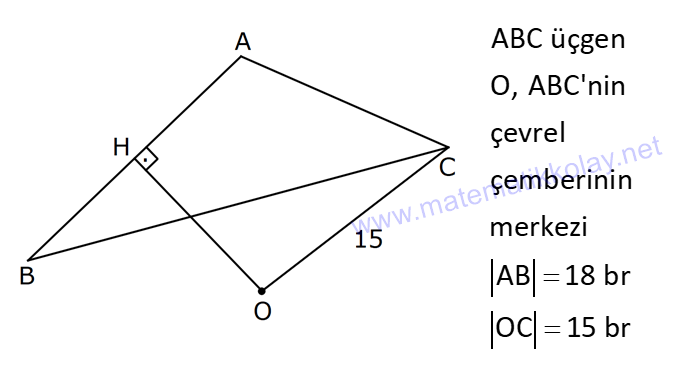
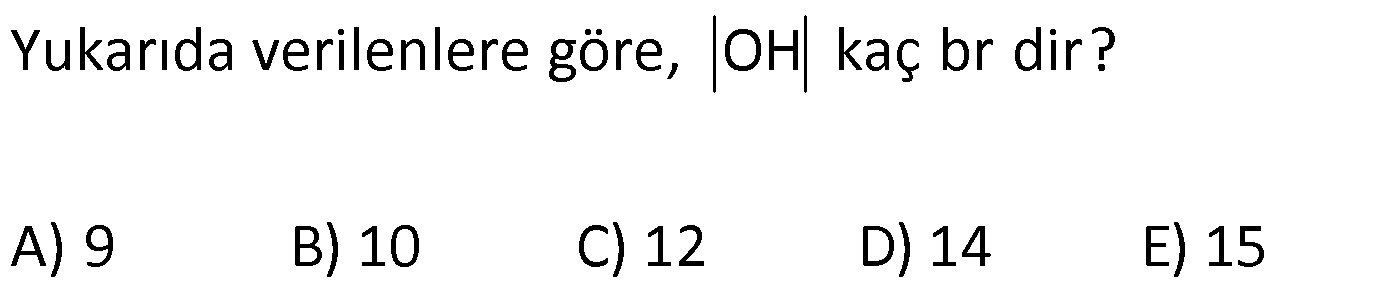
Çözüm için Tıklayınız.
5.SORU
| | | | | |
Çözüm için Tıklayınız.
6.SORU
| | | | | |
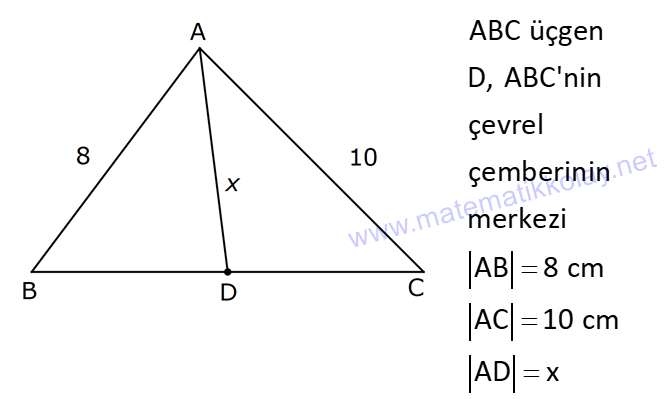
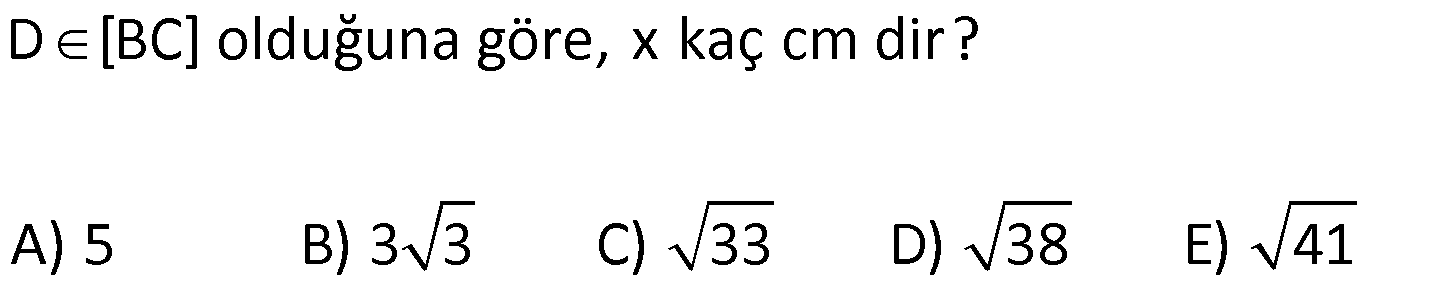
Çözüm için Tıklayınız.
7.SORU
| | | | | |
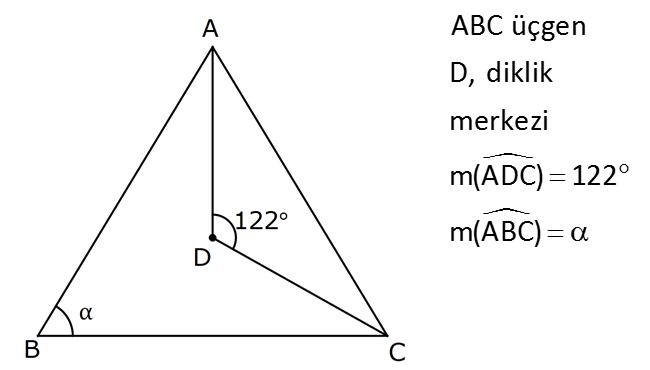
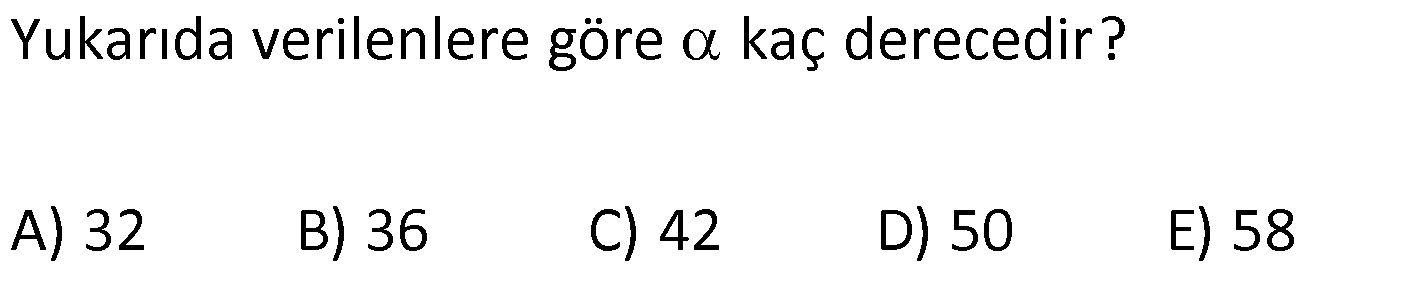
Çözüm için Tıklayınız.
8.SORU
| | | | | |
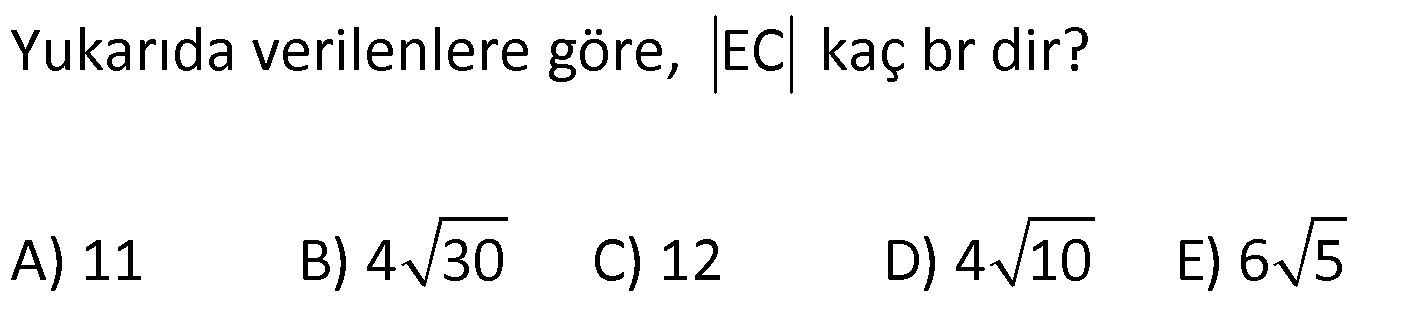
Çözüm için Tıklayınız.
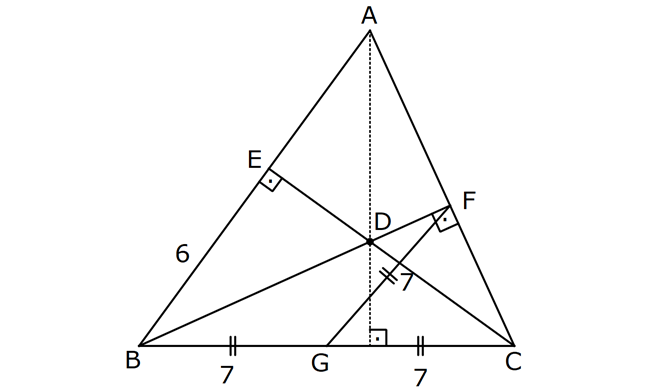
9.SORU
| | | | | |
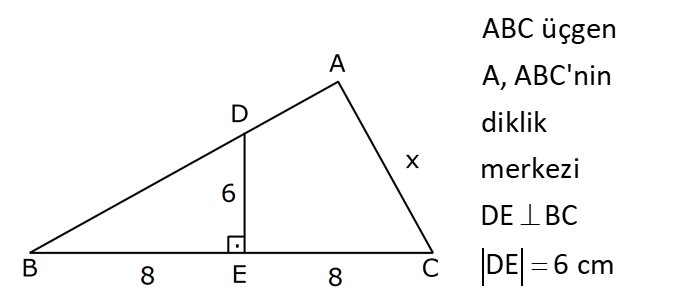
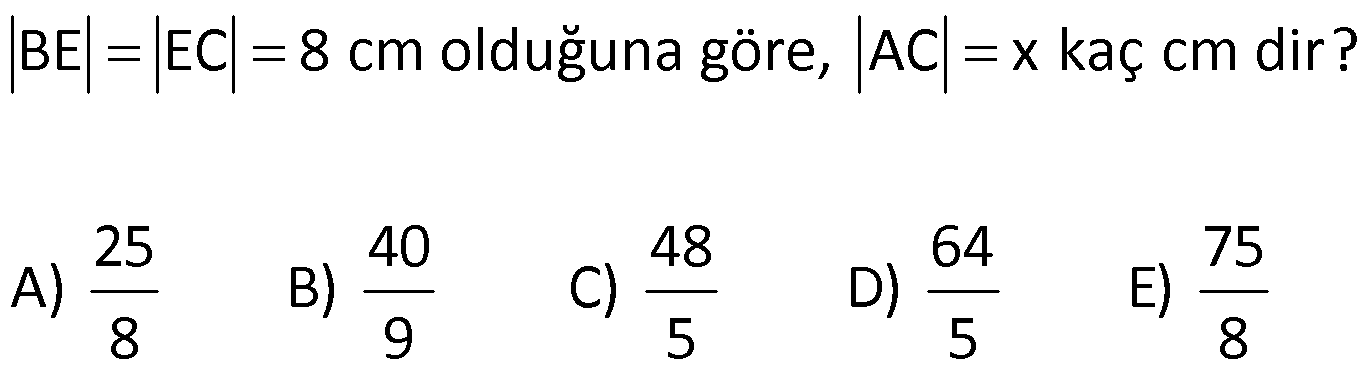
Çözüm için Tıklayınız.
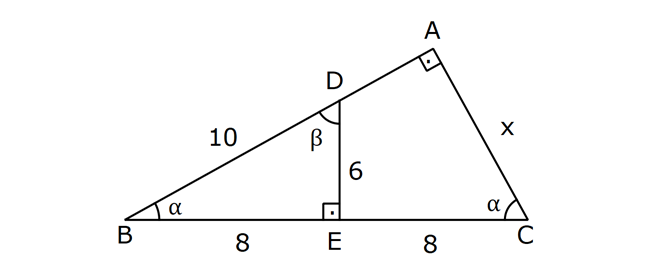
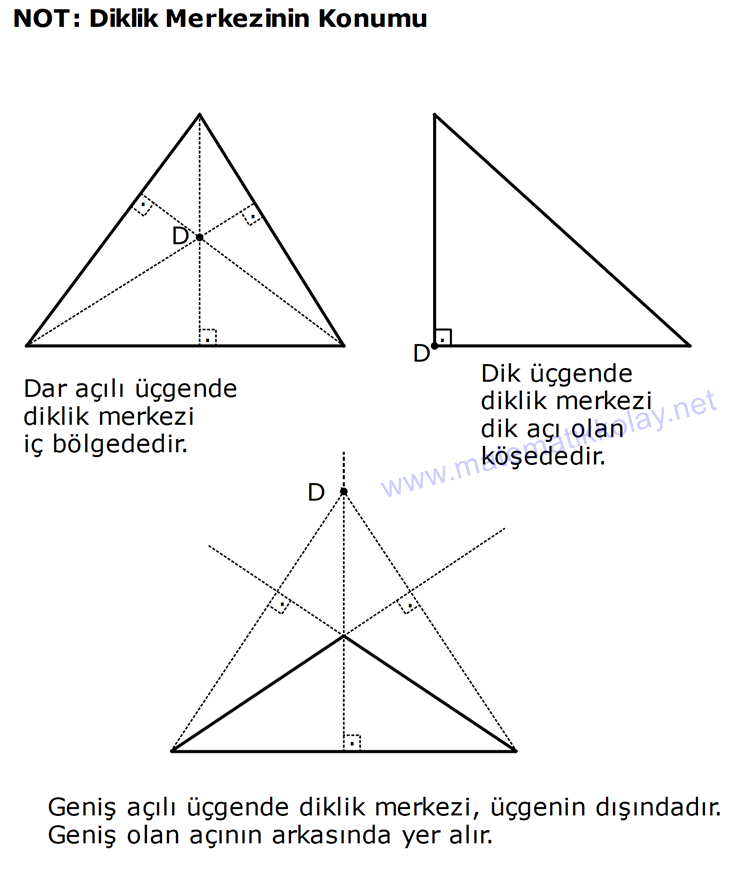
10.SORU
| | | | | |
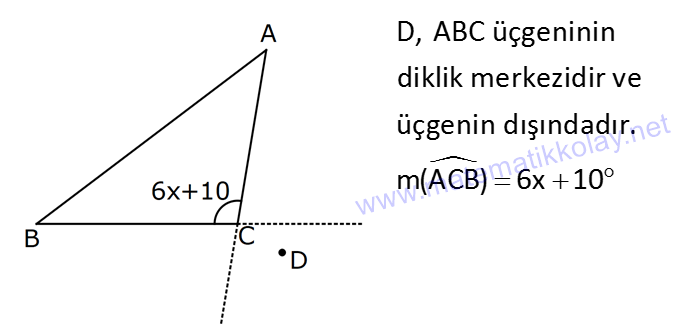
Çözüm için Tıklayınız.
Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
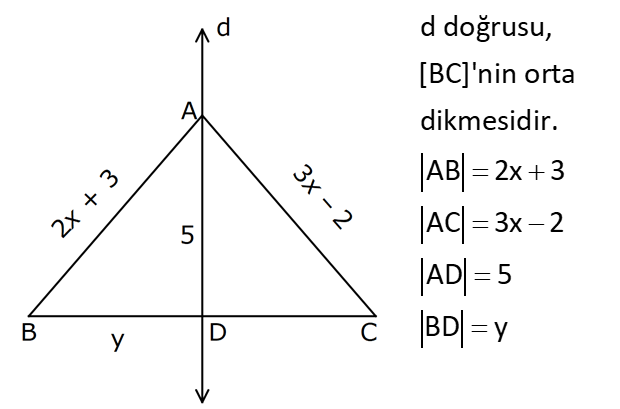
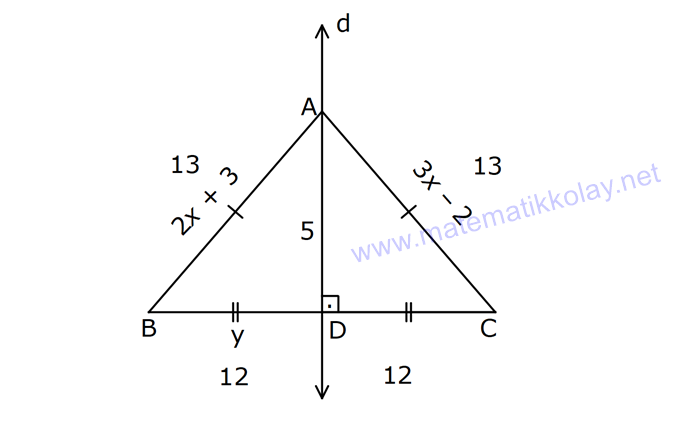
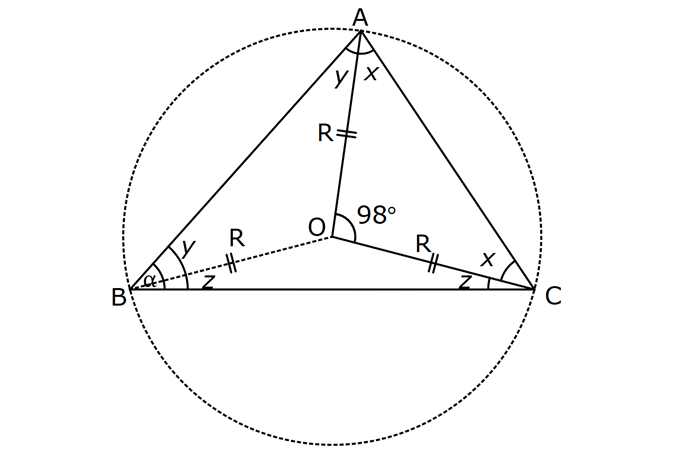
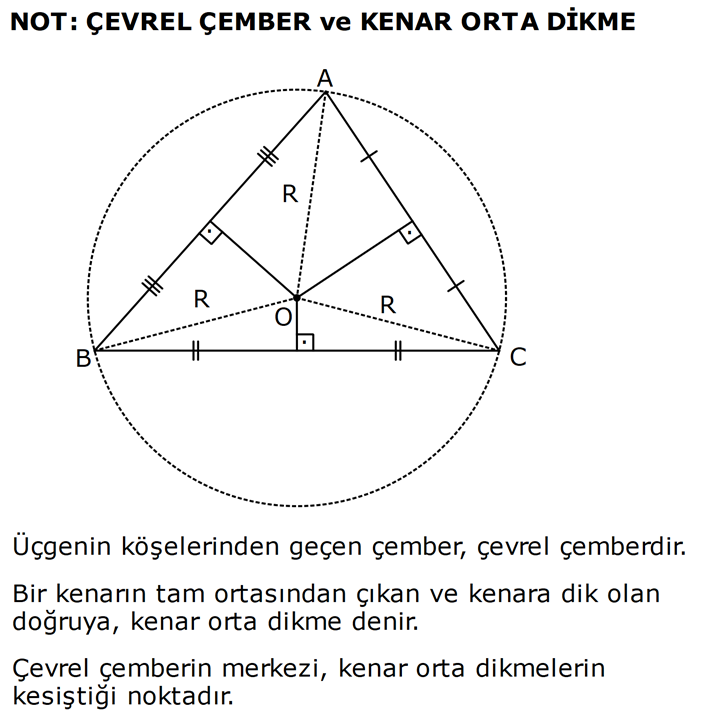
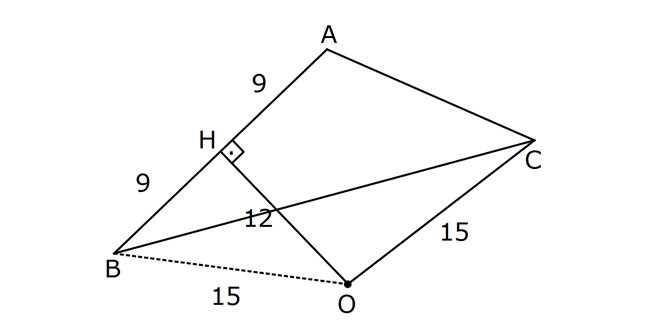
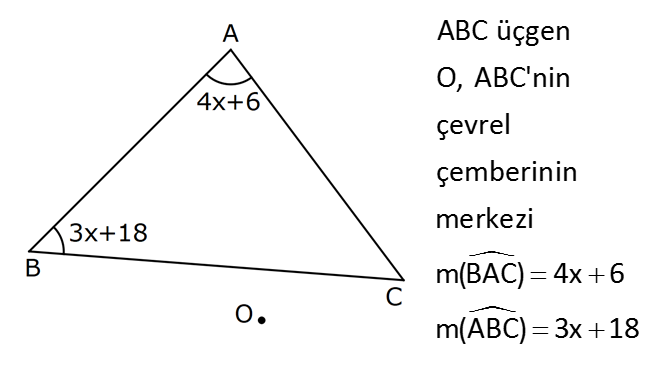
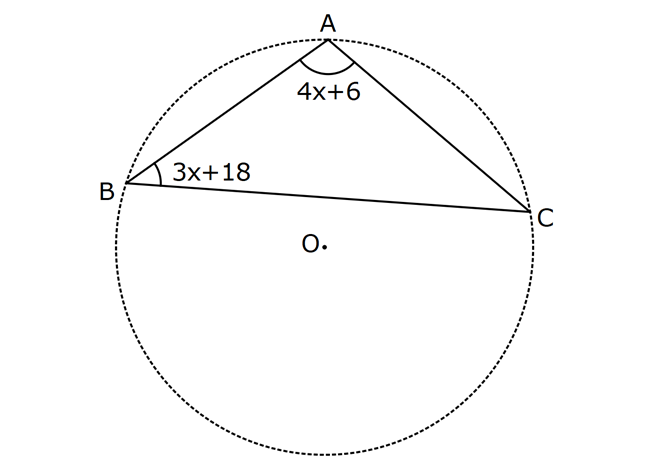
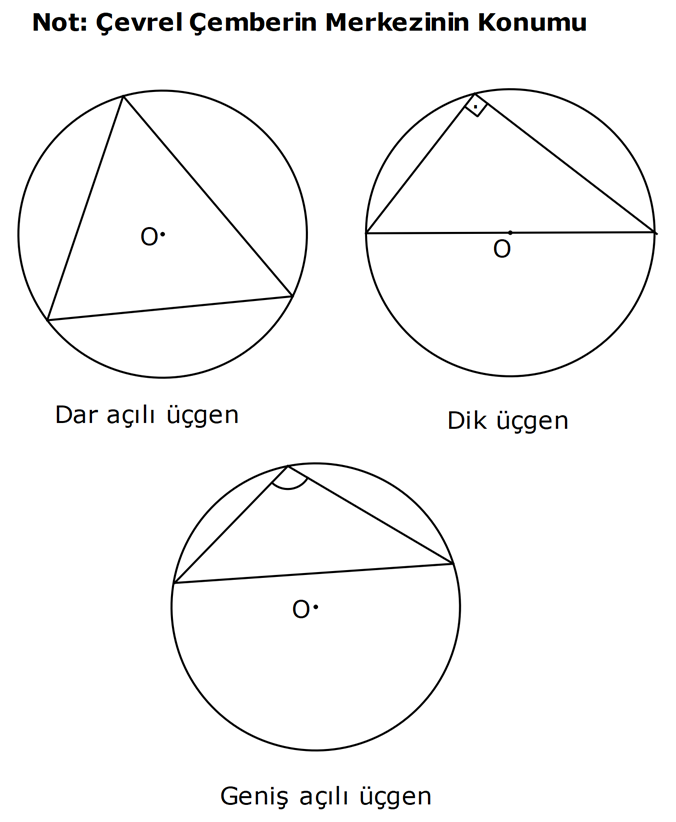
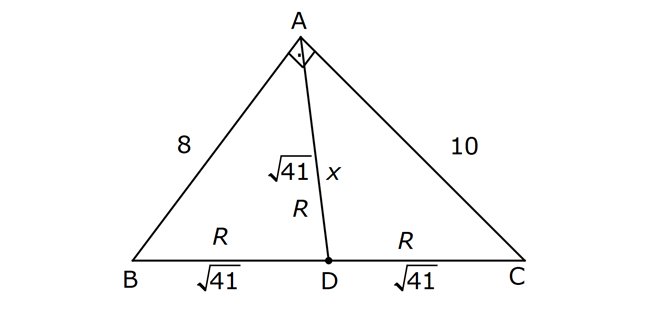
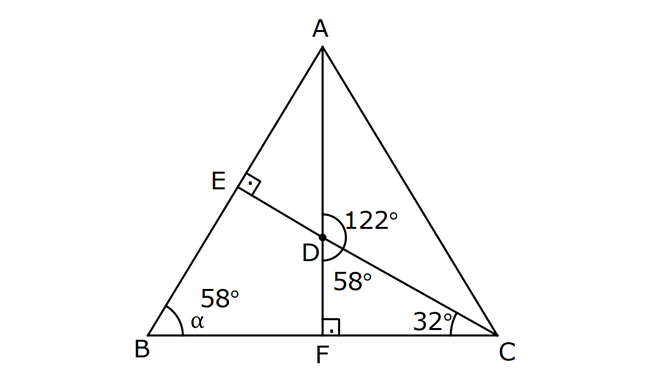
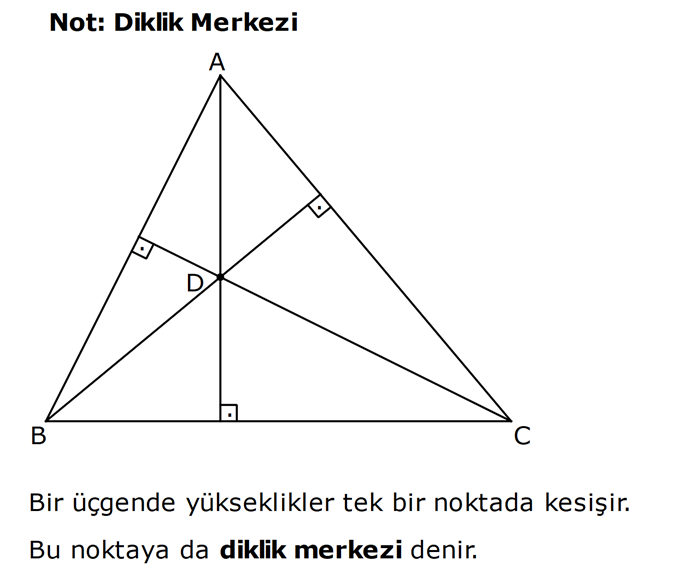
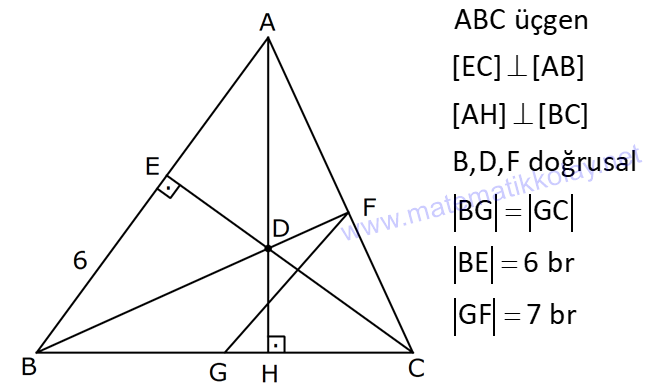
KENAR ORTA DİKME VE YÜKSEKLİK www.matematikkolay.net 1) d doğrusu, [BC]’nin orta dikmesidir. AB 2x 3 AC 3x 2 AD 5 BD y Yukarıda verilenlere göre, y kaç birimdir? A) 6 B) 8 C) 10 D) 12 E) 14 ÇÖZÜM: Bir doğru parçasının tam ortasını dik kesen doğruya orta dikme doğrusu denir. Orta dikmenin üstündeki herhangi bir noktadan, doğru parçasının uç noktalarına olan uzaklıklar birbirine eşittir. AB AC Not : 5 2x 3 3x 2 5 x tir. AB 2x 3 13 br dir. D açısı 90 olduğudan, ABD bir 5-12 -13 üçgenidir. y 12 br olur. Cevap : D 2) ABC üçgen O, çevrel çemberin merkezi m(AOC) 98 m(ABC) Yukarıda verilenlere göre, kaç derecedir? A) 49 B) 51 C) 53 D) 58 E) 63 ÇÖZÜM: O noktasının köşelere olan uzaklıkları birbirine eşittir. Çünkü hepsi, çevrel çemberin yarıçapıdır. ABC üçgeninin içinde 3 tane ikizkenar üçgen oluşur. Açıları x, y ve z diye isimlendirirsek, AOC üçgenin 41 e göre, x x 98 180 2x 82 x 41 olur. ABC üçgenine göre, 2x 2y 2z 180 x y z 90 dir. y z 49 dir 49 olur. Cevap: A Aynı yayı gören çevre açı, merkez açının yar II.Yol: (Çember Bilgisi Gerekli – 11.Sınıf) ısıdır. 98 49 dir. 2 www.matematikkolay.net 3) Yukarıda verilenlere göre, farkı kaç derecedir? A) 0 B) 10 C) 20 D) 30 E) 40 ÇÖZÜM: İç teğet çemberinin merkezi, iç açıortayların kesişim noktasıdır. İki iç açıortay arasındaki açıyı da A 90 ile buluyoruz. 2 80 90 90 40 130 dir. 2 Çevrel çemberinin merkezi, kenar orta dikmelerin kesi ştiği noktadır. Pratik olarak 2.80 160 dir , diyebiliriz (Aynı yayı gören çevre açı, merkez açının yarısıdır.). Veya ilk soruda olduğu gibi, ikizkenar üçgenler yardımıyla 160 yi bulabiliriz. Buna göre , 160 130 30 dir. Cevap: D 4) ABC üçgen O, ABC’nin çevrel çemberinin merkezi AB 18 br OC 15 br Yukarıda verilenlere göre, OH kaç br dir? A) 9 B) 10 C) 12 D) 14 E) 15 ÇÖZÜM: www.matematikkolay.net O noktasının köşelere olan uzaklıkları, birbirine eşit – tir. BO 15 br olur. Ayrıca H noktası, AB’nin orta noktasıdır. Çevrel çemberin merkezi, kenarorta dikmelerin kesişim noktasıdır. BH 9 br dir. OBH 3 3 3 üçgeni bir 9 -12 -15 üçgenidir (3k – 4k – 5k) OH 12 br buluruz. Cevap : C 5) ABC üçgen O, ABC’nin çevrel çemberinin merkezi m(BAC) 4x 6 m(ABC) 3x 18 O noktası, şekildeki gibi ABC üçgeninin dışında olduğuna göre, x’in derece olarak alabileceği tam sayı değeri kaçtır? A) 21 B) 22 C) 23 D) 24 E) 25 ÇÖZÜM: Çevrel çemberin merkezi, üçgenin dışında ise bu üçgen geniş açılı bir üçgendir. Çemberin merkezini gören açı, geniş açıdır. 4x 6 90 4x 84 x 21 dir. Bir üçgende iki geniş açı olamaz. Bu sep eble, 3x 18 90 3x 72 x 24 dir. x 22 veya 23 olabilir. Ancak A ile B açılarının toplamı 7x 24 tür. x 23 olursa toplamları 7.23 24 185 olur. Bu sebeple x sadece 22 olabilir. Cevap : B 6) ABC üçgen D, ABC’nin çevrel çemberinin merkezi AB 8 cm AC 10 cm AD x D [BC] olduğuna göre, x kaç cm dir? A) 5 B) 3 3 C) 33 D) 38 E) 41 ÇÖZÜM: www.matematikkolay.net 2 2 2 2 2 Çevrel çemberinin merkezi, bir kenarın üstünde ise o kenar hipotenüstür. Bunu gören açı da 90 dir. Yukarıdaki gibi muhteşem üçlüyü oluşturur. Pisagordan, BC 8 10 BC 64 100 BC 164 BC 164 4.41 2 41 cm dir . x 41 cm olur. Cevap : E 7) ABC üçgen D, diklik merkezi m(ADC) 122 m(ABC) Yukarıda verilenlere göre kaç derecedir? A) 32 B) 36 C) 42 D) 50 E) 58 ÇÖZÜM: Diklik merkezi, yüksekliklerin kesişim noktasıdır. AD ve CD yi şekildeki gibi uzatırsak, E ve F noktasında 90 lik açı oluştururlar. m(FDC) 180 122 58 dir. FCD üçgeninin iç açılarından, m(FCD) 180 5 8 90 32 dir. EBC üçgeninin iç açılarından, 180 90 32 58 dir. Cevap : E 8) ABC üçgen [EC] [AB] [AH] [BC] B,D,F doğrusal BG GC BE 6 br GF 7 br Yukarıda verilenlere göre, EC kaç br dir? A) 11 B) 4 30 C) 12 D) 4 10 E) 6 5 ÇÖZÜM: www.matematikkolay.net İki yükseklik D noktasında kesişmiş. Demek ki D noktası, diklik merkezidir. Buna göre, [BF] doğru parçası da yüksekliktir. F noktasında 90 açı oluşur. BG GC olduğundan, burada muhteşem üçlü oluşur. 2 2 2 2 2 BG GC GF 7 br dir. EBC üçgeninde pisagor yaparsak, 6 EC 14 36 EC 196 EC 160 EC 16.10 4 10 br olur. Cevap : D 9) ABC üçgen A, ABC’nin diklik merkezi DE BC DE 6 cm BE EC 8 cm olduğuna göre, AC x kaç cm dir? 25 40 48 64 75 A) B) C) D) E) 8 9 5 5 8 ÇÖZÜM: A noktası diklik merkezi ise, A açısı 90 dir. BDE üçgeni de bir 6 – 8 -10 üçgenidir. İç açılarına ve dersek, ABC üçgeni ile EBD üçgeninin benzer olduğunu görürüz. Buna göre, ABC 10 EBD 5 6 16 3 48 5x 48 x cm dir. x 5 Cevap: C 10) D, ABC üçgeninin diklik merkezidir ve üçgenin dışındadır. m(ACB) 6x 10 Yukarıda verilenlere göre, x’in alabileceği tam sayı değerleri kaç tanedir? A) 12 B) 15 C) 19 D) 22 E) 28 www.matematikkolay.net ÇÖZÜM: Diklik merkezi, C açısının arkasında kalmış. Buna göre, C açısı geniş açıdır. Buna göre, 6x 10 90 dir. 6x 80 3x 40 x tam sayı olarak en az 14 olabilir. Üçgenin iç açıları toplamı 180 olduğundan, 6x 10 180 dir. 6x 170 3x 85 x tam sayı olarak en fazla 28 olabilir. 14’ten 28’e kadar terim sayısı 28 14 1 15 tir. Demek ki x, 15 farklı tam sayı değeri alabilir. Cevap : B
