Bu bölümde Karede Açı ve Uzunluk ile ilgili 21 adet soru bulunmaktadir. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eger soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
1.SORU
 |  |  |  |  |
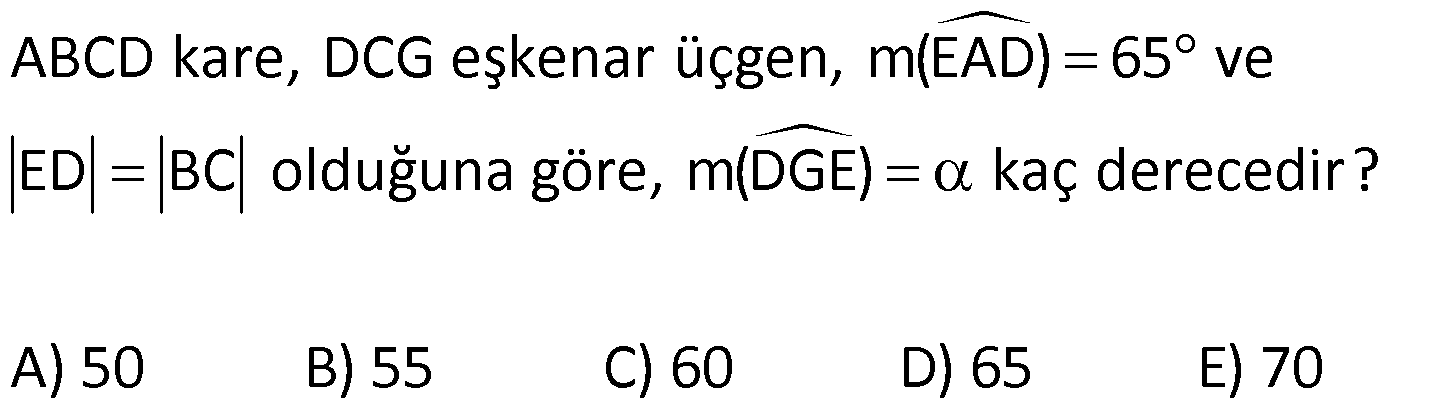
Çözüm için Tıklayınız.
2.SORU
| | | | | |
Çözüm için Tıklayınız.
3.SORU
| | | | | |
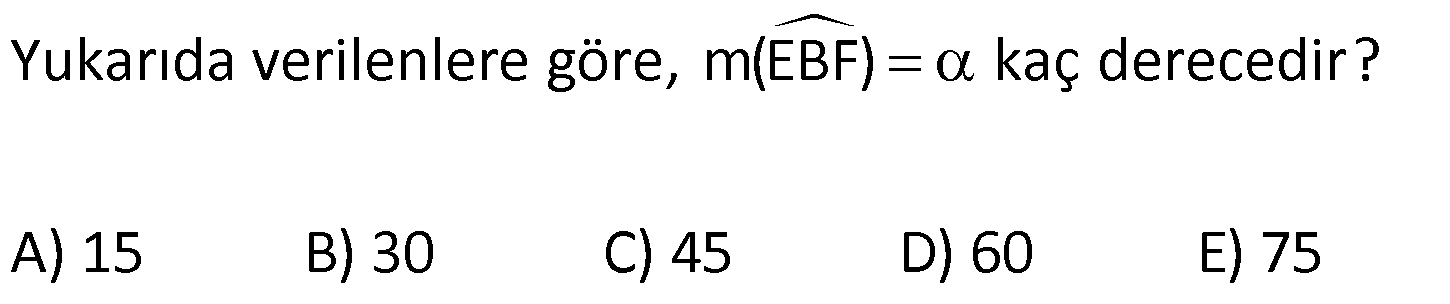
Çözüm için Tıklayınız.
4.SORU
| | | | | |
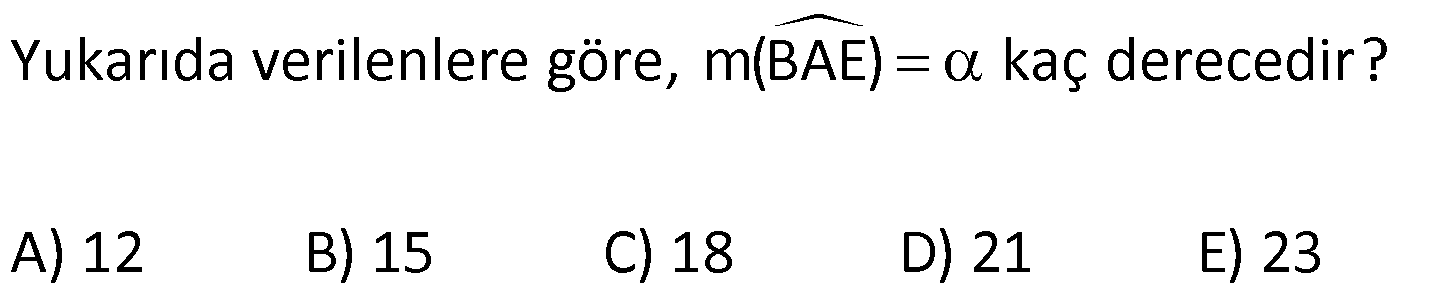
Çözüm için Tıklayınız.
5.SORU
| | | | | |
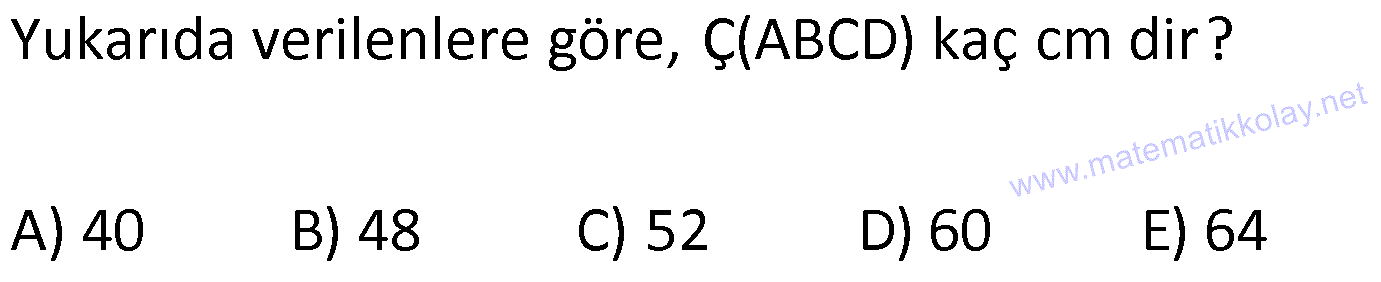
Çözüm için Tıklayınız.
6.SORU
| | | | | |
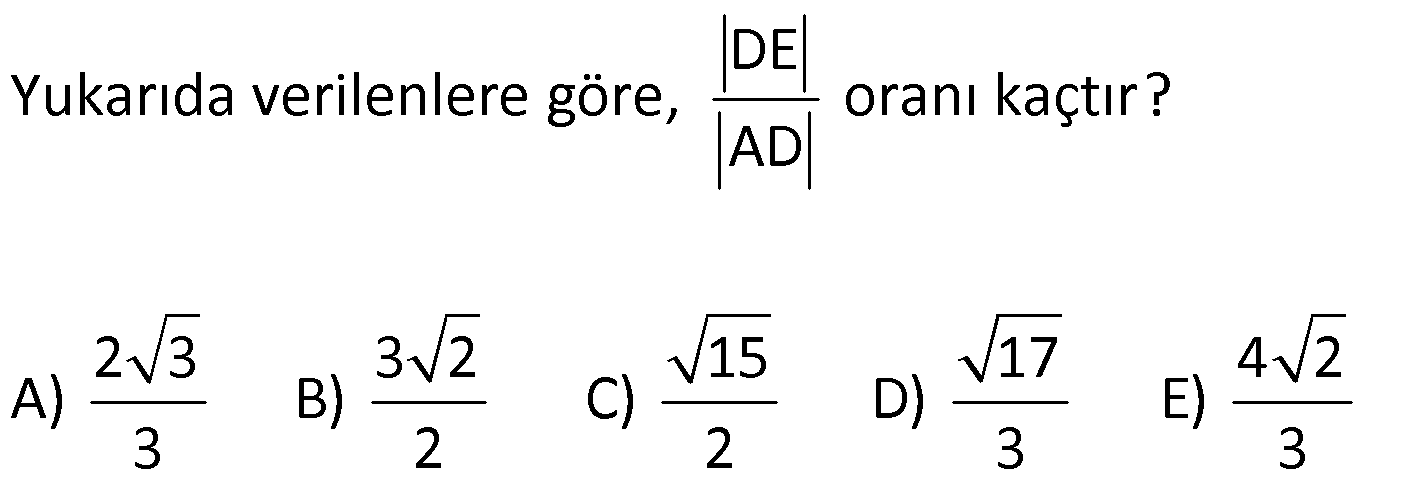
Çözüm için Tıklayınız.
7.SORU
| | | | | |
Çözüm için Tıklayınız.
8.SORU
| | | | | |
Çözüm için Tıklayınız.
9.SORU
| | | | | |
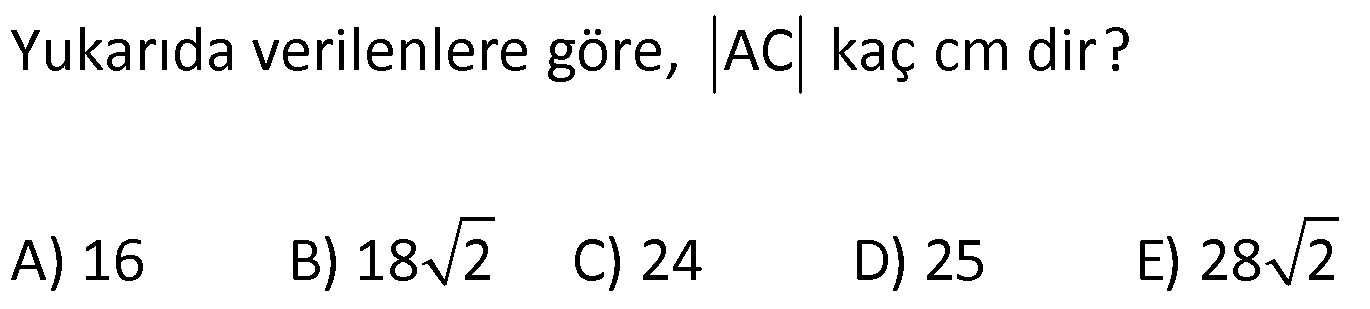
Çözüm için Tıklayınız.
10.SORU
| | | | | |
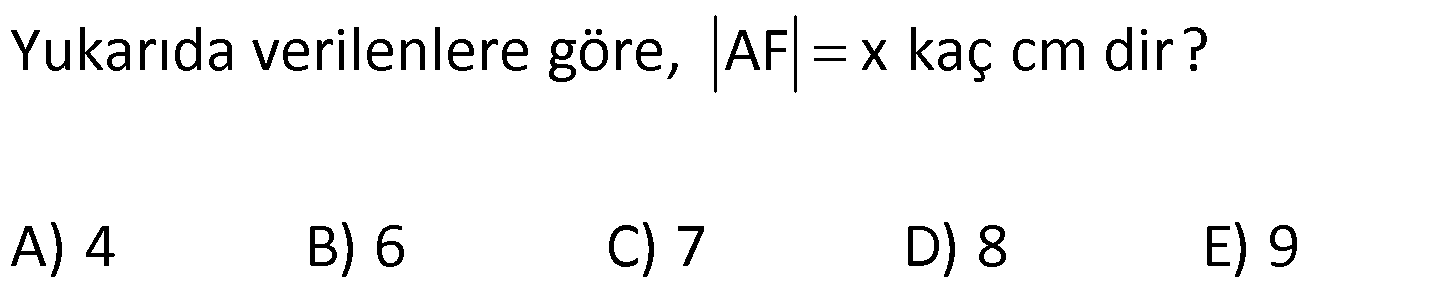
Çözüm için Tıklayınız.
Eger sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanin en altinda yer alan “Yorum Yap” seçenegi ile bunlari anlik olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
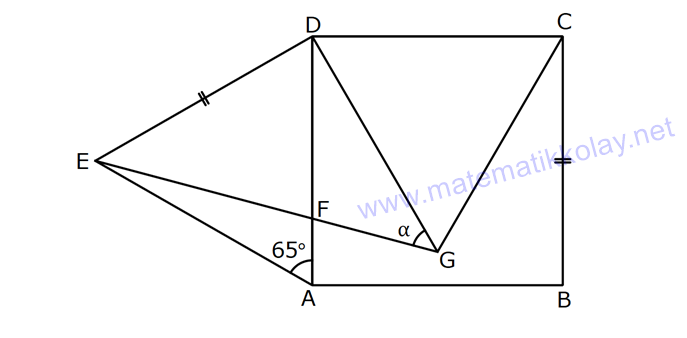
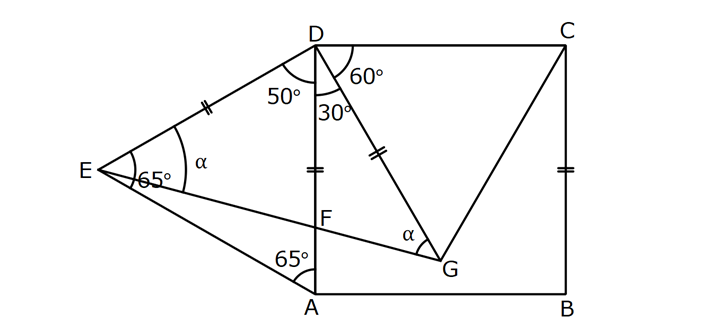
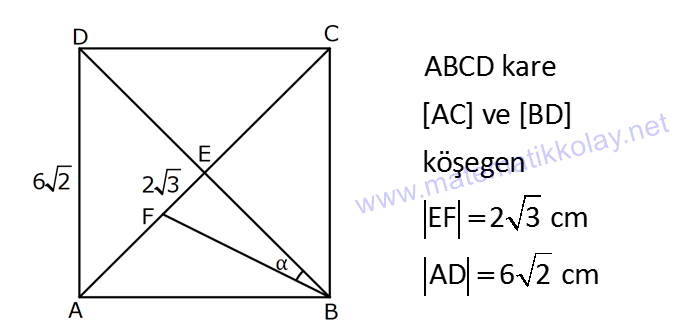
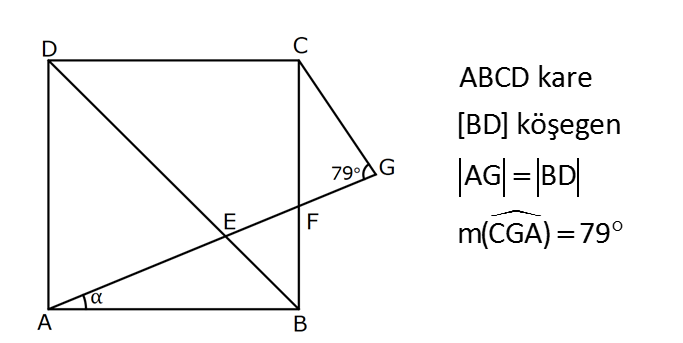
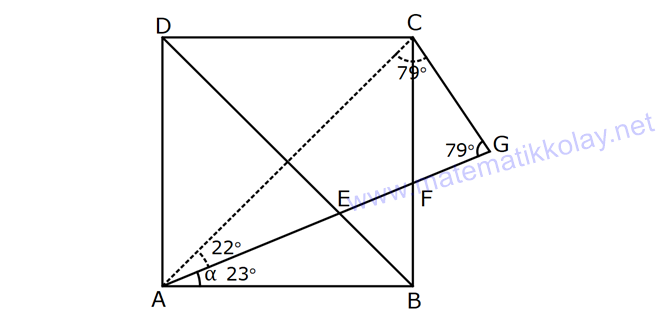
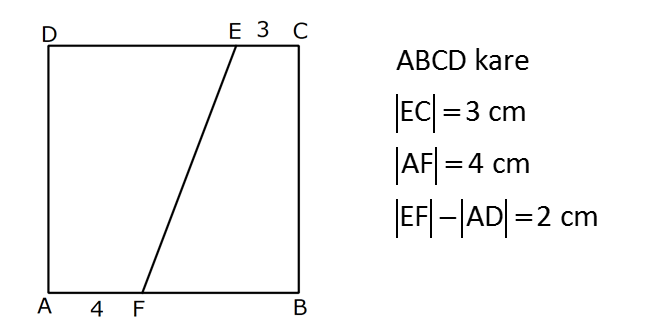
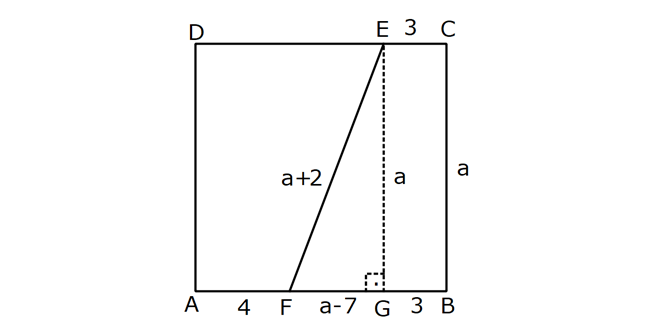
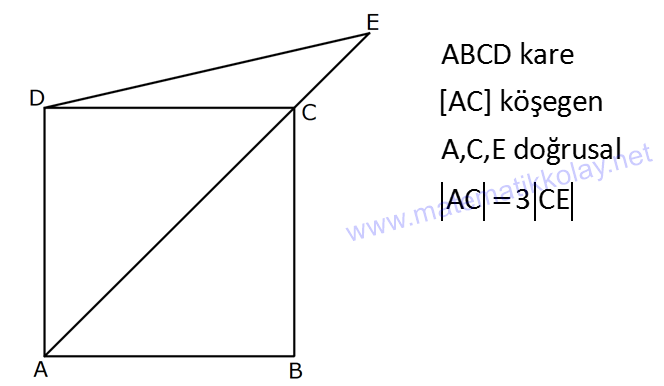
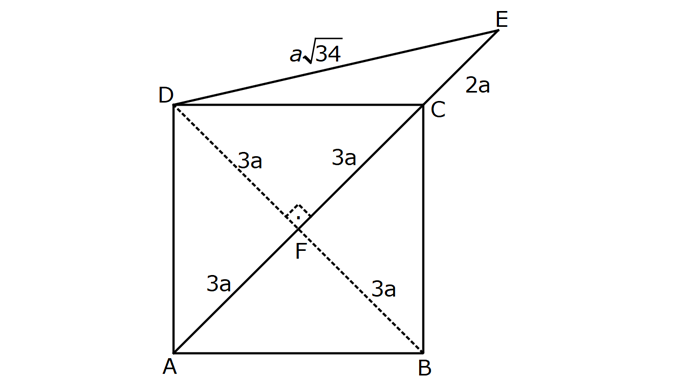
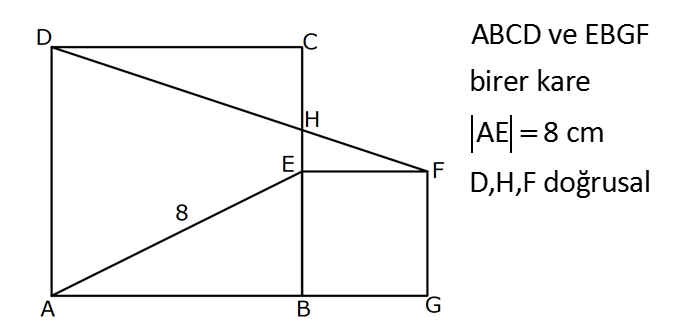
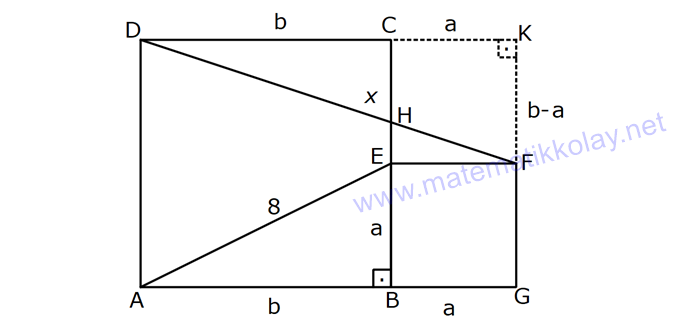
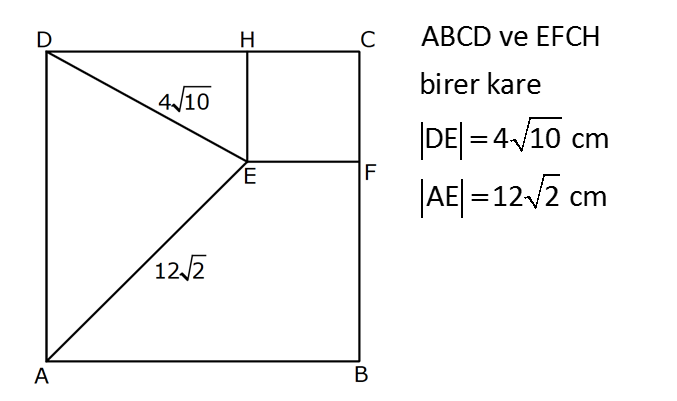
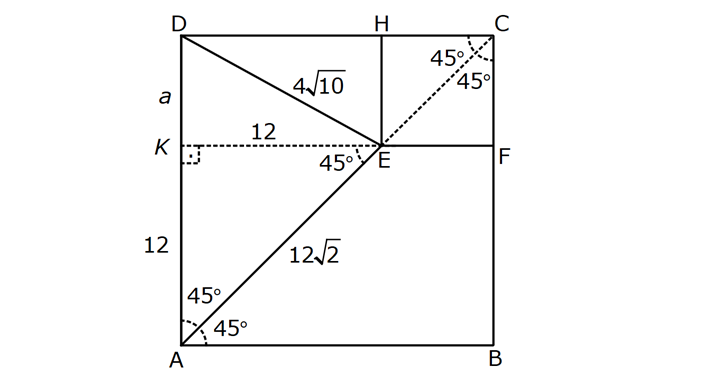
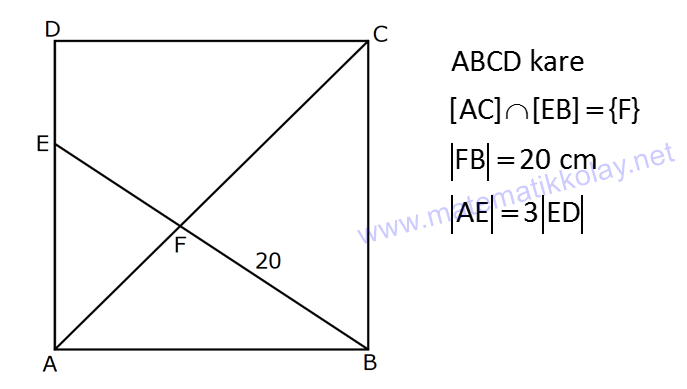
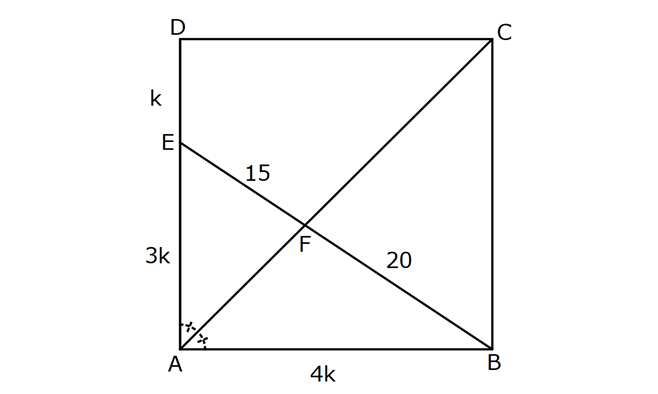
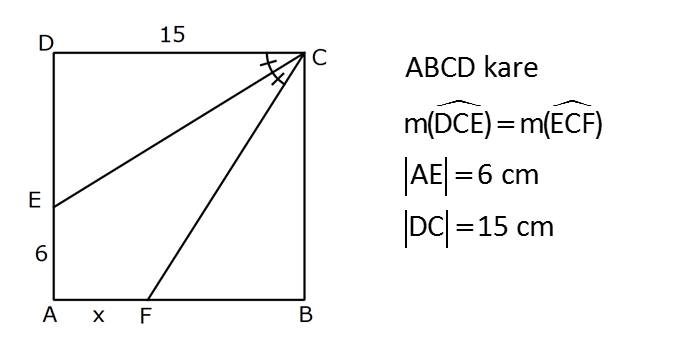
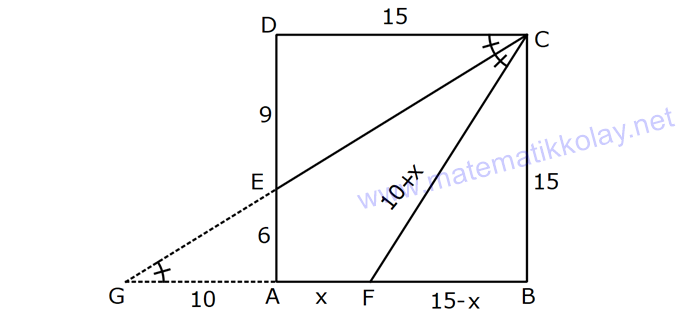
Karede Açı UZUNLUK www.matematikkolay.net 1) ABCD kare, DCG eşkenar üçgen, m(EAD) 65 ve ED BC olduğuna göre, m(DGE) kaç derecedir? A) 50 B) 55 C) 60 D) 65 E) 70 ÇÖZÜM: Tüm kenarları eşit dikdörtgene denir. ED AD olur. Bu nedenle EDA üçgeni ikizkenar üçgendir. m(AED) 65 dir. m(EDA) 180 65 65 50 olur. DCG üçgeni eşkenar üçgen olduğu için tüm iç açıla Not: kare rı 60 dir. Bu nedenle m(GDF) 90 60 30 olur. m(EDG) 50 30 80 olur. DCG eşkenar üçgeninin kenarları da karenin kenarı – na eşit olduğu için EDG üçgeni de ikizkenar olur. 80 180 2 100 50 buluruz. Cevap : A 2) Çevresi 24 cm olan bir karenin bir köşegeni kaç cm dir? A) 6 B) 6 2 C) 6 3 D) 9 E)12 ÇÖZÜM: 24 Bir kenarı 6 cm dir. 4 Karenin bir kenarı a br ise, köşegeni a 2 br dir. Buna göre, karenin köşegeni 6 2 br dir. Cevap: B Not: 3) ABCD kare [AC] ve [BD] köşegen EF 2 3 cm AD 6 2 cm Yukarıda verilenlere göre, m(EBF) kaç derecedir? A) 15 B) 30 C) 45 D) 60 E) 75 ÇÖZÜM: www.matematikkolay.net Karenin köşegenleri birbirini dik ortalar. Aynı zamanda açıortaydırlar (45 ,45 bölerler). Buna göre, m(BEF) 90 dir. BD 6 2. 2 12 cm dir. 12 BE 6 cm dir. 2 6 sayısı, 2 3’ün 3 katıdır ve E açısı 90 Not: dir. O halde, BEF üçgeni bir 30 – 60 – 90 üçgenidir. 30 buluruz. Cevap : B 4) ABCD kare [BD] köşegen AG BD m(CGA) 79 Yukarıda verilenlere göre, m(BAE) kaç derecedir? A) 12 B) 15 C) 18 D) 21 E) 23 ÇÖZÜM: Karede köşegen uzunlukları birbirine eşittir. Bu sebeple AC BD dir. O halde, ACG üçgeni ikizkenar üçgen olur. m(CAG) 180 79 79 22 dir. Karede köşegenler, 90 lik açıyı iki eş parçaya böler. Bu sebeple 45 22 23 dir. Cevap : E 5) ABCD kare EC 3 cm AF 4 cm EF AD 2 cm Yukarıda verilenlere göre, Ç(ABCD) kaç cm dir? A) 40 B) 48 C) 52 D) 60 E) 64 ÇÖZÜM: 2 2 2 2 Karenin bir kenarına a cm diyelim. EF a 2 cm olur. E’den dikme indirelim. FG a 3 4 a 7 cm olur. EFG üçgeninde pisagor yaparsak, (a 2) a (a 7) a 2 4a 4 a 2 2 ( 15).( 3) (a 3 cm olamaz. Çünkü FG a 7 değeri 0 ‘ dan büyüktür.) a 14a 49 0 a 18a 45 0 (a 15)(a 3) a 15 cm dir. Ç(ABCD) 4.15 60 cm dir. Cevap : D www.matematikkolay.net 6) ABCD kare [AC] köşegen A,C,E doğrusal AC 3 CE DE Yukarıda verilenlere göre, oranı kaçtır? AD 2 3 3 2 15 17 4 2 A) B) C) D) E) 3 2 2 3 3 ÇÖZÜM: 6a 2a 2 2 2 2 2 2 AC 3 CE CE 2a dersek, AC 6a olur. [BD] köşegenini çizdiğimizde, iki köşegen dik kesişir ve birbirini ortalar. Yani her bir parça 3a olur. DFC üçgeninde pisagor yaparsak, DE (3a) (5a) DE 9a 25a D 2 2 E 34a DE a 34 olur. DFA üçgeni, 45- 45- 90 üçgeni olduğundan AD 3a 2 dir. Buna göre, DE a AD 34 3:00 ÖÖ 17 buluruz. Cevap : D 2 3 7) ABCD ve EBGF birer kare AE 8 cm D,H,F doğrusal Yukarıdaki verilere göre, DF kaç cm dir? A) 8 2 B) 8 3 C) 12 D) 16 E) 8 5 ÇÖZÜM: 2 2 2 2 2 2 2 Küçük karenin bir kenarına a, büyük karenin bir ke – narına ise b diyelim. ABE üçgenindeki pisagora göre, a b 64 tür. DKF üçgenindeki pisagora göre, x (b a) (b a) x b 2ab 2 2 a b 2ab 2 2 2 2 2 2 2 64 2 a x 2a 2b x 2(a b ) x 128 x 8 2 cm dir. Cevap : A 8) www.matematikkolay.net ABCD ve EFCH birer kare DE 4 10 cm AE 12 2 cm Yukarıda verilenlere göre, küçük karenin bir kenarı kaç cm dir? A) 3 B) 4 C) 5 D) 6 E) 7 ÇÖZÜM: Büyük karede [AC] köşegenini çizersek, küçük karenin de köşegeninin üzerinden geçecektir. Köşegenler 90 yi, 45 45 olarak böldüğü için, AKE üçgeni bir 45- 45- 90 üçgeni olur. Dolayısıyla KE 12 cm olur. DKE 2 2 2 2 2 üçgeninde pisagor yaparsak, a 12 4 10 a 144 160 a 16 a 4 cm dir. Cevap : B 9) ABCD kare [AC] [EB] {F} FB 20 cm AE 3 ED Yukarıda verilenlere göre, AC kaç cm dir? A) 16 B) 18 2 C) 24 D) 25 E) 28 2 ÇÖZÜM: 3k k AE 3 ED karenin bir kenarı 4k olur. Köşegenler, aynı zamanda açıortaydı. [AF] açıortayına göre, EF 3 k 20 5 4 k 7 EF 15 cm dir. EB 35 cm olur. EAB üçgeni bir 3k – 4k – 5k üçgeni olduğundan, 5k 35 k 7 cm dir. AB 4k 28 cm olur. Köşegenin uzunluğu ise, AC 28 2 cm olur. Cevap : E www.matematikkolay.net 10) ABCD kare m(DCE) m(ECF) AE 6 cm DC 15 cm Yukarıda verilenlere göre, AF x kaç cm dir ? A) 4 B) 6 C) 7 D) 8 E) 9 ÇÖZÜM: DE 15 6 9 cm olur. [CE] ve [BA] yı şekildeki gibi uzatalım. DEC üçgeni ile AEG üçgeni arasında kelebek benzer – liği vardır. AG 15 5 6 2 9 3 2 2 2 2 AG 10 cm dir. m(AGE) m(DCE) dir (iç ters açı). GFC üçgeni ikizkenar üçgen olur. FC 10 x tir. FB 15 x tir. BFC üçgeninde pisagor yaparsak, 15 (15 x) (10 x) 225 225 30x x 2 100 20x x 450 100 20x 30x 350 50x x 7 cm buluruz. Cevap : C
