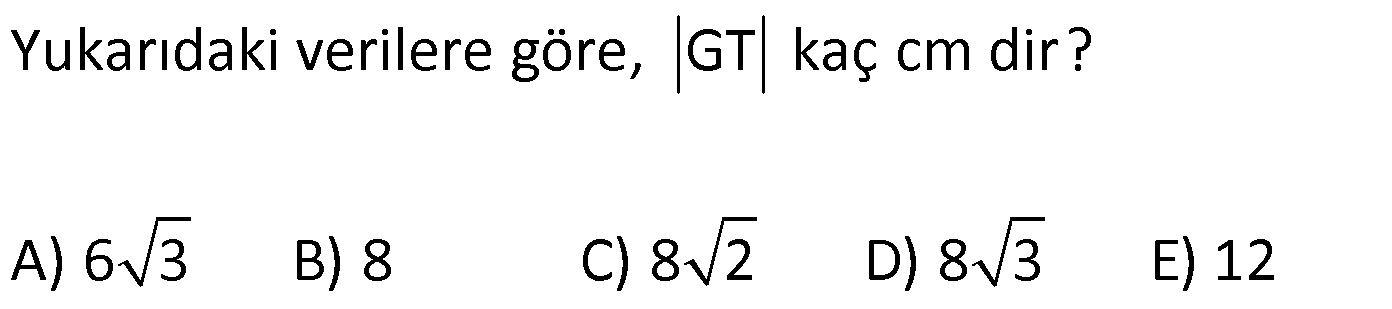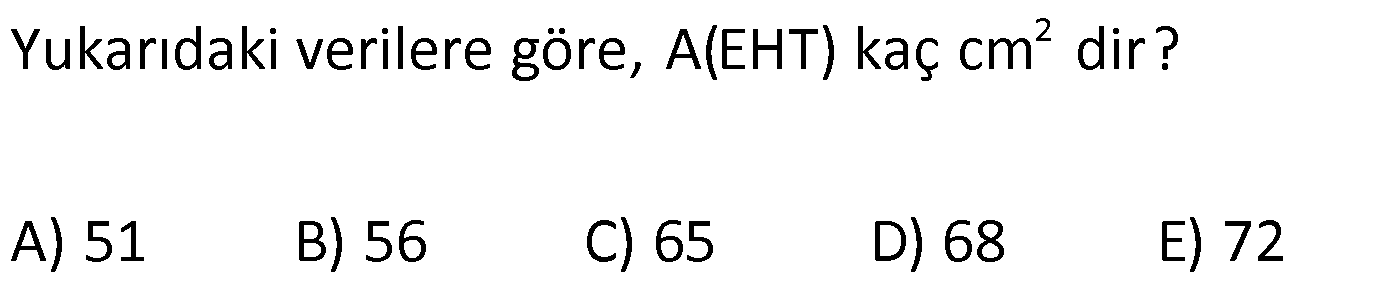Bu bölümde Kare Dik Prizma ile ilgili 8 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
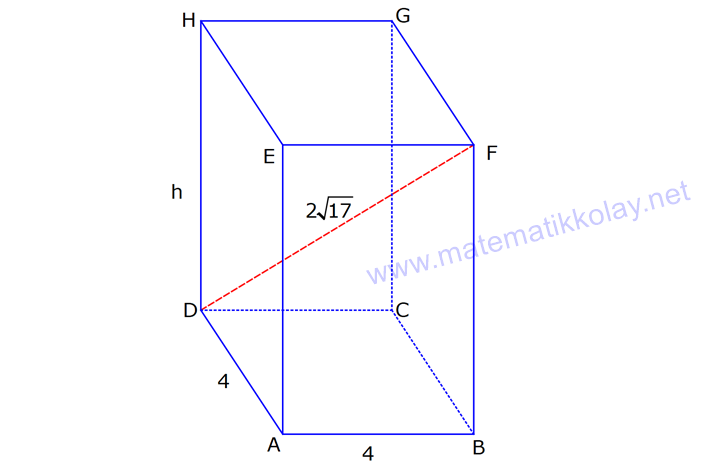
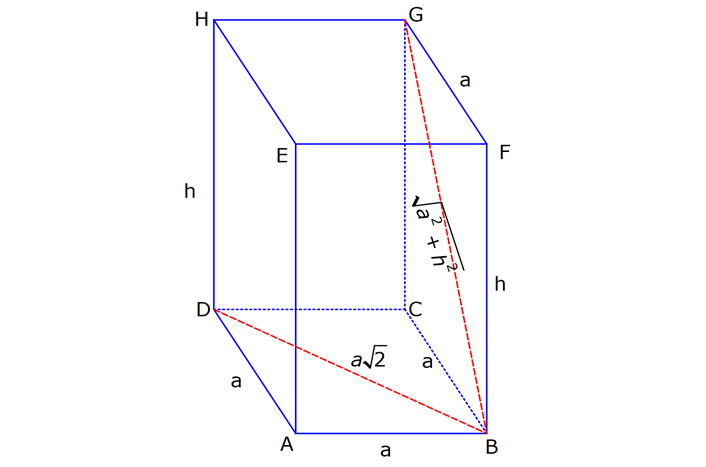
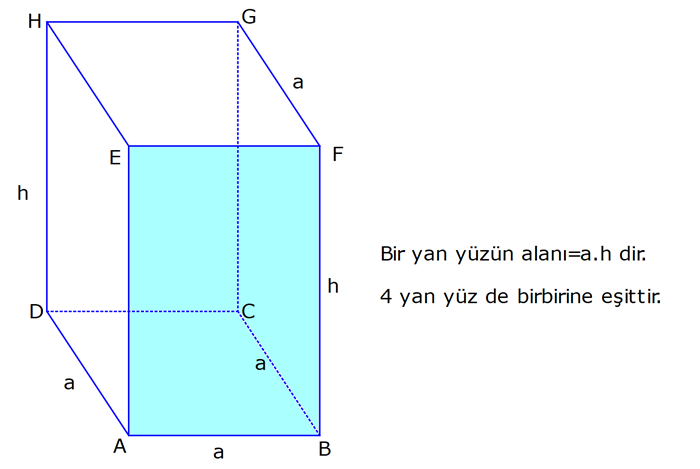
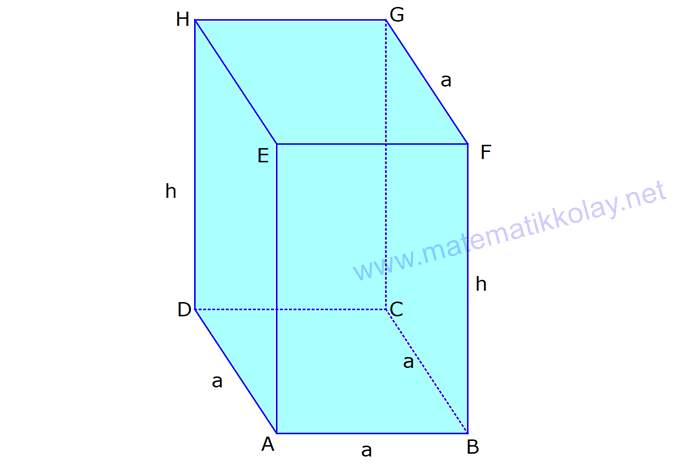
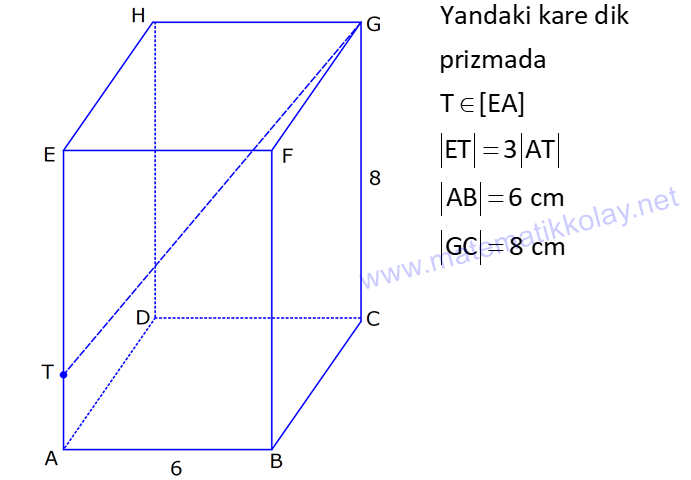
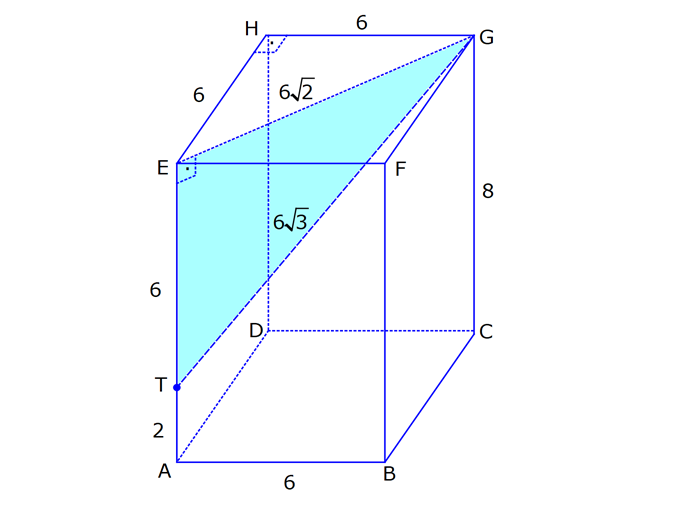
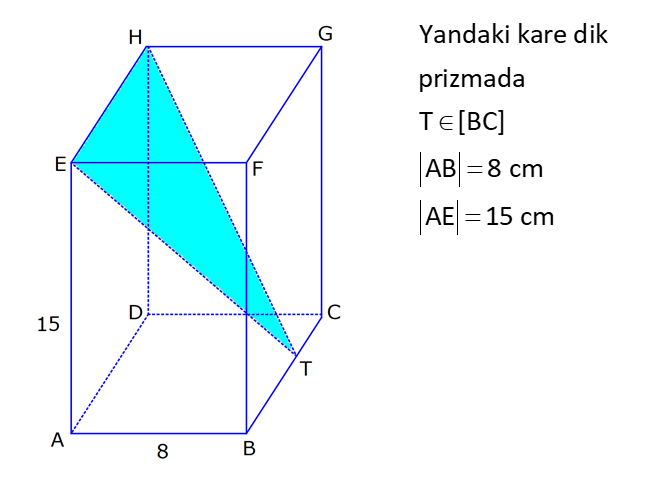
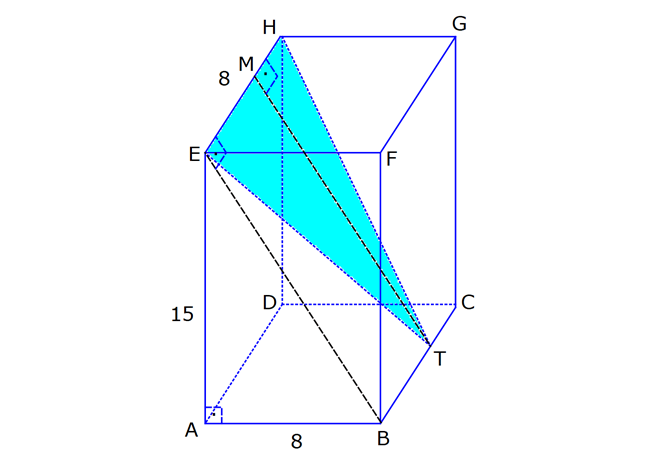
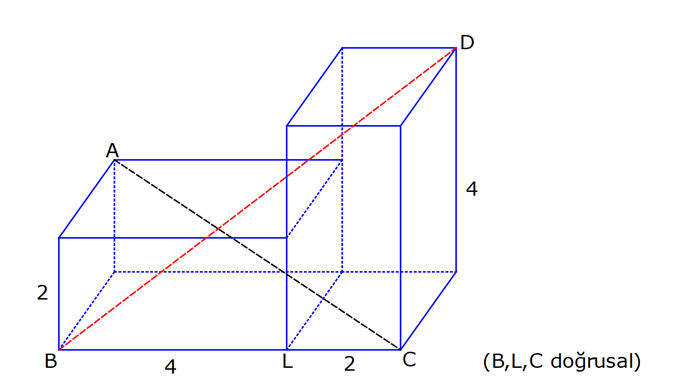
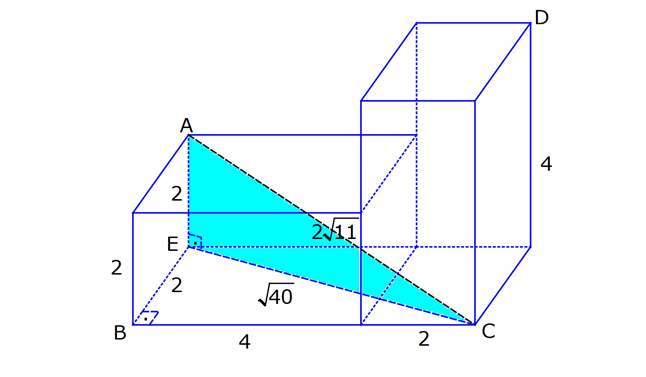
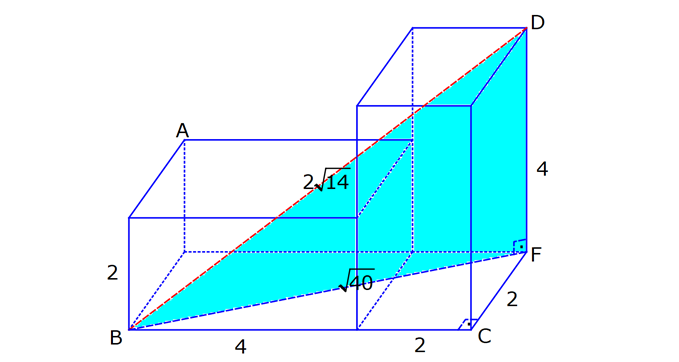
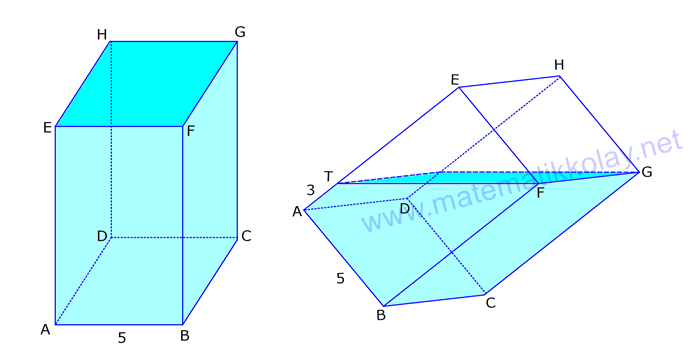
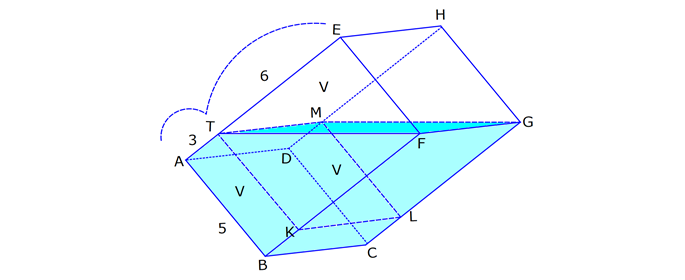
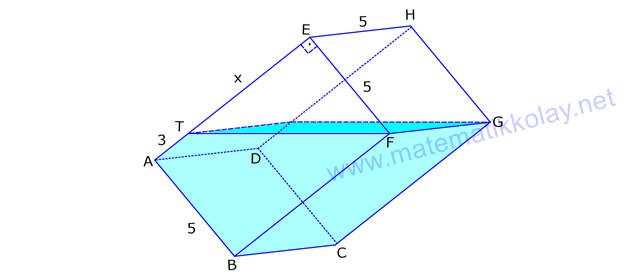
KARE DİK PRİZMA www.matematikkolay.net 1) 3 Taban ayrıtı 4 cm olan bir kare dik prizmanın cisim köşegeni 2 17 cm olduğuna göre, hacmi kaç cm tür? A) 80 B) 90 C) 96 D) 102 E) 120 ÇÖZÜM: 2 2 2 2 2 2 Tabanı kare olan dik prizmaya, kare dik prizma denir. Buna göre, taban ayrıtları eşittir. Cisim köşegeni için 4 4 h 2 17 eşitliğini kurabiliriz. 32 h 68 32 h 68 h 36 h 6 cm dir. Not : 2 2 3 Taban ayrıtı a, yüksekliği h olan bir kare dik prizmanın hacmi a .h dir. O halde, Hacim 4 .6 16.6 96 cm tür. Cevap: C Not : 2) 3 Farklı yüzey köşegenlerinin uzunlukları 3 2, 4 2 cm olan bir kare dik prizmanın hacmi en fazla kaç cm tür? A) 8 17 B) 9 23 C) 16 2 D) 24 3 E) 36 2 ÇÖZÜM: 2 2 2 2 2 2 Kare dik prizmanın bir taban ayrıtı a, yüksekliği h olsun. Taban ait köşegen a a a 2 dir. Tabana ait köşegen 3 2 cm ise, a 3 cm dir. 3 h 4 2 9 h 32 h 23 h 23 cm dir. Hacim I. durum: 2 2 3 2 2 2 2 2 2 3 3 a h 3 . 23 9 23 cm olur. Tabana ait köşegen 4 2 cm ise, a 4 cm dir. 4 h 3 2 16 h 18 h 2 h 2 cm dir. Hacim a h 4 . 2 16 2 cm olur. En fazla hacim 9 23 cm oluyor. Cevap : B 9 23 81.23 1863 16 2 II. durum: 256.2 512 3) 2 3 2 Taban alanı 72 cm ve hacmi 144 cm olan bir kare dik prizmanın yanal alanı kaç cm dir? A) 32 2 B) 36 2 C) 40 2 D) 48 2 E) 60 2 www.matematikkolay.net ÇÖZÜM: 2 3 2 a 72 a 72 6 2 cm dir. Hacmi 144 cm ise 72.h 144 h 2 cm dir. Kare dik prizmanın yanal alanı 4.a.h dir. Yanal alan 4.6 2.2 48 2 cm dir. Cevap: D Not : 4) 2 3 Ayrıtları cm cinsinden 1 den büyük bir tamsayı olan bir kare dik prizmanın yüzey alanı 290 cm olduğuna göre, hacmi kaç cm tür? A) 240 B) 250 C) 260 D) 275 E) 300 ÇÖZÜM: 2 Tabanlar Yanal Alan 2 May.29 Kare dik prizmanın yüzey alanı 2a 4.a.h dir. Buna göre, 2a 4ah 290 2a(a 2h) 290 a(a 2h) 145 1’den büyük tam sayı oldukları için a 5 , Not : 5 2 3 a 2h 29 olmak zorundadır. a 2h 29 2h 24 h 12 cm dir. O halde, hacim 5 .12 25.12 300 cm tür. Cevap :E 5) Yandaki kare dik prizmada T [EA] ET 3 AT AB 6 cm GC 8 cm Yukarıdaki verilere göre, GT kaç cm dir? A) 6 3 B) 8 C) 8 2 D) 8 3 E) 12 ÇÖZÜM: www.matematikkolay.net 2 2 EA 8 cm dir. ET 3 AT olduğu için bu uzunluğu 6 ve 2 cm olarak paylaşırlar. [EG] yi çizelim. EG 6 2 cm dir. TEG üçgeninde de pisagor yaparsak, TG 6 6 2 36 72 108 6 3 cm dir. Cevap: A 6) Yandaki kare dik prizmada T [BC] AB 8 cm AE 15 cm 2 Yukarıdaki verilere göre, A(EHT) kaç cm dir? A) 51 B) 56 C) 65 D) 68 E) 72 ÇÖZÜM: Taban kare olduğu için EH 8 cm dir. Üçgenin yüksekliği ise, EB ile aynıdır. ABE üçgeni 8 -15-17 üçgeni olduğu için EB 17 cm dir. 8 A(EHT) 4 .17 2 2 68 cm dir. Cevap : D 7) Taban ayrıtı 2 cm, yüksekliği 4 cm olan iki tane kare dik prizma yukarıdaki gibi yanyana konuyor. Buna AC göre, oranı kaçtır? BD 2 2 7 11 13 5 A) B) C) D) E) 15 13 14 3 2 4 ÇÖZÜM: www.matematikkolay.net 2 2 2 İlk önce AC yi bulalım. [EC] yi çizelim. BEC üçgeninde pisagor yaparsak, EC 2 6 40 cm dir. AEC üçgeninde pisagor yaparsak, AC 2 40 44 4.11 2 11 cm buluruz. 2 2 2 Şimdi BD yi bulalım. [BF] yi çizelim. BCF üçgeninde pisagor yaparsak, BF 2 6 40 cm dir. BFD üçgeninde pisagor yaparsak, BD 4 40 56 4.14 2 14 cm buluruz. O halde, AC 2 BD 11 2 11 buluruz. Cevap : C 14 14 8) Taban ayrıt uzunluğu 5 cm olan kare dik prizma şek – lindeki kabın içi başlangıçta su ile doludur. 1 Daha sonra şekildeki gibi eğilerek, içindeki suyun ü 3 dökülüyor. AT 3 cm olduğuna göre, başlangıçta k 3 apta kaç cm su vardı? A) 200 B) 225 C) 250 D) 300 E) 325 ÇÖZÜM: Yukarıdaki gibi, prizmanın tabanına paralel T noktasından yeni bir taban oluşturalım (TKLM tabanı). TKLM tabanlı kare dik prizmanın yarısı dökülmüştür. Dökülen hacme V dersek, bu prizmanın hacmi 2V olur. 1 Tüm hacim ise 3V dir ü dökülmüştü. 3 O halde, alt kısımdaki kare dik prizmanın hacmi de V dir. Tabanları aynı olan bu prizmaların hacimleri oranı, yükseklikleri oranına eşittir. 3 V TE 2 V 2 3 TE 6 cm dir. Buna göre, Başlangıçtaki suyun hacmi 5 .9 225 cm tür. Cevap :B II.Yol: www.matematikkolay.net 3 2 Dökülen kısım dik üçgen tabanlı bir dik prizmadır. 5.x 25x Bunun hacmi 5 cm tür. 2 2 Tüm prizmanın hacmi 5 (3 x) tir. 25 2 x 2 5 2 3 6 1 olduğuna göre, (3 x) 3 x 1 3x 6 2x x 6 cm dir. O halde, 2(3 x) 3 suyun tamamı 5 (3 x) 25.9 225 cm tür.
