Bu bölümde Dörtgenlerde Alan ile ilgili 7 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
1.SORU
 |  |  |  |  |
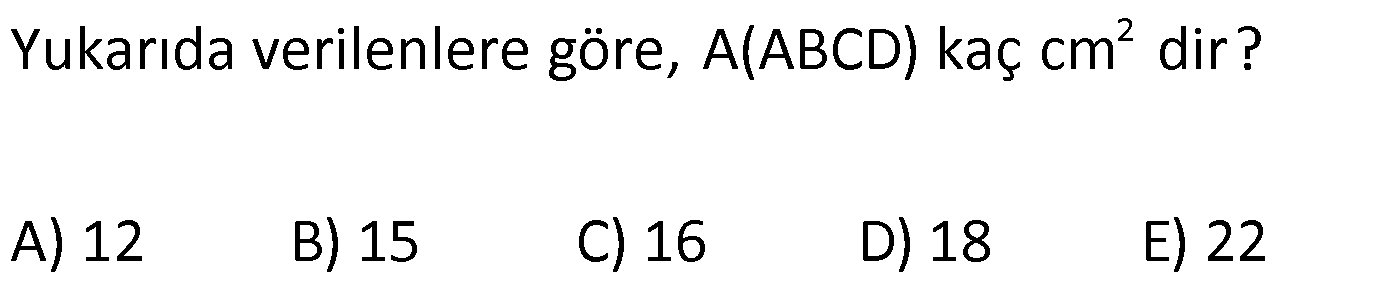
Çözüm için Tıklayınız.
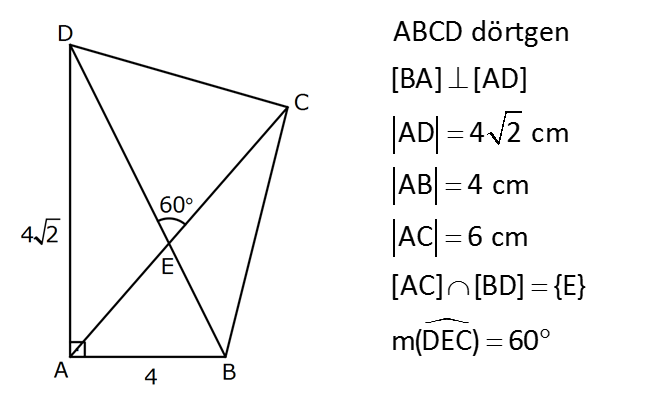
2.SORU
| | | | | |
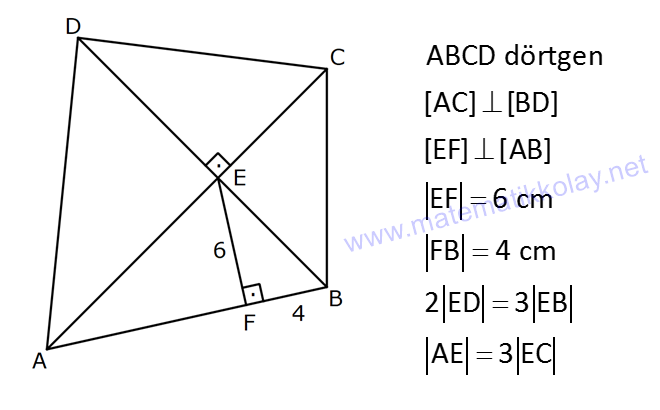
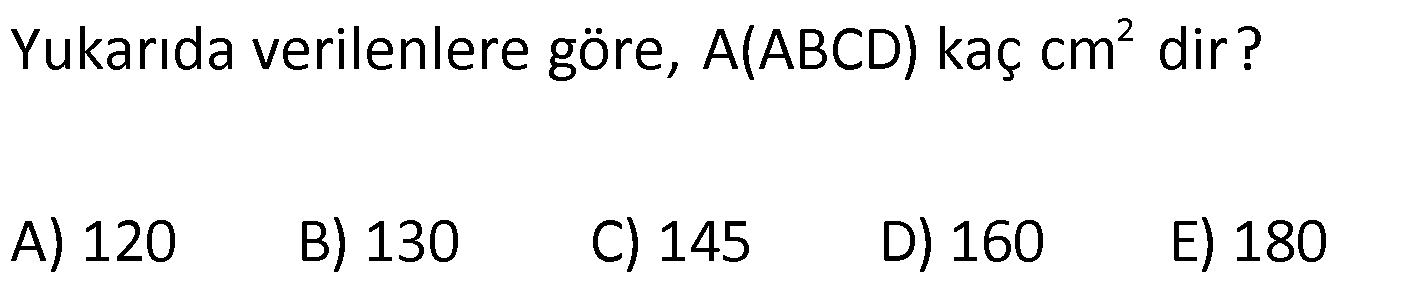
Çözüm için Tıklayınız.
3.SORU
| | | | | |
Çözüm için Tıklayınız.
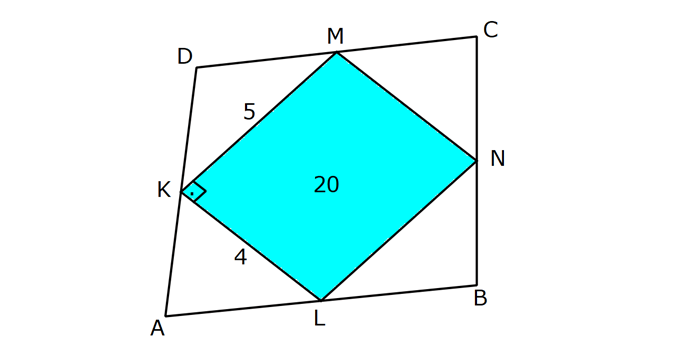
4.SORU
| | | | | |
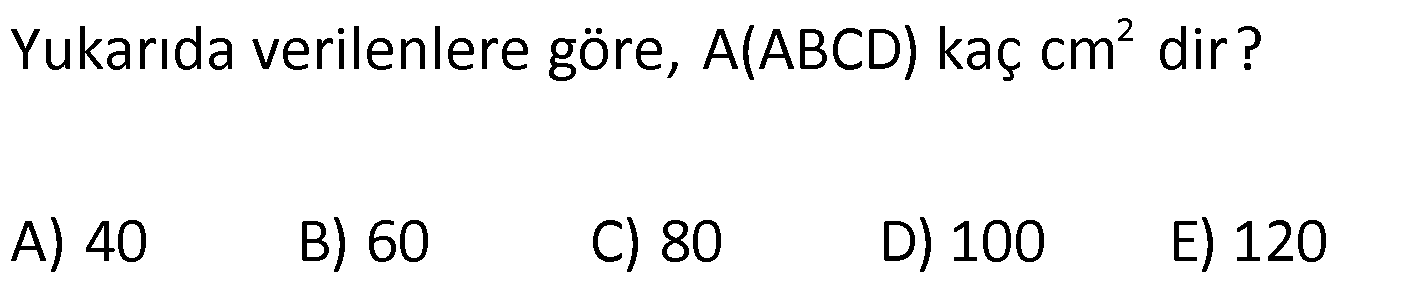
Çözüm için Tıklayınız.
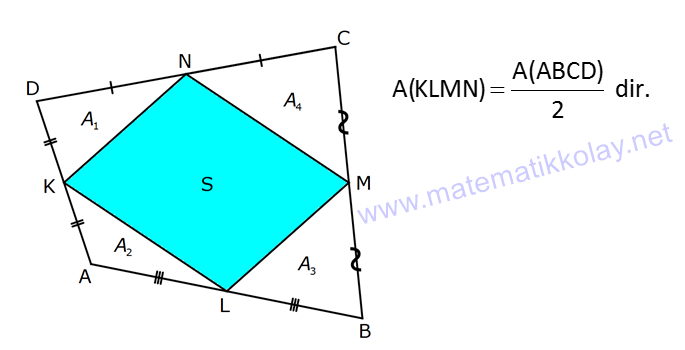
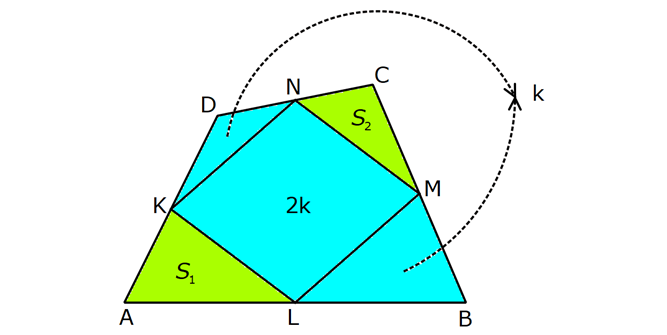
5.SORU
| | | | | |
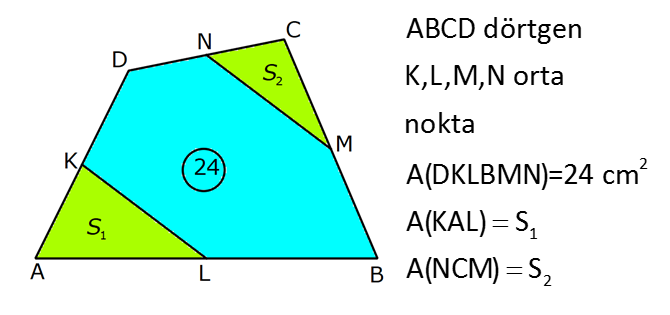
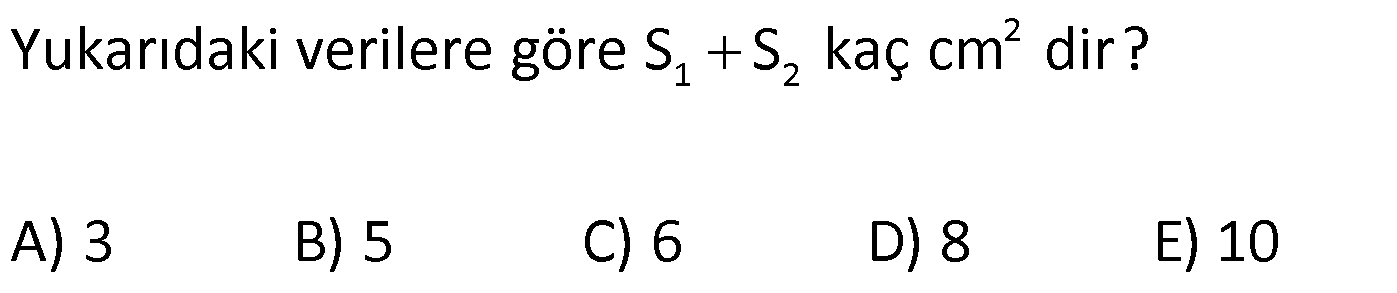
Çözüm için Tıklayınız.
6.SORU
| | | | | |
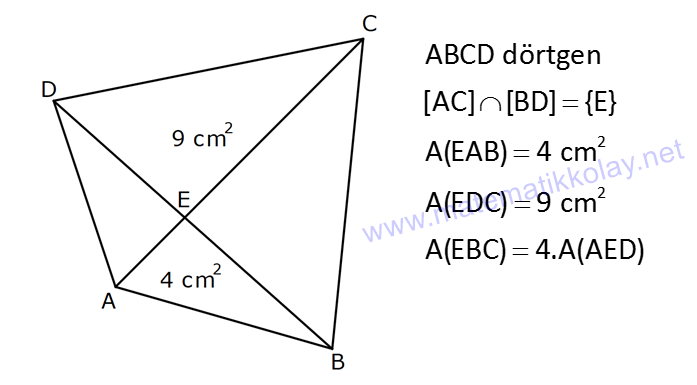
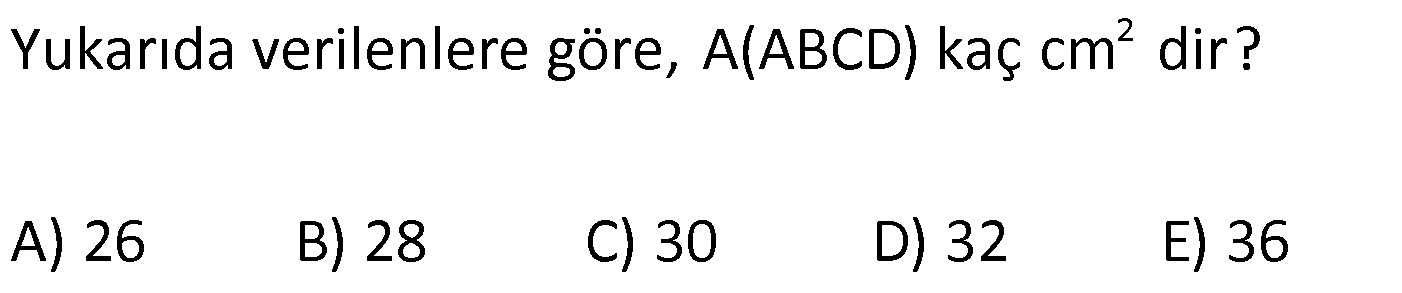
Çözüm için Tıklayınız.
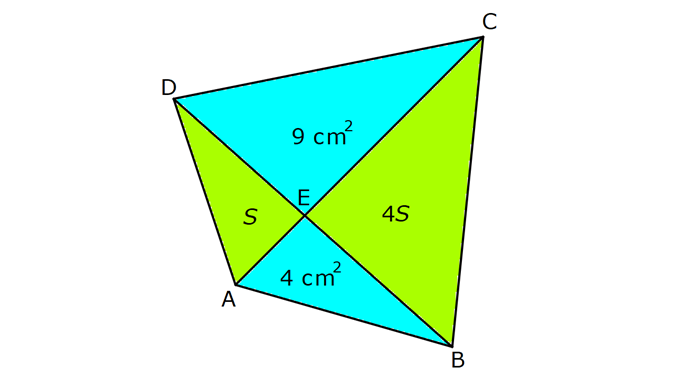
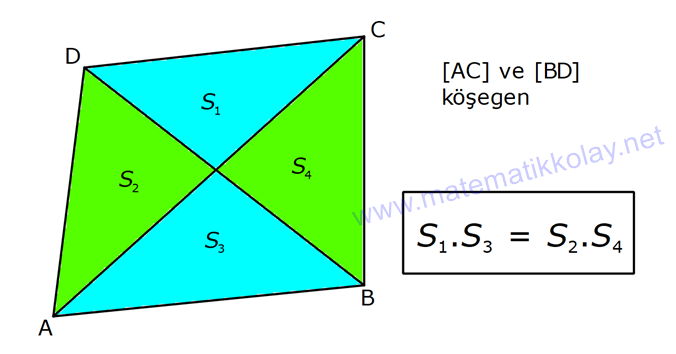
7.SORU
| | | | | |
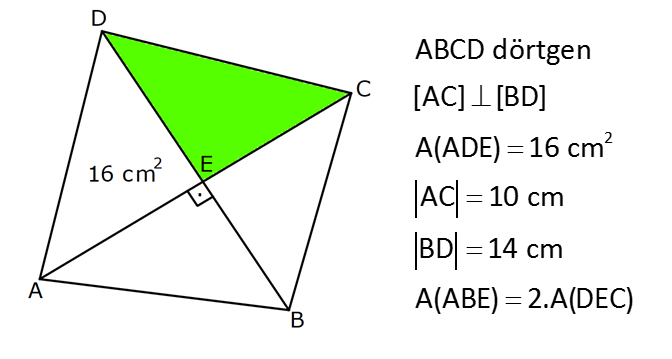
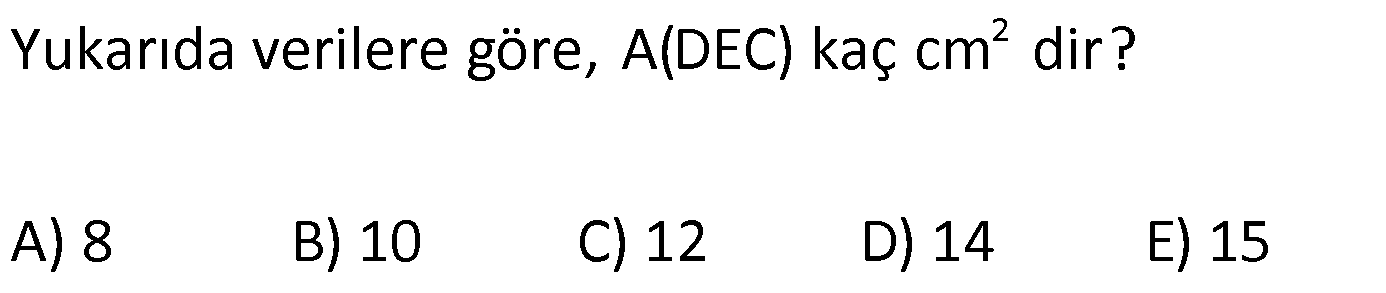
Çözüm için Tıklayınız.
Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
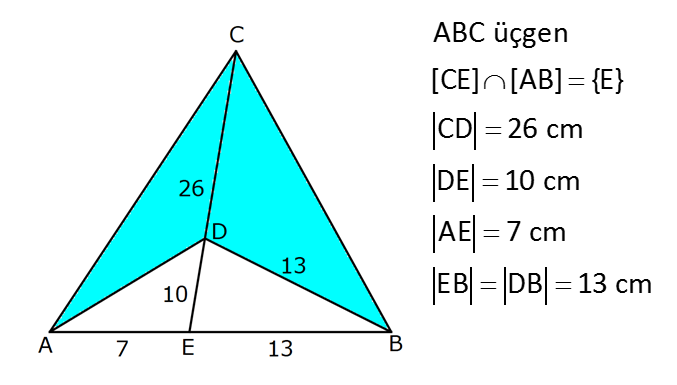
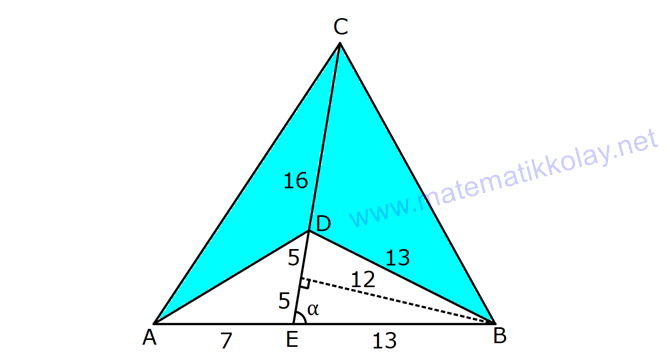
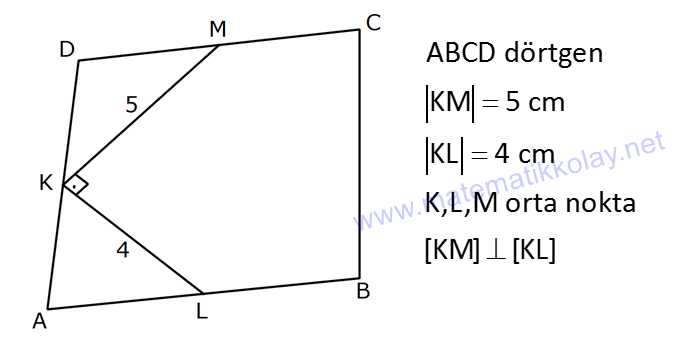
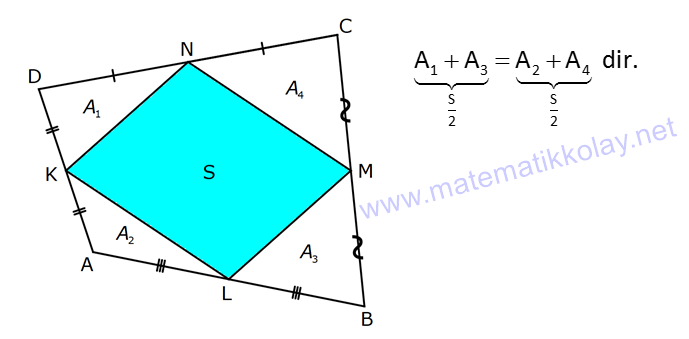
DÖRTGENDE ALAN www.matematikkolay.net 1) ABCD dörtgen [BA] [AD] AD 4 2 cm AB 4 cm AC 6 cm [AC] [BD] {E} m(DEC) 60 2 Yukarıda verilenlere göre, A(ABCD) kaç cm dir? A) 12 B) 15 C) 16 D) 18 E) 22 ÇÖZÜM: 2 2 2 2 2 DB 4 (4 2) DB 16 32 DB 48 DB 4 3 cm dir. Bir dörtgenin köşegen uzunlukları e ve f olsun. Arasındaki açı da ise, bu dörtgenin 1 alanı e f sin dır. 2 Buna göre, 1 A(ABCD) 4 3 6 sin60 Not : s 2 Not : 3 in60 2 1 A(ABCD) 2 4 2 3 6 3 3 2 2 A(ABCD) 18 cm dir. Cevap: D 2) ABCD dörtgen [AC] [BD] [EF] [AB] EF 6 cm FB 4 cm 2 ED 3 EB AE 3 EC 2 Yukarıda verilenlere göre, A(ABCD) kaç cm dir? A) 120 B) 130 C) 145 D) 160 E) 180 ÇÖZÜM: 2 2 2 2 2 2 13 2 2 2 2 2 2 EB 4 6 EB 16 36 EB 52 EB 52 4.13 2 13 cm dir. 2 ED 3 EB ED 3 13 cm dir. AEB üçgeninde öklit teoreminden, AF .4 6 AF 9 cm dir. Pisagor teoreminden, AE 6 9 AE 36 81 AE 1 BD = 2 13 + 3 13 = 5 13 cm dir. 3 13 13 17 AE 117 9.13 3 13 cm dir. AE 3 EC Bir dörtgenin köşegen uzunlukları e ve f olsun. Bu köşegenler dik kesişiyorsa 1 Alan e f dir. 2 Buna göre, 1 A(ABCD) 2 AC = 3 13 + 13 = 4 13 cm dir. Not : 5 13 4 2 2 13 10.13 130 cm dir. Cevap : B www.matematikkolay.net 3) ABC üçgen [CE] [AB] {E} CD 26 cm DE 10 cm AE 7 cm EB DB 13 cm 2 Yukarıda verilenlere göre, A(ABCD) kaç cm dir? A) 120 B) 140 C) 180 D) 200 E) 240 ÇÖZÜM: ABCD iç bükey (konkav) dörtgeninde köşegenler CD 26 cm ve AB 20 cm dir. Aradaki açının sinüsüne ihtiyacımız var. Bunun için EDB ikizkenar üçgenini kullanabiliriz. Şekildeki gibi B den bir dikme indirelim. 5 12 13 üçgeni oluşur. 12 sin tür. O halde, 13 1 A(ABCD) 2 26 13 12 20 13 2 240 cm buluruz. Cevap : E 4) ABCD dörtgen KM 5 cm KL 4 cm K,L,M orta nokta [KM] [KL] 2 Yukarıda verilenlere göre, A(ABCD) kaç cm dir? A) 40 B) 60 C) 80 D) 100 E) 120 ÇÖZÜM: 2 N, [BC] nin orta noktası olsun. Dörtgenin orta noktalarının birleşimiyle paralelkenar oluşuyordu. m(MKL) 90 olduğundan KLMN ayrıca bir dikdörtgen olur. A(KLMN) 5.4 20 cm dir. Kural gereği bu KLMN dörtg 2 eninin alanı, ABCD dörtge – ninin alanının yarısıdır. Bu sebeple, A(ABCD) 2.20 40 cm dir. Cevap : A Not : A(ABCD) A(KLMN) dir. 2 5) www.matematikkolay.net 2 1 2 ABCD dörtgen K,L,M,N orta nokta A(DKLBMN)=24 cm A(KAL) S A(NCM) S 2 1 2 Yukarıdaki verilere göre S S kaç cm dir? A) 3 B) 5 C) 6 D) 8 E) 10 ÇÖZÜM: 1 2 1 2 Or ta noktaların birleşimiyle oluşan KLMN dörtge – ninin alanına 2k diyelim. Kural gereği karşılıklı üçgenlerin alanları toplamı birbirine eşit ve k dır. 3k 24 olur. k 8 dir. S S k olduğundan S S 8 c 2 m buluruz. Cevap : D Not : 1 3 2 4 S S 2 2 A A A A dir. 6) 2 2 ABCD dörtgen [AC] [BD] {E} A(EAB) 4 cm A(EDC) 9 cm A(EBC) 4.A(AED) 2 Yukarıda verilenlere göre, A(ABCD) kaç cm dir? A) 26 B) 28 C) 30 D) 32 E) 36 ÇÖZÜM: A(AED) S diyelim. A(EBC) 4S olur. Kural gereği karşılıklı alanların çarpımı birbirine eşittir. S. 4 S 4 2 2 2 2 .9 S 9 S 3 cm dir. 4S 4.3 12 cm olur. O halde, A(ABCD) 3 12 4 9 28 cm dir. Cevap : B Not : www.matematikkolay.net 7) 2 ABCD dörtgen [AC] [BD] A(ADE) 16 cm AC 10 cm BD 14 cm A(ABE) 2.A(DEC) 2 Yukarıda verilere göre, A(DEC) kaç cm dir ? A) 8 B) 10 C) 12 D) 14 E) 15 ÇÖZÜM: 10. 14 A(ABCD) 7 2 2 70 cm dir. A(DEC) S olsun, A(ABE) 2S olur. S.2S 16.A(BEC) 2 2 S 16 8 2 2 2 2 2 2 2 36 12 .A(BEC) S A(BEC) 8 Üçgenlerin alanları toplamı 70 cm yi vermelidir. S 16 S 2S 70 8 S 3S 54 8 24S S 54 8 S 24S 432 S 24S 432 0 (S 36)(S 12) 0 S 12 dir. Cevap : C
