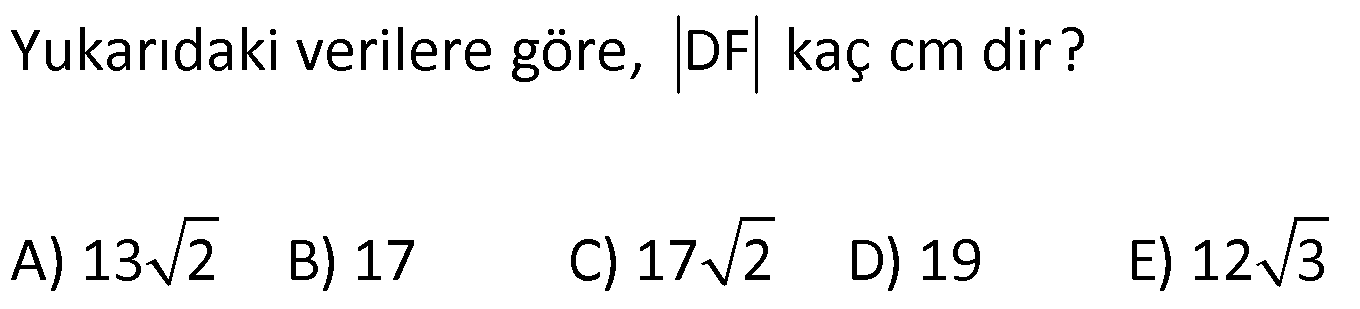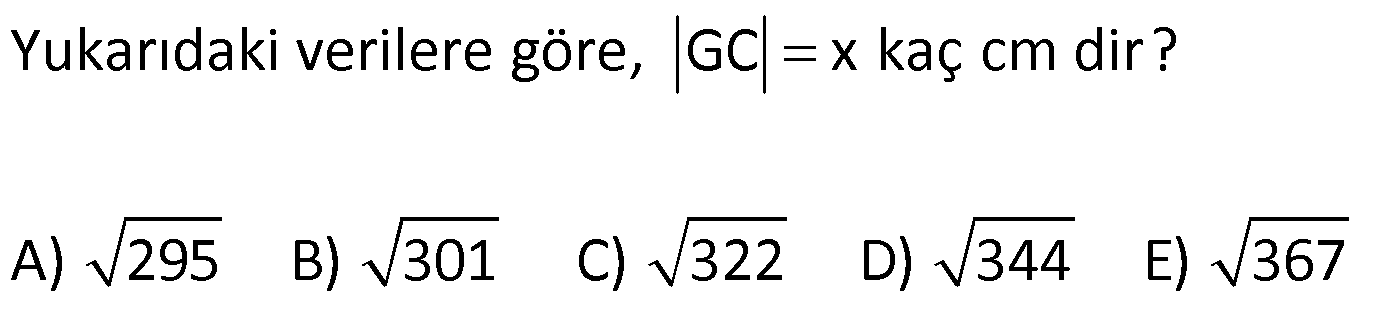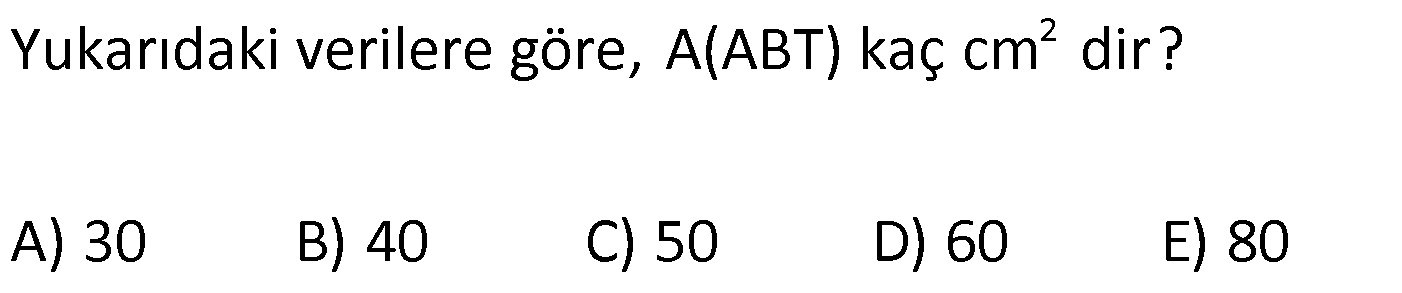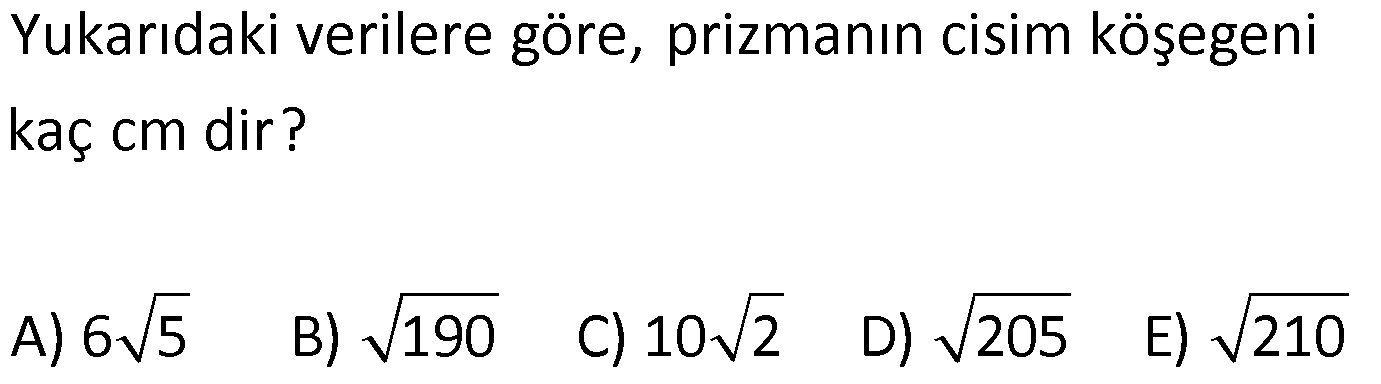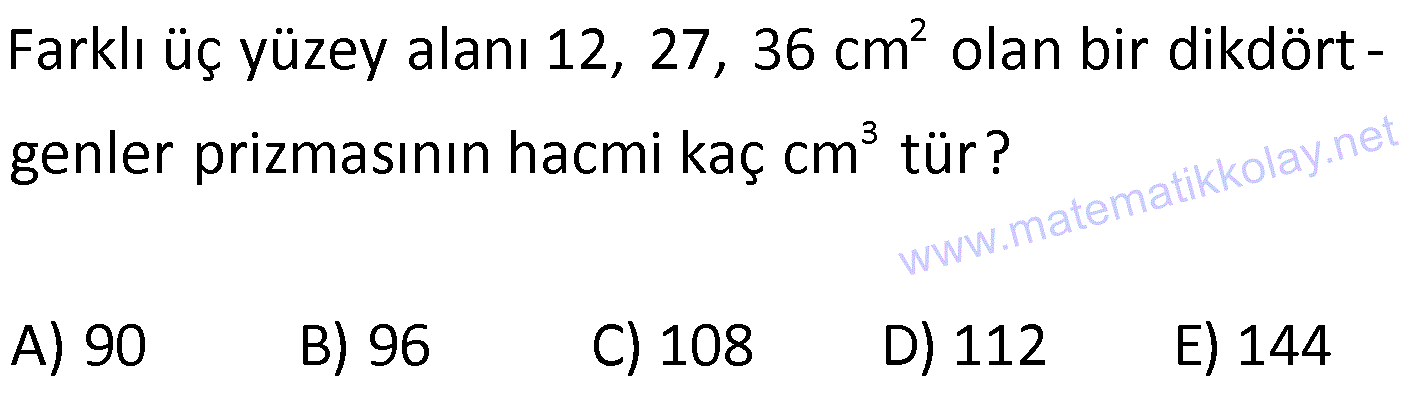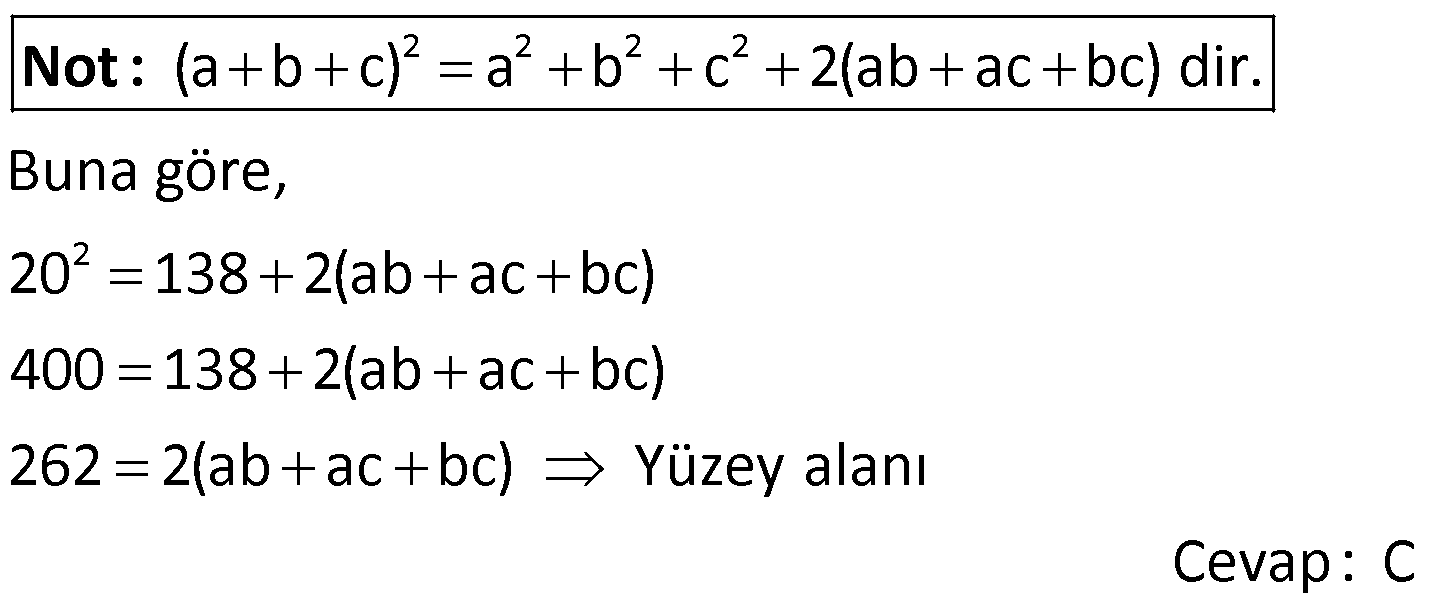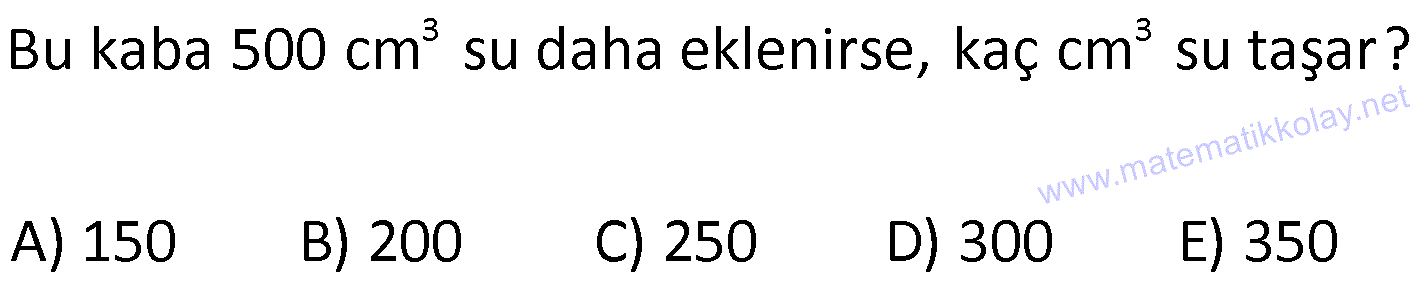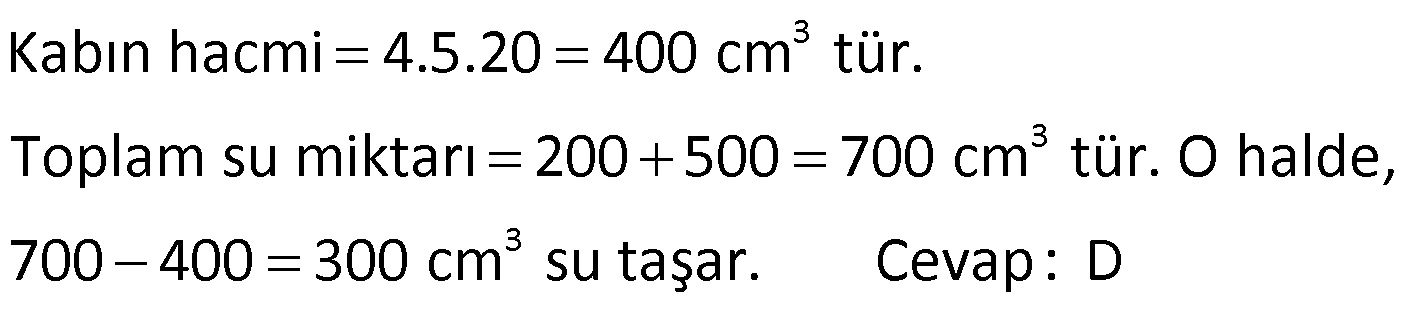Bu bölümde Dikdörtgenler Prizması ile ilgili 14 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
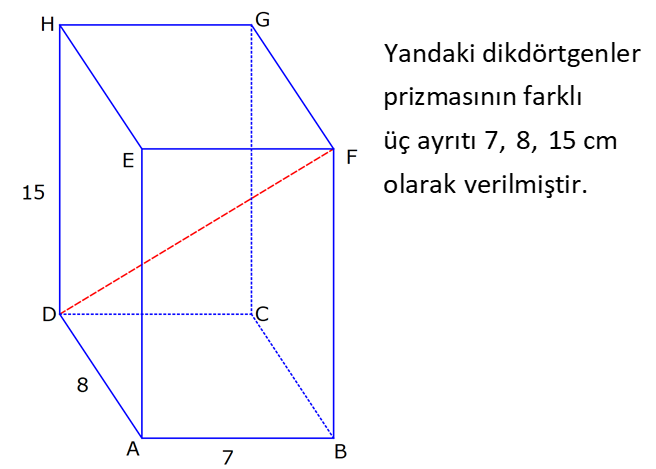
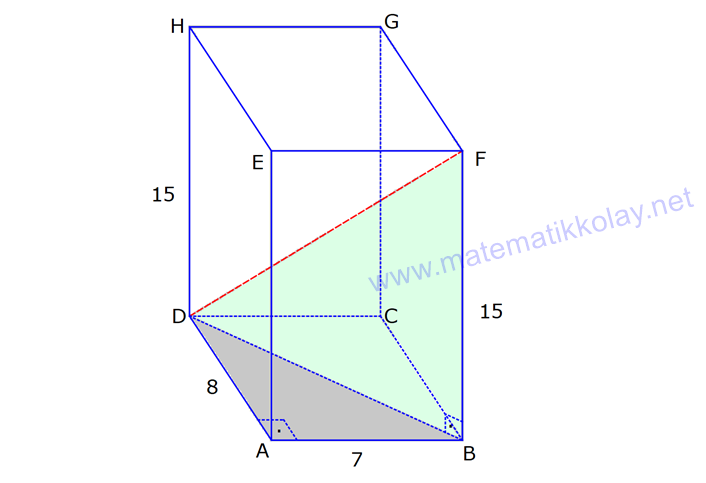
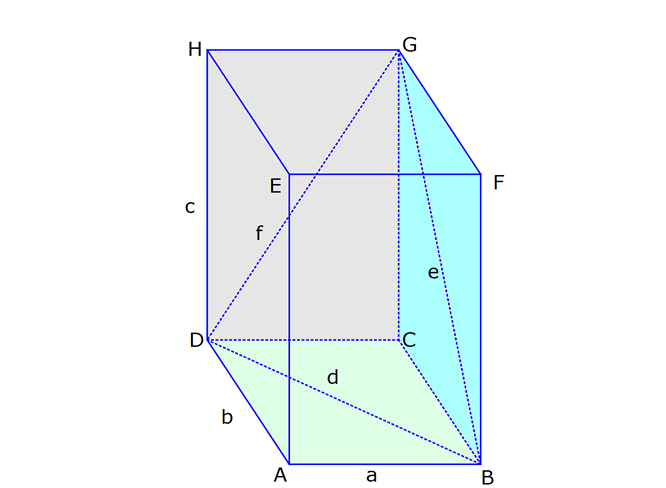
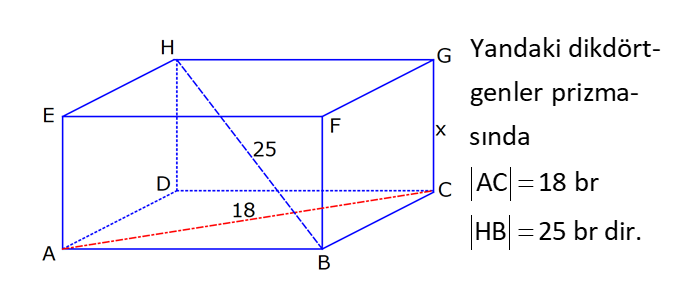
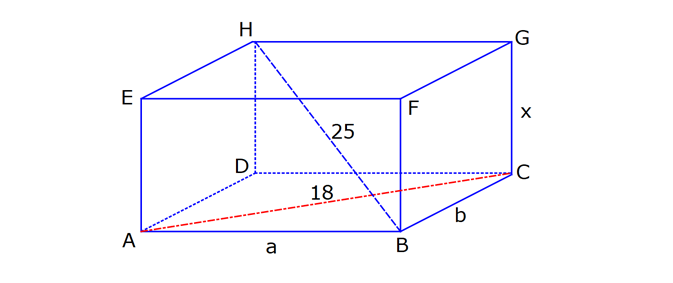
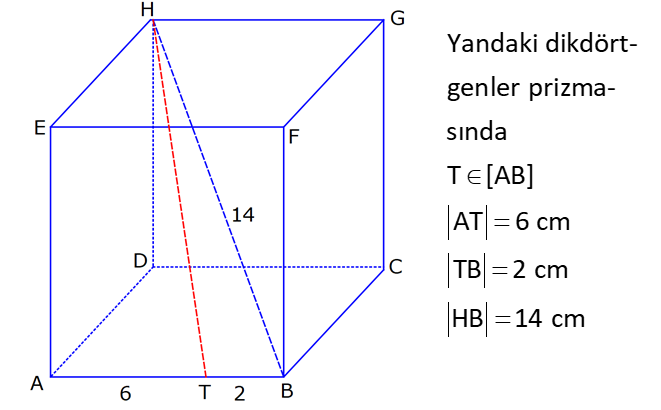
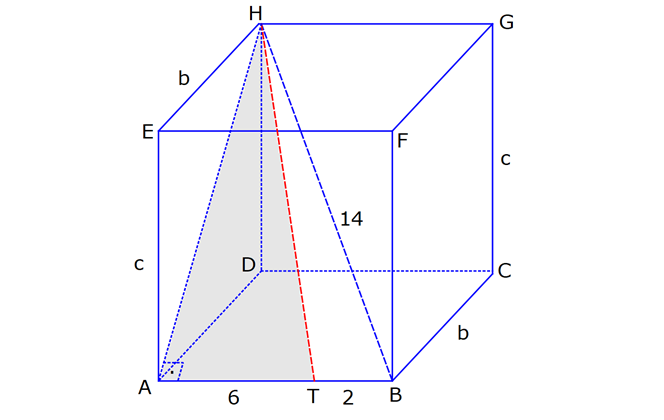
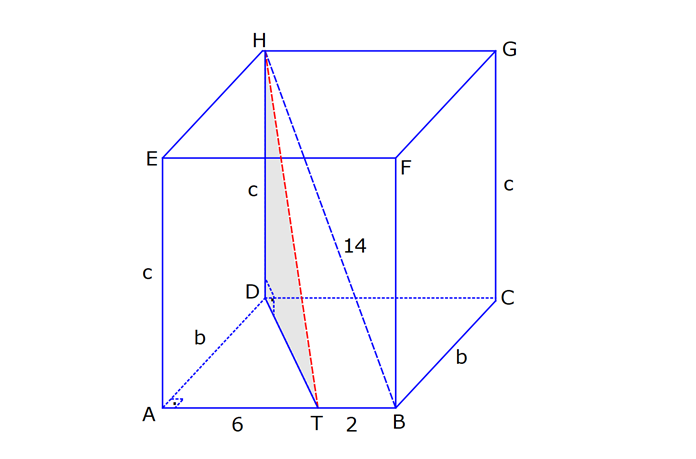
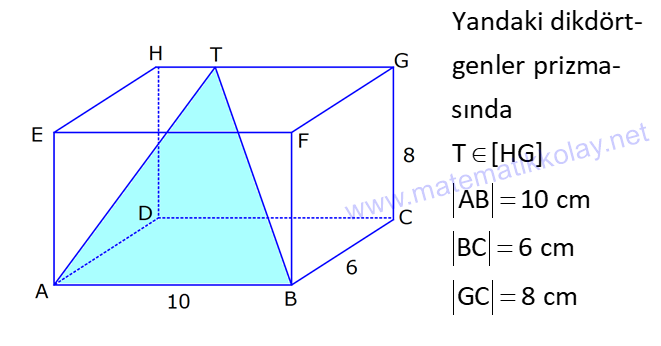
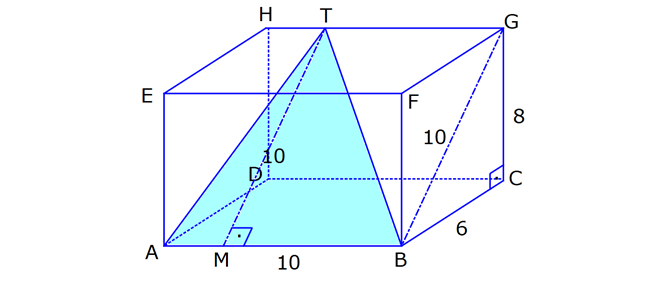
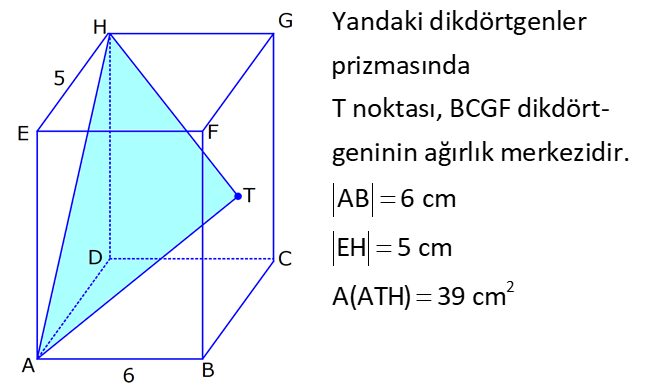
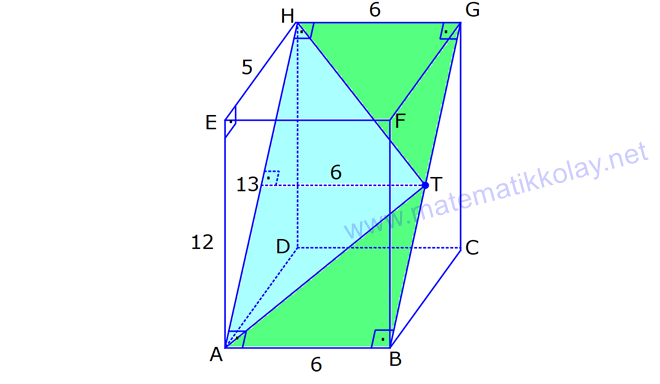
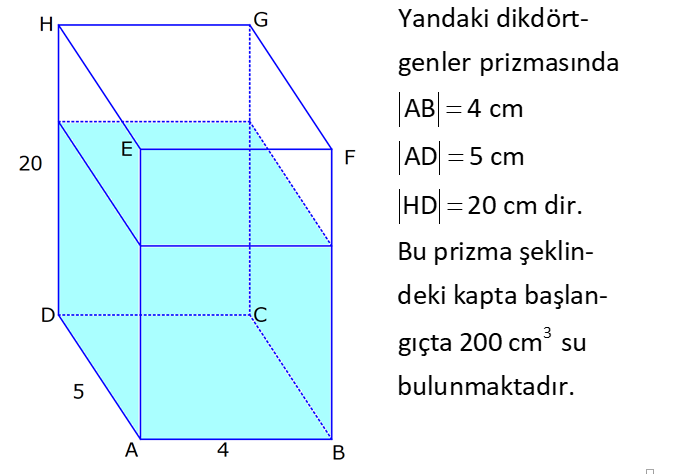
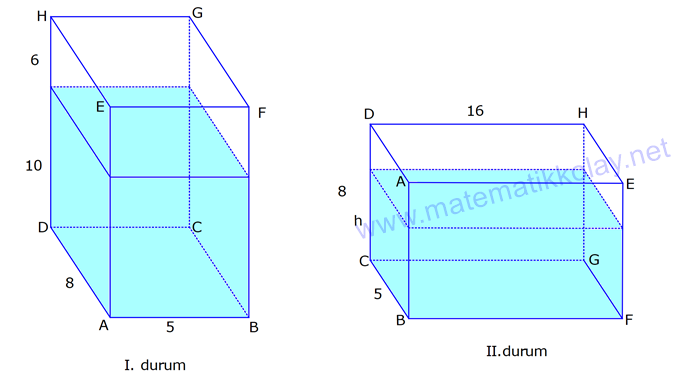
DİKDÖRTGENLER PRİZMASI www.matematikkolay.net 1) Yandaki dikdörtgenler prizmasının farklı üç ayrıtı 7, 8, 15 cm olarak verilmiştir. Yukarıdaki verilere göre, DF kaç cm dir? A) 13 2 B) 17 C) 17 2 D) 19 E) 12 3 ÇÖZÜM: 2 2 2 2 2 Dikdörgenler prizmasının bütün yüzeyleri dikdörtgendir. Bu sebeple pisagor hesabını sıklıkla kullanırız. [DB] doğru parçasını çizelim. DAB üçgeninde pisagor yaparsak, DB 8 7 DB 64 49 DB 113 tür. BDF Not : 2 2 2 2 2 üçgeninde pisagor yaparsak, DF DB 15 DF 113 225 DF 338 DF 338 169.2 13 2 cm dir. Cevap: A Aynı yüzeye ait olmayan köşeleri birleştiren doğru parçasına denir. Bir II.Yol: Not : cisim köşegeni 2 2 2 2 2 2 dikdörtgenler prizmasının farklı ayrıtları a, b ve c olsun. Cisim köşegeni a b c ile bulunur. Buna göre, [DF] cisim köşegenidir. DF 7 8 15 49 64 225 338 13 2 cm dir. 2) Farklı yüzey köşegenlerinin uzunlukları 41, 65 ve 74 cm olan bir dikdörtgenler prizmasının cisim köşegeni kaç cm dir? A) 6 2 B) 4 5 C) 3 10 D) 5 5 E) 4 6 ÇÖZÜM: www.matematikkolay.net 2 2 Aynı yüzeyde karşılıklı köşeleri birleştiren doğru parçasına denir (d, e, f). Pisagor hesabıyla, yüzey köşegenleri bulunabilir. Prizmanın farklı ayrıtları a, b ve c olsun. a b Not : yüzey köşegeni 2 2 2 2 2 2 2 2 2 2 2 2 2 41 a c 65 b c 74 şeklinde eşitlikleri yazabiliriz. 2(a b c ) 180 a b c 90 Cisim köşegeni a b c 90 9.10 3 10 cm dir. Cevap: C 3) Yandaki dikdörtgenler prizmasında AC 18 br HB 25 br dir. Yukarıdaki verilere göre, GC x kaç cm dir? A) 295 B) 301 C) 322 D) 344 E) 367 ÇÖZÜM: 2 2 2 2 2 2 2 2 2 2 324 2 2 [AC], tabana ait bir yüzey köşegenidir. a b 18 324 tür. [HB], cisim köşegenidir. a b x 25 a b x 625 x 625 324 x 301 x 301 cm dir. Cevap : B 4) Yandaki dikdörtgenler prizmasında T [AB] AT 6 cm TB 2 cm HB 14 cm Yukarıdaki verilere göre, HT kaç cm dir? A) 4 10 B) 5 7 C) 3 20 D) 4 13 E) 2 42 ÇÖZÜM: www.matematikkolay.net 2 2 2 2 2 2 2 2 2 2 2 2 2 2 132 Cisim köşegeni 14 cm ise, 8 b c 14 64 b c 196 b c 132 dir. [HA] yi çizelim. AEH üçgeninde pisagor yaparsak, HA b c 132 dir. HAT üçgeninde pisagor yaparsak, HT HA 6 132 36 16 8 HT 168 4.42 2 42 cm dir. Cevap : E Pisagor için II.Yol: 2 2 2 2 2 2 b 36 2 2 132 [DT] yi çizelim. DAT üçgeninde pisagor yaparsak, DT b 36 dır. HDT üçgeninde pisagor yaparsak, HT c DT b c 36 168 HT 168 4.42 2 42 cm dir. 5) Yandaki dikdörtgenler prizmasında T [HG] AB 10 cm BC 6 cm GC 8 cm 2 Yukarıdaki verilere göre, A(ABT) kaç cm dir? A) 30 B) 40 C) 50 D) 60 E) 80 ÇÖZÜM: ABT üçgeninde [AB] kenarına ait yüksekliği bulalım. Bu yüksekliğin TM uzunluğu ile BG uzunluğu birbirine eşittir. BCG üçgeni 6 – 8 -10 üçgeni olduğundan BG 10 cm dir. TM 10 cm olur. 10.10 100 A(ABT) 50 c 2 2 2 m dir. Cevap: C www.matematikkolay.net 6) 2 Yandaki dikdörtgenler prizmasında T noktası, BCGF dikdörtgeninin ağırlık merkezidir. AB 6 cm EH 5 cm A(ATH) 39 cm Yukarıdaki verilere göre, prizmanın cisim köşegeni kaç cm dir? A) 6 5 B) 190 C) 10 2 D) 205 E) 210 ÇÖZÜM: T noktası ağırlık merkezi ise, bulunduğu dikdörtge – nin köşegenlerinin üzerindedir. Bu sebeple [BG] yüzey köşegeni, T noktasından geçer. ABGH dörtgeni de bir dikdörtgendir ve ATH üçgeni bu dikdörtgenin iç 2 39 2 6 cm 2 2 2 indedir. A(ABGH) 2.A(ATH) 78 cm dir. Buna göre, AB . AH 78 cm olmalıdır. AH 13 cm dir. Buna göre, AEH üçgeni bir 5-12 -13 üçgenidir ve AE 12 cm olur. Cisim köşegeni ise 5 12 6 25 144 36 205 cm d ir. Cevap : D 7) 2 3 Farklı üç yüzey alanı 12, 27, 36 cm olan bir dikdört – genler prizmasının hacmi kaç cm tür? A) 90 B) 96 C) 108 D) 112 E) 144 ÇÖZÜM: 2 2 2 2 2 3 2 a.b 12 a.c 27 b.c 36 olsun. Farklı ayrıtları a, b ve c olan bir dikdörtgenler prizmasının hacmi a.b.c dir. Buna göre, eşitlikleri taraf tarafa çarparsak, a .b .c 12.27.36 (a.b.c) 2 .3.3 .2 Not : 2 2 4 6 2 2 2 3 2 3 3 .3 (a.b.c) 2 .3 (a.b.c) 2 .3 a.b.c 2 .3 4.27 108 cm tür. Cevap: C 8) 3 2 Farklı ayrıt uzunlukları 2, 3, 5 ile orantılı olan bir dikdörtgenler prizmasının hacmi 240 cm ise, yüzey alanı kaç cm dir? A) 112 B) 126 C) 160 D) 196 E) 248 ÇÖZÜM: www.matematikkolay.net 3 3 3 Farklı ayrıtları 2k, 3k ve 5k olsun. Hacmi 240 cm ise, 2k.3k.5k 240 30k 240 k 8 k 2 cm dir. Buna göre, farklı ayrıt uzunlukları 4, 6, 10 cm dir. Farklı ayrıtları a, b ve c olan bir dikdörtge Not : 2 nler prizmasının yüzey alanı 2(ab ac bc) dir. O halde, yüzey alanı 2(4.6 4.10 6.10) 2(24 40 60) 2.124 248 cm dir. Ce vap: E 9) 2 2 2 2 2 Farklı ayrıt uzunlukları a, b, c olan bir dikdörtgenler prizması ile ilgili olarak, a b c 20 cm a b c 138 cm dir. Buna göre, prizmanın yüzey alanı kaç cm dir? A) 206 B) 227 C) 262 D) 288 E) 320 ÇÖZÜM: 2 2 2 2 2 (a b c) a b c 2(ab ac bc) dir. Buna göre, 20 138 2(ab ac bc) 400 138 2(ab ac bc) 262 2(ab ac bc) Yüzey alanı Not : Cevap: C 10) 2 Cisim köşegeni 8 2 cm olan bir dikdörtgenler priz – masının yüzey alanı 233 cm dir. Buna göre, prizmanın tüm ayrıtlarının uzunlukları toplamı kaç cm dir? A) 72 B) 76 C) 82 D) 85 E) 90 ÇÖZÜM: 2 2 2 2 2 2 2 2 2 2 2 128 233 2 Cisim köşegeni 8 2 cm ise, a b c 8 2 a b c 128 cm dir. (a b c) a b c 2(ab ac bc) idi. (a b c) 361 a b c 19 cm dir. Bir dikdörtgenler prizmadasında 3 farklı ayrıt vardır ve bunl 19 arın hepsi 4’er tanedir (Toplam 12 ayrıt). Buna göre, ayrıtların uzunlukları toplamı 4(a b c) 76 cm dir. Cevap: B 11) 2 3 Farklı ayrıt uzunlukları a, b, c olan bir dikdörtgenler prizması ile ilgili olarak, 1 1 1 17 tir. a b c 45 Bu prizmanın yüzey alanı 408 cm olduğuna göre, hacmi kaç cm tür? A) 400 B) 440 C) 480 D) 540 E) 570 ÇÖZÜM: (bc) (ac) (ab) yüzey alanının yarısı 1 1 1 17 payda eşitleyelim. a b c 45 bc ac ab 17 408 204 abc 45 2 204 12 17 abc 3 45 abc 12.45 abc 540 cm tür. Cevap : D www.matematikkolay.net 12) 3 2 Farklı ayrıt uzunlukları toplamı 14 cm olan bir dik – dörtgenler prizmasının ayrıtları 2 şer cm artırılırsa hacmi 190 cm artmaktadır. Buna göre, ilk prizmanın yüzey alanı kaç cm dir? A) 126 B) 140 C) 144 D) 150 E) 164 ÇÖZÜM: İlk önce burayı açalım. a b c 14 cm (a 2)(b 2)(c 2) abc 190 verilmiş. (ab 2a 2b 4)(c 2) abc 190 abc 2ab 2ac 4a 2bc 4b 4c 8 abc 190 abc 14 2(ab ac bc) 4(a b c) 8 abc 2 190 2(ab ac bc) 56 8 190 2(ab ac bc) 64 190 2(ab ac bc) 126 cm dir. Cevap : A 13) 3 Yandaki dikdörtgenler prizmasında AB 4 cm AD 5 cm HD 20 cm dir. Bu prizma şeklindeki kapta başlangıçta 200 cm su bulunmaktadır. 3 3 Bu kaba 500 cm su daha eklenirse, kaç cm su taşar? A) 150 B) 200 C) 250 D) 300 E) 350 ÇÖZÜM: 3 3 3 Kabın hacmi 4.5.20 400 cm tür. Toplam su miktarı 200 500 700 cm tür. O halde, 700 400 300 cm su taşar. Cevap : D 14) Farklı ayrıt uzunlukları 5, 8, 16 cm olan dikdörtgenler prizması şeklindeki kabın içinde başlangıçta 10 cm yüksekliğinde su vardır. II. durumdaki gibi yan dev – rildiğinde suyun yüksekliği kaç cm olur? A) 5 B) 5,5 C) 6 D) 6,5 E) 7 ÇÖZÜM: 3 2 Başlangıçtaki suyun hacmi 5.8.10 400 cm tür. II. durumda tabanın alanı 5.16 80 cm dir. 400 Suyun yüksekliği 5 cm olur. Cevap: A 80
