Bu bölümde Dikdörtgende Açı ve Uzunluk ile ilgili 20 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
1.SORU
 |  |  |  |  |
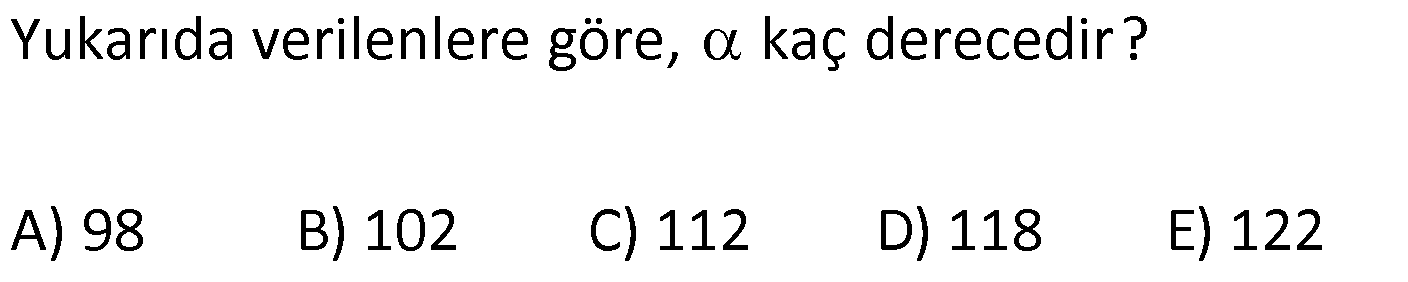
Çözüm için Tıklayınız.
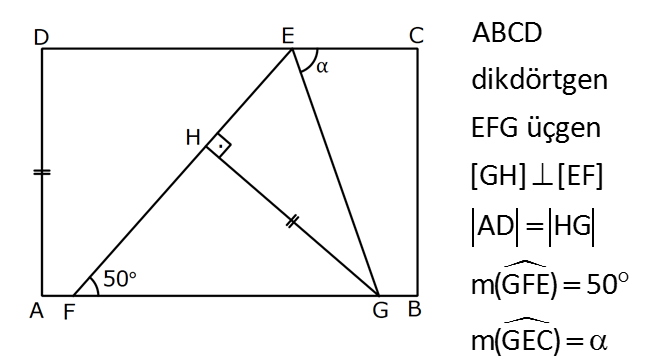
2.SORU
| | | | | |
Çözüm için Tıklayınız.
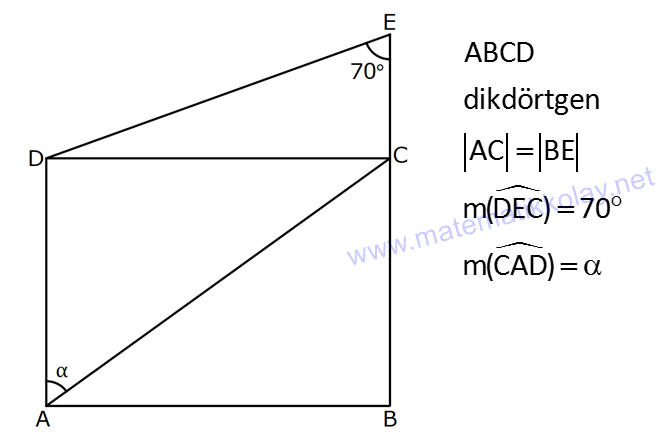
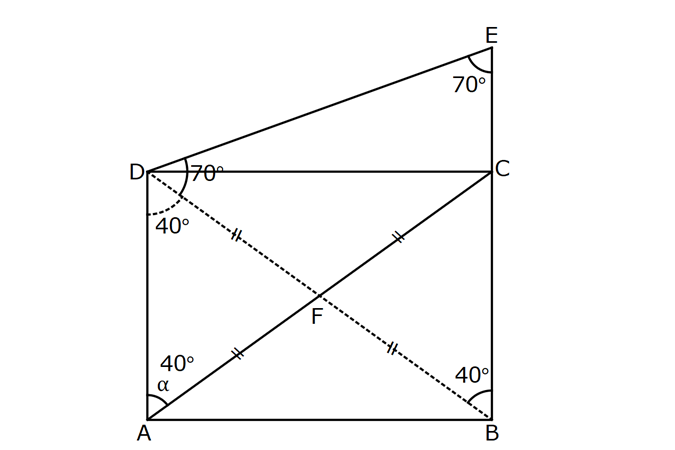
3.SORU
| | | | | |
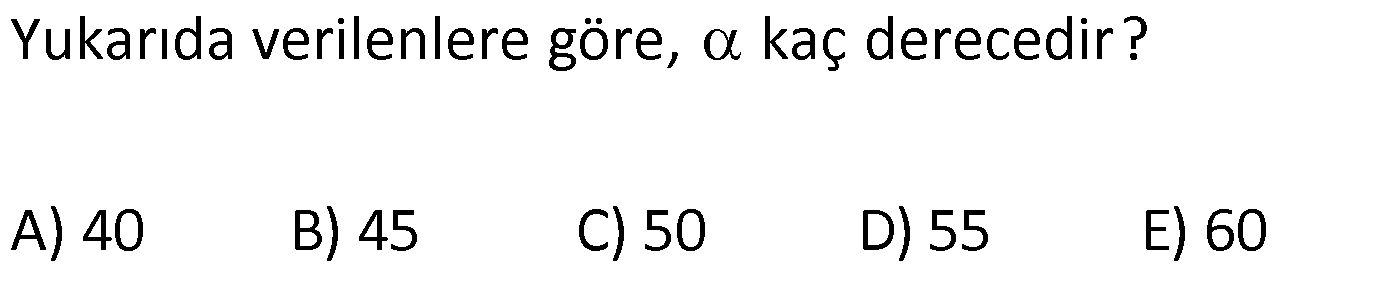
Çözüm için Tıklayınız.
4.SORU
| | | | | |
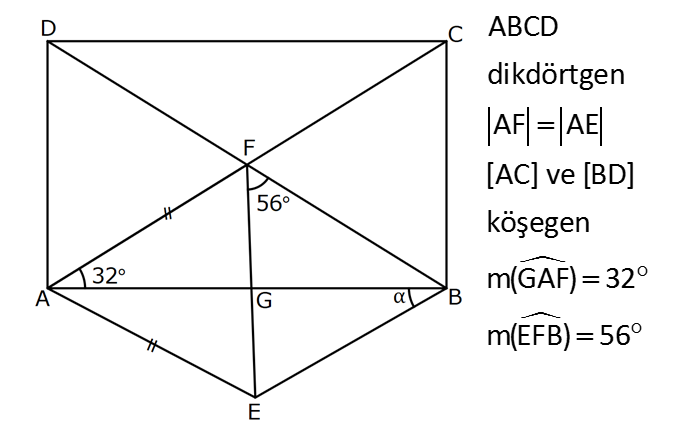
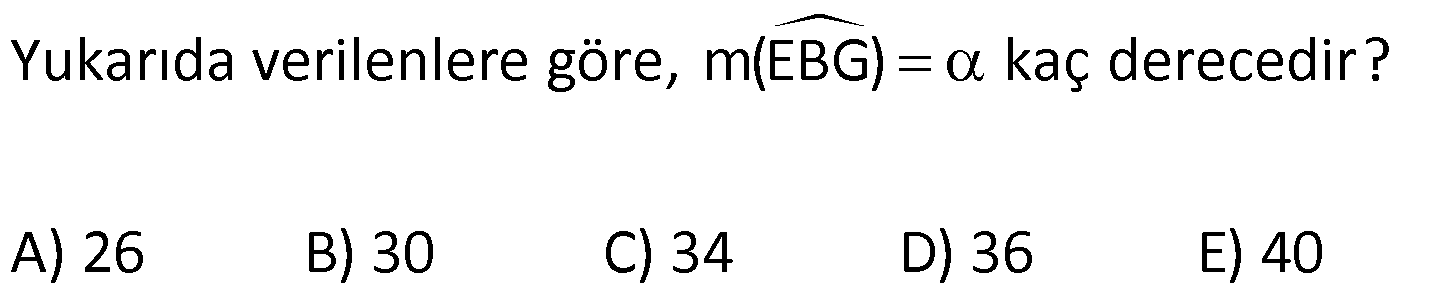
Çözüm için Tıklayınız.
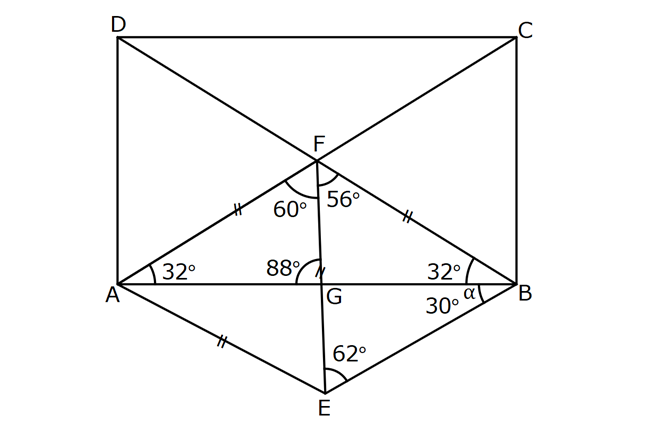
5.SORU
| | | | | |
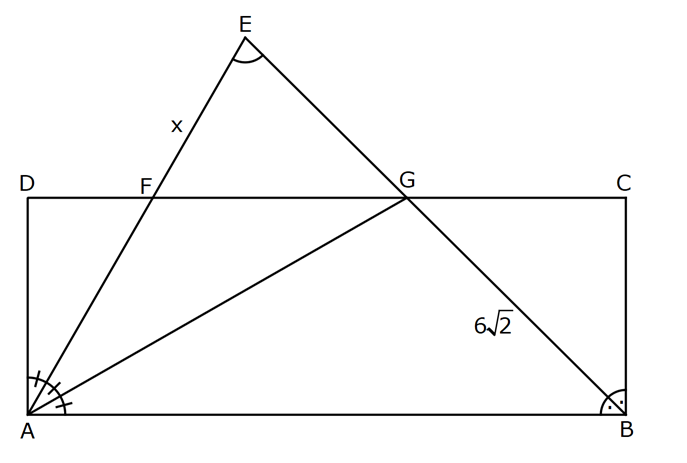
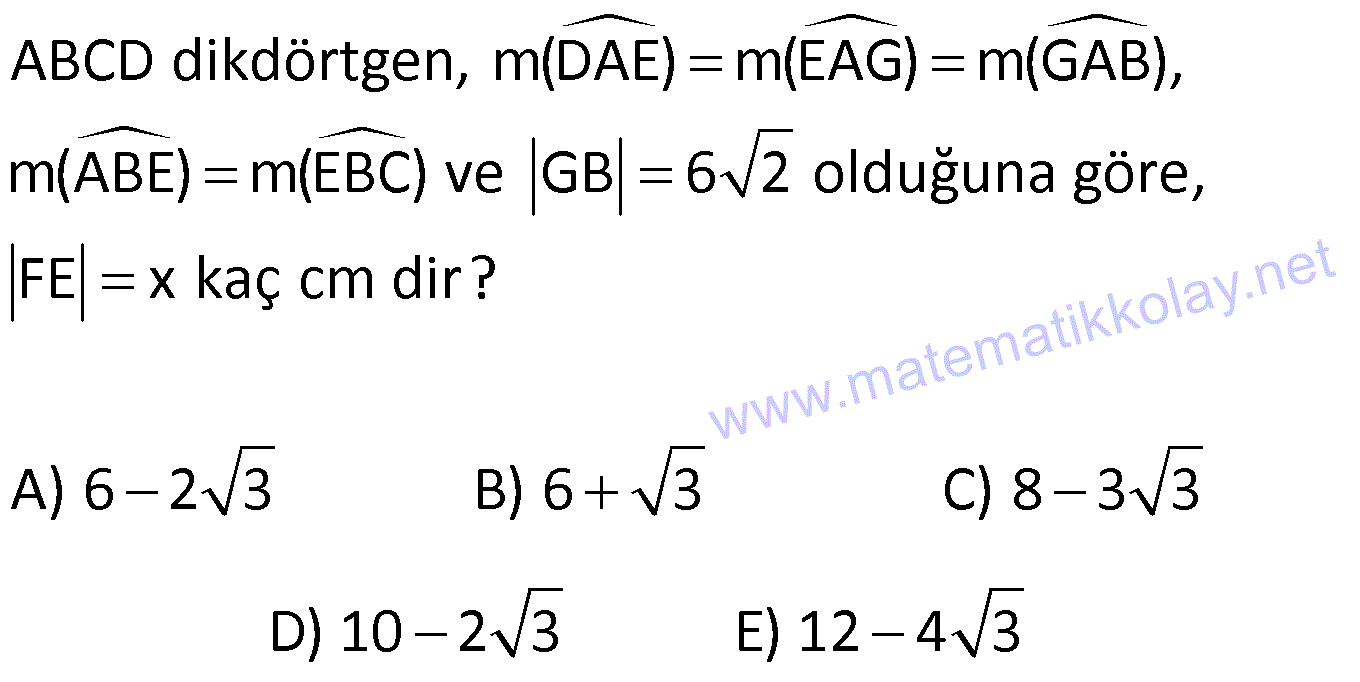
Çözüm için Tıklayınız.
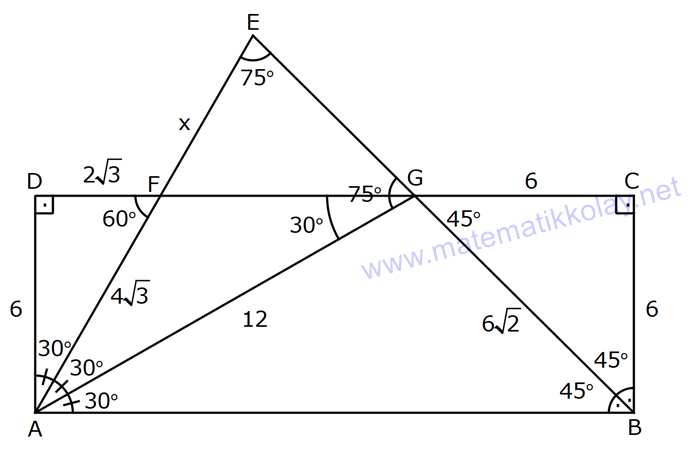
6.SORU
| | | | | |
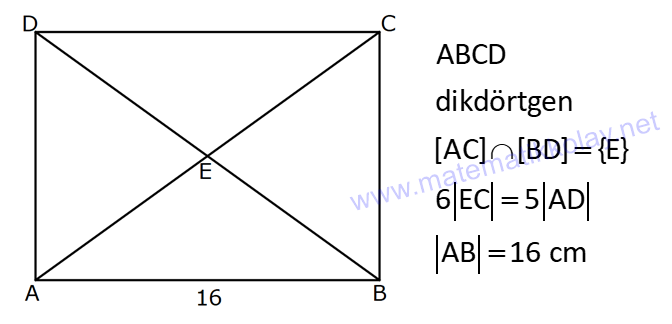
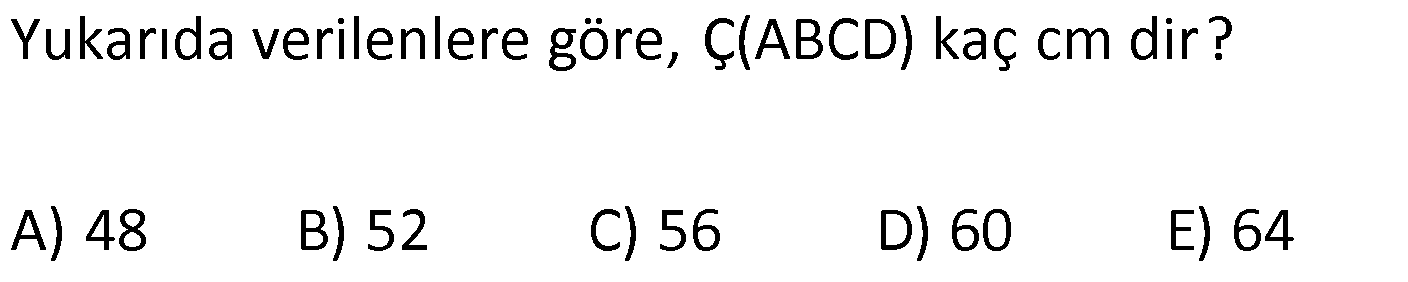
Çözüm için Tıklayınız.
7.SORU
| | | | | |
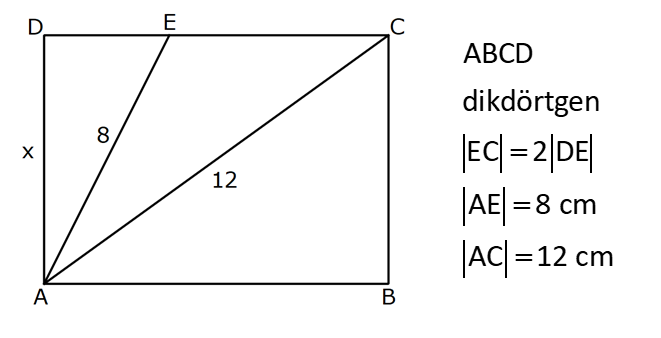
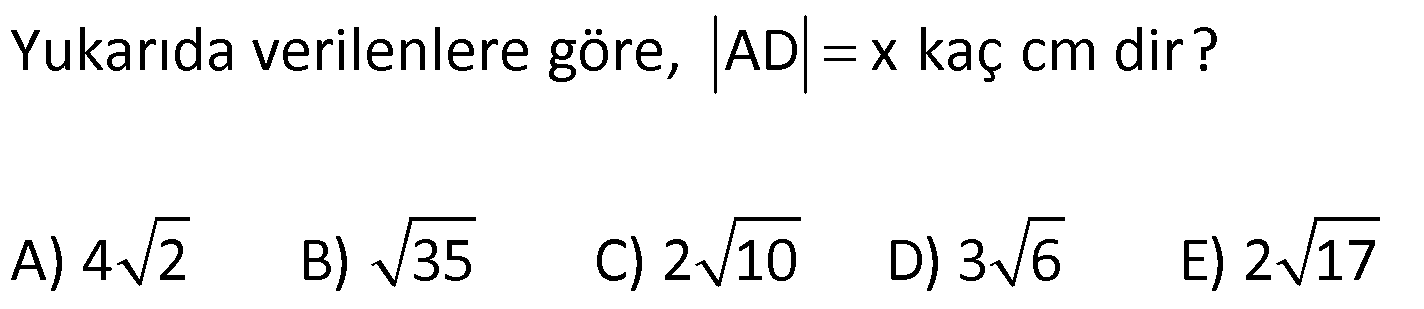
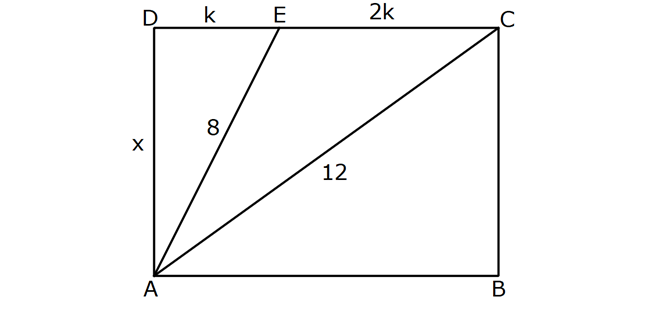
Çözüm için Tıklayınız.
8.SORU
| | | | | |
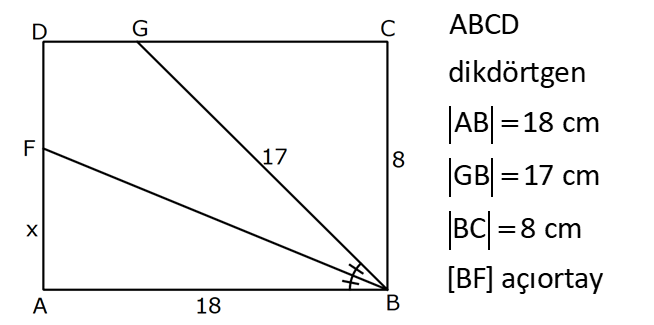
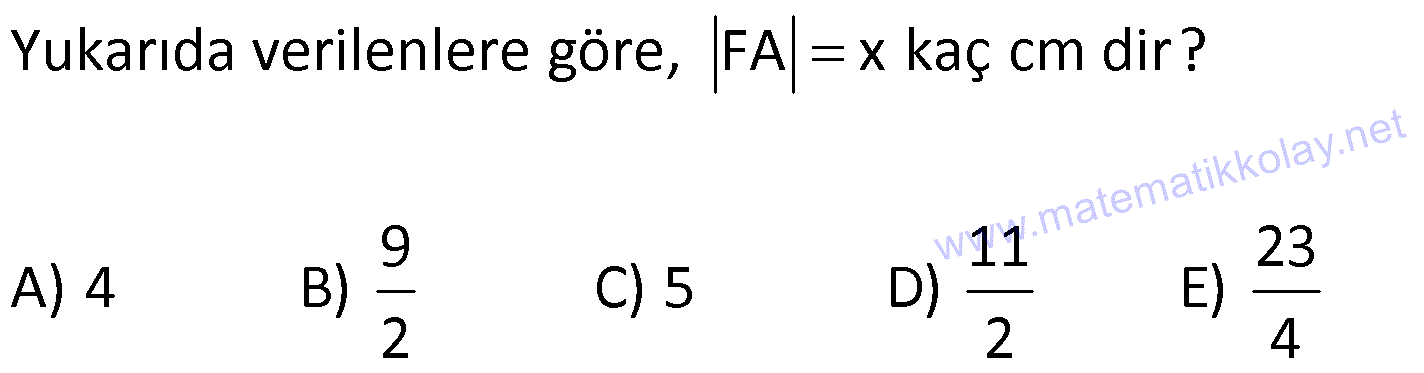
Çözüm için Tıklayınız.
9.SORU
| | | | | |
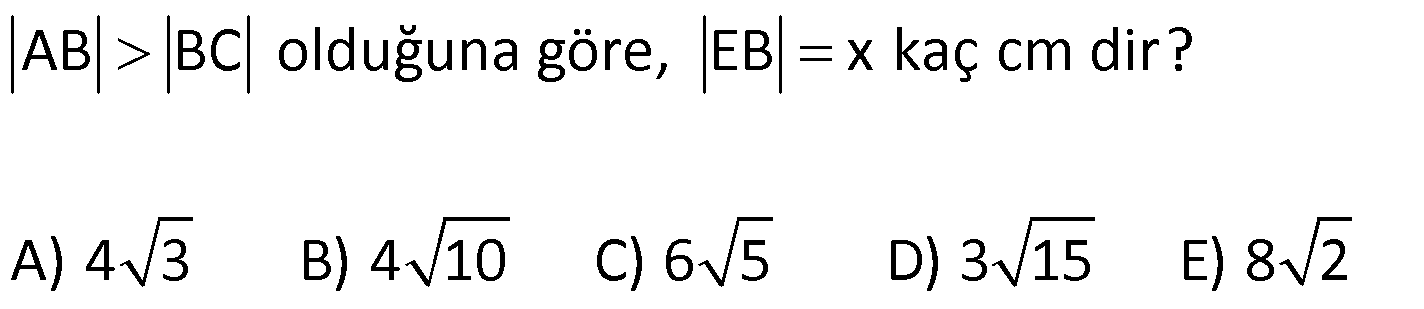
Çözüm için Tıklayınız.
10.SORU
| | | | | |
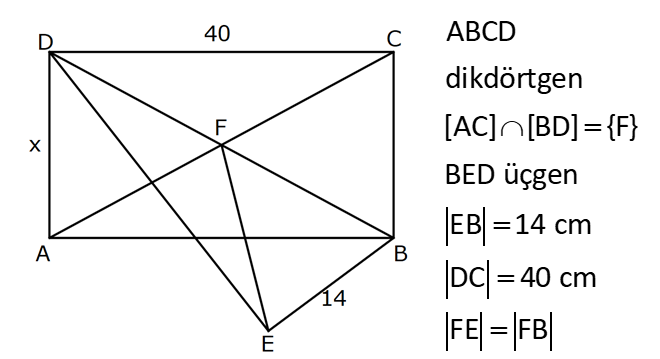
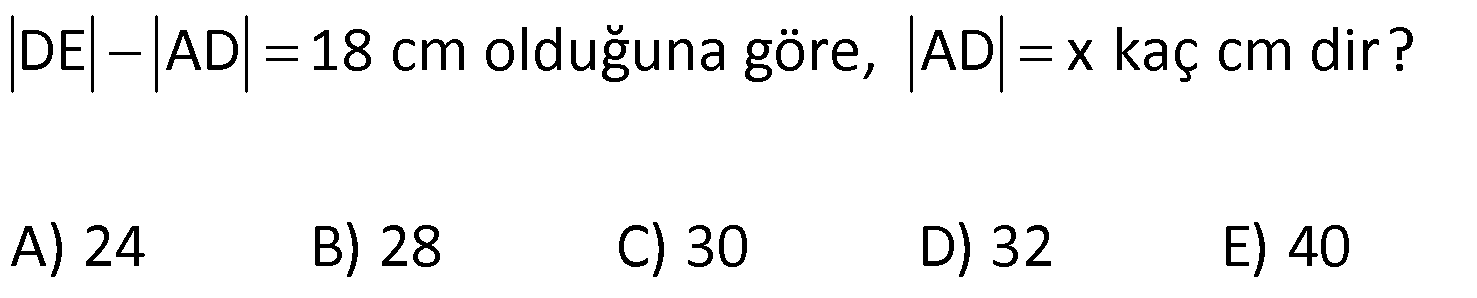
Çözüm için Tıklayınız.
Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
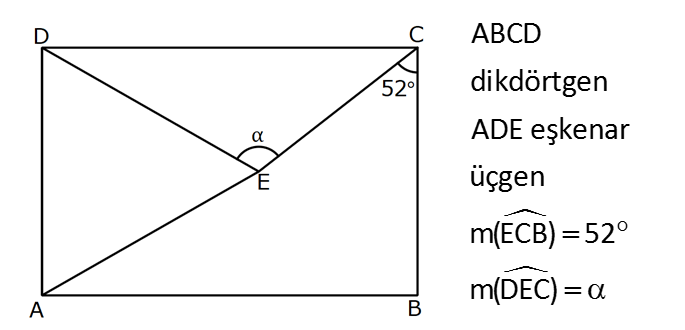
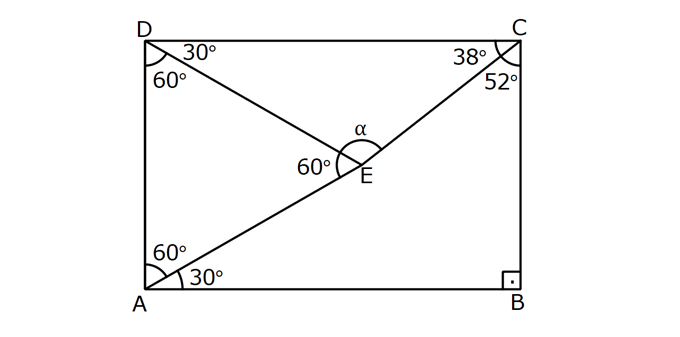
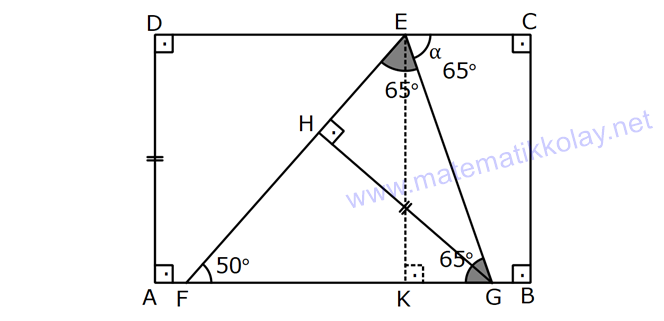
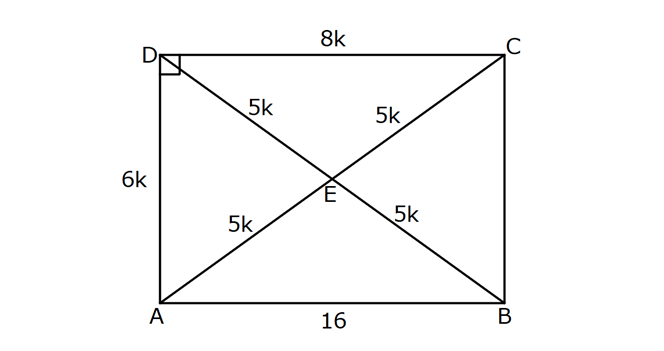
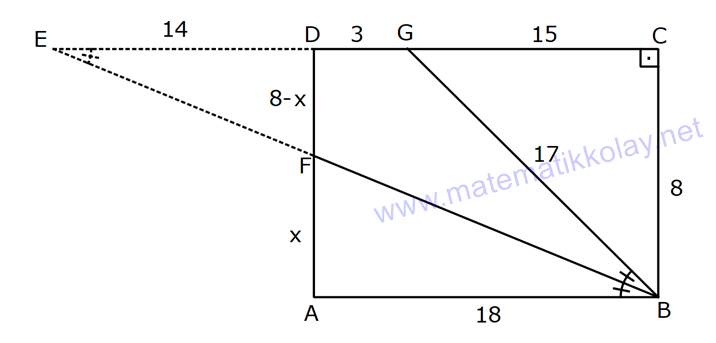
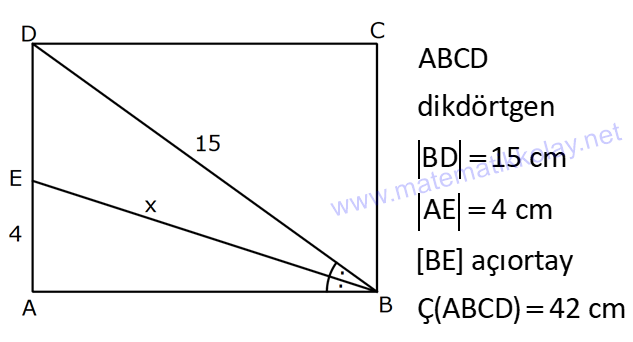
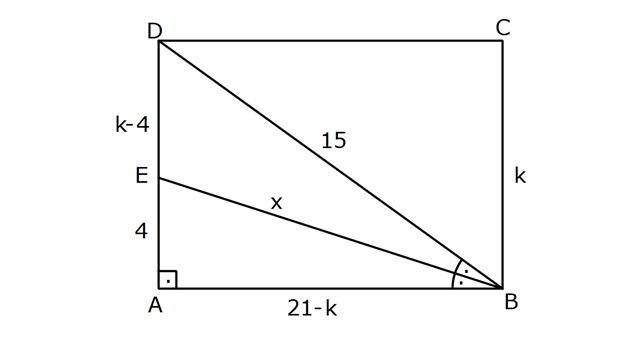
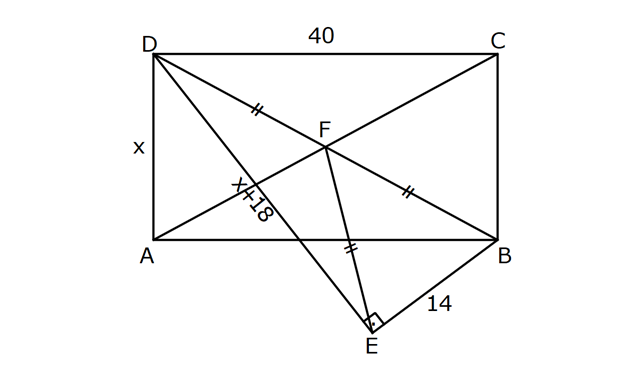
DİKDÖRTGENDE AÇI UZUNLUK www.matematikkolay.net 1) ABCD dikdörtgen ADE eşkenar üçgen m(ECB) 52 m(DEC) Yukarıda verilenlere göre, kaç derecedir ? A) 98 B) 102 C) 112 D) 118 E) 122 ÇÖZÜM: Tüm iç açıları dik açı olan dörtgene denir. Buna göre, m(ECD) 90 52 38 dir. ADE üçgeni eşkenar üçgen olduğundan, tüm iç açıları 60 dir. m(EDC) 90 60 30 Not: dikdörtgen kalır. DEC üçgeninin iç açıları toplamından, 30 38 180 68 180 112 dir. Cevap : C 2) ABCD dikdörtgen EFG üçgen [GH] [EF] AD HG m(GFE) 50 m(GEC) Yukarıda verilenlere göre, kaç derecedir ? A) 60 B) 65 C) 68 D) 70 E) 75 ÇÖZÜM: Dikdörtgenler, paralelkenarlara ait tüm özellikleri taşır. [EK] yüksekliğini çizersek, bu uzunluk AD ye eşit olur. EFG üçgeninde EK ve GH yükseklikleri eşit olmuş olur. Bu sebeple EFG üçgeni ikizkenar Not: dır. Yani, m(FGE) m(GEF) tir. 180 50 130 lik açıyı eşit paylaşırlar. 130 65 olurlar. 2 m(FGE) 65 ise, 65 dir (iç ters açı) . Cevap :B 3) www.matematikkolay.net ABCD dikdörtgen AC BE m(DEC) 70 m(CAD) Yukarıda verilenlere göre, kaç derecedir ? A) 40 B) 45 C) 50 D) 55 E) 60 ÇÖZÜM: Dikdörtgenin köşegenleri birbirine eşittir. Bu sebeple birbirini ortaladıkları parçalar, birbirine eşittir. Buna göre, [BD] yi çizersek BDE ikizkenar üçgenini elde ederiz. m(BDE) 70 olur. m(DBE) 180 Not: 70 70 40 olur. m(BDA) 40 dir (iç ters açı). DF AF olduğu için de 40 olur. Cevap : A 4) ABCD dikdörtgen AF AE [AC] ve [BD] köşegen m(GAF) 32 m(EFB) 56 Yukarıda verilenlere göre, m(EBG) kaç derecedir? A) 26 B) 30 C) 34 D) 36 E) 40 ÇÖZÜM: Dikdörtgende köşegen uzunlukları birbirine eşittir. Bu sebeple FB AF dir. m(ABF) 32 olur. AFB üçgeninin iç açıları toplamından, m(AFB) 180 32 32 116 dir. m(AFE) 116 56 60 kalır. AFE üçgeni ikizkena r üçgendi. Bir iç açısı da 60 ise, bu üçgen bir eşkenar üçgendir. FE uzunluğu da bu uzunluklara eşit olur. O halde, FEB üçgeni ikizkenar bir üçgendir. 180 56 124 İkiz açıları 62 dir. 2 2 62 32 30 o lur. Cevap : B 5) www.matematikkolay.net ABCD dikdörtgen, m(DAE) m(EAG) m(GAB), m(ABE) m(EBC) ve GB 6 2 olduğuna göre, FE x kaç cm dir? A) 6 2 3 B) 6 3 C) 8 3 3 D) 10 2 3 E) 12 4 3 ÇÖZÜM: 3 [BE] açıortayı 90 yi 45 ve 45 olarak böler. BCG üçgeni 45- 45- 90 üçgeni olur. BC 6 cm dir. AD 6 cm olur. 90 A noktasındaki 3 eşit açı da 30 olur. 3 ADF üçgeni 30 – 60 – 90 üçgeni olur. 6 DF 3 60 45 6 3 2 3 cm dir. 3 AF 2.2 3 4 3 cm olur. ADG üçgeni de 30 – 60 – 90 üçgenidir. AG 2.6 12 cm olur. ABE üçgeninin iç açıları toplamından m(AEB) m(EAB) m(ABE) 180 m(AEB) 105 180 m(AEB) 75 dir. AEG üçgen in iç açıları toplamından, 30 75 m(AGE) 180 m(AGE) 75 dir. O halde, AEG üçgeni ikizkenar üçgen olup, AE 12 cm dir. x 12 4 3 cm olur. Cevap : E 6) ABCD dikdörtgen [AC] [BD] {E} 6 EC 5 AD AB 16 cm Yukarıda verilenlere göre, Ç(ABCD) kaç cm dir? A) 48 B) 52 C) 56 D) 60 E) 64 ÇÖZÜM: www.matematikkolay.net 5k 6k 6 EC 5 AD Dikdörtgenin köşegenleri birbirine eşit olacağı için, birbirlerini ortaladıkları parçalar da birbirine eşittir. AE EC ED EB 5k dır. O halde, ACD üçgeni bir 6k – 8k -10k üçgenidir. 8k 16 cm ise k 2 2 cm dir. Ç(ABCD) 2(6k 8k) 28k 56 cm dir. Cevap: C 7) ABCD dikdörtgen EC 2 DE AE 8 cm AC 12 cm Yukarıda verilenlere göre, AD x kaç cm dir ? A) 4 2 B) 35 C) 2 10 D) 3 6 E) 2 17 ÇÖZÜM: 2k k 2 2 2 2 2 EC 2 DE ADC üçgeninde pisagor yaparsak x 9k 144 olur. ADE üçgeninde pisagor yaparsak _ x k 64 olur. Taraf tarafa çıkarırsak 8k 80 2 2 2 2 10 k 10 olur. x k 64 x 54 x 54 6.9 3 6 cm dir. Cevap : D 8) ABCD dikdörtgen AB 18 cm GB 17 cm BC 8 cm [BF] açıortay Yukarıda verilenlere göre, FA x kaç cm dir ? 9 11 23 A) 4 B) C) 5 D) E) 2 2 4 ÇÖZÜM: www.matematikkolay.net BCG üçgeni 8 15 17 üçgenidir. DG 18 15 3 cm kalır. [BF] ve [CD] doğrularını uzatarak, şekildeki gibi E noktasında birleştirelim. m(BED) m(ABF) olur. Açıortaydan dolayı EGB üçgeni ikizkenar üçgen olur. EG 1 7 cm dir. ED 17 3 14 cm kalır. [EC] // [AB] olduğundan, EDF üçgeni ile BAF üçgeni arasında kelebek benzerliği yapabiliriz. 18 9 14 7 x 8 x 72 9x 7x 72 9 16 2 x 9 x tir. Cevap: B 2 9) ABCD dikdörtgen BD 15 cm AE 4 cm [BE] açıortay Ç(ABCD) 42 cm AB BC olduğuna göre, EB x kaç cm dir? A) 4 3 B) 4 10 C) 6 5 D) 3 15 E) 8 2 ÇÖZÜM: 2 2 2 ( 9)( 16) Çevrenin yarısı 21 cm dir. Dikdörtgenin kısa kenarına k diyelim. Uzun kenarı 21 k olur. DE k 4 cm olur. Açıortay kuralını uygularsak, 15 21 k 60 21k 84 k 4k k 4 4 60 k 84 25k k 25k 144 0 (k 9)(k 2 2 2 2 2 16) 0 k 9 dur AB BC olduğu için . AB 21 9 12 cm dir. EAB üçgeninde pisagor yaparsak, x 4 12 x 16 144 x 160 x 160 16.10 4 10 cm dir. Cevap : B 10) ABCD dikdörtgen [AC] [BD] {F} BED üçgen EB 14 cm DC 40 cm FE FB DE AD 18 cm olduğuna göre, AD x kaç cm dir? A) 24 B) 28 C) 30 D) 32 E) 40 ÇÖZÜM: www.matematikkolay.net Köşegenler birbirini eşit böldükleri için, DEB üçgeninin içinde muhteşem üçlü oluşmuştur. Bu sebeple BED üçgeni bir dik üçgendir. BED üçgeninin hipotenüsü, dikdörtgenin bir köşe – genidir. ADC üçgeninin 2 2 2 2 2 de hipotenüsü dikdörtgenin köşe – genidir. İkisini birbirine eşitleyelim. x 40 (x 18) 14 x 2 1600 x 36x 324 196 1600 36x 520 1080 36x x 30 cm buluruz. Cevap : C
